Local heating realization by reverse thermal cloak

ABSTRACT Transformation thermodynamics, as one of the important branches among the extensions of transformation optics, has attracted plentiful attentions and interests recently. The result

of transformation thermodynamics, or called as “thermal cloak”, can realize isothermal region and hide objects from heat. In this paper, we presented the concept of “reverse thermal cloak”

to correspond to the thermal cloak and made a simple engineering definition to identify them. By full-wave simulations, we verified that the reverse thermal cloak can concentrate heat and

realize local heating. The performance of local heating depends on the anisotropic dispersion of the cloaking layer's thermal conductivity. Three-dimensional finite element simulations

demonstrated that the reverse thermal cloak can be used to heat up objects. Besides pre-engineered metamaterials, such reverse thermal cloak can even be realized with homogenous materials by

alternating spoke-like structure or Hashin coated-sphere structure. SIMILAR CONTENT BEING VIEWED BY OTHERS NONRECIPROCAL THERMAL PHOTONICS Article 10 April 2024 FLEXIBLE AND HIGH PRECISION

THERMAL METASURFACE Article Open access 01 September 2021 ROBUSTLY PRINTABLE FREEFORM THERMAL METAMATERIALS Article Open access 10 December 2021 INTRODUCTION With the born of transformation

optics in 20061,2, it grows prosperously with a lot of attention and has turned into a subject of great interest since it not only provides a general method in coordinate transformation but

also provides an effective design tool for manipulating electromagnetic wave3. In the past few years, transformation optics has been well developed beyond the domain of electromagnetic wave

to plentiful extensions in other fields, including acoustic wave4,5, liquid wave6, matter wave7 and elastic wave8,9, etc. The results of these transformations, or called as cloaks, can be

realized by pre-engineered metamaterials or even homogeneous natural materials with special-designed structures. One common type of cloaks is the core-shell structure, which maps a

concealment region into a surrounding shell region with inhomogeneous distribution of constitutive parameters10,11,12. The core-shell structure, like the typical Hashin coated sphere

structure, was initiatively described by Hashin9,13 as a model of composite comprised of spherical grains of one phase embedded in a matrix of another phase. Hashin pointed out how to design

the phase materials and the corresponding fractions so that inserting the coated sphere into the matrix would not disturb the uniform electromagnetic field outside14. Analogy to

transformation optics, Guenneau _et al._15 first extended the transformation methodology to the area of thermodynamics and proposed the concept of thermal cloak to channel the heat flow to

realize a local isothermal region where the temperature gradient vanishes. Further studies16,17,18,19 demonstrated that thermal cloak can be realized with homogenous and finite thermal

conductivity by simulations and experiments. More specifically, Han et al.16 presented that thermal cloak can be realized by isotropic natural materials; Schittny et al.17 designed and

manufactured a thermal cloak comprised of copper rings interlaid with plastic. From the view of guiding heat flux, Narayana and Sato18 did excellent and systematic work about controlling the

heat flow by the engineering materials. By shielding, concentrating and inverting the heat current, they experimentally showed that artificially engineered thermal materials can yield

characteristics that go far beyond the conventional media. The concept of thermal cloak, in fact, is derived from the optical invisible cloak and it is aimed at hiding object from heat or

rendering heat invisible in certain region. The thermal cloak can be achieved by anisotropic thermal conductivity distribution where the azimuthal component is much larger than the radial

component (>). Inspired by the previous work, one possible idea turns up that could we apply the thermal cloak reversely (>) and realize a local heating region where the temperature

gradient is large enough to heat up objects? By utilizing the transformation thermodynamics and tailoring the dispersion of thermal conductivity, here we demonstrated that the reverse

application of thermal cloak can efficiently realize a local heating region where the temperature gradient is more considerable than that of the outside region. Steady full-wave simulations

show that the temperature profile in the central region strongly depends on the anisotropy of thermal conductivity. Transient simulations illustrate that heat diffuses faster in the left

part of the reverse thermal cloak and slower in the right part, thus large temperature gradient is formed in the central region. By modeling a substrate consisting of reverse thermal cloak

and assembling a cubic probe onto the central region, the corresponding temperature fields on the cubic probe show that local heating effect was enhanced with reverse thermal cloak. Two

possible methods were also presented to realize such reverse thermal cloak. RESULTS With transformation thermodynamics, we derived that the radial thermal conductivity and the azimuthal

thermal conductivity are the inverse of each other, as shown in Eq. (1). By defining , where _C_ is a constant, a cloak can be realized with constant thermal conductivity. For thermal

cloaks, the constant _C_ is usually less than 116, implying the radial conductivity is much smaller than the azimuthal conductivity . The performance characteristics of thermal cloak are

totally attributed to its anisotropic distribution of thermal conductivity. In this paper, we proposed the concept of “reverse thermal cloak” where is much larger than , i.e. the constant

_C_ is larger than 1. With full-wave simulations based on finite element method (FEM), the steady-state performances of the cloaks were examined. The large commercial software package COMSOL

Multiphysics was used to conduct the simulations. For comparison, a homogeneous plane with constant thermal conductivity was also simulated. In the simulations, the left and right

boundaries were kept at constant temperature, i.e. 400 K and 300 K, respectively. The top and bottom boundaries are thermally insulated. The interior and exterior radii of the annular

thermal cloak (reverse thermal cloak) are 1 cm and 2 cm, respectively. The dimensions of the whole domain are 10×10 cm2. The thermal conductivities of the core region and the substrate are

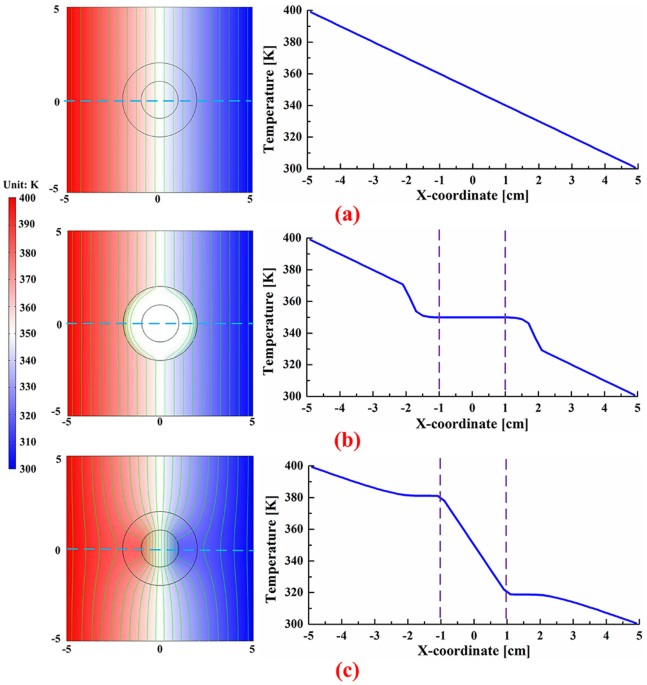
kept as 0.1 W/(m·K) and 1.0 W/(m·K), respectively. Fig. 1 shows the temperature profiles and corresponding temperature curves of the section lines on a homogenous plane, a thermal cloak and

a reverse thermal cloak, respectively. From Fig. 1(a), the temperature profile of the homogenous plane is uniform and the temperature gradient is constant throughout the plane. From Fig.

1(b), the temperature profiles outside the thermal cloak are all the same with Fig. 1(a), but the heat tends to be away from the inner core region and travels close to the outside edge of

the thermal cloak (_C_ = = 0.1 W/(m·K), = 10 W/(m·K)). From both the temperature contour and the temperature gradient of the section line, we can see that thermal cloak can realize an

isothermal region in the central domain. This implies that any object placed in the interior region appears to be concealed since the outside heat flow looks like as if there is no

disturbance at all in the central region (the temperature gradient outside the thermal cloak is the same with that in Fig. 1(a)). This is the reason and origin of the definition of “thermal

cloak”. Fig. 1(c) shows that temperature field of the reverse thermal cloak in which we adjust the constant _C_ to 10 (_C_ = = 10 W/(m·K), = 0.1 W/(m·K)). We can see that the temperature

profiles bend toward the central region and the temperature gradient in the central region is enhanced greatly. More vivid comparison between the thermal cloak and the reverse thermal cloak

can be found in Fig. 2. The reverse thermal cloak tends to concentrate the heat and have the most heat diffuse from it, resulting in local heating and large temperature gradient. Isothermal

region forms in the thermal cloak while a sharp temperature drop arises in the reverse thermal cloak. To further demonstrate the local heating phenomenon, we plotted the temperature curves

on the cut plane (x = −0.5 cm) in Fig. 3. Obvious local high temperature can be observed in the central region. We can also see that when the constant _C_ increases from 5 to 20, the local

temperature in the central region is enhanced. The larger the constant C is, the larger the thermal conductivity anisotropy is. The trend in Fig. 3 implies that large anisotropy of the

thermal conductivity distribution leads to enhanced local heating effect. Transient simulations of the reverse thermal cloak were carried out and the heat diffusion processes are shown in

Fig. 4 (_C_ = = 10 W/(m·K), = 0.1 W/(m·K)). In the beginning, heat has not conducted to the right part yet and the isotherms squeeze in the left part. With time elapse, heat conducts to the

right part gradually and the isotherms stretch to the whole domain. At _t_ = 60 second, the thermal system almost get its equilibrium state and the corresponding isotherms are symmetric in

the left and right parts. No matter in the transient state (see Fig. 4) or in the steady state (see Fig. 1 and Fig. 2), we can discover that the isotherms bend toward the central region in

both the left and right parts. This implied that in the reverse thermal cloak, heat conducts faster in the left part and slower in the right part. As a result, compact isotherms and large

temperature gradient form in the central region. From above analyses, we can observe the local heating effect and there exists a large temperature gradient in the central region of the

reverse thermal cloak. Since the driving force of heat diffuse is the temperature gradient, one idea is that we could utilize the large temperature gradient to heat up objects. To verify our

idea, we built a three-dimensional model in which we modeled a substrate consisting of a reverse thermal cloak (_C_ = = 10 W/(m·K), = 0.1 W/(m·K)) and then mounted a cubic probe on the

central region, as shown in Fig. 5(a). The dimensions of the substrate are 10×10×0.5 cm3. The dimensions of the cubic probe are 1×1×0.5 cm3. The interior and exterior radii of the annular

reverse thermal cloak are 1 cm and 2 cm, respectively. For comparison, we also built the same-dimensional model except that the substrate is a homogeneous plane without reverse thermal

cloak. After steady-state simulations, we selected the temperature contours on the front surface of the cubic probe (on the plane of x = −0.5 cm) to demonstrate our idea. The temperature

comparisons are shown in Fig. 5(b) and Fig. 5(c). We can see that the maximum temperature of the cubic probe is 370 K when the substrate is with a reverse thermal cloak; the maximum

temperature is 357 K when the substrate is without a reverse thermal cloak. Thus the reverse thermal cloak can be utilized to heat up objects. To realize such a reverse thermal cloak whose

radial thermal conductivity is smaller than its azimuthal thermal conductivity, we designed a composite structure made by alternating spoke-like layers of two homogeneous materials. As shown

in Fig. 6, the structure consists of two isotropic materials, i.e. material A and material B. The thermal conductivities of these two materials are 10 W/(m·K) and 0.1 W/(m·K), respectively.

All the boundary conditions are kept the same. The simulated temperature profile is similar to above simulations where compact isotherms and local heating effect form in the central region.

This implies that the reverse thermal cloak not only can be realized by pre-engineered metamaterials, but also can be realized by homogeneous materials with alternating spoke-like

structures. Another method to realize such kind of reverse thermal cloak with homogeneous materials can ascend to the Hashin coated sphere. According to the two-dimensional Hashin-Shtrikman

formula14, the effective thermal conductivity can be calculated as With where , are the thermal conductivities of the core region and the shell region, respectively. _f__1_ and _f__2_ are

the two-dimensional volume fraction, _r__1_ and _r__2_ are the exterior radii of the circular core and the cloaking shell. When equals to the thermal conductivity of the outside matrix ,

reverse thermal cloak can be realized. According to dimensions and thermal conductivities mentioned above, the thermal conductivity of the cloaking shell can be calculated as 0.918 W/(m·K)

in this paper. With the same method, we simulated the temperature field and the result was plotted in Fig. 7. It is seen that the green isotherms and the white streamlines are orthometric to

each other in panel. The isotherms bend to the core region and a large temperature gradient forms there. Therefore, with the Hashin-Shtrikman formula, we can design the dimensions and

thermal conductivities to realize reverse thermal cloaks. But when comparing Fig. 7 with Fig. 4 and Fig. 6, it is also seen that the thermal gradient in Hashin coated sphere is not as

compact as that realized by pre-engineered metamaterials, nor homogeneous materials with alternating spoke-like structures. Thus it is perceived that the local heating effect in Hashin

coated sphere is not as strong as the other two and the heat-concentration ability of Hashin coated sphere is also limited. DISCUSSION In summary, we demonstrated in this study that reverse

thermal cloak can be applied to realize local heating. Unlike the thermal cloak can realize isothermal region and render heat invisible from the outside temperature field, the reverse

thermal cloak can bend the isotherms to the central region and realize large temperature gradient there. Due to the large temperature gradient, local heating phenomenon was observed. Such

“local heating” phenomenon can be enhanced by re-distributing the dispersion of thermal conductivity in the domain of the reverse thermal cloak. Here, a way to realize local heating was

proposed by the reverse thermal cloak. Like the fabrication of thermal cloak, the reverse thermal cloak can also be fabricated with pre-engineered metamaterial or even with homogenous

materials by spoke-like structures or Hashin coated-sphere structure. With the reverse thermal cloak, we can realize the local heating in many fields. For instance, in the electronic

packaging, with local heating, we may avoid heating some temperature-sensitive components or causing printed circuit board (PCB) warping. It should be pointed out that the reverse thermal

cloak was proposed to correspond to the thermal cloak during the research of thermal cloak. In this paper, we simply defined the difference between these two cloaks as that: for thermal

cloak, the constant _C_ ( = radial thermal conductivity ) is less than 1; for the reverse thermal cloak, the constant _C_ is larger than 1. The essence of both thermal cloak and reverse

thermal cloak is the anisotropic dispersion of thermal conductivity. When compared with the thermal concentrator15,18, the present reverse thermal cloak exhibits similar characteristics but

in a much simpler engineering way. The thermal concentrator has specific formula to identify the dispersion of thermal conductivity15, while in this paper we extended the limitation of

thermal conductivity and gave a general formula in Eq. (1). Moreover, we paid more attentions to the application of reverse thermal cloak, rather than just staying in the theoretical or

laboratory stages. What should be emphasized is that the present reverse thermal cloak can also be applied to other shape cloaks, like square, rectangular, elliptic, etc. METHODS When a

temperature gradient exists in a body, experience has shown that there is an energy transfer from the high-temperature region to the low-temperature region. For a steady state without heat

source, the control equation can be written as , where is the thermal conductivity and is the temperature. Similar to the invariance of Maxwell equations in the transformation optics,

Guenneau _et al._15 pointed out that the heat conduction equations can also be written in a form-invariant manner under coordinate transformations. Thus, in the transformed space, the heat

conduction equation can be re-written as With where is the Jacobian matrix with components defined as . The Jacobian matrix characterizes the geometrical variation in the original space and

the transformed space . Eqs. (2) and (3) construct the basis of transformation thermodynamics and we can design and manipulate the flow of heat by an arbitrary coordinate transformation. One

seminal typical design of thermal cloak was consulted to the invisible cloak proposed by Pendry _et al_.1,10 With the simple coordinate transformation in Eq. (4), we can squeeze the heat

flow from a central region () in the original space into a shell region () in the transformed space , while the rest of heat flow (in the region ) are maintained. where _R__1_ and _R__2_ are

the interior and exterior radii of the annular thermal cloak. Substituting Eq. (6) into Eqs. (4) and (5) yields Eq. (1). REFERENCES * Pendry, J. B., Schurig, D. & Smith, D. R.

Controlling electromagnetic fields. Science 312, 1780–1782 (2006). Article  CAS  ADS  MathSciNet  Google Scholar  * Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).

Article  CAS  ADS  MathSciNet  Google Scholar  * Zolla, F., Guenneau, S., Nicolet, A. & Pendry, J. B. Electromagnetic analysis of cylindrical invisibility cloaks and the mirage effect.

Opt. Lett. 32, 1069–1071 (2007). Article  ADS  Google Scholar  * Zhang, S., Xia, C. G. & Fang, N. Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301 (2011).

Article  ADS  Google Scholar  * Zhu, J. et al. Acoustic rainbow trapping. Sci. Rep. 3, 1728 (2013). Article  CAS  Google Scholar  * Farhat, M., Enoch, S., Guenneau, S. & Movchan, A. B.

Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 101, 134501 (2008). Article  CAS  ADS  Google Scholar  * Zhang, S., Genov, D. A., Sun, C. &

Zhang, X. Cloaking of matter waves. Phys. Rev. Lett. 100, 123002 (2008). Article  ADS  Google Scholar  * Brun, M., Guenneau, S. & Movchan, A. B. Achieving control of in-plane elastic

waves. Appl. Phys. Lett. 94, 061903 (2009). Article  ADS  Google Scholar  * Hashin, Z. The Elastic Moduli of Heterogeneous Materials. J. Appl. Mech. 29, 143–150 (1962). Article  CAS  ADS 

MathSciNet  Google Scholar  * Pendry, J. B., Aubry, A., Smith, D. R. & Maier, S. A. Transformation optics and subwavelength control of light. Science 337, 549–552 (2012). Article  CAS 

ADS  MathSciNet  Google Scholar  * Liu, Y. M. & Zhang, X. Recent advances in transformation optics. Nanoscale 4, 5277 (2012). Article  CAS  ADS  Google Scholar  * Kundtz, N. B., Smith,

D. R. & Pendry, J. B. Electromagnect design with transformation optics. Proc. IEEE 99, 1622–1633 (2011). Article  Google Scholar  * Hashin, Z. & Shtrikman, S. A Variational Approach

to the Theory of the Effective Magnetic Permeability of Multiphase Materials. J. Appl. Phys. 33(10), 3125–3131 (1962). Article  CAS  ADS  Google Scholar  * Milton, G. W. Assemblages of

spheres, ellipsoids and other neutral inclusions., The Theory of Composites 115–117 (Cambridge, New York, 2004). * Guenneau, S., Amra, C. & Veynante, D. Transformation thermodynamics:

cloaking and concentrating heat flux. Opt. Express 20, 8207–8218 (2012). Article  ADS  Google Scholar  * Han, T. C., Yuan, T., Li, B. W. & Qiu, C. W. Homogenous thermal cloak with

constant conductivity and tunable heat localization. Sci. Rep. 3, 1593 (2013). Article  CAS  ADS  Google Scholar  * Schittny, R., Kadic, M., Guenneau, S. & Wegener, M. Experiments on

transformation thermodynamics: molding the flow of heat. Phys. Rev. Lett. 110, 195901 (2013). Article  ADS  Google Scholar  * Narayana, S. & Sato, Y. Heat flux manipulation with

engineered thermal materials. Phys. Rev. Lett. 108, 214303 (2012). Article  ADS  Google Scholar  * Leonhardt, U. Cloaking of heat. Nature 498, 440–441 (2013). Article  CAS  ADS  Google

Scholar  Download references ACKNOWLEDGEMENTS The authors would like to acknowledge the financial support in part by Natural Science Foundation of China (51376070) and in part by 973 Project

of the Ministry of Science and Technology of China (2011CB013105) and in part by National 863 Project of the Ministry of Science and Technology of China (2011AA03A109). AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * State Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China Run Hu, Jinyan

Hu & Xiaobing Luo * School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan, 430074, China Xuli Wei Authors * Run Hu View author publications

You can also search for this author inPubMed Google Scholar * Xuli Wei View author publications You can also search for this author inPubMed Google Scholar * Jinyan Hu View author

publications You can also search for this author inPubMed Google Scholar * Xiaobing Luo View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS

R.H., X.L.W., J.Y.H. and X.B.L. contributed in the discussion. R.H. and J.Y.H. participated in the simulation. R.H. prepared the manuscript. R.H. and X.B.L. conceived the idea and revised

the manuscript. X.B.L. supervised the project. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed

under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Hu, R., Wei, X., Hu, J. _et al._ Local heating realization by reverse thermal cloak. _Sci Rep_ 4, 3600 (2014).

https://doi.org/10.1038/srep03600 Download citation * Received: 11 June 2013 * Accepted: 10 December 2013 * Published: 08 January 2014 * DOI: https://doi.org/10.1038/srep03600 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative