Fitting elephants in modern machine learning by statistically consistent interpolation

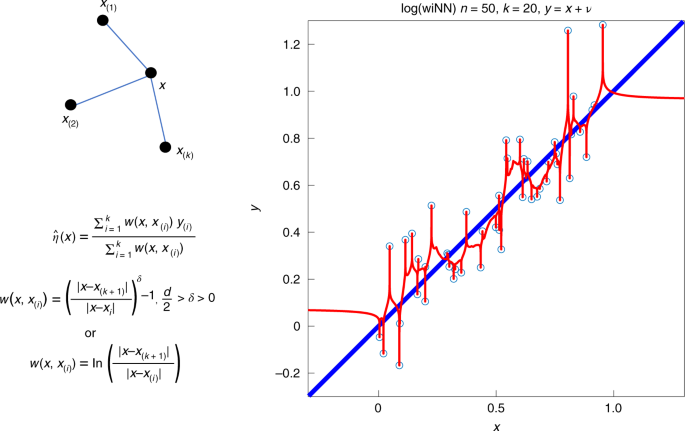
ABSTRACT Textbook wisdom advocates for smooth function fits and implies that interpolation of noisy data should lead to poor generalization. A related heuristic is that fitting parameters

should be fewer than measurements (Occam’s razor). Surprisingly, contemporary machine learning approaches, such as deep nets, generalize well, despite interpolating noisy data. This may be

understood via statistically consistent interpolation (SCI), that is, data interpolation techniques that generalize optimally for big data. Here, we elucidate SCI using the weighted

interpolating nearest neighbours algorithm, which adds singular weight functions to _k_ nearest neighbours. This shows that data interpolation can be a valid machine learning strategy for

big data. SCI clarifies the relation between two ways of modelling natural phenomena: the rationalist approach (strong priors) of theoretical physics with few parameters, and the empiricist

(weak priors) approach of modern machine learning with more parameters than data. SCI shows that the purely empirical approach can successfully predict. However, data interpolation does not

provide theoretical insights, and the training data requirements may be prohibitive. Complex animal brains are between these extremes, with many parameters, but modest training data, and

with prior structure encoded in species-specific mesoscale circuitry. Thus, modern machine learning provides a distinct epistemological approach that is different both from physical theories

and animal brains. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your institution

Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $29.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 12

digital issues and online access to articles $119.00 per year only $9.92 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices

may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support

SIMILAR CONTENT BEING VIEWED BY OTHERS PIECEWISE LINEAR NEURAL NETWORKS AND DEEP LEARNING Article 09 June 2022 SCALABLE SPATIOTEMPORAL PREDICTION WITH BAYESIAN NEURAL FIELDS Article Open

access 11 September 2024 A REVIEW OF SOME TECHNIQUES FOR INCLUSION OF DOMAIN-KNOWLEDGE INTO DEEP NEURAL NETWORKS Article Open access 20 January 2022 REFERENCES * Dyson, F. A meeting with

Enrico Fermi. _Nature_ 427, 297 (2004). Article  Google Scholar  * James, G., Witten, D., Hastie, T. & Tibshirani, R. _An Introduction to Statistical Learning_ Vol. 112 (Springer, 2013).

* Györfi, L., Kohler, M., Krzyzak, A. & Walk, H. _A Distribution-Free Theory of Nonparametric Regression_ (Springer, 2002). * Zhang, C., Bengio, S., Hardt, M., Recht, B. & Vinyals,

O. Understanding deep learning requires rethinking generalization. In _International Conference on Learning Representations_ (ICLR, 2017). * Wyner, A. J., Olson, M., Bleich, J. & Mease,

D. Explaining the success of adaboost and random forests as interpolating classifiers. _J. Mach. Learn. Res._ 18, 1–33 (2017). MathSciNet  MATH  Google Scholar  * Belkin, M., Ma, S. &

Mandal, S. To understand deep learning we need to understand kernel learning. In _Proc. 35th International Conference on Machine Learning_ 541–549 (PMLR, 2018). * Belkin, M., Hsu, D. &

Mitra, P. Overfitting or perfect fitting? Risk bounds for classification and regression rules that interpolate. In _Advances in Neural Information Processing Systems_ Vol. 31 (NIPS, 2018). *

Cutler, A. & Zhao, G. Pert-perfect random tree ensembles. _Comput. Sci. Stat._ 33, 490–497 (2001). Google Scholar  * Donoho, D. L. & Tanner, J. Sparse nonnegative solution of

underdetermined linear equations by linear programming. _Proc. Natl Acad. Sci. USA_ 102, 9446–9451 (2005). Article  MathSciNet  Google Scholar  * Wainwright, M. J. _High-Dimensional

Statistics_: _A Non-Asymptotic Viewpoint_ Vol. 48 (Cambridge Univ. Press, 2019). * Rakhlin, A. & Zhai, X. Consistency of interpolation with laplace kernels is a high-dimensional

phenomenon. In _Proc. Thirty-Second Conference on Learning Theory_ 2595–2623 (PMLR, 2019). * Ongie, G., Willett, R., Soudry, D. & Srebro, N. A function space view of bounded norm

infinite width ReLU nets: the multivariate case. In _International Conference on Learning Representations_ (ICLR, 2020). * Belkin, M., Hsu, D., Ma, S. & Mandal, S. Reconciling modern

machine-learning practice and the classical bias–variance trade-off. _Proc. Natl Acad. Sci. USA_ 116, 15849–15854 (2019). Article  MathSciNet  Google Scholar  * Liang, T. & Rakhlin, A.

Just interpolate: kernel “ridgeless” regression can generalize. _Ann. Stat._ 48, 1329–1347 (2020). Article  MathSciNet  Google Scholar  * Bartlett, P. L., Long, P. M., Lugosi, G. &

Tsigler, A. Benign overfitting in linear regression. _Proc. Natl Acad. Sci. USA_ 117, 30063–30070 (2020). Article  Google Scholar  * Montanari, A., Ruan, F., Sohn, Y. & Yan, J. The

generalization error of max-margin linear classifiers: high-dimensional asymptotics in the overparametrized regime. Preprint at https://arxiv.org/pdf/1911.01544.pdf (2019). * Karzand, M.

& Nowak, R. D. Active learning in the overparameterized and interpolating regime. Preprint at https://arxiv.org/pdf/1905.12782.pdf (2019). * Xing, Y., Song, Q. & Cheng, G.

Statistical optimality of interpolated nearest neighbor algorithms. Preprint at https://arxiv.org/pdf/1810.02814.pdf (2018). * Anthony, M. & Bartlett, P. L. _Neural Network Learning_:

_Theoretical Foundations_ (Cambridge Univ. Press, 1999). * Arora, S., Du, S., Hu, W., Li, Z. & Wang, R. Fine-grained analysis of optimization and generalization for overparameterized

two-layer neural networks. In _International Conference on Machine Learnin_g 322–332 (PMLR, 2019). * Allen-Zhu, Z., Li, Y. & Liang, Y. Learning and generalization in overparameterized

neural networks, going beyond two layers. In _Advances in Neural Information Processing Systems_ Vol. 32, 6158–6169 (NIPS, 2019). * Schapire, R. E. et al. Boosting the margin: a new

explanation for the effectiveness of voting methods. _Ann. Stat._ 26, 1651–1686 (1998). MathSciNet  MATH  Google Scholar  * Mücke, N. & Steinwart, I. Global minima of DNNs: the plenty

pantry. Preprint at https://arxiv.org/pdf/1905.10686.pdf (2019). * Nadaraya, E. A. On estimating regression. _Theory Probability Appl._ 9, 141–142 (1964). Article  Google Scholar  * Watson,

G. Smooth regression analysis. _Sankhya A_ 26, 359–372 (1964). MathSciNet  MATH  Google Scholar  * Cover, T. & Hart, P. Nearest neighbor pattern classification. _IEEE Trans. Inf. Theory_

13, 21–27 (1967). Article  Google Scholar  * Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In _Proc. 23rd ACM National Conference_ 517–524 (ACM, 1968). *

Devroye, L., Györfi, L. & Krzyżak, A. The Hilbert kernel regression estimate. _J. Multivariate Anal._ 65, 209–227 (1998). Article  MathSciNet  Google Scholar  * Waring, E. VII. Problems

concerning interpolations. _Philos. Trans. R. Soc. Lond_ 69, 59–67 (1779). Google Scholar  * Runge, C. Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten. _Z.

Math. Phys._ 46, 20 (1901). MATH  Google Scholar  * Xing, Y., Song, Q. & Cheng, G. Benefit of interpolation in nearest neighbor algorithms. Preprint at

https://arxiv.org/pdf/1909.11720.pdf (2019). * Cybenko, G. Approximation by superpositions of a sigmoidal function. _Math. Control Signals Syst._ 2, 303–314 (1989). Article  MathSciNet 

Google Scholar  * Jacot, A., Gabriel, F. & Hongler, C. Neural tangent kernel: convergence and generalization in neural networks. In _Advances in Neural Information Processing Systems_

Vol. 31, 8571–8580 (NIPS, 2018). * Goodfellow, I., Bengio, Y. & Courville, A. _Deep Learning_ (MIT Press, 2016). * Bartlett, P. L. For valid generalization the size of the weights is

more important than the size of the network. In _Advances in Neural Information Processing Systems_ Vol. 9, 134–140 (NIPS, 1997). * Neyshabur, B., Tomioka, R. & Srebro, N. In search of

the real inductive bias: on the role of implicit regularization in deep learning. Preprint at https://arxiv.org/pdf/1412.6614.pdf (2014). * Heaven, W. D. Our weird behavior during the

pandemic is messing with AI models. _MIT Technology Review_ (11 May 2020). * Goodfellow, I. J., Shlens, J. & Szegedy, C. Explaining and harnessing adversarial examples. Preprint at

https://arxiv.org/pdf/1412.6572.pdf (2014). * Engstrom, L., Tran, B., Tsipras, D., Schmidt, L. & Madry, A. A rotation and a translation suffice: fooling CNNs with simple transformations.

In _International Conference on Learning Representations_ (ICLR, 2018). * Ma, S., Bassily, R. & Belkin, M. The power of interpolation: understanding the effectiveness of SGD in modern

over-parametrized learning. In _International Conference on Machine Learnin_g 3325–3334 (PMLR, 2018). * Mitra, P. P. Fast convergence for stochastic and distributed gradient descent in the

interpolation limit. In _Proc. 26th European Signal Processing Conference_ (_EUSIPCO_) 1890–1894 (IEEE, 2018). * Loog, M., Viering, T., Mey, A., Krijthe, J. H. & Tax, D. M. A brief

prehistory of double descent. _Proc. Natl Acad. Sci. USA_ 117, 10625–10626 (2020). Article  Google Scholar  * Engel, A. & Van den Broeck, C. _Statistical Mechanics of Learning_

(Cambridge Univ. Press, 2001). * Hastie, T., Montanari, A., Rosset, S. & Tibshirani, R. J. Surprises in high-dimensional ridgeless least squares interpolation. Preprint at

https://arxiv.org/pdf/1903.08560.pdf (2019). * Mitra, P. P. Understanding overfitting peaks in generalization error: analytical risk curves for _l_2 and _l_1 penalized interpolation.

Preprint at https://arxiv.org/pdf/1906.03667.pdf (2019). * Adlam, B. & Pennington, J. The neural tangent kernel in high dimensions: triple descent and a multi-scale theory of

generalization. In _International Conference on Machine Learning_ 74–84 (PMLR, 2020). * Hessel, M. et al. Rainbow: combining improvements in deep reinforcement learning. In _Proc. 32nd AAAI

Conference on Artificial Intelligence_ (AAAI, 2018); https://ojs.aaai.org/index.php/AAAI/article/view/11796 * Fehér, O., Wang, H., Saar, S., Mitra, P. P. & Tchernichovski, O. De novo

establishment of wild-type song culture in the zebra finch. _Nature_ 459, 564–568 (2009). Article  Google Scholar  * Chomsky, N. et al. _Language and Problems of Knowledge_: _The Managua

Lectures_ Vol. 16 (MIT Press, 1988). * Ronneberger, O., Fischer, P. & Brox, T. U-Net: convolutional networks for biomedical image segmentation. In _International Conference on Medical

Image Computing and Computer-Assisted Intervention_ 234–241 (Springer, 2015). * Sutton, R. S. & Barto, A. G. _Reinforcement Learning_: _An Introduction_ (MIT Press, 2018). * Hochreiter,

S. & Schmidhuber, J. Long short-term memory. _Neural Comput._ 9, 1735–1780 (1997). Article  Google Scholar  * Vaswani, A. et al. Attention is all you need. In _Advances in Neural

Information Processing Systems_ Vol. 30, 5998–6008 (NIPS, 2017). * Abraham, T. H. (Physio)logical circuits: the intellectual origins of the McCulloch–Pitts neural networks. _J. History

Behav. Sci._ 38, 3–25 (2002). Article  Google Scholar  * Turing, A. M. _Intelligent Machinery_ (National Physical Laboratory, 1948). * LeCun, Y., Bengio, Y. & Hinton, G. Deep learning.

_Nature_ 521, 436–444 (2015). Article  Google Scholar  * Sillito, A. M., Cudeiro, J. & Jones, H. E. Always returning: feedback and sensory processing in visual cortex and thalamus.

_Trends Neurosci._ 29, 307–316 (2006). Article  Google Scholar  * Bohland, J. W. et al. A proposal for a coordinated effort for the determination of brainwide neuroanatomical connectivity in

model organisms at a mesoscopic scale. _PLoS Comput. Biol._ 5, e1000334 (2009). Article  Google Scholar  * Mitra, P. P. The circuit architecture of whole brains at the mesoscopic scale.

_Neuron_ 83, 1273–1283 (2014). Article  Google Scholar  * Oh, S. W. et al. A mesoscale connectome of the mouse brain. _Nature_ 508, 207–214 (2014). Article  Google Scholar  * Scheffer, L. K.

et al. A connectome and analysis of the adult Drosophila central brain. _eLife_ 9, e57443 (2020). Article  Google Scholar  * Majka, P. et al. Unidirectional monosynaptic connections from

auditory areas to the primary visual cortex in the marmoset monkey. _Brain Struct. Funct._ 224, 111–131 (2019). Article  Google Scholar  * Kaelbling, L. P. The foundation of efficient robot

learning. _Science_ 369, 915–916 (2020). Article  Google Scholar  * Muñoz-Castaneda, R. et al. Cellular anatomy of the mouse primary motor cortex. Preprint at _bioRxiv_

https://doi.org/10.1101/2020.10.02.323154 (2020). * Schmidt, M. & Lipson, H. Distilling free-form natural laws from experimental data. _Science_ 324, 81–85 (2009). Article  Google

Scholar  * Katz, Y. Noam Chomsky on where artificial intelligence went wrong. _The Atlantic_ (1 November 2012). * Acosta, G., Smith, E. & Kreinovich, V. Need for a careful comparison

between hypotheses: case study of epicycles. In _Towards Analytical Techniques for Systems Engineering Applications_ 61–64 (Springer, 2020). * Landauer, R. Irreversibility and heat

generation in the computing process. _IBM J. Res. Dev._ 5, 183–191 (1961). Article  MathSciNet  Google Scholar  * Feynman, R. P. _Feynman Lectures on Computation_ (CRC Press, 2018). Download

references ACKNOWLEDGEMENTS This work was supported by the Crick–Clay Professorship (CSHL) and the H. N. Mahabala Chair Professorship (IIT Madras). AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * Cold Spring Harbor Laboratory Cold Spring Harbor, New York, NY, USA Partha P. Mitra * Center for Computational Brain Research, IIT, Madras, India Partha P. Mitra Authors *

Partha P. Mitra View author publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHOR Correspondence to Partha P. Mitra. ETHICS DECLARATIONS COMPETING

INTERESTS The author declares no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Machine Intelligence_ thanks Samet Oymak and the other, anonymous, reviewer(s)

for their contribution to the peer review of this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mitra, P.P. Fitting elephants in modern machine learning by statistically consistent

interpolation. _Nat Mach Intell_ 3, 378–386 (2021). https://doi.org/10.1038/s42256-021-00345-8 Download citation * Received: 26 November 2019 * Accepted: 15 April 2021 * Published: 19 May

2021 * Issue Date: May 2021 * DOI: https://doi.org/10.1038/s42256-021-00345-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative