Anapole superconductivity from $${{{{{{{\mathcal{pt}}}}}}}}$$ -symmetric mixed-parity interband pairing

ABSTRACT Recently, superconductivity with spontaneous time-reversal or parity symmetry breaking is attracting much attention owing to its exotic properties, such as nontrivial topology and

nonreciprocal transport. Particularly fascinating phenomena are expected when the time-reversal and parity symmetry are simultaneously broken. This work shows that time-reversal

symmetry-breaking mixed-parity superconducting states generally exhibit an unusual asymmetric Bogoliubov spectrum due to nonunitary interband pairing. For generic two-band models, we derive

the necessary conditions for the asymmetric Bogoliubov spectrum. We also demonstrate that the asymmetric Bogoliubov quasiparticles lead to the effective anapole moment of the superconducting

state, which stabilizes a nonuniform Fulde-Ferrell-Larkin-Ovchinnikov state at zero magnetic fields. The concept of anapole order employed in nuclear physics, magnetic materials science,

strongly correlated electron systems, and optoelectronics is extended to superconductors by this work. Our conclusions are relevant for any multiband superconductors with competing even- and

odd-parity pairing channels. Especially, we discuss the superconductivity in UTe2. SIMILAR CONTENT BEING VIEWED BY OTHERS UNCONVENTIONAL GAPPING BEHAVIOUR IN A KAGOME SUPERCONDUCTOR Article

28 February 2025 TOPOLOGICAL SUPERCONDUCTIVITY FROM UNCONVENTIONAL BAND DEGENERACY WITH CONVENTIONAL PAIRING Article Open access 12 September 2024 TOPOLOGICAL TRIPLET-SUPERCONDUCTIVITY IN

SPIN-1 SEMIMETAL Article Open access 07 September 2022 INTRODUCTION Parity symmetry (\({{{{{{{\mathcal{P}}}}}}}}\)-symmetry) and time-reversal symmetry

(\({{{{{{{\mathcal{T}}}}}}}}\)-symmetry) are fundamental properties of quantum materials, such as insulators, metals, magnets, and superconductors. Superconductivity is caused by the quantum

condensation of either even-parity or odd-parity Cooper pairs, which correspond to spin-singlet or spin-triplet superconductivity due to the fermion antisymmetry1. The order parameter of

conventional superconductors breaks neither \({{{{{{{\mathcal{P}}}}}}}}\)-symmetry nor \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry. However, competition and coexistence of multiple pairing

instabilities lead to exotic superconductivity, such as chiral superconductivity with spontaneous \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking2 related to the nontrivial topology3,4 and

anomalous transport5. In particular, mixed-parity superconductivity with coexistent even- and odd-parity pairing channels has been widely discussed in noncentrosymmetric superconductors6,7,

ultracold fermion systems8,9, and spin-orbit-coupled systems in the vicinity of the \({{{{{{{\mathcal{P}}}}}}}}\)-symmetry broken phase10,11,12,13,14. The

\({{{{{{{\mathcal{P}}}}}}}}\)-symmetry is broken in such superconductors. Furthermore, spontaneous \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking realized by the ±_π_/2 phase difference

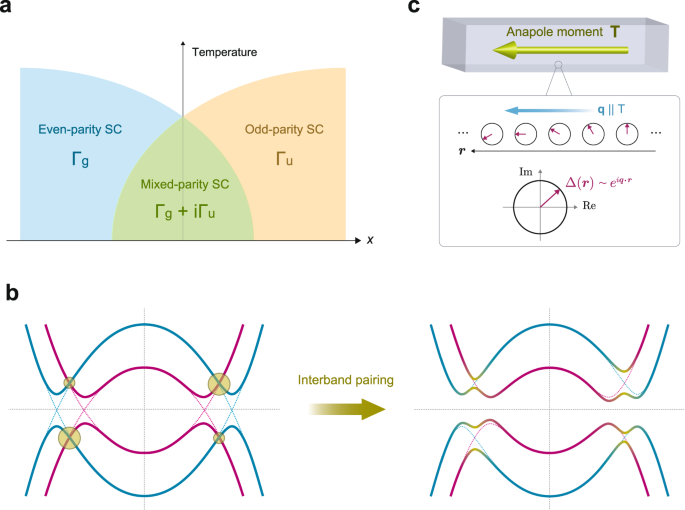
between even- and odd-parity pairing potentials is energetically favored15,16,17 (Fig. 1a), when the spin-orbit coupling (SOC) due to noncentrosymmetric crystal structure is absent or weak.

This class of superconducting states spontaneously breaks both \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries but maintain the combined

\({{{{{{{\mathcal{PT}}}}}}}}\)-symmetry. There have been considerable interests in studying such \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity superconductivity. The

three-dimensional _s_ + _i__p_-wave superconductivity has attracted much theoretical attention as a superconducting analog of axion insulators18,19,20,21,22,23. The

\({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity pairing has also been theoretically proposed in Sr2RuO424. Furthermore, a mixed-parity superconducting state in UTe225 has been

predicted to explain experimentally-observed multiple superconducting phases26,27,28,29,30,31,32,33. In previous works, the mixed-parity superconductivity has been theoretically studied

mainly in single-band models for spin-1/2 fermions15,16,18,19,20,21,23. On the other hand, it has recently been recognized that the multiband structure of the Cooper pair’s wave function

arising from internal electronic degrees of freedom (DOF) (e.g., orbital and sublattice) induces exotic superconducting phenomena. For instance, multiband superconductors have attracted much

attention as a platform realizing odd-frequency pairing34. In \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking superconductors, an intrinsic anomalous Hall effect emerges owing to the

multiband nature of Cooper pairs5,35,36,37,38. In particular, even-parity \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking superconductors host topologically protected Bogoliubov Fermi

surfaces in the presence of interband pairing39,40. In this work, we show that \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity superconducting states generally exhibit an asymmetric

Bogoliubov spectrum (BS) in multiband systems, although it is overlooked in single-band models. We demonstrate that such asymmetric deformation of the BS is induced by a nonunitary interband

pairing (see Fig. 1b), and derive the necessary conditions for generic two-band models. Although we consider two-band systems for simplicity throughout this paper, our theory is relevant

for any multiband superconductors with multiple bands near the Fermi level. In addition, we show that the Bogoliubov quasiparticles with asymmetric BS stabilize the

Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) superconductivity41,42, which is evident from the Lifshitz invariants43, namely linear gradient terms, in the Ginzburg-Landau free energy. The

Lifshitz invariants are nonzero only for the anapole superconducting states, whose order parameters are equivalent to an anapole (magnetic toroidal) moment, namely a polar and time-reversal

odd multipole44, from the viewpoint of symmetry. It is shown that the phase of the superconducting order parameter is spatially modulated along the effective anapole moment of the

superconducting state (see Fig. 1c). The concept of anapole order has been employed in nuclear physics45, magnetic materials science44, strongly correlated electron systems46,47, and

optoelectronics48,49, and it is extended to superconductors by this work. In previous works, the FFLO superconductivity has been proposed in the presence of an external magnetic

field41,42,43,50 or coexistent magnetic multipole order51,52. However, the magnetic field causes superconducting vortices, prohibiting pure FFLO states, and the proposed multipole

superconducting state has not been established in condensed matters. In contrast, the anapole superconductivity realizes the FFLO state without the aid of any other perturbation or

electronic order. Note that an intrinsic nonuniform superconducting state has also been discussed in the Bogoliubov Fermi surface states53, although its mechanism and symmetry are different

from those of the anapole FFLO state. Based on the obtained results, we predict the possible asymmetric BS and anapole superconductivity in UTe2, a recently-discovered candidate of a

spin-triplet superconductor54. The multiple pairing instabilities26,27,28,29,30,31,32,33 and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking55,56,57,58 were recently observed there. RESULTS

GENERAL TWO-BAND BOGOLIUBOV-DE GENNES HAMILTONIAN We begin our discussion by considering the general form of the Bogoliubov-de Gennes (BdG) Hamiltonian for two-band systems:

$${{{{{{{\mathcal{H}}}}}}}}=\frac{1}{2}\mathop{\sum}\limits_{{{{{{{{\bf{k}}}}}}}}}({\hat{c}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}}

},{\hat{c}}_{-{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{T}}}}}}}}})\left(\begin{array}{cc}{H}_{0}({{{{{{{\bf{k}}}}}}}})&{{\Delta }}({{{{{{{\bf{k}}}}}}}})\\ {{{\Delta }}}^{{{{\dagger}}}

}({{{{{{{\bf{k}}}}}}}})&-{H}_{0}^{* }(-{{{{{{{\bf{k}}}}}}}})\end{array}\right)\left(\begin{array}{c}{\hat{c}}_{{{{{{{{\bf{k}}}}}}}}}\\ {\hat{c}}_{-{{{{{{{\bf{k}}}}}}}}}^{*

}\end{array}\right),$$ (1) where \({\hat{c}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{T}}}}}}}}}=({c}_{{{{{{{{\bf{k}}}}}}}}1\uparrow },{c}_{{{{{{{{\bf{k}}}}}}}}1\downarrow

},{c}_{{{{{{{{\bf{k}}}}}}}}2\uparrow },{c}_{{{{{{{{\bf{k}}}}}}}}2\downarrow })\) is a spinor encoding the four internal electronic DOF stem from spin-1/2 and extra two-valued DOF, such as

orbitals and sublattices. Then, the 4 × 4 matrices _H_0(K) and Δ(K) can be generally expressed as a linear combination of _σ__μ_ ⊗ _τ__ν_ matrices, where _σ__μ_ and _τ__ν_ (_μ_, _ν_ = 0, 

_x_, _y_, _z_) are the Pauli matrices for the spin and extra DOF, respectively. However, we here introduce a more convenient form of the two-band BdG Hamiltonian using the Euclidean Dirac

matrices _γ__n_ (_n_ = 1, 2, 3, 4, 5), which satisfy {_γ__m_, _γ__n_} = 2_δ__m__n_. See “Methods” for the correspondence between the _σ__μ_ ⊗ _τ__ν_ and Dirac matrices. Assuming that the

normal state preserves both \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, the general form of the normal state Hamiltonian _H_0(K) can be expressed as

$${H}_{0}({{{{{{{\bf{k}}}}}}}})=({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{0}-\mu ){{{{{{{{\bf{1}}}}}}}}}_{4}+{{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot

{{{{{{{\boldsymbol{\gamma }}}}}}}},$$ (2) where 14 is the 4 × 4 unit matrix, _Γ_ = (_γ_1, _γ_2, _γ_3, _γ_4, _γ_5) is the vector of the five Dirac matrices, \({\epsilon

}_{{{{{{{{\bf{k}}}}}}}}}^{0}\) and \({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}=({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{1},{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{2},{\epsilon

}_{{{{{{{{\bf{k}}}}}}}}}^{3},{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{4},{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{5})\) are the real-valued coefficients of these matrices, and _μ_ is the chemical

potential. Whereas \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{0}\) is an even function of momentum, K-parity of other coefficients \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{n}\) (_n_ > 0) depends

on the details of the extra DOF. The superconducting state is assumed to be a mixture of even- and odd-parity pairing components. The pairing potential Δ(K) for such mixed-parity

superconducting states has the general form $$\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})={{{\Delta }}}_{1}({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{0}{{{{{{{{\bf{1}}}}}}}}}_{4}+{{{{{{{{\boldsymbol{\eta

}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot {{{{{{{\boldsymbol{\gamma }}}}}}}})+{{{\Delta }}}_{2}\mathop{\sum}\limits_{m < n}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn}i{\gamma }_{m}{\gamma }_{n},$$

(3) where \(\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})\equiv {{\Delta }}({{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }\) and _U_T is the unitary part of the time-reversal

operator. The complex-valued constants Δ1 and Δ2 represent the superconducting order parameters for the even- and odd-parity pairing channels, respectively. As a consequence of the fermionic

antisymmetry Δ(K) = − ΔT( − K), the even-parity (odd-parity) part of \(\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})\) is expressed by a linear combination of 14 and _γ__n_ (_i__γ__m__γ__n_) as

shown in Eq. (3) (see “Methods”). The real-valued functions \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{0}\), \({{{{{{{{\boldsymbol{\eta }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}=({\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{1},{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{2},{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{3},{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{4},{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{5})\), and \({\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{mn}\) (1 ≤ _m_ < _n_ ≤ 5) determine the details of order parameters. Whereas \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{0}\) is an even function of momentum, K-parity of

others \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{n}\) and \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn}\) depends on the details of the extra DOF. Note that the K-parity of \({\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{n}\) must be the same as that of \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{n}\). Although we adopt a BCS-type description of superconductivity in this work, we consider

that our argument is hardly affected by enhanced quantum fluctuations in low-dimensional systems when the long-range order occurs. ASYMMETRIC BS FROM

\({{{{{{{\MATHCAL{PT}}}}}}}}\)-SYMMETRIC MIXED-PARITY INTERBAND PAIRING We here consider general BdG Hamiltonian including more than two band models, and later focus on the two-band models.

In the following, we assume that each band is weakly coupled and the intraband pairing is dominant compared to the interband pairing. In such situations, spontaneous

\({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking with maintaining the \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetry is energetically favored in the mixed-parity superconducting states15,16, and the

symmetry of the superconducting order parameter becomes equivalent to that of odd-parity magnetic multipoles44. A characteristic feature of the odd-parity magnetic multipole ordered state

is the asymmetric modulation of the band structure51,52,59,60, which leads to peculiar nonequilibrium responses such as nonreciprocal transport61, magnetopiezoelectric effect62,63, and

photocurrent generation48,49. Therefore, the appearance of the asymmetric BS is naturally expected in the \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity superconductors. However, the

asymmetric BS is not obtained in single-band models (see later discussions). To induce such asymmetric modulation in the BS, effects of the \({{{{{{{\mathcal{P}}}}}}}}\)- and

\({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking in the particle-particle superconducting channel should be transferred into the particle-hole channel. This suggests that it is not sufficient

to consider only the pairing potential Δ(K), since it is not gauge invariant. Instead of Δ(K) alone, we need to consider gauge-invariant bilinear products of Δ(K) and Δ†(K)36 in order to

reveal conditions for realizing the asymmetric BS. Here, we focus on the simplest bilinear products, that is, Δ(K)Δ†(K). The parity-odd and time-reversal-odd

(\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd) part of this bilinear product is calculated as $${M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})=\frac{1}{2}\left([{\hat{{{\Delta

}}}}^{{{{{{{{\rm{g}}}}}}}}}({{{{{{{\bf{k}}}}}}}}),{\hat{{{\Delta }}}}^{{{{{{{{\rm{u{{{\dagger}}}}}}} }}}}}({{{{{{{\bf{k}}}}}}}})]+[{\hat{{{\Delta

}}}}^{{{{{{{{\rm{u}}}}}}}}}({{{{{{{\bf{k}}}}}}}}),{\hat{{{\Delta }}}}^{{{{{{{{\rm{g{{{\dagger}}}}}}} }}}}}({{{{{{{\bf{k}}}}}}}})]\right),$$ (4) where \({\hat{{{\Delta

}}}}^{{{{{{{{\rm{g}}}}}}}}}({{{{{{{\bf{k}}}}}}}})\) and \({\hat{{{\Delta }}}}^{{{{{{{{\rm{u}}}}}}}}}({{{{{{{\bf{k}}}}}}}})\) are the even- and odd-parity part of \(\hat{{{\Delta

}}}({{{{{{{\bf{k}}}}}}}})\), respectively (see Supplementary Note 1 for the derivation of Eq. (4)). Owing to the gauge invariance and

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd behavior of \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\), a nonzero \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) can be a measure of the

\({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking in the particle-hole channel, which permits emergence of the asymmetric BS. Note that the pairing state

must be nonunitary to induce a nonzero \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\), since \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})=0\) when Δ(K)Δ†(K) is proportional to the unit matrix. In analogy

with the spin polarization of nonunitary spin-triplet superconducting states in spin-1/2 single-band models1, the \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd bilinear product

\({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) can be interpreted as a polarization of an internal DOF in the superconducting state. The emergence of a nonzero

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd bilinear product \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) requires the interband pairing. To see this, we consider the problem in

the band basis. Since _H_0(K) is assumed to preserve the \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, the energy eigenvalues are doubly degenerate and labeled

by a pseudospin index. Especially, we choose the so-called manifestly covariant Bloch basis10, in which the pseudospin index transforms like a true spin-1/2 under time-reversal and

crystalline symmetry operations. In this basis, the intraband pairing potential is generally expressed as ΔK = (_ψ_K + DK ⋅ S)_i__s__y_, where S = (_s__x_, _s__y_, _s__z_) are Pauli matrices

in pseudospin space. The complex-valued functions _ψ_K and DK are even and odd functions of K, respectively. Then, in the absence of the interband pairing, the multiband BdG Hamiltonian

matrix reduces to a series of decoupled blocks describing spin-1/2 single-band superconductors. The bilinear product for this intraband pairing potential is obtained as \({{{\Delta

}}}_{{{{{{{{\bf{k}}}}}}}}}{{{\Delta }}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }=(| {\psi }_{{{{{{{{\bf{k}}}}}}}}}{| }^{2}+| {{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}{|

}^{2}){{{{{{{{\bf{1}}}}}}}}}_{2}+2{{{{{{{\rm{Re}}}}}}}}({\psi }_{{{{{{{{\bf{k}}}}}}}}}{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{* })\cdot

{{{{{{{\bf{s}}}}}}}}+i({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\times {{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{* })\cdot {{{{{{{\bf{s}}}}}}}}\), and the second and third terms are

nonunitary components that break \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, respectively. Here, 12 is the 2 × 2 unit matrix. However, there appears no term

breaking both \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, and hence the \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd bilinear product for

this ΔK must vanish. This indicates that the interband pairing is necessary for a nonzero \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd bilinear product

\({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\), which is essential for realizing the asymmetric BS. This is also the reason the asymmetric BS is not obtained in single-band models. The presence of

interband pairing can be characterized by the so-called superconducting fitness _F_(K), which is defined as

\(F({{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}}={H}_{0}({{{{{{{\bf{k}}}}}}}}){{\Delta }}({{{{{{{\bf{k}}}}}}}})-{{\Delta }}({{{{{{{\bf{k}}}}}}}}){H}_{0}^{*

}(-{{{{{{{\bf{k}}}}}}}})\)64,65. Since a nonvanishing _F_(K)_F_†(K) quantifies the strength of interband pairing by definition64,65, its

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd part should be nonzero to realize a nonvanishing \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\). The

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd part of _F_(K)_F_†(K) is obtained as

$${M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}})=\frac{1}{2}\left([{F}^{{{{{{{{\rm{g}}}}}}}}}({{{{{{{\bf{k}}}}}}}}),{F}^{{{{{{{{\rm{u{{{\dagger}}}}}}}

}}}}}({{{{{{{\bf{k}}}}}}}})]+[{F}^{{{{{{{{\rm{u}}}}}}}}}({{{{{{{\bf{k}}}}}}}}),{F}^{{{{{{{{\rm{g{{{\dagger}}}}}}} }}}}}({{{{{{{\bf{k}}}}}}}})]\right),$$ (5) where _F_g(K) and _F_u(K) are the

even- and odd-parity part of _F_(K), respectively. If the normal state preserves both \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, they are obtained as

\({F}^{{{{{{{{\rm{g,u}}}}}}}}}({{{{{{{\bf{k}}}}}}}})=[{H}_{0}({{{{{{{\bf{k}}}}}}}}),{\hat{{{\Delta }}}}^{{{{{{{{\rm{g,u}}}}}}}}}({{{{{{{\bf{k}}}}}}}})]\). Note that the

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd part of _F_(K)_F_†(K) can be extracted in the same way as Δ(K)Δ†(K) [compare Eq. (5) with Eq. (4)], since the transformation of

_F_(K)_F_†(K) under space-inversion and time-reversal can be described in the same way as that of Δ(K)Δ†(K). Based on Eq. (5), not only the pair potential Δ(K) but also the normal part

_H_0(K) must satisfy a proper condition to realize \({M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\) and asymmetric BS. From the above discussions, we conclude that the necessary (but not

sufficient) condition for the asymmetric BS can be written as \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\,\cap \,{M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\), which implies the

superconductivity-driven \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking in the particle-hole channel. We here write down this necessary condition for the

general two-band BdG Hamiltonian. By substituting Eqs. (2) and (3) to Eqs. (4) and (5), we obtain the \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd bilinear products

\({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) and \({M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}})\) as follows: $${M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})=2{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta

}}}_{2}^{* })\mathop{\sum}\limits_{m < n}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn}({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{n}{\gamma }_{m}-{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{m}{\gamma }_{n}),$$ (6)

$${M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}})={{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]{\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}}),$$ (7) where

\({\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})\equiv {H}_{0}({{{{{{{\bf{k}}}}}}}})-({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{0}-\mu ){{{{{{{{\bf{1}}}}}}}}}_{4}\). We see that

\({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) appears inside the expression of \({M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}})\), and hence the necessary condition for the asymmetric BS can be simplified as

\({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})] \, \ne \, 0\) in two-band models. Note that it is not clear whether

\({M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}})\) can be written in terms of \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})\) in more than two band models since Eq. (7) is derived for the general two-band

model by using the properties of Dirac matrices. From Eqs. (6) and (7), the necessary condition (i.e.,

\({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})] \, \ne \, 0\)) can be summarized as following two criteria; (i) the relative phase

difference between even- and odd-parity pairing potentials must be nonzero so that \({{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* })\ne 0\), and (ii) the BdG Hamiltonian must

satisfy \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{m}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{n}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn} \, \ne \, 0\) or \({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{n}{\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{m}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn} \, \ne \, 0\) for 1 ≤ ∃_m_ < ∃_n_ ≤ 5. Interpretations of these requirements in the _σ__μ_ ⊗ _τ__ν_ basis are shown in

“Methods” section. We now confirm that the asymmetric BS indeed appears when the above two criteria are fulfilled. A minimal two-band model satisfying the criterion (ii) can be obtained by

substituting \({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}=r{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a}{{{{{{{{\bf{e}}}}}}}}}_{a}+(1-r){\epsilon

}_{{{{{{{{\bf{k}}}}}}}}}^{b}{{{{{{{{\bf{e}}}}}}}}}_{b}\), \({{{{{{{{\boldsymbol{\eta }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}=(1-r){\eta }_{{{{{{{{\bf{k}}}}}}}}}^{a}{{{{{{{{\bf{e}}}}}}}}}_{a}+r{\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{b}{{{{{{{{\bf{e}}}}}}}}}_{b}\), and \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{mn}={\delta }_{ma}{\delta }_{nb}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}\) into Eqs. (2) and (3).

Here, _a_ and _b_ are specific integers satisfying 1 ≤ _a_ < _b_ ≤ 5, E_n_ is the unit vector for the _n_-th component, and _r_ takes the value either 0 or 1. Under this setup, we can

analytically diagonalize the BdG Hamiltonian as

\({{{{{{{\rm{diag}}}}}}}}({E}_{{{{{{{{\bf{k}}}}}}}}}^{+}{{{{{{{{\bf{1}}}}}}}}}_{2},{E}_{{{{{{{{\bf{k}}}}}}}}}^{-}{{{{{{{{\bf{1}}}}}}}}}_{2},-{E}_{-{{{{{{{\bf{k}}}}}}}}}^{+}{{{{{{{{\bf{1}}}}}}}}}_{2},-{E}_{-{{{{{{{\bf{k}}}}}}}}}^{-}{{{{{{{{\bf{1}}}}}}}}}_{2})\).

Based on the correspondence between the Dirac matrices and _σ__μ_ ⊗ _τ__ν_ matrices the energy spectrum \({E}_{{{{{{{{\bf{k}}}}}}}}}^{\pm }\) can be obtained as

$${E}_{{{{{{{{\bf{k}}}}}}}}}^{\pm }= \sqrt{{\xi }_{{{{{{{{\bf{k}}}}}}}}}^{2}+\frac{1}{4}{{{{{{{\rm{Tr}}}}}}}}\left[{{\Delta }}({{{{{{{\bf{k}}}}}}}}){{{\Delta }}}^{{{{\dagger}}}

}({{{{{{{\bf{k}}}}}}}})\pm \frac{{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})}{r{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a}+(1-r){\epsilon

}_{{{{{{{{\bf{k}}}}}}}}}^{b}}\right]}\\ \pm \, [r{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a}+(1-r){\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{b}],$$ (8) where \({\xi }_{{{{{{{{\bf{k}}}}}}}}}\equiv

{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{0}-\mu\). By using the transformation properties of the BdG Hamiltonian under space-inversion and time-reversal, we can confirm that Eq. (8) satisfies

\({E}_{-{{{{{{{\bf{k}}}}}}}}}^{+}\ne {E}_{{{{{{{{\bf{k}}}}}}}}}^{\pm }\) and \({E}_{-{{{{{{{\bf{k}}}}}}}}}^{-}\ne {E}_{{{{{{{{\bf{k}}}}}}}}}^{\pm }\) (i.e., the BS is asymmetric) when

\({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})] \, \ne \, 0\). See “Methods” for the proof. This implies that

\({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\,\cap \,{M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\) is indeed a necessary condition of the asymmetric BS. LIFSHITZ INVARIANTS AND

EFFECTIVE ANAPOLE MOMENT To obtain further insight into the asymmetric BS, we now investigate the free energy of the above minimal model satisfying \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}) \,

\ne \, 0\,\cap \,{M}_{-}^{(2)}({{{{{{{\bf{k}}}}}}}}) \, \ne \, 0\). By differentiating Eq. (8) with respect to Δ_j_ and \({{{\Delta }}}_{j}^{* }\) (_j_ = 1, 2), the Ginzburg-Landau free

energy for superconductivity is derived as follows (see Supplementary Note 2): $${{{{{{{\mathcal{F}}}}}}}}= \,\, {\alpha }_{1}| {{{\Delta }}}_{1}{| }^{2}+{\alpha }_{2}| {{{\Delta }}}_{2}{|

}^{2}+{\beta }_{1}| {{{\Delta }}}_{1}{| }^{4}+{\beta }_{2}| {{{\Delta }}}_{2}{| }^{4}\\ +\,4\tilde{\beta }| {{{\Delta }}}_{1}{| }^{2}| {{{\Delta }}}_{2}{| }^{2}-\tilde{\beta }({{{\Delta

}}}_{1}^{2}{{{\Delta }}}_{2}^{* 2}+{{{\Delta }}}_{2}^{2}{{{\Delta }}}_{1}^{* 2})\\ +\,\mathop{\sum}\limits_{\nu =x,y,z}({\kappa }_{1,\nu }| {{{\Delta }}}_{1}{| }^{2}+{\kappa }_{2,\nu }|

{{{\Delta }}}_{2}{| }^{2}){q}_{\nu }^{2}+{{{{{{{\bf{T}}}}}}}}\cdot {{{{{{{\bf{q}}}}}}}},$$ (9) where Q = (_q__x_, _q__y_, _q__z_) is the center-of-mass momentum of Cooper pairs. The

analytical expressions of _α__j_, _β__j_( > 0), \(\tilde{\beta }( > \, 0)\), and _κ__j_,_ν_( > 0) are shown in Supplementary Note 2. The last term is the Lifshitz invariant43

stabilizing the FFLO state with Q∥T. Since the Cooper pair condensation occurs at a single Q in our model, the superconducting order parameter is expressed as Δ(R) ∝ _e__i_Q⋅R in real space

(Fig. 1c). The coefficient vector T = (_T__x_, _T__y_, _T__z_) is given by $${{{{{{{\bf{T}}}}}}}}={\rho }_{0}{\langle

{{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]{{{{{{{{\bf{v}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\rangle }_{{{{{{{{\rm{FS}}}}}}}}}\frac{7\zeta

(3)}{16{\pi }^{2}{T}^{2}},$$ (10) where _ρ_0 is the density of states at the Fermi energy, 〈⋯ 〉FS denotes the average over the Fermi surface, VK ≡ ∇K_ξ_K, _T_ is the temperature, and

_ζ_(_x_) is the Riemann zeta function. T can be interpreted as the effective anapole moment of the superconducting state. To see this, we here consider conditions for T ≠ 0. Eq. (10)

indicates that T is nonzero only for \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking pairing states with \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}) \, \ne \,

0\). In addition, \({\langle {{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]{{{{{{{{\bf{v}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\rangle

}_{{{{{{{{\rm{FS}}}}}}}}}\) is nonzero only when the superconducting order parameter belongs to a polar irreducible representation (IR), since the velocity VK is a polar vector and

\({\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})\) is assumed to be \({{{{{{{\mathcal{P}}}}}}}}\)-symmetric. Therefore, T is a polar and time-reversal-odd vector; the symmetry is equivalent to the

anapole moment44,45. Hereafter, we refer to the superconductivity with T ≠ 0 as the anapole superconductivity. The anapole superconductivity realizes a nonuniform FFLO state with Q∥T (see

Fig. 1c) to compensate a polar asymmetry in the BS. The \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity pairing is an origin of the anapole superconductivity. Although the stability of

such pairing has been revealed15, a self-consistent calculation is desirable to justify the stability of the anapole FFLO state and clarify the properties further. Such detailed analysis is

left for future work. Finally, we comment that the anapole moment must be aligned in the conducting direction in low-dimensional systems. This restriction naturally appears through the

above expression (10) of the effective anapole moment T. APPLICATION TO UTE2 We now discuss the asymmetric BS and anapole superconductivity in UTe2. Intensive studies after the discovery of

superconductivity evidenced odd-parity spin-triplet superconductivity in UTe254,55,56,66,67,68,69,70,71,72,73,74,75,76,77,78,79. However, multiple superconducting phases similar to Fig. 1a

have been observed under pressure26,27,28,29,30,31,32,33, and the antiferromagnetic quantum criticality implies the spin-singlet superconductivity there31. A theoretical study based on the

periodic Anderson model verified this naive expectation and predicted the parity-mixed superconducting state in the intermediate pressure region25. Note that the interband pairing, which is

an essential ingredient for the asymmetric BS and anapole superconductivity, may have considerable impacts on the superconductivity in UTe2 owing to multiple bands near the Fermi

level25,80,81,82,83,84,85,86. First, let us discuss the symmetry of superconductivity. Since the crystal structure of UTe2 preserves _D_2h point group symmetry, the superconducting order

parameter is classified based on the IRs of _D_2h. Below we consider all the odd-parity IRs, namely, _A_u, _B_1u, _B_2u, and _B_3u, although the _A_u and _B_3u IRs may be promising

candidates25,77,78,80,87. Moreover, a recent calculation has shown that the even-parity _A_g superconducting state is favored by antiferromagnetic fluctuation under pressure25. Therefore, we

study a mixture of the even-parity _A_g and odd-parity either _A_u, _B_1u, _B_2u, or _B_3u states, while we particularly focus on the _A_u or _B_3u pairing. Based on the above facts, we

introduce a minimal model for UTe2 as follows: $${H}_{0}({{{{{{{\bf{k}}}}}}}})=({\varepsilon }_{{{{{{{{\bf{k}}}}}}}}}-\mu ){\sigma }_{0}\otimes {\tau

}_{0}+{{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}\otimes {\tau }_{z},$$ (11) $$\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})=\, {{{\Delta }}}_{1}({\psi

}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}{\sigma }_{0}\otimes {\tau }_{0}+{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma

}}}}}}}}\otimes {\tau }_{z})\\ +\,{{{\Delta }}}_{2}({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}\otimes {\tau }_{0}+{\psi

}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}{\sigma }_{0}\otimes {\tau }_{z}),$$ (12) where _τ__ν_ represent the Pauli matrices for a sublattice DOF originating from a ladder structure of

U atoms (Fig. 2). We assume a simple form of the single-particle kinetic energy as \({\varepsilon }_{{{{{{{{\bf{k}}}}}}}}}=-2{\sum }_{\nu = x,y,z}{t}_{\nu }\cos {k}_{\nu }\). The second

term of Eq. (11) is a sublattice-dependent staggered form of Rashba SOC with \({{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}=\alpha (\sin {k}_{y}\hat{{{{{{{{\bf{x}}}}}}}}}-\sin

{k}_{x}\hat{{{{{{{{\bf{y}}}}}}}}})\), arising from the local \({{{{{{{\mathcal{P}}}}}}}}\)-symmetry breaking at U sites25,88. Since the local site symmetry descends to _C_2v from _D_2h owing

to the ladder structure of U atoms, the existence of the Rashba-type SOC with opposite coupling constants ± _α_ at each sublattice is naturally expected (see Fig. 2). The local

\({{{{{{{\mathcal{P}}}}}}}}\)-symmetry breaking also leads to a sublattice-dependent parity mixing of the pair potential89. Then, the even-parity (odd-parity) pair potential is assumed to be

a mixture of intrasublattice spin-singlet (spin-triplet) and staggered spin-triplet (spin-singlet) components as shown in Eq. (12). We assume the form of the K-dependent coefficients

\({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\) and \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\)

(\({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}\) and \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}\)) so as to be consistent with the basis functions of

the _A_g IR (_A_u, _B_1u, _B_2u, or _B_3u IRs). We now consider the necessary conditions for an asymmetric BS in UTe2. As discussed in the above sections, a nonzero

\({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]\) is necessary for the asymmetric BS in a two-band model. For Eqs. (11) and (12), this

quantity is obtained as \({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]=-8{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{*

})[{{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot ({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\times

{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}})]\). Therefore, \({{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot

({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\times {{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}) \, \ne \, 0\) must be satisfied to realize

the asymmetric BS. This indicates that the sublattice-dependent SOC and spin-triplet pairing components \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g,u}}}}}}}}}\) are

essential for the asymmetric BS. In contrast, the spin-singlet pairing components \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g,u}}}}}}}}}\) do not play an important role for realizing the

asymmetric BS in this model. Hereafter, we assume \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}=1\) and \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}=0\) for simplicity.

The basis functions of \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g,u}}}}}}}}}\) and corresponding \({{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot

({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\times {{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}})\) for possible mixed-parity superconducting

states in UTe2 are summarized in Table 1. As shown in Table 1, \({{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot

({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\times {{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}})\propto \alpha ({\phi

}_{x}^{{{{{{{{\rm{g}}}}}}}}}+{\phi }_{y}^{{{{{{{{\rm{g}}}}}}}}}){\phi }_{z}^{{{{{{{{\rm{u}}}}}}}}}\) for all patterns of the superconducting state, where \({\phi }_{\nu

}^{{{{{{{{\rm{g,u}}}}}}}}}\) is a real-valued coefficient of the _ν_-th component of \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g,u}}}}}}}}}\). Therefore, \({\phi

}_{x}^{{{{{{{{\rm{g}}}}}}}}}+{\phi }_{y}^{{{{{{{{\rm{g}}}}}}}}} \, \ne \, 0\) and \({\phi }_{z}^{{{{{{{{\rm{u}}}}}}}}} \, \ne \, 0\) are necessary for the asymmetric BS. According to a

recent numerical calculation25, the magnetic anisotropy of UTe2 leads to \(| {\phi }_{y}^{{{{{{{{\rm{g}}}}}}}}}| \gg | {\phi }_{x}^{{{{{{{{\rm{g}}}}}}}}}|\) for the _A_g state. Then, we

assume \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}=\sin {k}_{x}\hat{{{{{{{{\bf{y}}}}}}}}}\) (i.e., \({\phi }_{x}^{{{{{{{{\rm{g}}}}}}}}}=0\) and \({\phi

}_{y}^{{{{{{{{\rm{g}}}}}}}}}=1\)) in the following calculations. On the other hand, we assume \({\phi }_{\nu }^{{{{{{{{\rm{u}}}}}}}}}={\delta }_{\nu z}\) for the odd-parity pairing component

to extract only the essential ingredient for the asymmetric BS and make a clear discussion. The numerical results of the BS for this UTe2 model are shown in Fig. 3. We here consider only

the _A_g + _i__A_u (\({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}=\sin {k}_{z}\hat{{{{{{{{\bf{z}}}}}}}}}\)) and _A_g + _i__B_3u

(\({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}}=\sin {k}_{y}\hat{{{{{{{{\bf{z}}}}}}}}}\)) states as promising candidates of the

\({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity superconductivity in UTe2. It is shown that the BS of both _A_g + _i__A_u and _A_g + _i__B_3u states are indeed asymmetric along some

directions in the Brillouin zone (see Fig. 3a, b). The BS in the _A_g + _i__A_u state exhibits a _k__x__k__y__k__z_-type tetrahedral asymmetry as depicted in Fig. 3c, while the BS in the

_A_g + _i__B_3u state shows a \({k}_{x}{k}_{y}^{2}\)-type unidirectional asymmetry as depicted in Fig. 3d. Consistent with these numerical results, Table 1 reveals that

\({{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot ({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{g}}}}}}}}}\times

{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{{{{{\rm{u}}}}}}}}})\) of the _A_g + _i__A_u and _A_g + _i__B_3u states are proportional to _k__x__k__y__k__z_ and \({k}_{x}{k}_{y}^{2}\),

respectively. This implies that the type of asymmetry in the BS is determined by the symmetry of

\({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]\), which is an essential ingredient for realizing the asymmetric BS. Finally, we discuss the

possible anapole superconductivity in UTe2. The _A_g + _i__A_u state belongs to the nonpolar \({A}_{{{{{{{{\rm{u}}}}}}}}}^{-}\) IR (IRs with odd time-reversal parity are denoted by Γ−),

which corresponds to nonpolar odd-parity magnetic multipoles such as magnetic monopole, quadrupole, and hexadecapole from the viewpoint of symmetry. On the other hand, the _A_g + _i__B_3u

state belongs to the polar \({B}_{{{{{{{{\rm{3u}}}}}}}}}^{-}\) IR with the polar _x_ axis, which is symmetrically equivalent to the anapole moment _T__x_. Since the anapole superconducting

states are allowed only when the superconducting order parameter belongs to a polar IR, the _A_g + _i__B_3u state is a possible candidate of the anapole superconductivity. Indeed, as

discussed above, the BS of the _A_g + _i__B_3u state exhibits a polar \({k}_{x}{k}_{y}^{2}\)-type asymmetry, while the BS of the _A_g + _i__A_u state exhibits a nonpolar

_k__x__k__y__k__z_-type asymmetry (see Fig. 3). It should also be noted that the BS in the _A_g + _i__B_3u state possesses the polarity along the _k__x_ axis, which coincides with the polar

axis of the \({B}_{{{{{{{{\rm{3u}}}}}}}}}^{-}\) IR. Based on the above classification and the Ginzburg-Landau free energy (9), the anapole FFLO state with \({{{{{{{\bf{q}}}}}}}}\propto

{{{{{{{\bf{T}}}}}}}}\parallel \hat{{{{{{{{\bf{x}}}}}}}}}\) should be naturally realized in the _A_g + _i__B_3u state. In the same manner, we expect the anapole superconducting states with

\({{{{{{{\bf{T}}}}}}}}\parallel \hat{{{{{{{{\bf{y}}}}}}}}}\) and \({{{{{{{\bf{T}}}}}}}}\parallel \hat{{{{{{{{\bf{z}}}}}}}}}\) in the _A_g + _i__B_2u and _A_g + _i__B_1u states, respectively

(see Supplementary Note 3 for possible anapole superconductivity in UTe2). DISCUSSION From the analogy with magnetic states, we can predict various exotic superconducting phenomena closely

related to the asymmetric BS. For instance, the asymmetry of the BS will significantly affect the superconducting piezoelectric effect90, nonreciprocal optical responses91, and nonreciprocal

Meissner effect92. All of these phenomena are caused by the absence of \({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries in the superconducting state. Hence, they

will be useful probes to offer conclusive evidence for the \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-symmetry breaking and the BS asymmetry in superconductors. Studies for the

interplay of these exotic superconducting phenomena and asymmetric BS will be presented elsewhere. Experimental detection of the anapole superconductivity should be possible by observing its

domain structure. The anapole superconducting state effectively carries a supercurrent along the anapole moment T, since the order parameter is spatially modulated with _e__i_Q⋅R ~ 

_e__i_T⋅R. This indicates the emergence of superconducting vortices at the anapole domain boundaries (see Fig. 4a) even though an external magnetic field is absent. The anapole domains can

be generally formed owing to the degeneracy between the Γg + _i_Γu pairing and Γg − _i_Γu pairing states, which have the opposite anapole moment. Therefore, the observation of vortices at a

zero magnetic field can be solid evidence of the anapole superconductivity. In addition, the anapole domain can be switched by the supercurrent in a similar way to the electrical switching

of antiferromagnets93,94. In an anapole superconductor, the effective anapole moment T couples to the applied electric current J, which is a symmetry-adapted field of the anapole moment.

Then, the anapole superconducting domain should be switched to align the effective anapole moments along the injected supercurrent J (see Fig. 4b). It should also be noticed that the anapole

domain switching eliminates the internal magnetic field from the vortices at the domain boundaries, since the domain structure disappears by applying the supercurrent. Therefore, the

anapole superconducting domain switching can be regarded as a process of erasing magnetic information. These properties indicate potential applications of anapole superconductivity as a

novel quantum device for magnetic information storage and processing. CONCLUSIONS In summary, we have established that the \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity

superconductors generally exhibit asymmetry in the BS. The essential ingredient for the asymmetric BS is the \({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd nonunitary part of

the bilinear product ΔΔ† arising from the interband pairing. Therefore, the multiband nature of superconductivity is essential. Especially, we have shown that an FFLO state is stabilized in

the absence of an external magnetic field when the superconducting state belongs to a polar and time-reversal-odd IR. The stabilization of the FFLO state is evidenced by the emergence of

Lifshitz invariants in the free energy due to the effective anapole moment. The physics of asymmetric BS appears in any multiband superconductors when even- and odd-parity pairing

interactions are comparable in strength. As a specific example, we considered the mixed-parity pairing states in UTe2, which is caused by an accidental competition of ferromagnetic and

antiferromagnetic spin fluctuations under pressure25. We have shown that the mixed-parity superconductivity in UTe2 realizes the asymmetric BS and anapole superconductivity owing to the

locally noncentrosymmetric crystal structure. The asymmetric BS may be linked to the asymmetric spectrum in the scanning tunneling microscope measurement55, although it was interpreted based

on the chiral superconductivity. The vortex structure near the anapole domain boundary (Fig. 4a) may also cause the polar Kerr effect, reported for UTe258. Spontaneous ordering of strongly

parity-mixed pairing state and resulting asymmetric BS can also be expected in superconductivity mediated by parity-breaking fluctuations11. To further broaden the scope of application of

our theory, it is important to find microscopic electronic interactions that induce competing even- and odd-parity pairing instabilities. We predicted various superconducting phenomena

induced by the asymmetric BS, such as the superconducting piezoelectric effect, nonlinear optical responses, nonreciprocal Meissner effect, and anapole domain switching from the analogy with

magnetic materials. Topological properties and collective modes associated with the asymmetric BS may also be intriguing issues. Exploration of such exotic phenomena will be a promising

route for future research. METHODS CORRESPONDENCE BETWEEN PAULI MATRICES AND DIRAC MATRICES In this section, we show that the general form of the BdG Hamiltonian with spin-1/2 and a

two-valued extra DOF can be expressed by using the Euclidean Dirac matrices. Since we assume that the normal state preserves both \({{{{{{{\mathcal{P}}}}}}}}\)- and

\({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, _H_0(K) transforms under the space-inversion \({{{{{{{\mathcal{P}}}}}}}}\) and the time-reversal \({{{{{{{\mathcal{T}}}}}}}}\) as

$${H}_{0}({{{{{{{\bf{k}}}}}}}})\mathop{\to }\limits^{{{{{{{{\mathcal{P}}}}}}}}}{U}_{{{{{{{{\rm{P}}}}}}}}}^{{{{\dagger}}}

}{H}_{0}(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{P}}}}}}}}}={H}_{0}({{{{{{{\bf{k}}}}}}}}),$$ (13) $${H}_{0}({{{{{{{\bf{k}}}}}}}})\mathop{\to

}\limits^{{{{{{{{\mathcal{T}}}}}}}}}{U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }{H}_{0}^{* }(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}}={H}_{0}({{{{{{{\bf{k}}}}}}}}),$$ (14) where _U_P

and _U_T are unitary matrices. In this paper, we consider a spin-1/2 system satisfying \({U}_{{{{{{{{\rm{T}}}}}}}}}{U}_{{{{{{{{\rm{T}}}}}}}}}^{* }=-{{{{{{{{\bf{1}}}}}}}}}_{4}\). In addition,

we require that the time-reversal commute with the space-inversion (i.e., \({U}_{{{{{{{{\rm{P}}}}}}}}}{U}_{{{{{{{{\rm{T}}}}}}}}}={U}_{{{{{{{{\rm{T}}}}}}}}}{U}_{{{{{{{{\rm{P}}}}}}}}}^{*

}\)), and the space-inversion operator is its own inverse (i.e., \({U}_{{{{{{{{\rm{P}}}}}}}}}^{2}={{{{{{{{\bf{1}}}}}}}}}_{4}\)). Under the above assumptions, _H_0(K) can be generally

expressed as $${H}_{0}({{{{{{{\bf{k}}}}}}}})=({\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{0}-\mu ){\sigma }_{0}\otimes {\tau }_{0}+{f}_{{{{{{{{\bf{k}}}}}}}}}{\sigma }_{0}\otimes {\tau }_{{x}_{i}}\\

+\,{{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}\otimes {\tau }_{{y}_{i}}+{h}_{{{{{{{{\bf{k}}}}}}}}}{\sigma }_{0}\otimes {\tau }_{{z}_{i}},$$ (15)

where _Σ_ = (_σ__x_, _σ__y_, _σ__z_) and _σ_0 ⊗ _τ_0 = 14. Hermiticity requires all coefficients in Eq (15) are real. The index _i_ specifies the extra DOF and (_x__i_, _y__i_, _z__i_) is a

permutation of (_x_, _y_, _z_). Since _U_P and _U_T vary depending on the extra DOF, the general models (15) are classified by the index _i_. In this paper, we consider three representative

examples shown in Table 2. For _i_ = 1 (_i_ = 2), the extra DOF is orbitals with the same (opposite) parity, and _U_P = _σ_0 ⊗ _τ_0 (_U_P = _σ_0 ⊗ _τ__z_). For _i_ = 3, the extra DOF is

sublattices in a locally noncentrosymmetric crystal structure, and _U_P = _σ_0 ⊗ _τ__x_. In these cases, _U_T = _i__σ__y_ ⊗ _τ_0. Although the extra DOF can be other than the above three

cases, Eq. (15) holds for all the cases unless \({U}_{{{{{{{{\rm{P}}}}}}}}}{U}_{{{{{{{{\rm{T}}}}}}}}}\ne {U}_{{{{{{{{\rm{T}}}}}}}}}{U}_{{{{{{{{\rm{P}}}}}}}}}^{* }\), _U_P_U_P ≠ 14, or

\({U}_{{{{{{{{\rm{T}}}}}}}}}{U}_{{{{{{{{\rm{T}}}}}}}}}^{* }\ne -{{{{{{{{\bf{1}}}}}}}}}_{4}\)37. Since the set of _σ__μ_ ⊗ _τ__ν_ matrices is completely anticommuting in Eq. (15), we can

substitute them by the five anticommuting Euclidean Dirac matrices. Then, we can rewrite Eq. (15) as Eq. (2). The pairing potential Δ(K) transforms under the space-inversion and the

time-reversal as Δ(K) \({{{{{{\mathcal{P}}}}}}}\atop{\longrightarrow}\) \({U}_{{{{{{{{\rm{P}}}}}}}}}^{{{{\dagger}}} }{{\Delta }}(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{P}}}}}}}}}^{* }\) and

Δ(K) \({{{{{{\mathcal{T}}}}}}}\atop{\longrightarrow }\) \({U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }{{{\Delta }}}^{* }(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}}^{* }\), respectively.

In terms of \(\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})={{\Delta }}({{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }\), these relations can be rewritten as $$\hat{{{\Delta

}}}({{{{{{{\bf{k}}}}}}}})\mathop{\to }\limits^{{{{{{{{\mathcal{P}}}}}}}}}{U}_{{{{{{{{\rm{P}}}}}}}}}^{{{{\dagger}}} }\hat{{{\Delta }}}(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{P}}}}}}}}},$$ (16)

$$\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})\mathop{\to }\limits^{{{{{{{{\mathcal{T}}}}}}}}}{\hat{{{\Delta }}}}^{{{{\dagger}}} }({{{{{{{\bf{k}}}}}}}}).$$ (17) We note that Eq. (16) is

equivalent to the transformation of _H_0(K) under the space-inversion [see Eq. (13)], while Eq. (17) corresponds to the Hermiticity condition. Whereas _H_0(K) is assumed to preserve both

\({{{{{{{\mathcal{P}}}}}}}}\)- and \({{{{{{{\mathcal{T}}}}}}}}\)-symmetries, we admit that Δ(K) spontaneously breaks the \({{{{{{{\mathcal{P}}}}}}}}\)- and

\({{{{{{{\mathcal{T}}}}}}}}\)-symmetries. The only requirements for the pairing potential is satisfying the fermionic antisymmetry Δ(K) = − ΔT( − K), which can be rewritten as

$$\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})={U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }{\hat{{{\Delta }}}}^{{{{{{{{\rm{T}}}}}}}}}(-{{{{{{{\bf{k}}}}}}}}){U}_{{{{{{{{\rm{T}}}}}}}}},$$ (18) where

we used the fact that \({U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }={U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{{{{{\rm{T}}}}}}}}}=-{U}_{{{{{{{{\rm{T}}}}}}}}}\) by choosing _U_T as real (i.e.,

\({U}_{{{{{{{{\rm{T}}}}}}}}}={U}_{{{{{{{{\rm{T}}}}}}}}}^{* }\)). It should be noticed that Eq. (18) is formally equivalent to the time-reversal symmetry for _H_0(K) [see Eq. (14)]. Since the

even-parity part of \(\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})\) obeys transformation properties completely equivalent to those of _H_0(K) under the time-reversal and the space-inversion, it

can be expressed as a linear combination of six _σ__μ_ ⊗ _τ__ν_ matrices allowed to appear in _H_0(K). On the other hand, the other ten _σ__μ_ ⊗ _τ__ν_ matrices, which correspond to

_i__γ__m__γ__n_ (1 ≤ _m_ < _n_ ≤ 5), constitute the odd-parity pairing potential. Then, we obtain a general form of Δ(K) as $$\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}}) = \, {{{\Delta

}}}_{1}\left[\mathop{\sum}\limits_{\nu =0,{x}_{i},{z}_{i}}{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{\nu }{\sigma }_{0}\otimes {\tau }_{\nu

}+{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}\otimes {\tau }_{{y}_{i}}\right]\\ +\,{{{\Delta }}}_{2}\left[\mathop{\sum}\limits_{\nu

=0,{x}_{i},{z}_{i}}{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{\nu }\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}\otimes {\tau }_{\nu }+{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}{\sigma

}_{0}\otimes {\tau }_{{y}_{i}}\right],$$ (19) where \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{\nu }\) and \({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{\nu }\) are real-valued coefficients. Note

that Δ1 and Δ2 are complex valued since \(\hat{{{\Delta }}}({{{{{{{\bf{k}}}}}}}})\ne {\hat{{{\Delta }}}}^{{{{\dagger}}} }({{{{{{{\bf{k}}}}}}}})\) in \({{{{{{{\mathcal{T}}}}}}}}\)-symmetry

breaking superconducting phases. From Eq. (19), we obtain Eq. (3) as a general form of Δ(K) in two-band models. From Eqs. (15) and (19), we obtain

$${{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})]= \,\, 8{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* })\times \left[({\psi

}_{{{{{{{{\bf{k}}}}}}}}}^{{z}_{i}}{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}-{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}\cdot

{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{z}_{i}}){f}_{{{{{{{{\bf{k}}}}}}}}}\right.\\ +\,({\psi

}_{{{{{{{{\bf{k}}}}}}}}}^{{x}_{i}}{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{z}_{i}}-{\psi

}_{{{{{{{{\bf{k}}}}}}}}}^{{z}_{i}}{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{x}_{i}}-{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}\times

{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{0})\cdot {{{{{{{{\bf{g}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\\ +\left.\,({{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}\cdot

{{{{{{{{\bf{d}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{x}_{i}}-{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{x}_{i}}{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}){h}_{{{{{{{{\bf{k}}}}}}}}}\right].$$ (20) Then, in

the _σ__μ_ ⊗ _τ__ν_ basis, the necessary conditions for the asymmetric BS (i.e., \({{{{{{{\rm{Tr}}}}}}}}[{M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}}){\tilde{H}}_{0}({{{{{{{\bf{k}}}}}}}})] \, \ne \,

0\)) can be summarized as shown in Table 3. For example, the condition (I) means that the asymmetric BS appears when \({{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* }) \, \ne

\, 0\) and \({\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{z}_{i}}{\psi }_{{{{{{{{\bf{k}}}}}}}}}^{{y}_{i}}{f}_{{{{{{{{\bf{k}}}}}}}}} \, \ne \, 0\). ASYMMETRY OF BS IN THE MINIMAL TWO-BAND MODEL We here

prove that Eq. (8) indeed expresses the asymmetric BS. For _r_ = 1, Eq. (8) leads to $${E}_{{{{{{{{\bf{k}}}}}}}}}^{\pm } = \sqrt{{\xi }_{{{{{{{{\bf{k}}}}}}}}}^{2}+| {{{\Delta }}}_{1}{\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{b}{| }^{2}+| {{{\Delta }}}_{2}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}{| }^{2}\pm 2{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* }){\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{b}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}} \pm {\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a}.$$ (21) Then, we need to specify the K-parity of \({\epsilon

}_{{{{{{{{\bf{k}}}}}}}}}^{a}\), \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{b}\), and \({\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}\), which depend on the details of the extra DOF, to investigate the property

of the BS \({E}_{-{{{{{{{\bf{k}}}}}}}}}^{\pm }\). We here denote \({\epsilon }_{-{{{{{{{\bf{k}}}}}}}}}^{a}={p}_{a}{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a}\), \({\eta

}_{-{{{{{{{\bf{k}}}}}}}}}^{b}={p}_{b}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{b}\), and \({\eta }_{-{{{{{{{\bf{k}}}}}}}}}^{ab}={p}_{ab}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}\) (_p__a_, _p__b_, _p__a__b_

 = ± 1). From Eqs. (13) and (14), we obtain \({p}_{a}{\gamma }_{a}={U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }{\gamma }_{a}^{*

}{U}_{{{{{{{{\rm{T}}}}}}}}}={U}_{{{{{{{{\rm{P}}}}}}}}}^{{{{\dagger}}} }{\gamma }_{a}{U}_{{{{{{{{\rm{P}}}}}}}}}\). On the other hand, the

\({{{{{{{\mathcal{P}}}}}}}},{{{{{{{\mathcal{T}}}}}}}}\)-odd behavior of \({M}_{-}^{(1)}({{{{{{{\bf{k}}}}}}}})=2{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* }){\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{b}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}{\gamma }_{a}\) leads to \(-{p}_{b}{p}_{ab}{\gamma }_{a}={U}_{{{{{{{{\rm{T}}}}}}}}}^{{{{\dagger}}} }{\gamma }_{a}^{*

}{U}_{{{{{{{{\rm{T}}}}}}}}}={U}_{{{{{{{{\rm{P}}}}}}}}}^{{{{\dagger}}} }{\gamma }_{a}{U}_{{{{{{{{\rm{P}}}}}}}}}\). Thus, _p__a_ = − _p__b__p__a__b_ holds in general. Using this relation, we

obtain $${E}_{-{{{{{{{\bf{k}}}}}}}}}^{\pm } = \sqrt{{\xi }_{{{{{{{{\bf{k}}}}}}}}}^{2}+| {{{\Delta }}}_{1}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{b}{| }^{2}+| {{{\Delta }}}_{2}{\eta

}_{{{{{{{{\bf{k}}}}}}}}}^{ab}{| }^{2}\mp {p}_{a}2{{{{{{{\rm{Im}}}}}}}}({{{\Delta }}}_{1}{{{\Delta }}}_{2}^{* }){\eta }_{{{{{{{{\bf{k}}}}}}}}}^{b}{\eta }_{{{{{{{{\bf{k}}}}}}}}}^{ab}} \pm

{p}_{a}{\epsilon }_{{{{{{{{\bf{k}}}}}}}}}^{a},$$ (22) where \({p}_{a}=\pm 1\). Comparing Eq. (22) with (21), we can safely say that \({E}_{-{{{{{{{\bf{k}}}}}}}}}^{\pm }\ne

{E}_{{{{{{{{\bf{k}}}}}}}}}^{+},{E}_{{{{{{{{\bf{k}}}}}}}}}^{-}\) and the BS is asymmetric. In the same manner, we can prove the asymmetry of Eq. (8) for _r_ = 0. DATA AVAILABILITY The data

that support the findings of this study are available from the corresponding author upon reasonable request. CODE AVAILABILITY The codes used for the numerical calculations in this study are

available from the corresponding author upon reasonable request. REFERENCES * Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. _Rev. Mod. Phys._ 63,

239–311 (1991). Article  ADS  Google Scholar  * Leggett, A. J. A theoretical description of the new phases of liquid 3He. _Rev. Mod. Phys._ 47, 331–414 (1975). Article  ADS  Google Scholar 

* Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. _Rev. Mod. Phys._ 82, 3045–3067 (2010). Article  ADS  Google Scholar  * Qi, Xiao-g & Zhang, Shou-Cheng Topological

insulators and superconductors. _Rev. Mod. Phys._ 83, 1057–1110 (2011). Article  ADS  Google Scholar  * Taylor, E. & Kallin, C. Intrinsic hall effect in a multiband chiral superconductor

in the absence of an external magnetic field. _Phys. Rev. Lett._ 108, 157001 (2012). Article  ADS  Google Scholar  * Bauer, E. & Sigrist, M. eds., _Noncentrosymmetric Superconductor:

Introduction and Overview_ (Springer, Berlin, 2012). * Smidman, M., Salamon, M. B., Yuan, H. Q. & Agterberg, D. F. Superconductivity and spin–orbit coupling in non-centrosymmetric

materials: a review. _Rep. Prog. Phys._ 80, 036501 (2017). Article  ADS  Google Scholar  * Wu, C. & Hirsch, J. E. Mixed triplet and singlet pairing in ultracold multicomponent fermion

systems with dipolar interactions. _Phys. Rev. B_ 81, 020508(R) (2010). Article  ADS  Google Scholar  * Hong, Zhou, L., Yi, W. & Cui, X. L. Fermion superfluid with hybridized _s_- and

_p_-wave pairings. _Sci. China Phys. Mech. Astron._ 60, 127011 (2017). Article  Google Scholar  * Fu, L. Parity-breaking phases of spin-orbit-coupled metals with gyrotropic, ferroelectric,

and multipolar orders. _Phys. Rev. Lett._ 115, 026401 (2015). Article  ADS  Google Scholar  * Kozii, V. & Fu, L. Odd-parity superconductivity in the vicinity of inversion symmetry

breaking in spin-orbit-coupled systems. _Phys. Rev. Lett._ 115, 207002 (2015). Article  ADS  Google Scholar  * Sumita, S. & Yanase, Y. Superconductivity induced by fluctuations of

momentum-based multipoles. _Phys. Rev. Res._ 2, 033225 (2020). Article  Google Scholar  * Hiroi, Z., Yamaura, J., Kobayashi, T. C., Matsubayashi, Y. & Hirai, D. Pyrochlore oxide

superconductor Cd2Re2O7 revisited. _J. Phys. Soc. Jpn._ 87, 024702 (2018). Article  ADS  Google Scholar  * Schumann, T. et al. Possible signatures of mixed-parity superconductivity in doped

polar SrTiO3 films. _Phys. Rev. B_ 101, 100503(R) (2020). Article  ADS  Google Scholar  * Wang, Y. & Fu, L. Topological phase transitions in multicomponent superconductors. _Phys. Rev.

Lett._ 119, 187003 (2017). Article  ADS  Google Scholar  * Yang, W., Xu, C. & Wu, C. Single branch of chiral Majorana modes from doubly degenerate Fermi surfaces. _Phys. Rev. Res._ 2,

042047(R) (2020). Article  Google Scholar  * Sergienko, I. A. Mixed-parity superconductivity in centrosymmetric crystals. _Phys. Rev. B_ 69, 174502 (2004). Article  ADS  Google Scholar  *

Ryu, S., Moore, J. E. & Ludwig, A. W. W. Electromagnetic and gravitational responses and anomalies in topological insulators and superconductors. _Phys. Rev. B_ 85, 045104 (2012).

Article  ADS  Google Scholar  * Qi, X.-g, Witten, E. & Zhang, S.-C. Axion topological field theory of topological superconductors. _Phys. Rev. B_ 87, 134519 (2013). Article  ADS  Google

Scholar  * Goswami, P. & Roy, B. Axionic superconductivity in three-dimensional doped narrow-gap semiconductors. _Phys. Rev. B_ 90, 041301(R) (2014). Article  ADS  Google Scholar  *

Shiozaki, K. & Fujimoto, S. Dynamical axion in topological superconductors and superfluids. _Phys. Rev. B_ 89, 054506 (2014). Article  ADS  Google Scholar  * Roy, B. H.-order topological

superconductors in \({{{{{{{\mathcal{P}}}}}}}}\)-, \({{{{{{{\mathcal{P}}}}}}}}\)-odd quadrupolar Dirac materials. _Phys. Rev. B_ 101, 220506(R) (2020). Article  ADS  Google Scholar  * Xu,

C. and Yang, W., Axion electrodynamics in _p_+_is_ superconductors. https://arxiv.org/abs/2009.12998 (2020). * Scaffidi, T., Degeneracy between even-and odd-parity superconductivity in the

quasi-1D Hubbard model and implications for Sr2RuO4. https://arxiv.org/abs/2007.13769 (2020). * Ishizuka, J. & Yanase, Y. Periodic Anderson model for magnetism and superconductivity in

UTe2. _Phys. Rev. B_ 103, 094504 (2021). Article  ADS  Google Scholar  * Braithwaite, D. et al. Multiple superconducting phases in a nearly ferromagnetic system. _Commun. Phys._ 2, 1–6

(2019). Article  Google Scholar  * Ran, S. et al. Enhancement and reentrance of spin triplet superconductivity in UTe2 under pressure. _Phys. Rev. B_ 101, 140503(R) (2020). Article  ADS 

Google Scholar  * Lin, W. C. et al. Tuning magnetic confinement of spin-triplet superconductivity. _npj Quantum Mater._ 5, 1–6 (2020). Article  ADS  Google Scholar  * Knebel, G. et al.

Anisotropy of the upper critical field in the heavy-fermion superconductor UTe2 under pressure. _J. Phys. Soc. Jpn._ 89, 053707 (2020). Article  ADS  Google Scholar  * Aoki, D. et al.

Multiple superconducting phases and unusual enhancement of the upper critical field in UTe2. _J. Phys. Soc. Jpn._ 89, 053705 (2020). Article  ADS  Google Scholar  * Thomas, S. M. et al.

Evidence for a pressure-induced antiferromagnetic quantum critical point in intermediate-valence UTe2. _Sci. Adv._ 6, eabc8709 (2020). Article  ADS  Google Scholar  * Thomas, S. M. et al.

Spatially inhomogeneous superconductivity in UTe2. _Phys. Rev. B_ 104, 224501 (2021). Article  ADS  Google Scholar  * Aoki, D. et al. Field-induced superconductivity near the superconducting

critical pressure in UTe2. _J. Phys. Soc. Jpn._ 90, 074705 (2021). Article  ADS  Google Scholar  * Black-Schaffer, A. M. & Balatsky, A. V. Odd-frequency superconducting pairing in

multiband superconductors. _Phys. Rev. B_ 88, 104514 (2013). Article  ADS  Google Scholar  * Wang, Z., Berlinsky, J., Zwicknagl, G. & Kallin, C. Intrinsic ac anomalous Hall effect of

nonsymmorphic chiral superconductors with an application to UPt3. _Phys. Rev. B_ 96, 174511 (2017). Article  ADS  Google Scholar  * Brydon, P. M. R., Abergel, D. S. L., Agterberg, D. F.

& Yakovenko, V. M. Loop currents and anomalous hall effect from time-reversal symmetry-breaking superconductivity on the honeycomb lattice. _Phys. Rev. X_ 9, 031025 (2019). Google

Scholar  * Denys, M. D. E. & Brydon, P. M. R. Origin of the anomalous Hall effect in two-band chiral superconductors. _Phys. Rev. B_ 103, 094503 (2021). Article  ADS  Google Scholar  *

Triola, C. & Black-Schaffer, A. M. Odd-frequency pairing and Kerr effect in the heavy-fermion superconductor UPt3. _Phys. Rev. B_ 97, 064505 (2018). Article  ADS  Google Scholar  *

Agterberg, D. F., Brydon, P. M. R. & Timm, C. Bogoliubov fermi surfaces in superconductors with broken time-reversal symmetry. _Phys. Rev. Lett._ 118, 127001 (2017). Article  ADS 

MathSciNet  Google Scholar  * Brydon, P. M. R., Agterberg, D. F., Menke, H. & Timm, C. Bogoliubov Fermi surfaces: General theory, magnetic order, and topology. _Phys. Rev. B_ 98, 224509

(2018). Article  ADS  Google Scholar  * Fulde, P. & Ferrell, R. A. Superconductivity in a strong spin-exchange field. _Phys. Rev._ 135, A550–A563 (1964). Article  ADS  Google Scholar  *

Larkin, A. I. & Ovchinnikov, Y. N. Inhomogeneous state of superconductors. _Zh. Eksp. Teor. Fiz._ 47, 1136 (1964). [translation: Sov. Phys. JETP 20, 762 (1965)]. * Mineev, V. P. &

Samokhin, K. V. Nonuniform states in noncentrosymmetric superconductors: Derivation of Lifshitz invariants from microscopic theory. _Phys. Rev. B_ 78, 144503 (2008). Article  ADS  Google

Scholar  * Spaldin, N. A., Fiebig, M. & Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. _J. Phys.: Condens. Matter_ 20,

434203 (2008). ADS  Google Scholar  * Flambaum, V. V., Khriplovich, I. B. & Sushkov, O. P. Nuclear anapole moments. _Phys. Lett. B_ 146, 367–369 (1984). Article  ADS  Google Scholar  *

Jeong, J., Sidis, Y., Louat, A., Brouet, V. & Bourges, P. Time-reversal symmetry breaking hidden order in Sr2(Ir,Rh)O4. _Nat. Commun._ 8, 15119 (2017). Article  ADS  Google Scholar  *

Murayama, H. et al. Bond directional anapole order in a spin-orbit coupled mott insulator Sr2(Ir1−_x_Rh_x_)O4. _Phys. Rev. X_ 11, 011021 (2021). Google Scholar  * Watanabe, H. & Yanase,

Y. Chiral photocurrent in parity-violating magnet and enhanced response in topological antiferromagnet. _Phys. Rev. X_ 11, 011001 (2021). Google Scholar  * Ahn, J., Guo, G.-Y. & Nagaosa,

N. Low-frequency divergence and quantum geometry of the bulk photovoltaic effect in topological semimetals. _Phys. Rev. X_ 10, 041041 (2020). Google Scholar  * Agterberg, D. F. & Kaur,

R. P. Magnetic-field-induced helical and stripe phases in Rashba superconductors. _Phys. Rev. B_ 75, 064511 (2007). Article  ADS  Google Scholar  * Sumita, S. & Yanase, Y.

Superconductivity in magnetic multipole states. _Phys. Rev. B_ 93, 224507 (2016). Article  ADS  Google Scholar  * Sumita, S., Nomoto, T. & Yanase, Y. Multipole superconductivity in

nonsymmorphic Sr2IrO4. _Phys. Rev. Lett._ 119, 027001 (2017). Article  ADS  Google Scholar  * Timm, C., Brydon, P. M. R. & Agterberg, D. F. Distortional weak-coupling instability of

Bogoliubov Fermi surfaces. _Phys. Rev. B_ 103, 024521 (2021). Article  ADS  Google Scholar  * Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. _Science_ 365, 684–687

(2019). Article  ADS  Google Scholar  * Jiao, L. et al. Chiral superconductivity in heavy-fermion metal UTe2. _Nature_ 579, 523–527 (2020). Article  ADS  Google Scholar  * Hayes, I. M. et

al. Weyl superconductivity in UTe2. https://arxiv.org/abs/2002.02539 (2020). * Ishihara, K. et al. Chiral superconductivity in UTe2 probed by anisotropic low-energy excitations.

https://arxiv.org/abs/2105.13721 (2021). * Hayes, I. M. et al. Multicomponent superconducting order parameter in UTe2. _Science_ 373, 797–801 (2021). Article  ADS  Google Scholar  * Yanase,

Y. Magneto-electric effect in three-dimensional coupled zigzag chains. _J. Phys. Soc. Jpn._ 83, 014703 (2014). Article  ADS  Google Scholar  * Hayami, S., Kusunose, H. & Motome, Y.

Toroidal order in metals without local inversion symmetry. _Phys. Rev. B_ 90, 024432 (2014). Article  ADS  Google Scholar  * A. Rikken, G. L. J., Fölling, J. & Wyder, P. Electrical

magnetochiral anisotropy. _Phys. Rev. Lett._ 87, 236602 (2001). Article  ADS  Google Scholar  * Watanabe, H. & Yanase, Y. Magnetic hexadecapole order and magnetopiezoelectric metal state

in BA1−_x_K_x_MN2AS2. _Phys. Rev. B_ 96, 064432 (2017). Article  ADS  Google Scholar  * Shiomi, Y. et al. Observation of a magnetopiezoelectric effect in the antiferromagnetic metal

EuMnBi2. _Phys. Rev. Lett._ 122, 127207 (2019). Article  ADS  Google Scholar  * Ramires, A. & Sigrist, M. Identifying detrimental effects for multiorbital superconductivity: application

to Sr2RuO4. _Phys. Rev. B_ 94, 104501 (2016). Article  ADS  Google Scholar  * Ramires, A., Agterberg, D. F. & Sigrist, M. Tailoring _T__c_ by symmetry principles: The concept of

superconducting fitness. _Phys. Rev. B_ 98, 024501 (2018). Article  ADS  Google Scholar  * Aoki, D. et al. Unconventional superconductivity in heavy fermion UTe2. _J. Phys. Soc. Jpn._ 88,

043702 (2019). Article  ADS  Google Scholar  * Tokunaga, Y. et al. 125Te-NMR study on a single crystal of heavy fermion superconductor UTe2. _J. Phys. Soc. Jpn._ 88, 073701 (2019). Article 

ADS  Google Scholar  * Sundar, S. et al. Coexistence of ferromagnetic fluctuations and superconductivity in the actinide superconductor UTe2. _Phys. Rev. B_ 100, 140502(R) (2019). Article 

ADS  Google Scholar  * Knebel, G. et al. Field-reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2. _J. Phys. Soc. Jpn._ 88, 063707

(2019). Article  ADS  Google Scholar  * Knafo, W. et al. Magnetic-field-induced phenomena in the paramagnetic superconductor UTe2. _J. Phys. Soc. Jpn._ 88, 063705 (2019). Article  ADS 

Google Scholar  * Miyake, A. et al. Metamagnetic transition in heavy fermion superconductor UTe2. _J. Phys. Soc. Jpn._ 88, 063706 (2019). Article  ADS  Google Scholar  * Imajo, S. et al.

Thermodynamic investigation of metamagnetism in pulsed high magnetic fields on heavy fermion superconductor UTe2. _J. Phys. Soc. Jpn._ 88, 083705 (2019). Article  ADS  Google Scholar  *

Nakamine, G. et al. Superconducting properties of heavy fermion UTe2 revealed by 125Te-nuclear magnetic resonance. _J. Phys. Soc. Jpn._ 88, 113703 (2019). Article  ADS  Google Scholar  *

Ran, S. et al. Extreme magnetic field-boosted superconductivity. _Nat. Phys._ 15, 1250–1254 (2019). Article  Google Scholar  * Bae, S. et al. Anomalous normal fluid response in a chiral

superconductor UTe2. _Nat. Commun._ 12, 1–5 (2021). Article  Google Scholar  * Kittaka, S. et al. Orientation of point nodes and nonunitary triplet pairing tuned by the easy-axis

magnetization in UTe2. _Phys. Rev. Res._ 2, 032014(R) (2020). Article  Google Scholar  * Metz, T. et al. Point-node gap structure of the spin-triplet superconductor UTe2. _Phys. Rev. B_ 100,

220504(R) (2019). Article  ADS  Google Scholar  * Nakamine, G. et al. Anisotropic response of spin susceptibility in the superconducting state of UTe2 probed with 125Te − NMR measurement.

_Phys. Rev. B_ 103, L100503 (2021). Article  ADS  Google Scholar  * Paulsen, C. et al. Anomalous anisotropy of the lower critical field and Meissner effect in UTe2. _Phys. Rev. B_ 103,

L180501 (2021). Article  ADS  Google Scholar  * Ishizuka, J., Sumita, S., Daido, A. & Yanase, Y. Insulator-metal transition and topological superconductivity in UTe2 from a

first-principles calculation. _Phys. Rev. Lett._ 123, 217001 (2019). Article  ADS  Google Scholar  * Xu, Y., Sheng, Y. & Yang, Y.-F. Quasi-two-dimensional fermi surfaces and unitary

spin-triplet pairing in the heavy fermion superconductor UTe2. _Phys. Rev. Lett._ 123, 217002 (2019). Article  ADS  Google Scholar  * Miao, L. et al. Low energy band structure and symmetries

of UTe2 from angle-resolved photoemission spectroscopy. _Phys. Rev. Lett._ 124, 076401 (2020). Article  ADS  Google Scholar  * Fujimori, S. et al. Electronic structure of UTe2 studied by

photoelectron spectroscopy. _J. Phys. Soc. Jpn._ 88, 103701 (2019). Article  ADS  Google Scholar  * Niu, Q. et al. Fermi-surface instability in the heavy-fermion superconductor UTe2. _Phys.

Rev. Lett._ 124, 086601 (2020). Article  ADS  Google Scholar  * Shick, A. B. & E.,Pickett, W. Spin-orbit coupling induced degeneracy in the anisotropic unconventional superconductor

UTe2. _Phys. Rev. B_ 100, 134502 (2019). Article  ADS  Google Scholar  * Shick, A. B., Fujimori, S.-i & Pickett, W. E. UTe2: a nearly insulating half-filled \(j=\frac{5}{2}5{f}^{3}\)

heavy-fermion metal. _Phys. Rev. B_ 103, 125136 (2021). Article  ADS  Google Scholar  * Hiranuma, K. & Fujimoto, S. Paramagnetic effects of _j_-electron superconductivity and application

to UTe2. _J. Phys. Soc. Jpn._ 90, 034707 (2021). Article  ADS  Google Scholar  * Shishidou, T., Gyeol, Suh, H., Brydon, P. M. R., Weinert, M. & Agterberg, D. F. Topological band and

superconductivity in UTe2. _Phys. Rev. B_ 103, 104504 (2021). Article  ADS  Google Scholar  * Fischer, M. H., Loder, F. & Sigrist, M. Superconductivity and local noncentrosymmetricity in

crystal lattices. _Phys. Rev. B_ 84, 184533 (2011). Article  ADS  Google Scholar  * Chazono, M., Watanabe, H. & Yanase, Y. Superconducting piezoelectric effect. _Phys. Rev. B_ 105,

024509 (2022). * Watanabe, H., Daido, A. & Yanase, Y. Nonreciprocal optical response in parity-breaking superconductors. _Phys. Rev. B_ 105, 024308 (2022). * Watanabe, H., Daido, A.,

& Yanase, Y. Nonreciprocal Meissner response in parity-mixed superconductors. https://arxiv.org/abs/2109.14874 (2021). * Wadley, P. et al. Electrical switching of an antiferromagnet.

_Science_ 351, 587–590 (2016). Article  ADS  Google Scholar  * Watanabe, H. & Yanase, Y. Symmetry analysis of current-induced switching of antiferromagnets. _Phys. Rev. B_ 98, 220412(R)

(2018). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors are grateful to Jun Ishizuka, Hikaru Watanabe, and Shuntaro Sumita for helpful discussions. This work

was supported by JSPS KAKENHI (Grants No. JP18H05227, No. JP18H01178, and No. JP20H05159) and by SPIRITS 2020 of Kyoto University. S.K. is supported by a JSPS research fellowship and by JSPS

KAKENHI (Grant No. 19J22122). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Kyoto University, Kyoto, 606-8502, Japan Shota Kanasugi & Youichi Yanase * Institute

for Molecular Science, Okazaki, 444-8585, Japan Youichi Yanase Authors * Shota Kanasugi View author publications You can also search for this author inPubMed Google Scholar * Youichi Yanase

View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.K. and Y.Y. conceived the idea and initiated the project. S.K. performed the major part

of the calculations. S.K. and Y.Y. discussed the results and co-wrote the paper. CORRESPONDING AUTHORS Correspondence to Shota Kanasugi or Youichi Yanase. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Physics_ thanks Daniel Agterberg and the other, anonymous, reviewer(s) for their

contribution to the peer review of this work. Peer reviewer reports are available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE SUPPLEMENTAL INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under

a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article

are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Kanasugi, S., Yanase, Y. Anapole superconductivity from

\({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity interband pairing. _Commun Phys_ 5, 39 (2022). https://doi.org/10.1038/s42005-022-00804-7 Download citation * Received: 14 July 2021 *

Accepted: 22 December 2021 * Published: 10 February 2022 * DOI: https://doi.org/10.1038/s42005-022-00804-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read

this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative