A new simple concept for ocean colour remote sensing using parallel polarisation radiance

Ocean colour remote sensing has supported research on subjects ranging from marine ecosystems to climate change for almost 35 years. However, as the framework for ocean colour remote sensing

is based on the radiation intensity at the top-of-atmosphere (TOA), the polarisation of the radiation, which contains additional information on atmospheric and water optical properties, has

largely been neglected. In this study, we propose a new simple concept to ocean colour remote sensing that uses parallel polarisation radiance (PPR) instead of the traditional radiation

intensity. We use vector radiative transfer simulation and polarimetric satellite sensing data to demonstrate that using PPR has two significant advantages in that it effectively diminishes

the sun glint contamination and enhances the ocean colour signal at the TOA. This concept may open new doors for ocean colour remote sensing. We suggest that the next generation of ocean

colour sensors should measure PPR to enhance observational capability.

The successful launch of the Coastal Zone Colour Scanner (CZCS) in 1978 was a milestone in the history of satellite ocean colour remote sensing1. Since then, more than twenty ocean colour

satellite sensors have been launched (www.ioccg.org/sensors_ioccg.html). These sensors capture continuous global ocean colour data (e.g. chlorophyll concentration, primary production), which

provide significant benefits for research in areas such as biological oceanography2,3 and climate change studies4,5,6. According to the current framework for ocean colour remote sensing,

the satellite sensor first measures the intensity of the upward spectral radiation at the top-of-atmosphere (TOA). The varying intensities are then used to retrieve the water-leaving

radiance after atmospheric correction, leading to the further retrieval of the optically active marine components (e.g. phytoplankton, minerals and coloured dissolved organic matter)7.

However, the current framework does not consider the polarisation of light, which could be helpful in the retrieval of water properties8. Previous studies based on radiative transfer

simulations have revealed that polarisation information on the upwelling radiation at the sea surface can improve the retrieval of the suspended particulate matter9,10 and water inherent

optical properties (e.g., absorption, scattering and backscattering coefficients) in coastal waters11,12 and help in the separation of organic and inorganic particles13,14,15. In addition,

the polarisation information at the TOA measured by satellite and airborne sensors is consistent with radiative transfer simulations and field measurements16,17 and can be used to classify

aerosol types, thus improving the water-leaving radiance retrieval18,19,20. However, despite the many advantages of using polarisation information, none of the planned future ocean colour

missions include polarimetric ocean colour sensors (www.ioccg.org/sensors/scheduled.html), which limits the capacity to advance polarisation ocean colour remote sensing. Moreover, the past

and current polarimetric satellite optical sensors, such as the POLDER (Polarisation and Directionality of the Earth's Reflectance) sensors on the ADEOS-I (Nov 1996 – Jun 1997), ADEOS-II

(Apr 2003 – Oct 2003) and PARASOL (Dec 2004 – present) satellites, were mainly designed to measure the radiative and microphysical properties of clouds and aerosols21.

In this study, we propose a new simple concept for ocean colour satellite remote sensing using the parallel polarisation radiance (PPR) instead of the traditional radiation intensity.

Although the horizontal and vertical polarisation radiances have been widely used in microwave satellite remote sensing, they have never been used in ocean colour remote sensing. The reason

for the choice of the PPR instead of the vertical polarisation radiance (VPR) is that the sea surface reflectance of PPR is general less than that of the VPR. In addition, unlike the Stokes

vector and its polarisation components, PPR is a scalar parameter which is similar to the traditional radiation intensity and it could be easily understood and exploited by the ocean colour

community.

The upward radiation at the TOA can be fully described by the Stokes vector as follows22:

where El and Er are components of the electric vector in the meridian plane (determined by the viewing direction of the satellite and the local zenith) and in the plane perpendicular to the

meridian plane, respectively. and are the respective conjugate values of El and . It should be noted that we neglect a common multiplier in Eq. (1). I is the total radiance (i.e., the

intensity measured by the ocean colour sensor), Q is the radiance linearly polarised in the meridian plane or perpendicular to the meridian plane, U is the radiance linearly polarised in the

direction 45° to the meridian plane and V is the radiance circularly polarised. I, Q and U can be analytically deduced if a satellite sensor measures the upward radiation intensities at

three angles. Generally, V is negligible for the upward radiation at the TOA above oceans.

The Stokes vector describes electromagnetic radiation in terms of measurable quantities, including the polarisation state of the electromagnetic field. For satellite applications, we define

PPR as:

For unpolarised light, such as the incident solar radiance at the TOA, then Ip = I. Although PPR is a basic parameter in classical electromagnetic radiation theory, it has never been applied

in ocean colour remote sensing. In the following sections, we demonstrate two advantages of ocean colour remote sensing using PPR.

Sun glint is a major issue for radiation intensity based ocean colour remote sensing23. In most cases, sun glint contaminated pixels are directly masked and excluded from the data

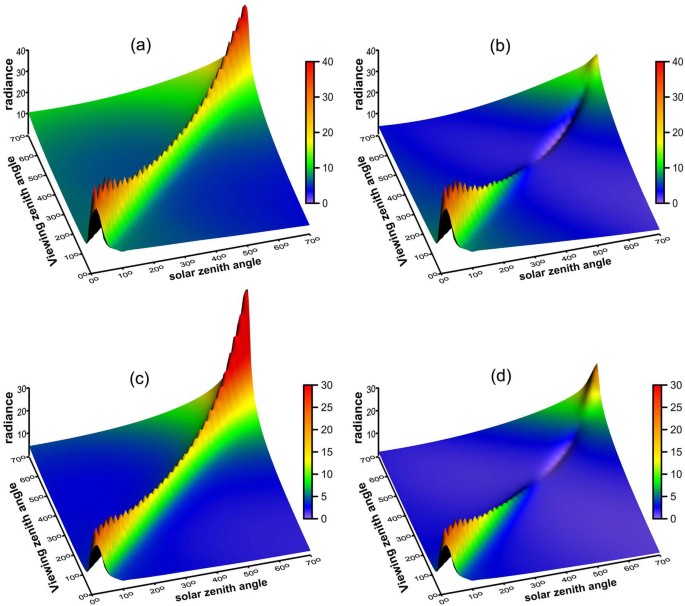
analysis24. To demonstrate the effectiveness of PPR in diminishing sun glint, we simulated the upward Stokes vector at the TOA using the vector radiative transfer model named PCOART25 (see

section Methods). The radiative transfer simulations with flat sea surface reveal that the total radiance at the TOA contains strong sun glint at the specular reflectance geometries for all

solar zenith angles (Figs. 1(a) and 1(c)). However, for the PPR at the TOA, the sun glint decreases with the solar zenith angle and disappears for solar zenith angles larger than 35° (Figs.

1(b) and 1(d)). For rough surface, we can see that the total radiance at the TOA still contains sun glint at the specular reflectance geometries for all solar zenith angles (see the

supplement Fig. S1). Yet, for the PPR at the TOA under rough surface, the sun glint decreases with solar zenith angle and disappears for solar zenith angles larger than 35°, which is similar

with the results under flat surface. Comparing to the strong sun glints along the principal plane under flat surface, sun glints are weaker and wider range of azimuth (off principal plane)

under rough surface.

The upward total radiance and PPR at the TOA simulated by PCOART.

The radiances were observed in the specular plane corresponding to the solar incident direction with units of mW/(cm2·μm·sr). The solar zenith angles were taken from 0° to 70° with a step of

1°. It should be noted that the discrete peaks (sun glint) were caused by the discrete solar zenith angles with a step of 1° and the actual sun glint should be a continuous curve. (a) The

total radiance at 443 nm, (b) PPR at 443 nm, (c) total radiance at 670 nm, (d) PPR at 670 nm.

We used polarimetric remote sensing data from the POLDER sensor on the ADEOS-II satellite to further validate the ability of diminishing sun glint by PPR under real world conditions. The

POLDER on ADEOS-II could measure I, Q and U at three bands (443 nm, 670 nm and 865 nm) at 14 observing angles. Fig. 2 shows the reflectance of total radiance and PPR at 670 nm on 10 July

2003 at the 12th observing angle. It should be noted that the data for the 13th and 14th observing angles on this day are unusable. At the 12th observing angle, strong sun glint clearly

exists in the southern hemisphere in the total radiance map (Fig. 2(a)). However, the glint disappears in the map of the PPR (Fig. 2(b)) because sun glint is generally located in regions

where the solar zenith angle is larger than 35° (Fig. 2(c)). It needs to note that real polarimetric remote sensing data cover different atmosphere and ocean conditions including the

variations of aerosol type, aerosol optical thickness and rough sea surface. Therefore, the POLDER polarimetric observations fully support the results of the radiative transfer simulation.

The reflectance of the upward total radiance and PPR at 670 nm measured by POLDER at the 12th observing angles on 10 July 2003.

The reflectance is defined as R = πL/F0 cos(θ0), where L, F0 and θ0 are the total radiance (or PPR), extra-terrestrial solar irradiance and solar zenith angle, respectively. (a) Reflectance

of total radiance, (b) reflectance of PPR, (c) reflectance of total radiance with solar zenith angle larger than 35°. The maps were generated by the Microsoft Visual C++ 6.0 and Adobe

Photoshop CS softwares.

In summary, the radiative transfer simulation and satellite observations demonstrate that PPR is capable of diminishing the sun glint at solar zenith angles larger than 35°. This reduced sun

glint can improve the data availability of ocean colour remote sensing, especially for early morning and late afternoon observations by geostationary ocean colour satellite26 and for middle

to high latitude observations by polar-orbit ocean colour satellite.

The ocean colour signal for the total radiance at the TOA can be expressed as27:

where Ib is the background upward radiance at the TOA with atmosphere and pure seawater, while It is the upward radiance at the TOA with atmosphere and seawater including the ocean colour

components (e.g. chlorophyll, suspended particle matter). The first requirement of ocean colour remote sensing is that the ocean colour signal should be sensitive to the variation in the

ocean colour components and that the capacity to discern the changes in the ocean colour components increases with the sensitivity of the signal.

We normalise Eq. (4) according to Ib and then get the normalised ocean colour signal for the total radiance as:

Similarly, the normalised ocean colour signal for PPR can be expressed as:

where Ipb is the background PPR at the TOA with atmosphere and pure seawater, while Ipt is the PPR at the TOA with atmosphere and seawater including the ocean colour components. Generally,

the greater the absolute value of the normalised ocean colour signal, the more the ocean colour signal can contribute to the total signal at the TOA.

We simulated the total radiance and the PPR at the TOA for different concentrations of chlorophyll a (Chla) and suspended particulate matter (Tsm) using the PCOART radiative transfer model

(see section 4 Methods) and obtained the normalised ocean colour signals for total radiance and PPR. Here, we only show the results for the solar-viewing relative azimuth angles of 0°, 45°,

90°, 135° and 180° (corresponding to the specular plane) in Fig. 3 for Chla and Fig. 4 for Tsm. For low solar zenith angles as represented by 0°, the PPR significantly enhances the ocean

colour signal for viewing zenith angles larger than 20° as compared with the total radiance and this enhancement increases rapidly with the viewing zenith angle (Figs. 3(a) and 4(a)). For

moderate solar zenith angles as represented by 30°, the PPR continues to enhance the ocean colour signal for both Chla and Tsm, especially at the relative azimuth angles of 135° and 180°

(Figs. 3(b) and 4(b)). For large solar zenith angles as represented by 60°, the PPR enhances the ocean colour signal at relative azimuth angles of 0°, 135° and 180° under a low viewing

zenith angle, while it slightly reduces the ocean colour signal at relative azimuth angles of 45° and 90° (Figs. 3(c) and 4(c)).

Comparison of the normalised ocean colour signal for the total radiance (solid lines) and the PPR (points) at the TOA for different Chla concentrations.

RAA is the relative azimuth angle between the solar incident and sensor viewing angles. (a) Comparison for 0° solar zenith angle (same for different azimuth angles), (b) comparison for 30°

solar zenith angle, (c) comparison for 60° solar zenith angle.

In summary, PPR can enhance the ocean colour signal relative to the total radiance at the TOA, especially for large satellite viewing zenith angles under a low to moderate solar zenith

angle, which can improve the ocean colour component retrieval at the edge of the view of the ocean colour satellite.

The greatest challenge for polarimetric ocean colour remote sensing relates to the retrieval of the water-leaving radiation from the satellite measured I, Q and U, or the corresponding

atmospheric correction. The total radiance measured by the satellite sensor can be written as28:

where Ir is the Rayleigh-scattering radiance in the absence of aerosols, Ia is the aerosol scattering radiance including the interactive scattering between molecules and aerosols, Iw is the

desired water-leaving radiance and tv is the diffuse transmittance from sea surface to satellite. It should be noted that we ignore the reflectance from whitecaps and sun glint. Similarly, Q

at the TOA can be expressed as the sum of the contributions from Rayleigh scattering (Qr), aerosol scattering (Qa) and water-leaving radiation transmitted to the TOA (Qw)29, as follows:

The Rayleigh-scattering components Ir and Qr can be accurately calculated using a vector radiative transfer model (e.g., PCOART) with the knowledge of the atmospheric pressure and wind

speed28. However, the aerosol scattering is highly variable and the components Ia and Qa cannot be predicted a priori28. In the first stage, we use the method proposed by Gordon and Wang

(1994)28 to estimate the aerosol scattering PPR over open ocean. This method uses two near-infrared bands to select the appropriate aerosol models from a set of predefined candidate models

and extrapolates the aerosol scattering radiation at the near infrared wavelength to a visible light spectral regime. In addition, tv can be estimated by the determined aerosol model and the

optical thickness. Therefore, the only unknown for the retrieval of the water-leaving radiance is Qw.

Based on the simulations in section 2.3 (see section 4 Methods), we get the Qw at the TOA as:

where Qbg is the background value from the atmospheric scattering in the absence of seawater and Qt is the value from both the atmospheric and seawater scatterings. Fig. 5 shows the

percentage of the contribution of Qw to Ip at the TOA for different wavelengths (443 nm for Chla and 670 nm for Tsm), solar zenith angles, relative azimuth angles and Chla and Tsm

concentrations. The percentage is relative larger at short wavelength (443 nm) than it at long wavelength (670 nm), but generally less than 1%, indicating that it is reasonable to neglect Qw

as compared to Ip at the TOA. Actually, both the radiative transfer simulations and polarimetric remote sensing data showed that the polarized reflectance at the TOA was virtually

insensitive to biomass content over open ocean17,30. Two factors are expected to be responsible for this result, one is that the water-leaving radiation is mostly induced by underwater

multi-scattering processing, which results in low polarisation; the other is that the atmospheric scattering further reduces the polarisation of the water-leaving radiation when it transmits

from the sea surface to the TOA. It should be noted that for some specific observing geometries (mainly in the specular plane) Qw cannot be neglected, as the percentages in these cases can

be up to 3%. Previous studies have also revealed that the polarisation information of the water-leaving radiation at the sea surface at the specular plane can be helpful for the retrieval of

suspended particulate matter9,14. Here, we only focus on the retrieval of the water-leaving radiance by neglecting Qw. Therefore, the retrieval of Qw is beyond the scope of this study and

needs to be investigated in future studies.

The percentage of the contribution of Qw to Ip at the TOA for different levels of Chla and Tsm.

RAA is the relative azimuth angle between the solar incident and sensor viewing angles. (a) and (b) are the results for 30° solar zenith angle; (c) and (d) are the results for 60° solar

zenith angle.

In addition to the simulation, we used the polarimetric remote sensing data from POLDER on 10 July 2003 to validate the feasibility of using the PPR from real satellite data. Because the

POLDER sensor only has three polarisation bands, 443 nm, 670 nm and 865 nm, we were unable to apply the method proposed by Gordon and Wang (1994)28 to estimate the aerosol scattering PPR

based on the aerosol model selection and extrapolation. Similar to the traditional atmospheric correction processes, we obtained the total radiance and PPR of the aerosol scattering at 865 

nm using the assumption that water-leaving radiation can be neglected at the near-infrared wavelength over open ocean. We further assumed that the aerosol scattering is “white”, which means

that the aerosol scattering reflectance is equal for all bands31 and obtained the total radiance and PPR of the aerosol scattering at 443 nm and 670 nm. In the future, if satellites have two

or more NIR bands with polarisation observation, we can determine the aerosol models from the satellite data directly. As in the radiative transfer simulations, we neglected the Qw and

finally obtained the desired water-leaving radiances at 443 nm and 670 nm from both the total radiance and the PPR (Fig. 6 for an example at the 12th observing angle; Supplement Figs. S4–S15

for all the 12 observing angles). The normalised water-leaving radiances retrieved by the total radiance and the PPR are reasonably consistent for both 443 nm and 670 nm. In addition, the

PPR enabled the water-leaving radiance to be retrieved in the sun glint areas of the total radiance with solar zenith angles larger than 35°, which provides further evidence of the capacity

of PPR to diminish sun glint contamination. Quantitative comparison of the normalised water-leaving radiance retrieved by the total radiance and the PPR at all 12 observing angles combined

revealed correlation coefficients of 0.92 and 0.97 with standard deviations of 0.32 and 0.09 for 443 nm and 670 nm, respectively, indicating the feasibility of using PPR for ocean colour

remote sensing (Fig. 7; Supplement Figs. S16–S17 for the results for each observing angle).

Comparison of the normalised water-leaving radiance (Lwn) retrieved by the total radiance and the PPR from POLDER data on 10 July 2003 under the 12th observing angle.

The red areas are the regions masked by sun glint. (a) Lwn at 443 nm retrieved by the total radiance, (b) Lwn at 443 nm retrieved by the PPR, (c) Lwn at 670 nm retrieved by the total

radiance, (d) Lwn at 670 nm retrieved by the PPR. The maps were generated by the Microsoft Visual C++ 6.0 and Adobe Photoshop CS softwares.

Comparison of the normalised water-leaving radiance (unit of mW/(cm2·μm·sr)) retrieved by the total radiance and the PPR at the TOA from the 12 observing angles of the POLDER data on 10 July

2003.

The colour bars show the point densities. (a) Comparison at the 443 nm band, (b) comparison at the 670 nm band.

Our results from both the radiative transfer simulation and the polarimetric satellite data reveal that the use of PPR can significantly reduce the sun glint at moderate to high solar zenith

angles. Although the total radiance in sun glint regions is generally one order greater than in non-glint regions, the linear polarisation component Q is also one order larger than in the

non-glint regions but in negative value32. Therefore, the compensating effect between the total radiance and Q reduces the sun glint in the PPR.

Furthermore, the results from the radiative transfer simulations show that PPR can increase the overall ocean colour signal relative to the total radiance at moderate to high viewing zenith

angles. The reason for this result is similar to that for the reduced sun glint using PPR. The total radiance at the TOA increases with the viewing zenith angle due to the increase in the

atmospheric path length, while the water-leaving radiance transmitted to the TOA decreases due to the reduced atmosphere diffuse transmittance. Thus, the ocean colour signal generally

decreases as the viewing zenith angle increases, as revealed in Figs. 3 and 4. Yet, for the PPR at the TOA, although the total radiance increases with the viewing zenith angle, Q also

increases correspondingly but generally in negative value. As the negative value of Q slows the increase in the PPR as the viewing zenith angle increases, the PPR thus enhances the ocean

colour signal in relation to the total radiance. Of course, the advantages demonstrated in this study are only part of the merits of polarimetric observations, as it is well known that

polarimetric radiances are useful for the retrieval of aerosol optical properties18,19,33,34 and can further improve the atmospheric correction of the ocean colour remote sensing20.

In conclusion, we propose a new simple concept for ocean colour satellite remote sensing that uses parallel polarisation radiance (PPR) instead of the traditional radiation intensity. Since

PPR is a scalar parameter which is the form used by the current ocean colour remote sensing based on the radiation intensity, it could be easily understood and exploited by the ocean colour

community. Thus, our concept may open new doors for satellite ocean colour remote sensing and is potentially applicable to forthcoming satellite missions dedicated to measuring the

polarimetric properties of radiation, such as the NASA “Preparatory Aerosols, Clouds and Ecosystems” (PACE) mission and the European Space Agency (ESA) “Multi-directional, Multi-polarisation

and Multispectral” (3 MI) mission, which are scheduled for launch around 2018. However, the polarisation observations of these satellite missions are not designed for ocean colour remote

sensing. Although PACE was driven by the ocean colour community, its polarimeter instrument was designed for the observation of the aerosols and clouds. The low signal-to-noise ratio and

small number of the polarimetric bands of these sensors limit their application to polarimetric ocean colour remote sensing. Thus, we suggest that the next generation of ocean colour sensors

should measure PPR to enhance their observational capability.

We used the PCOART vector radiative transfer model to simulate the upward radiation Stokes vector at the TOA. PCOART uses the matrix-operator method to solve the vector radiative transfer in

a coupled ocean-atmosphere system and has been validated by standard radiative transfer problems in the atmosphere and ocean and by real polarimetric remote sensing data from POLDER25.

Using PCOART, we simulated the upward radiation Stokes vector at the TOA in the specular plane using the following conditions:

The atmosphere-ocean system is divided into three layers. The upper layer comprises atmospheric molecules with optical thicknesses of 0.2361 (443 nm) and 0.0872 (670 nm). The middle layer is

the maritime aerosol with 90% relative humidity and an optical thickness of 0.2 for both 443 nm and 670 nm. The bottom layer is full absorption seawater with a flat surface. The refractive

index of the seawater is 1.34 for both 443 nm and 670 nm25.

The incident solar irradiances at the TOA are 196.98 mW/(cm2·μm) (433 nm) and 159.31 mW/(cm2·μm) (670 nm).

The solar zenith angle varies from 0° to 70° with a step of 1°.

By summing the simulated total radiance and the linear polarisation component Q, we get the PPR at the TOA in the specular plane for different solar and viewing zenith angles.

It needs to note that we use a two-layer atmosphere with all molecules placed on top of the aerosols in the simulation. Based on scalar Monte Carlo simulations, Antoine and Morel (1998)35

found that the differences of total radiances at the TOA between 50-layer and two-layer atmospheres were below 0.5% on average and they concluded that the total radiances at the TOA were

safely computed by using a two-layer atmosphere for viewing zenith angle as great as 70° if the aerosols were not absorbing. Here, we further validated the rational of the two-layer

atmosphere for the simulation of the polarisation radiances by simulating the Stokes vector at the TOA with two-layer atmosphere and mixed-layer atmosphere (aerosols mixed together with

molecules), respectively (see the supplement Figs. S2–S3). Similar to the results of the total radiances founded by Antoine and Morel (1998)35, the differences of the polarisation radiances

at the TOA between these two atmospheres are quite small for viewing zenith angle less than 70°.

Using PCOART, we simulated the upward radiation Stokes vector at the TOA at solar zenith angles of 0°, 30° and 60° for pure atmosphere, pure seawater and seawater with different

concentrations of Chla and Tsm, using the following steps:

Simulate the upward radiation Stokes vectors at 443 nm and 670 nm for pure atmosphere. The atmosphere-ocean system has the same setup as that in the simulation of the sun glint.

Simulate the upward radiation Stokes vectors at 443 nm and 670 nm for pure seawater. Similar to the simulation of the sun glint, the atmosphere-ocean system is divided into three layers,

with the bottom layer consisting of pure seawater with absorption and scattering coefficients taken from Smith and Baker (1981)36.

Simulate the upward radiation Stokes vectors at 443 nm for different Chla concentrations. The atmosphere-ocean system has the same setup as the simulation of pure seawater, except the bottom

layer is a mix of pure seawater and phytoplankton (character by Chla). The Chla concentrations are taken as 0.01, 0.05, 0.1, 0.5, 1, 2.5, 5.0, 7.5, 10.0 and 30 μg/l with homogeneous

vertical distribution. The absorption and scattering coefficients of the phytoplankton are determined by the Chla concentrations according to the bio-optical models in Morel (1991)37 and

Gordon and Morel (1983)38, respectively. The scattering phase matrix of the phytoplankton (refractive index 1.05) is calculated by Mie theory with a Junge power law size distribution ranging

from 0.1 to 50 μm with a slope of −3.09. The optical thickness of the water layer is taken as 1000 to eliminate the reflective effect of the seawater bottom.

Simulate the upward radiation Stokes vectors at 670 nm for different Tsm concentrations. The setup of the atmosphere-ocean system is the same as for step (3), except the Chla is replaced by

Tsm. The Tsm concentrations are taken as 0.1, 0.5, 1, 5, 10, 25, 50, 75, 100 and 200 mg/l with homogeneous vertical distribution. The absorption and scattering coefficients of the particles

are determined by the Tsm concentration according to the bio-optical model adopted from Bowers et al. (1998)39. The scattering phase matrix of the Tsm (refractive index 1.2) is calculated by

Mie theory with a Junge power law size distribution ranging from 0.1 to 50 μm with a slope of −3.09.

We selected the 443 nm and 670 nm bands because 443 nm is highly sensitive to Chla and 670 nm is highly sensitive to Tsm9. Based on the simulated upward radiation Stokes vector, we finally

get the PPR at the TOA for different concentrations of Chla and Tsm.

This study was supported by the National Basic Research Programme (“973” Programme) of China (grant #2009CB421202), the Public Science and Technology Research Funds Projects for Ocean

Research (grant #200905012), the National Natural Science Foundation of China (grants #41322039, #41271378 and #40976110), the National Key Technology Support Program of China (grant

#2013BAD13B01 and #2012BAH32B01) and the “Global Change and Air-Sea Interaction” project of China. We thank the French space agency Centre National d'Etudes Spatiales (CNES) for providing

the POLDER data.

State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou, China

Institute of Remote Sensing and Earth Sciences, Hangzhou Normal University, Hangzhou, China

Department of Ocean Science and Engineering, Zhejiang University, Hangzhou, China

X.H. performed the radiative transfer simulations, designed the algorithm and wrote the manuscript. D.P. designed the algorithm. Y.B. analyzed the data and wrote the manuscript. D.W.

processed the satellite data. Z.H. analyzed the data.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit

http://creativecommons.org/licenses/by-nc-nd/3.0/

Anyone you share the following link with will be able to read this content: