Hierarchies of hofstadter butterflies in 2d covalent organic frameworks

ABSTRACT The Hofstadter butterfly is one of the first and most fascinating examples of the fractal and self-similar quantum nature of free electrons in a lattice pierced by a perpendicular

magnetic field. However, the direct experimental verification of this effect on single-layer materials is still missing as very strong and inaccessible magnetic fields are necessary. For

this reason, its indirect experimental verification has only been realized in artificial periodic 2D systems, like moiré lattices. The only recently synthesized 2D covalent organic

frameworks might circumvent this limitation: Due to their large pore structures, magnetic fields needed to detect most features of the Hofstadter butterfly are indeed accessible with today

technology. This work opens the door to make this exotic and theoretical issue from the 70s measurable and might solve the quest for the experimental verification of the Hofstadter butterfly

in single-layer materials. Moreover, the intrinsic hierarchy of different pore sizes in 2D covalent organic framework adds additional complexity and beauty to the original butterflies and

leads to a direct accessible playground for new physical observations. SIMILAR CONTENT BEING VIEWED BY OTHERS ATOMICALLY PRECISE SINGLE-CRYSTAL STRUCTURES OF ELECTRICALLY CONDUCTING 2D

METAL–ORGANIC FRAMEWORKS Article 23 November 2020 LARGE-SCALE 2D HETEROSTRUCTURES FROM HYDROGEN-BONDED ORGANIC FRAMEWORKS AND GRAPHENE WITH DISTINCT DIRAC AND FLAT BANDS Article Open access

15 July 2024 A SIMPLE AND EFFICIENT PROCESS FOR THE SYNTHESIS OF 2D CARBON NITRIDES AND RELATED MATERIALS Article Open access 18 September 2023 INTRODUCTION The quantum behavior of an

electron moving in a two-dimensional lattice exposed to a magnetic field is a fundamental problem of solid-state physics that has been studied deeply in the 70s. By plotting for the first

time the allowed energies of the electrons and varying the magnetic field, Douglas Hofstadter found the stunning form of a graph that consists of duplicates of itself, embedded infinitely

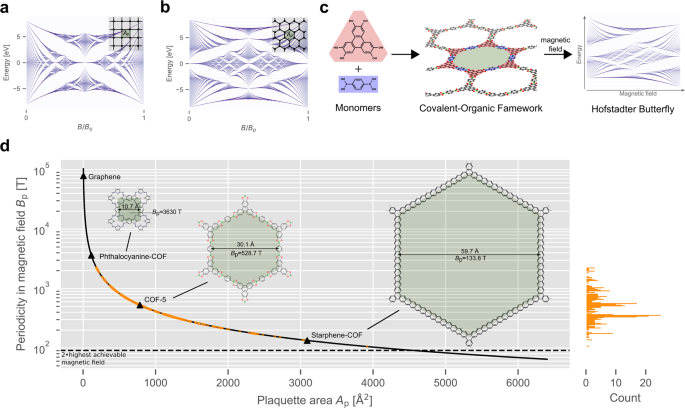
deeply, and that encodes nature in such a complex but equally self-similar manner1. This so-called Hofstadter butterfly (HB), which is shown in Fig. 1a and b, emerges from the

commensurability of the magnetic and the lattice lengths when constraining a free electron onto a lattice. This effect has fascinated theoretical physicists and mathematicians over many

decades2,3,4,5,6,7,8,9,10 and connects the mathematical concept of fractals with the world of physics by encoding the most exotic behaviors of quantum mechanics and topology, namely the

quantum Hall effect and conductance quantization in 2D materials11,12,13,14. However, the minimal magnetic field strength, _B_p, for resolving HBs depends inversely on the plaquette area

_A_p of a lattice closed loop, such as a hexagon in a honeycomb lattice, $${B}_{{{{\rm{p}}}}}=\frac{{\Phi }_{0}}{{A}_{{{{\rm{p}}}}}}.$$ (1) where, \({\Phi }_{0}=\frac{h}{2e}\) is the

magnetic flux quantum. The HB repeats itself infinitely with a period of _B_p. For graphene, for instance, _B_p is around 78 kT, making it inaccessible for experimental validation. Hence,

the HB has served since its discovery as a physical playground of mainly theoretical interest but with no direct observation. However, in the last three decades experimental verification of

the HB via artificial lattices with very large unit cells, such as moiré lattices or 2D electron gas lattices, has turned this once-theoretical issue into an active field in experimental

solid-state physics nowadays15,16,17,18,19,20,21,22,23,24,25,26. It was only the escamotage of artificial lattices, like moiré patterns, resulting in large plaquette areas which enabled the

first indirect experimental demonstration of HB through magnetotransport measurements. Two-dimensional covalent organic frameworks (2D COFs), however, have not yet been at the center of such

investigations and we can show that they indeed could be the first single-layered material to directly observe HBs. COFs are crystalline covalently bound organic polymers that have first

been successfully synthesized in 200527. The crystalline polymers are constructed from organic building block molecules attached to each other in a regular fashion which creates a periodic

and often porous structure as depicted in Fig. 1c. Due to the many available types of precursor molecules, various different structures with tunable properties are possible. As a result,

COFs have gained ever since a lot of attention in the polymer and solid-state community. Many COFs are layered materials, similar to the graphene sheets in graphite, but experimental methods

have been refined to create few-layer and indeed monolayer 2D COFs28,29,30,31,32,33,34,35. These are based on simpler lattice types, like honeycomb or hexagonal lattices, with usually very

large unit cells. This would lead to a lower magnetic field required for the experimental validation of the HB. Additionally, it has been shown how in these materials the lattice topology

itself mediates electronic and mechanical properties36,37. Moreover, recent investigations of topological effects in 2D COFs showed their potential as topological materials38,39,40,41,42,43.

All of this makes 2D COFs interesting materials for the exploration of fractality, quantum effects and finally finding a HB at experimentally viable magnetic fields. In Fig. 1d, the

dependency of _B_p on the plaquette area _A_p is depicted, including known 2D COFs with honeycomb, tetragonal or square lattice structure. This shows that several COFs already exist where

the HB can be measured to a great extent with experimentally achievable magnetic fields. We chose 91 T as comparison, which is twice the highest achievable continuous magnetic field (2 ⋅ 

45.5 T = 91 T 44), as the HB is symmetric in the magnetic field and consequently only half of its spectrum needs to be measured. Additionally, a greater complexity and a richer phenomenon of

the HB is expected due to COFs rich pore hierarchy. The HB for three different exemplary 2D COFs (shown in Fig. 1d) are calculated in the following: complex hierarchical patterns and

fractal HBs can be observed at measurable magnetic fields. RESULTS EMBEDDED HOFSTADTER BUTTERFLIES Figure 2 shows the well-known COF-5 with its three different plaquette types marked as I to

III. COF-5 is the first synthesized and one of the most studied COF which has, just like graphene, a honeycomb lattice as shown in Fig. 2b27. As the HB repeats itself with a period of _B_p,

we search for a reoccurring pattern in the calculated spectrum. In Fig. 2c, one can see such a pattern with a period of approximately 240 kT. This spectrum, however, does not resemble the

HB of an equivalent honeycomb lattice (Fig. 1b) and its period is very large. A zoom into the spectrum, as shown in Fig. 2d, indicate more complex patterns and a further zoom in Fig. 2e

reveals astonishingly a HB that is equivalent of the one of graphene, but only at 528.7 T. This corresponds to the _B_p of the lattice plaquette I according to equation (1). To avoid

confusion in the following discussion, we will call the patterns that resemble the HB of simple lattices specifically ‘HB’ and the rest of the spectrum generally ‘butterfly spectrum’. How

can we understand the formation of different patterns on the various scales of magnetic fields? As seen in Fig. 2c, the butterfly spectrum contains many different ‘bands’ that change with

the magnetic field. We will call those ‘ribbons’ to give a clear distinction to bands in band-structure plots. This complexity arises due to the numerous electronic states that COFs have

compared to simple lattices. A zoom closer to some of the ribbons in Fig. 2d, shows that each ribbon itself contains many smaller complex features that sometimes overlap and interfere with

each other and create new patterns. A comparison with the band structure in Supplementary Fig. 2 reveals that some ribbons are based on a band-structure equivalent of a simple honeycomb

lattice, while others are more similar to the one of a kagome-lattice. It is known that COF-5 has kagome-characteristic bands45. The resulting butterfly spectrum of these kagome-like bands

is similarly distorted as the one of a simple kagome-lattice HB6. Furthermore, a comparison of the band structure and HBs of all studied COFs in this manuscript is shown in Supplementary

Fig. 5. The final zoom in Fig. 2e into the isolated ribbon at around −6.9 eV shows the honeycomb HB. This shows that the lattice type itself dictates the electronic structure and topological

effects. A key difference to the HB in a simple honeycomb lattice is that HB in COF-5 is strictly speaking not repeating itself, but is distorted for higher magnetic fields due to the

superposition of different periodicities. HIERARCHICAL PATTERNS IN 2D COFS But why do we see a periodic pattern at ~240 kT in Fig. 2c for COF-5? This value does not coincide with any of the

_B_p values of the three plaquette types I to III in COF-5 labeled in Fig. 2a: the honeycomb lattice plaquette I, the benzene ring II and the boronic ester based five-membered ring III, with

periodicities _B_p of 528.7 T, 81.06 kT, and 121.9 kT, respectively. As the latter two periods have approximately a common denominator, a new periodic pattern with a bigger period at ~240

kT ( ≈ 2 ⋅ 121.9 kT ≈ 3 ⋅ 81 kT) is visible. To better understand the influence of multiple plaquette types on the butterfly spectrum, we next investigate a COF with four different

plaquettes. This COF is based on Phthalocyanine as shown in Fig. 3a and has a square lattice. It has been shown in previous studies that this COF has interesting topological properties,

although usually investigated including a metal-center40,42,43. In Fig. 3a, we depict the four different kinds of plaquettes marked as I to IV: square lattice plaquette that arises from the

fused Phthalocyanines units I, the pore inside of a Phthalocyanine unit II, the benzene ring III and the pyrole five-membered ring IV. In Fig. 3d, we can see that similar to COF-5, there is

an overlap of the periodicities of III (81.18 kT) and IV (121.6 kT) that leads to a new combined pattern with a period of ~240 kT. The spectrum shows that there are patterns with different

periods which are marked in the figure. For better visualization of the repeating patterns, a wider magnetic field range of the butterfly spectrum plotted in Supplementary Fig. 3. When

zooming into one of the ribbons in Fig. 3d, we see as expected a HB in Fig. 3c that resembles the one of a square lattice (compare to Fig. 1a), which further shows how lattice types guides

topological effects like the HB. But since the period of II is only around five times larger than I, the oscillation of II distrorts the HB in Fig. 3c. From this we can see that the closer

the scales of periodicities of different plaquettes are, the more they influence each other and the more distorted the HB is. We would like to point out that the fractality and the actual HB

is only created by the lattice plaquette, i.e. the biggest plaquette. The other plaquettes are only responsible for additional periodicity, but not for fractality, as shown in Supplementary

Fig. 4. TOWARDS A MEASURABLE HB IN 2D COFS The COFs investigated so far do not have large enough unit cells to create a periodicity _B_p that would be measurable in today’s experiments.

Hence, a COF with larger pores is required. One COF (COF-122) exists already that is close to the required unit cell size46. However, as parts of this COF have many rotational degrees of

freedom and is hence not flat, it is in our opinion not suitable for a flat monolayer material. For this reason, we propose a COF that is based on the recently reported class of Starphene

molecules which are triangular molecules of fused benzene rings47. When connected, a highly porous COF with a honeycomb lattice would result which we call Starphene-COF, as shown in Fig. 4a

and b. This theoretical COF also is a fully conjugated system which should lead to a good conductivity. In the Starphene-COF, there are only two plaquette types: the honeycomb lattice

plaquette I and the benzene-rings II. This leads to a period of 133.8 T for the lattice plaquette I and a period of approximately 78.68 kT for the benzene ring (II). The full butterfly

spectrum up to 80 kT is depicted in Fig. 4d. In Fig. 4c, we zoom in to the magnetic field range of the smaller period and see that a HB arises that looks similar to the one of a simple

honeycomb lattice in Fig. 1b. Since _B_p is only 133.8 T, the HB of the Starphene-COF would be accessible to a great extent by available magnetic fields, possibly solving the quest for

direct experimental verification of the HB in a single-layer 2D material in the future. The butterfly spectrum in Fig. 4d also has some interesting properties similar to a related class of

materials, graphene antidot lattices (GALs) which is graphene with periodic holes. In GALs, a typical graphene HB pattern still emerges, even though it becomes less distinct the bigger the

holes in the lattice becomes. The Starphene-COF can be seen as an edge case of such a GAL, in the sense of a porous graphene which has the biggest possible hole for its repeating unit.

Another feature that is known from GALs is that the band gap is being quenched with increasing magnetic field, which can be seen for the Starphene-COF at around 6 kT at 0 eV in Fig. 4d48.

During the preparation of the manuscript, a COF with a very large pore was reported49. We show in Supplementary Fig. 1 the corresponding HB that is resolved at 122.6 T, which is even lower

than our proposed Starphene-COF. This demonstrates how the rapid advances in synthesis can provide systems to experimentally measure the HB in the near future. DISCUSSION We have shown that

2D COFs are promising materials for the direct experimental verification of the Hofstadter butterfly in pure 2D materials and that there are additional hierarchical patterns that are not

present in HBs of simple lattices. This work might turn this merely-theoretical issue from the 70s into an active experimental research activity nowadays and trigger the race for the first

direct measurement. We found equivalents of simple lattice HB inside the complex and beautiful butterfly spectra of 2D COFs. Moreover, hierarchical structures and periodicities can be found

within these spectra, due to the various pore types inside a single COF-structure, opening dimensions for more physical discoveries. Furthermore, we showed that for 2D COFs with large unit

cells the magnetic field to measure a HB is small enough to be experimentally viable. 2D COFs can provide the ideal playground for the investigation of such fundamental quantum effects and

the recent advances in single-layer synthesis of 2D COFs will lead in the foreseeable future to the direct observation of the Hofstadter butterfly in a single-layer 2D material. METHODS

CALCULATION OF THE HB A tight-binding hamiltonian was constructed from the Slater-Koster parametrization which is used in Density Functional based Tight Binding. The parameters include

tabulated distance-dependent orbital-orbital interactions and respective on-site energies50. Here, the matsci parametrization with on-site energies for the angular momentum p for the given

atom and pp_π_ hopping parameters51. The hopping was assigned according to the respective distance between the atoms. To simplify the model and the energy-spectrum, only nearest neighbor

interactions were considered. With the help of the Atomic Simulation Environment (ASE) package52, the geometry and hamiltonian were imported into the pybinding code with which all further

calculations were performed53. For the geometry, only a strict 2D system was used, meaning the z-coordinates were discarded. The influence of a perpendicular magnetic field on the 2D

structure was approximated with the Peierls-substitution54: $${t}_{{{{\rm{nm}}}}}\to {t}_{{{{\rm{nm}}}}}{{{{\rm{e}}}}}^{i\frac{2\pi }{{\Phi

}_{0}}\int\nolimits_{n}^{m}{{{{\bf{A}}}}}_{nm}{{{\rm{d}}}}{{{\bf{l}}}}}$$ (2) with _t_nm as the hopping-parameter or off-diagonal elements for nearest neighbor sites _n_ and _m_, Φ0 as the

magnetic flux quantum, Anm as the magnetic vector potential with a chosen gauge of A(_x_, _y_, _z_) = (_B_y, 0, 0). The electronic density of states (DOS) for the structures with an applied

perpendicular magnetic field was calculated with the in pybinding integrated Kernel Polynomial Method (KPM). In the KPM, the DOS is calculated by reconstruction from the KPM moments which

are evaluated in a stochastic fashion55. The DOS was evaluated for a 50 × 50 supercell and 3 random vectors for the stochastic calculation of KPM moments. Sweeping through a magnetic field

range and plotting the DOS for each magnetic field, results in the shown butterfly spectra. The energy scale was centered with respect to the the minimum and maximum energy value of the

butterfly spectrum. This convention for the energy scale was chosen instead Fermi level centering because the TB model only includes pp_π_ orbitals and their occupation for more complex

systems (like the Phthalocyanine-COF or COF-5) cannot be derived directly from the TB model. OPTIMIZATION OF COF STRUCTURES The 2D COF-structures where obtained from optimization with

Density Functional based Tight Binding calculations with the code DFTB+56. The optimization was carried out at the Γ point with a maximum force component of 1e-06 of the conjugate gradient

algorithm. A tolerance of 1e-08 for the self consistent cycles was chosen. As Slater-Koster parameters, the matsci parameter set was used51. DATA AVAILABILITY The data necessary to produce

the butterfly spectrum are uploaded to https://github.com/DBodesheim/HB_pybinding upon publication. CODE AVAILABILITY The code necessary to produce the butterfly spectrum is uploaded to

https://github.com/DBodesheim/HB_pybinding upon publication. REFERENCES * Hofstadter, D. R. Energy levels and wave functions of bloch electrons in rational and irrational magnetic fields.

_Phys. Rev. B_ 14, 2239–2249 (1976). Article  CAS  Google Scholar  * Rammal, R. Landau level spectrum of bloch electrons in a honeycomb lattice. _J. Phys._ 46, 1345–1354 (1985). Article 

Google Scholar  * Gumbs, G. & Fekete, P. Hofstadter butterfly for the hexagonal lattice. _Phys. Rev. B_ 56, 3787–3791 (1997). Article  CAS  Google Scholar  * Koshino, M., Aoki, H.,

Kuroki, K., Kagoshima, S. & Osada, T. Hofstadter butterfly and integer quantum hall effect in three dimensions. _Phys. Rev. Lett._ 86, 1062–1065 (2001). Article  CAS  Google Scholar  *

Osadchy, D. & Avron, J. E. Hofstadter butterfly as quantum phase diagram. _J. Math. Phys._ 42, 5665–5671 (2001). Article  Google Scholar  * Xiao, Y., Pelletier, V., Chaikin, P. M. &

Huse, D. A. Landau levels in the case of two degenerate coupled bands:kagomé lattice tight-binding spectrum. _Phys. Rev. B_ 67, 104505 (2003). Article  Google Scholar  * Nemec, N. &

Cuniberti, G. Hofstadter butterflies of carbon nanotubes: pseudofractality of the magnetoelectronic spectrum. _Phys. Rev. B_ 74, 165411 (2006). Article  Google Scholar  * Nemec, N. &

Cuniberti, G. Hofstadter butterflies of bilayer graphene. _Phys. Rev. B_ 75, 201404 (2007). Article  Google Scholar  * Yılmaz, F. & Oktel, M. O. Hofstadter butterfly evolution in the

space of two-dimensional bravais lattices. _Phys. Rev. A_ 95, 063628 (2017). Article  Google Scholar  * Ferrari, A. C. et al. Science and technology roadmap for graphene, related

two-dimensional crystals, and hybrid systems. _Nanoscale_ 7, 4598–4810 (2015). Article  CAS  Google Scholar  * von Klitzing, K. The quantized hall effect. _Rev. Mod. Phys._ 58, 519–531

(1986). Article  Google Scholar  * Kumar, A. et al. Integer quantum hall effect in trilayer graphene. _Phys. Rev. Lett._ 107, 126806 (2011). Article  CAS  Google Scholar  * Li, L. et al.

Quantum hall effect in black phosphorus two-dimensional electron system. _Nat. Nanotechnol._ 11, 593–597 (2016). Article  CAS  Google Scholar  * Kjaergaard, M. et al. Quantized conductance

doubling and hard gap in a two-dimensional semiconductor-superconductor heterostructure. _Nat. Commun._ 7, 12841 (2016). Article  CAS  Google Scholar  * Kuhl, U. & Stöckmann, H.-J.

Microwave realization of the hofstadter butterfly. _Phys. Rev. Lett._ 80, 3232–3235 (1998). Article  CAS  Google Scholar  * Albrecht, C. et al. Evidence of hofstadter’s fractal energy

spectrum in the quantized hall conductance. _Phys. Rev. Lett._ 86, 147–150 (2001). Article  CAS  Google Scholar  * Zaric, S. et al. Optical signatures of the aharonov-bohm phase in

single-walled carbon nanotubes. _Science_ 304, 1129–1131 (2004). Article  CAS  Google Scholar  * Geisler, M. C. et al. Detection of a landau band-coupling-induced rearrangement of the

hofstadter butterfly. _Phys. Rev. Lett._ 92, 256801 (2004). Article  CAS  Google Scholar  * Ponomarenko, L. A. et al. Cloning of dirac fermions in graphene superlattices. _Nature_ 497,

594–597 (2013). Article  CAS  Google Scholar  * Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum hall effect in moiré superlattices. _Nature_ 497, 598–602 (2013). Article 

CAS  Google Scholar  * Hunt, B. et al. Massive dirac fermions and hofstadter butterfly in a van der waals heterostructure. _Science_ 340, 1427–1430 (2013). Article  CAS  Google Scholar  *

Yu, G. L. et al. Hierarchy of hofstadter states and replica quantum hall ferromagnetism in graphene superlattices. _Nat. Phys._ 10, 525–529 (2014). Article  CAS  Google Scholar  * Yang, W.

et al. Hofstadter butterfly and many-body effects in epitaxial graphene superlattice. _Nano Lett._ 16, 2387–2392 (2016). Article  CAS  Google Scholar  * Ni, X. et al. Observation of

hofstadter butterfly and topological edge states in reconfigurable quasi-periodic acoustic crystals. _Commun. Phys._ 2, 55 (2019). Article  Google Scholar  * Huber, R. et al. Gate-tunable

two-dimensional superlattices in graphene. _Nano Lett._ 20, 8046–8052 (2020). Article  CAS  Google Scholar  * Lu, X. et al. Multiple flat bands and topological hofstadter butterfly in

twisted bilayer graphene close to the second magic angle. _Proc. Natl Acad. Sci. USA_ 118, e2100006118 (2021). Article  CAS  Google Scholar  * Côté, A. P. et al. Porous, crystalline,

covalent organic frameworks. _Science_ 310, 1166–1170 (2005). Article  Google Scholar  * Dienstmaier, J. F. et al. Synthesis of well-ordered COF monolayers: surface growth of nanocrystalline

precursors versus direct on-surface polycondensation. _ACS Nano_ 5, 9737–9745 (2011). Article  CAS  Google Scholar  * Dienstmaier, J. F. et al. Isoreticular two-dimensional covalent organic

frameworks synthesized by on-surface condensation of diboronic acids. _ACS Nano_ 6, 7234–7242 (2012). Article  CAS  Google Scholar  * Colson, J. W. & Dichtel, W. R. Rationally

synthesized two-dimensional polymers. _Nat. Chem._ 5, 453–465 (2013). Article  CAS  Google Scholar  * Zhong, Y. et al. Wafer-scale synthesis of monolayer two-dimensional porphyrin polymers

for hybrid superlattices. _Science_ 366, 1379–1384 (2019). Article  CAS  Google Scholar  * Liu, K. et al. On-water surface synthesis of crystalline, few-layer two-dimensional polymers

assisted by surfactant monolayers. _Nat. Chem._ 11, 994–1000 (2019). Article  CAS  Google Scholar  * Li, Y., Chen, W., Xing, G., Jiang, D. & Chen, L. New synthetic strategies toward

covalent organic frameworks. _Chem. Soc. Rev._ 49, 2852–2868 (2020). Article  CAS  Google Scholar  * Li, X. et al. Partitioning the interlayer space of covalent organic frameworks by

embedding pseudorotaxanes in their backbones. _Nat. Chem._ 12, 1115–1122 (2020). Article  CAS  Google Scholar  * Ortega-Guerrero, A. et al. Multiscale modeling strategy of 2d covalent

organic frameworks confined at an air–water interface. _ACS Appl. Mater. Interfaces_ 13, 26411–26420 (2021). Article  CAS  Google Scholar  * Springer, M. A., Liu, T.-J., Kuc, A. & Heine,

T. Topological two-dimensional polymers. _Chem. Soc. Rev._ 49, 2007–2019 (2020). Article  CAS  Google Scholar  * Raptakis, A., Dianat, A., Croy, A. & Cuniberti, G. Predicting the bulk

modulus of single-layer covalent organic frameworks with square-lattice topology from molecular building-block properties. _Nanoscale_ 13, 1077–1085 (2021). Article  CAS  Google Scholar  *

Dong, L., Kim, Y., Er, D., Rappe, A. M. & Shenoy, V. B. Two-dimensional _π_-conjugated covalent-organic frameworks as quantum anomalous hall topological insulators. _Phys. Rev. Lett._

116, 096601 (2016). Article  Google Scholar  * Jiang, W., Ni, X. & Liu, F. Exotic topological bands and quantum states in metal–organic and covalent–organic frameworks. _Acc. Chem. Res._

54, 416–426 (2021). Article  CAS  Google Scholar  * Pham, H. Q. & Pham-Tran, N.-N. Topological insulating phase in single-layer pentagonal covalent organic frameworks: a reticular

design using metal phthalocyanine. _Chem. Mater._ 33, 4488–4499 (2021). Article  CAS  Google Scholar  * Cui, B. et al. Realization of lieb lattice in covalent-organic frameworks with tunable

topology and magnetism. _Nat. Commun._ 11, 66 (2020). Article  CAS  Google Scholar  * Li, J., Gu, L. & Wu, R. Transition-metal phthalocyanine monolayers as new chern insulators.

_Nanoscale_ 12, 3888–3893 (2020). Article  CAS  Google Scholar  * Jiang, W., Zhang, S., Wang, Z., Liu, F. & Low, T. Topological band engineering of lieb lattice in phthalocyanine-based

metal–organic frameworks. _Nano Lett._ 20, 1959–1966 (2020). Article  CAS  Google Scholar  * Hahn, S. et al. 45.5-tesla direct-current magnetic field generated with a high-temperature

superconducting magnet. _Nature_ 570, 496–499 (2019). Article  CAS  Google Scholar  * Kuc, A. et al. Proximity effect in crystalline framework materials: Stacking-induced functionality in

MOFs and COFs. _Adv. Funct. Mater._ 30, 1908004 (2020). Article  CAS  Google Scholar  * Zhao, C., Lyu, H., Ji, Z., Zhu, C. & Yaghi, O. M. Ester-linked crystalline covalent organic

frameworks. _J. Am. Chem. Soc._ 142, 14450–14454 (2020). Article  CAS  Google Scholar  * Holec, J. et al. A large starphene comprising pentacene branches. _Angew. Chem. Int. Ed._ 60,

7752–7758 (2021). Article  CAS  Google Scholar  * Pedersen, J. G. & Pedersen, T. G. Hofstadter butterflies and magnetically induced band-gap quenching in graphene antidot lattices.

_Phys. Rev. B_ 87, 235404 (2013). Article  Google Scholar  * Riaño, A. et al. An expanded 2d fused aromatic network with 90-ring hexagons. _Angew. Chem. Int. Ed._ 61, e202113657 (2021).

Google Scholar  * Slater, J. C. & Koster, G. F. Simplified lcao method for the periodic potential problem. _Phys. Rev._ 94, 1498–1524 (1954). Article  CAS  Google Scholar  * Manzano, H.

et al. Do cement nanotubes exist? _Adv. Mater._ 24, 3239–3245 (2012). Article  CAS  Google Scholar  * Larsen, A. H. et al. The atomic simulation environment—a python library for working with

atoms. _J. Phys. Condens. Matter_ 29, 273002 (2017). Article  Google Scholar  * Moldovan, D., Anđelković, M. & Peeters, F. _pybinding v0.9.5: a Python package for tight- binding

calculations_. https://doi.org/10.5281/zenodo.4010216. (2020). * Peierls, R. Zur theorie des diamagnetismus von leitungselektronen. _Z. Phys._ 80, 763–791 (1933). Article  CAS  Google

Scholar  * Weiße, A., Wellein, G., Alvermann, A. & Fehske, H. The kernel polynomial method. _Rev. Mod. Phys._ 78, 275–306 (2006). Article  Google Scholar  * Hourahine, B. et al. DFTB+, a

software package for efficient approximate density functional theory based atomistic simulations. _J. Chem. Phys._ 152, 124101 (2020). Article  CAS  Google Scholar  * Ongari, D.,

Yakutovich, A. V., Talirz, L. & Smit, B. Building a consistent and reproducible database for adsorption evaluation in covalent–organic frameworks. _ACS Cent. Sci._ 5, 1663–1675 (2019).

Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS We acknowledge financial support from the DFG project CRC-1415 (No. 417590517). We thank Antonios Raptakis for providing

the geometry-files of the COF structures. FUNDING Open Access funding enabled and organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institute for Materials Science and

Max Bergmann Center for Biomaterials, TU Dresden, Dresden, Germany David Bodesheim, Robert Biele & Gianaurelio Cuniberti * Dresden Center for Computational Materials Science (DCMS), TU

Dresden, Dresden, Germany Gianaurelio Cuniberti Authors * David Bodesheim View author publications You can also search for this author inPubMed Google Scholar * Robert Biele View author

publications You can also search for this author inPubMed Google Scholar * Gianaurelio Cuniberti View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS D.B. performed the calculations. R.B. and G.C. supervised and guided the project. All authors contributed equally to the preparation of this manuscript. CORRESPONDING AUTHOR

Correspondence to Gianaurelio Cuniberti. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIAL RIGHTS AND PERMISSIONS OPEN ACCESS This

article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as

you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party

material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s

Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Bodesheim, D., Biele, R. & Cuniberti, G.

Hierarchies of Hofstadter butterflies in 2D covalent organic frameworks. _npj 2D Mater Appl_ 7, 16 (2023). https://doi.org/10.1038/s41699-023-00378-0 Download citation * Received: 25

February 2022 * Accepted: 10 March 2023 * Published: 25 March 2023 * DOI: https://doi.org/10.1038/s41699-023-00378-0 SHARE THIS ARTICLE Anyone you share the following link with will be able

to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative