The refractive index and electronic gap of water and ice increase with increasing pressure

ABSTRACT Determining the electronic and dielectric properties of water at high pressure and temperature is an essential prerequisite to understand the physical and chemical properties of

aqueous environments under supercritical conditions, for example, in the Earth interior. However, optical measurements of compressed ice and water remain challenging, and it has been common

practice to assume that their band gap is inversely correlated with the measured refractive index, consistent with observations reported for hundreds of materials. Here we report _ab initio_

molecular dynamics and electronic structure calculations showing that both the refractive index and the electronic gap of water and ice increase with increasing pressure, at least up to 30 

GPa. Subtle electronic effects, related to the nature of interband transitions and band edge localization under pressure, are responsible for this apparently anomalous behaviour. SIMILAR

CONTENT BEING VIEWED BY OTHERS THERMODYNAMIC MECHANISM OF THE DENSITY AND COMPRESSIBILITY ANOMALIES OF WATER IN THE RANGE − 30 < _T_ (°C) < 100 Article Open access 24 January 2022

DYNAMIC COMPRESSION OF WATER TO CONDITIONS IN ICE GIANT INTERIORS Article Open access 13 January 2022 STRUCTURE AND PROPERTIES OF TWO SUPERIONIC ICE PHASES Article 14 October 2021

INTRODUCTION Water is arguably the most important material in the biosphere, as well as a key constituent of the Earth crust and mantle. Its properties have been extensively studied as a

function of temperature (T) and pressure (P) for several decades1,2. However, the electronic structure of water under pressure has remained elusive, due to experimental difficulties in

measuring absorption processes in wide band gap insulators in diamond anvil cells. The electronic properties of compressed water are key, for example, to understanding electron charge

transfer rates in redox reactions3,4 occurring in supercritical water1 and aqueous solutions in the Earth’s interior2; such reactions, which depend on both the electronic and static

dielectric constant of water, determine the oxidation states of minerals and rocks. Water was predicted to undergo an insulator-to-metal transition at rather large pressures, estimated

between 100 GPa and 5 TPa5,6,7,8, although no experimental confirmation has yet been reported. Experimentally, it is difficult to directly establish the variation of the liquid electronic

gap as a function of P, which at ambient conditions is outside the optical window of diamond: the optical gap of diamond is 5.4 eV (ref. 9) with the absorption tail as low as ~4 eV, and the

quasi particle gap of water at ambient conditions is estimated to be 8.7±0.5 eV (refs 10, 11) with the optical absorption onset at ~7 eV (refs 12, 13). Hence, the band gap (_E_g) of high

pressure ice (a disordered ice phase stable between 3 and ~60 GPa (refs 14, 15)) has been inferred from measurements of its refractive index, _n_, which can be obtained by using low energy

photons without probing absorption processes16. In particular, it has been common practice to use a single-oscillator model, for example, the Penn model17, to relate _n_ and _E_g, as in the

case of other molecular crystals, notably hydrogen18,19. According to the Penn model, the refractive index _n_ and the electronic gap _E_g are inversely correlated: , where _ω_fp is the

plasma frequency. This inverse correlation between _n_ and _E_g holds for a broad class of materials20,21. Zha _et al._16 measured the refractive index of ice VII as a function of pressure

up to 120 GPa and found that it increased with pressure, similar to the case of solid hydrogen. They found weak dispersion of the refractive index, and its pressure dependence, leading them

to conclude that the band gap is preserved to very high pressure, ultimately closing only in the terapascal pressures and well beyond the stability field of ice VII. The refractive index of

liquid water has been measured only up to 7 GPa, at T=673 K (ref. 22), while no measurements have yet been reported of its electronic gap in such P-T regime. Here we report _ab initio_

molecular dynamics (MD) simulations of water under pressure and calculations of the refractive index _n_ and the electronic gap _E_g in the pressure range 0–30 GPa. The values obtained for

the refractive index of ice and water are in good agreement with experiments16,22; however, we find that both _n_ and _E_g increase with increasing pressure in the solid and liquid phases.

Our results show that a single-oscillator model used to rationalize the electronic properties of many semiconductors and insulators may not be employed to describe water under pressure. We

find that, because of subtle but important changes in the localization properties of the valence band edge of water and ice, the strength of inter band transitions depends on pressure. As a

consequence _n_ and _E_g are not inversely correlated, but exhibit a more complex interdependence, not captured by widely used simple models. Our results are consistent with those of Hermann

and Schwerdtfeger23 who reported an increase of the optical gap of ice under pressure, using calculations based on many body perturbation theory with a fitted dielectric constant. RESULTS

REFRACTIVE INDEX OF WATER AND ICE For photon energies (ℏω) much smaller than the band gap, absorption processes may be ignored and , where 1 is the real part of the electronic dielectric

constant. For simple semiconductors, the Penn model17 yields a reasonable approximation of 1. The validity of such model may extend beyond simple semiconductors, as suggested by Wemple and

DiDomenico20 who showed that [1(0)−1] is approximately proportional to 1/_E_g for more than 100 solids and liquids. However, as discussed below, the description of the properties of water

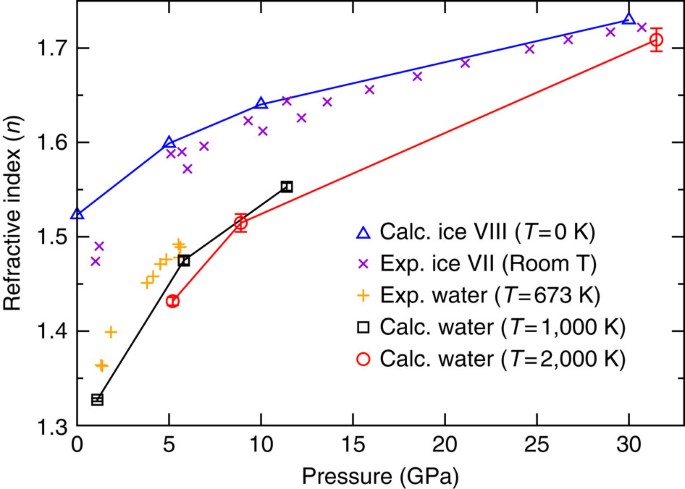
and ice requires a more sophisticated level of theory. Figure 1 reports the calculated refractive index of water and ice, as a function of pressure, and shows that _n_ increases with

increasing P along isotherms for both the solid and the liquid. We also show experimental results for ice VII (ref. 16) and water up to 7 GPa (ref. 22). To the best of our knowledge, our

results represent the first data obtained for the refractive index of the supercritical liquid above 7 GPa. Indeed, the highly corrosive character of hot, compressed water makes experiments

rather challenging at high P and T. We find good agreement with experiments, especially above 5 GPa, with the deviations present at low pressure ascribed to errors introduced by the use of

the Perdew-Burke-Ernzerhof (PBE) functional24. Semi-local functionals have been shown to yield results for water and ice under pressure in better agreement with experiments than at ambient

conditions25, for example, for the calculation of the equation of state26 and the dielectric properties15,26. Preliminary calculations of the electronic dielectric constant of water at

ambient conditions using the PBE0 (refs 27, 28) functional showed a much improved agreement with experiment, yielding 1=1.78 (to be compared with the experimental value of 1.77). The same

improvement was also found for the static dielectric constant of ice Ih29. For ice VIII at 30 GPa, we find instead a minor difference of 4% between the electronic dielectric constants

obtained by PBE and PBE0. ELECTRONIC GAP OF WATER AND ICE In Fig. 2, we show the electronic gap of water and ice, computed as the difference between the single particle energies of the

conduction band minimum (CBM) and the valence band maximum (VBM) as a function of pressure. We report values obtained with the PBE functional and, in the inset, with the hybrid functional,

PBE0 (refs 27, 28). In spite of large statistical fluctuations at high T, the trend of an increasing gap with pressure is evident, irrespective of the level of theory used. As well known,

the PBE functional underestimates the band gap of water11,30, but the gap variation under pressure is qualitatively the same and quantitatively similar within PBE and PBE0. We expect the

rate at which the optical gap increases with pressure be larger than for the electronic gap. Indeed, based on our results for 1, we estimated that the exciton binding energy, _E_b, of water

will be decreased by about 60% in going from ambient pressure to ~30 GPa, and that of ice VII/VIII by 40% (The _E_b of water at ambient conditions is about 2.4 eV (ref. 30)). Our estimate is

based on the relation , where _m_* is the electronic effective mass, _m_e the electron mass and _a_0 the Bohr radius31, and we assumed a negligible variation of the electronic effective

mass under pressure, as indicated by our band structure calculations (not shown). Our results for band gaps are consistent with those reported by Hermann and Schwerdtfeger23 for ice VIII,

using many body perturbation theory. These authors used the G0W0 approximation and the Bethe-Salpeter equation23 to compute absorption spectra, with a model dielectric function to

approximate the screened Coulomb interaction. In their model, the electronic dielectric constant was an input parameter. Our results are also consistent with those of Boero _et al._32 who

reported an increase in the band gap of supercritical water at 653 K, for densities larger than 0.5 g cm−3, by using _ab initio_ MD and the BLYP functional. RELATION BETWEEN REFRACTIVE INDEX

AND BAND GAP Our calculations showed that both the refractive index and the electronic gap of water and ice increase under pressure, up to at least 30 GPa. They also showed that _n_ of ice

is larger than that of the liquid, in spite of the latter having a smaller electronic gap. Thus, the simple inverse correlation between _E_g and _n_ used to interpret experiments, and valid

for a wide range of substances20, does not hold for water and ice. We show in the following that two reasons are responsible for this apparent anomalous behaviour: an increase in the

electronic density with pressure and hence of the plasma frequency , where _ρ_e is the density of valence electrons and _e_ the elementary charge; a change in the localization property of

the valence band of the liquid and solid, as P is increased, which in turn is responsible for changes in the strength of interband transitions. Interestingly, while for ice the increase in

_ρ_e (and _ω_fp) counterbalances the increase in _E_g and hence [1(0)−1]/ρ_e_ decreases under pressure, the corresponding quantity for water shows an increase (see Fig. 3). Ice and water

behave as several oxides33 in exhibiting a positive derivative of the refractive index, with respect to _ρ_e. However, for both water and ice the quantity is not a constant, as it would be

if the Penn model correctly described the relation between the dielectric constant and electronic gap, but it monotonically increases with pressure, at all T considered here. We therefore

adopted a higher level of theory and derived the real part of the electronic dielectric constant in the random phase approximation: where c and v are the conduction and valence band indices,

respectively, and the integral is over the Brillouin Zone (BZ). In the integrand, is the oscillator strength in the polarization direction associated with the transition between the bands c

and v, and is the corresponding transition energy. In the case of water, only the Γ point was used in our electronic structure calculations; at zero frequency one has: where _V_ is the

volume of the simulation cell. Note that in a single-oscillator model with ℏ_ω_cv=_E_g, Equation 2 reduces to the Penn model, once the oscillator strength sum rule is applied. The oscillator

strength is given by where ‹c| and |› denote Kohn-Sham orbitals corresponding to valence (v) and conduction (c) states, and 2 is the imaginary part of the dielectric function. For v to c

transitions right across the band gap, the oscillator strength is proportional to [2(ωcv)_V_ωcv]. In Fig. 4 we plotted 2(_ω_)_V_ of two water configurations at 1,000 K, at ~1 GPa and ~10 

GPa. These are representative of a set of 25 and 55 snapshots analysed for each pressure, extracted from our MD trajectories at equally spaced simulation times; for each of them we found

that at ℏ_ω_=_E_g, 2_V_ is much larger at ~10 GPa than at ~1 GPa. The oscillator strength of the transitions just across the band gap, which yields the largest contribution to 1(0) according

to Equation 2, is thus substantially enhanced when the pressure increases from ~1 GPa to ~10 GPa, and the absorption edge is blue shifted, as expected from our electronic gap calculations.

We conclude that it is because of the enhancement of , which outweighs the increase of _E_g, that the refractive index of water increases under pressure. We note that local field effects are

not included in Equation 1 (ref. 34); they are instead taken into account in our density functional perturbation theory (DFPT)35 calculation of the refractive index (Denote the matrix

elements of the static dielectric matrix _GG_′(0), where _G_ and _G_′ are reciprocal lattice vectors; , implying that is the first element of the inverse dielectric matrix (ref. 35)).

However, in Equation 1, 1(0) is simply 00(0) and so called local field effects are neglected34). We verified that neglecting such effects amounts to a negligible error in the calculations of

_n_. In Fig. 5, we compare 1(0) of ice VIII, as well as that of high pressure water, obtained with and without local field corrections. The two sets of values are rigidly shifted by only

0.1~0.2 with respect to each other, indicating that none of the trends as a function of pressure reported here is affected by the inclusion of local field effects. LOCALIZATION PROPERTIES OF

WATER AND ICE VALENCE BAND EDGES To understand the changes in the oscillator strength of water under high pressure, we computed the inverse participation ratios (IPRs) of the VBM and CBM

orbitals; they are reported in Fig. 6. The IPR is defined as where _N_ is the total number of points used to perform integrals over a real space grid, and is the wave function associated

with the band α. The quantity _IPR_α yields the statistical variance for the distribution of . The larger the IPR, the more localized the wave function. An _IPR_α close to 1 indicates a

delocalized electronic orbital. Figure 6 shows that, under pressure, as at ambient conditions, the CBM of water is much more delocalized than its VBM37. The interesting finding is that with

increasing pressure the localization properties of the CBM are largely unaffected, while those of the VBM change substantially, with a tendency of the VBM to delocalize. The electronic

states of ice VIII behave similarly except that the variation of the VBM localization as a function of P is smaller than that of water, as shown in Fig. 6c. As a result, under pressure the

spatial overlap between the electron and hole wave functions is enhanced, and the matrix element increases (see Eq. 3). The fact that the localization of the CBM does not change

significantly under pressure, while that of the VBM substantially changes, suggests that the opening of the gap in ice and water under pressure might be mostly due to a change in the

position of the VBM. Experimentally Zha _et al._16 measured _n_ as a function of _ω_ and obtained two parameters, _E_d and _E__0_ from the equation _n_2−1 = _E__d__E_0/(_E_02−ℏ2ω2). The fit

was then used to conclude that the gap of ice decreases under pressure. Note that in the experiment of ref. 16 when the light wavelength is between 569 to 741 nm, _n_ changes by <0.05; as

a result, the effective band gap determined from the single-oscillator model changes little with pressure. It is presumably difficult to estimate _E_d and _E_0. The values for _E_d and _E_0

obtained from the fits gave a predicted closing of the band gap only at ultrahigh pressures (~4.5 TPa), well beyond the pressure range of the measurements. We have shown here that

state-of-the-art calculations of the electronic structure are essential to properly interpret complex and sophisticated optical experiments and obtain the correct band gap trend under

pressure. DISCUSSION We reported the first data for the refractive index of supercritical water above 7 GPa and at high temperature. We showed that the refractive index, and the electronic

and optical gaps of water and ice increase under pressure, and thus water properties differ substantially from those of apolar molecular fluids and solids, for example, hydrogen38,

methane39,40 and benzene41,42, whose electronic gaps decrease with pressure but refractive indices increase. We showed that the unusual relationship between _n_ and _E__g_ stems from an

enhancement of the strength of interband transitions right across the band gap. This enhancement, in combination with a decrease of the volume, outweighs the increase in the band gap upon

compression, and hence the refractive index of water increases with increasing pressure. The behaviour of the interband transition strength originates from the delocalization of the valence

band edge, whose overlap with the CBM increases with pressure. Our results showed that the use of simple models, for example, the Penn model17, to relate measured refractive indices to band

gaps of molecular fluids and crystals should be revisited and in general complex electronic structure effects should be taken into account, when predicting values of band gaps. We emphasize

that the type of electronic structure calculations reported here allows one to infer the band gap of water from high pressure measurements of the refractive index16. Measurements of the band

gap of water by light absorption or emission are not yet feasible under pressure, in diamond anvil cells; therefore, establishing the correlation between the band gap and the refractive

index is a crucial step to infer band gaps from measured dielectric constants. In general, _ab initio_ calculations play a key role in interpreting measurements of fluids under pressure,

especially in unraveling their electronic structure. Finally, we note that the results reported here for gaps and dielectric constants are expected to have an important impact in the broad

field of water-related science. For example, factors determining the rate of electron transfer in aqueous environments (and hence several chemical reactions occurring in these media) include

the refractive index and the static dielectric constant of the medium3. Hence, knowledge of such quantities is key to predict reorganization energies and electron transfer rates in

supercritical water and water under pressure, for example, in the Earth’s interior. In addition, the mobility of charges created in water by, e.g., photo-excitation, depends, among other

factors, on the exciton binding energy (_E_b); our results indicate that _E_b decreases under pressure and hence charge mobility is expected to change substantially in supercritical water,

with respect to water at ambient conditions, with implications for charge transport under bias, in supercritical conditions. METHODS WATER We carried out _ab initio_ MD simulations of water

under pressure as a function of temperature in the Born-Oppenheimer approximation with the Qbox code (version 1.54.2, http://eslab.ucdavis.edu/software/qbox/)43. We used 128-molecule unit

cells with periodic boundary conditions, plane-wave basis sets and norm conserving pseudopotentials (Gygi, F. Pseudopotential Table, http://fpmd.ucdavis.edu/potentials/index.htm). Atomic

trajectories were generated with a plane-wave kinetic energy cutoff of 85 Ry, which was then increased to 220 Ry for the calculation of pressure on selected snapshots26. ICE VIII

Calculations for ice VIII were conducted by using a 8-molecule unit cell with a plane-wave energy cutoff of 220 Ry and 4 × 4 × 3 k-point mesh and a 96-molecule supercell with a cutoff of 85 

Ry and Γ point only. ELECTRONIC STRUCTURE CALCULATIONS Trajectories were generated with the PBE exchange correlation functional24, while electronic gaps and dielectric constants were

computed with both the PBE and PBE0 (refs 27, 28) functionals on snapshots extracted from PBE trajectories. At the PBE level, the electronic dielectric constant 1 was calculated using

density functional perturbation theory (DFPT)36, as recently implemented in the Qbox code for the calculation of Raman spectra44. At the PBE0 level of theory, we instead used an electronic

enthalpy functional45, where the polarization was computed using maximally localized Wannier functions46 with a correction scheme47. We calculated the strengths of inter band transitions

with the Quantum-expresso package48. We used a Gaussian broadening parameter equal to 0.001 eV. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Pan D. _et al._ The refractive index and

electronic gap of water and ice increase with increasing pressure. _Nat. Commun._ 5:3919 doi: 10.1038/ncomms4919 (2014). REFERENCES * Weingärtner, H. & Franck, E. Supercritical water as

a solvent. _Angew. Chem. Int. Ed._ 44, 2672–2692 (2005). Article  Google Scholar  * Liebscher, A. Aqueous fluids at elevated pressure and temperature. _Geofluids_ 10, 3–19 (2010). Article 

CAS  Google Scholar  * Chandler, D. in _Computer Simulation of Rare Events and Dynamics of Classical and Quantum Condensed-Phase Systems–Classical and Quantum Dynamics in Condensed Phase

Simulations_ (eds Berne, B. J., Ciccotti, G., Coke, D. F.) 25–49 (World Scientific, 1998). * Marcus, R. A. On the theory of oxidation-reduction reactions involving electron transfer. I. _J.

Chem. Phys._ 24, 966–978 (1956). Article  CAS  ADS  Google Scholar  * Hama, J., Shiomi, Y. & Suito, K. Equation of state and metallization of ice under very high pressure. _J. Phys.

Condens. Matter_ 2, 8107 (1990). Article  CAS  ADS  Google Scholar  * Cavazzoni, C. et al. Superionic and metallic states of water and ammonia at giant planet conditions. _Science_ 283,

44–46 (1999). Article  CAS  ADS  Google Scholar  * Mattsson, T. R. & Desjarlais, M. P. Phase diagram and electrical conductivity of high energy-density water from density functional

theory. _Phys. Rev. Lett._ 97, 017801 (2006). Article  ADS  Google Scholar  * Hermann, A., Ashcroft, N. & Hoffmann, R. High pressure ices. _Proc. Natl Acad. Sci._ 109, 745–750 (2012).

Article  CAS  ADS  Google Scholar  * Clark, C. D., Dean, P. J. & Harris, P. V. Intrinsic edge absorption in diamond. _Proc. R Soc. London A_ 277, 312–329 (1964). Article  CAS  ADS 

Google Scholar  * Bernas, A., Ferradini, C. & Jay-Gerin, J.-P. On the electronic structure of liquid water: Facts and reflections. _Chem. Phys._ 222, 151–160 (1997). Article  CAS  Google

Scholar  * Pham, T. A., Zhang, C., Schwegler, E. & Galli, G. Probing the electronic structure of liquid water with many-body perturbation theory. _Phys. Rev. B_ 89, 060202 (2014).

Article  ADS  Google Scholar  * Kerr, G. D., Hamm, R. N., Williams, M. W., Birkhoff, R. D. & Painter, L. R. Optical and dielectric properties of water in the vacuum ultraviolet. _Phys.

Rev. A_ 5, 2523–2527 (1972). Article  ADS  Google Scholar  * Hermann, A., Schmidt, W. G. & Schwerdtfeger, P. Resolving the optical spectrum of water: coordination and electrostatic

effects. _Phys. Rev. Lett._ 100, 207403 (2008). Article  CAS  ADS  Google Scholar  * Pruzan, P. h., Chervin, J. C. & Canny, B. Stability domain of the ice VIII proton-ordered phase at

very high pressure and low temperature. _J. Chem. Phys._ 99, 9842 (1993). Article  CAS  ADS  Google Scholar  * Murray, E. D. & Galli, G. Dispersion interactions and vibrational effects

in ice as a function of pressure: a first principles study. _Phys. Rev. Lett._ 108, 105502 (2012). Article  ADS  Google Scholar  * Zha, C.-S., Hemley, R. J., Gramsch, S. A., Mao, H.-k. &

Bassett, W. A. Optical study of H2O ice to 120 GPa: Dielectric function, molecular polarizability, and equation of state. _J. Chem. Phys._ 126, 074506 (2007). Article  ADS  Google Scholar 

* Penn, D. R. Wave-number-dependent dielectric function of semiconductors. _Phys. Rev._ 128, 2093–2097 (1962). Article  CAS  ADS  Google Scholar  * Hemley, R. J., Hanfland, M. & Mao, H.

K. High-pressure dielectric measurements of solid hydrogen to 170 GPa. _Nature_ 350, 488 (1991). Article  CAS  ADS  Google Scholar  * Loubeyre, P., Occelli, F. & LeToullec, R. Optical

studies of solid hydrogen to 320 GPa and evidence for black hydrogen. _Nature_ 416, 613–617 (2002). Article  CAS  ADS  Google Scholar  * Wemple, S. H. & DiDomenico, M. Jr Behavior of the

electronic dielectric constant in covalent and ionic materials. _Phys. Rev. B_ 3, 1338 (1971). Article  ADS  Google Scholar  * Kittel, C. _Introduction to Solid State Physics_ 8th edn John

Wiley & Sons (2005). * Sanchez-Valle, C., Mantegazzi, D., Bass, J. D. & Reusser, E. Equation of state, refractive index and polarizability of compressed water to 7 GPa and 673 K. _J.

Chem. Phys._ 138, 054505 (2013). Article  ADS  Google Scholar  * Hermann, A. & Schwerdtfeger, P. Blueshifting the onset of optical UV absorption for water under pressure. _Phys. Rev.

Lett._ 106, 187403 (2011). Article  ADS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996).

Article  CAS  ADS  Google Scholar  * Galli, G. & Pan, D. A closer look at supercritical water. _Proc. Natl Acad. Sci. USA_ 110, 6250–6251 (2013). Article  CAS  ADS  Google Scholar  *

Pan, D., Spanu, L., Harrison, B., Sverjensky, D. A. & Galli, G. Dielectric properties of water under extreme conditions and transport of carbonates in the deep earth. _Proc. Natl Acad.

Sci. USA_ 110, 6646–6650 (2013). Article  CAS  ADS  Google Scholar  * Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. _J.

Chem. Phys._ 110, 6158 (1999). Article  CAS  ADS  Google Scholar  * Gygi, F. & Duchemin, I. Efficient computation of Hartree-Fock exchange using recursive subspace bisection. _J. Chem.

Theory Comput._ 9, 582–587 (2012). Article  Google Scholar  * Schönherr, M., Slater, B., Hutter, J. & VandeVondele, J. Dielectric properties of water ice, the ice Ih/XI phase transition

and an assessment of DFT. _J. Phys. Chem. B_ 118, 590–596 (2014). Article  Google Scholar  * Garbuio, V., Cascella, M., Reining, L., Sole, R. D. & Pulci, O. Ab initio calculation of

optical spectra of liquids: many-body effects in the electronic excitations of water. _Phys. Rev. Lett._ 97, 137402 (2006). Article  CAS  ADS  Google Scholar  * Dvorak, M., Wei, S.-H. &

Wu, Z. Origin of the variation of exciton binding energy in semiconductors. _Phys. Rev. Lett._ 110, 016402 (2013). Article  ADS  Google Scholar  * Boero, M., Terakura, K., Ikeshoji, T.,

Liew, C. C. & Parrinello, M. Water at supercritical conditions: A first principles study. _J. Chem. Phys._ 115, 2219 (2001). Article  CAS  ADS  Google Scholar  * Waxler, R. M. &

Cleek, G. W. The effect of temperature and pressure on the refractive index of some oxide glasses. _J. Res. Natl Bur. Stand. Sect. A_ 77, 755–763 (1973). Article  CAS  Google Scholar  *

Wiser, N. Dielectric constant with local field effects included. _Phys. Rev._ 129, 62–69 (1963). Article  ADS  Google Scholar  * Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi,

P. Phonons and related crystal properties from density-functional perturbation theory. _Rev. Mod. Phys._ 73, 515–562 (2001). Article  CAS  ADS  Google Scholar  * Ping, Y., Rocca, D. &

Galli, G. Electronic excitations in light absorbers for photoelectrochemical energy conversion: first principles calculations based on many body perturbation theory. _Chem. Soc. Rev._ 42,

2437–2469 (2013). Article  CAS  Google Scholar  * Laasonen, K., Sprik, M., Parrinello, M. & Car, R. ‘Ab initio’ liquid water. _J. Chem. Phys._ 99, 9080 (1993). Article  CAS  ADS  Google

Scholar  * García, A. et al. Dielectric properties of solid molecular hydrogen at high pressure. _Phys. Rev. B_ 45, 9709–9715 (1992). Article  ADS  Google Scholar  * Lin, H., Li, Y.-l.,

Zeng, Z., Chen, X.-j. & Lin, H. Structural, electronic, and dynamical properties of methane under high pressure. _J. Chem. Phys._ 134, 064515 (2011). Article  ADS  Google Scholar  *

Hebert, P., Polian, A., Loubeyre, P. & Le Toullec, R. Optical studies of methane under high pressure. _Phys. Rev. B_ 36, 9196–9201 (1987). Article  CAS  ADS  Google Scholar  * Wen,

X.-D., Hoffmann, R. & Ashcroft, N. Benzene under high pressure: a story of molecular crystals transforming to saturated networks, with a possible intermediate metallic phase. _J. Am.

Chem. Soc._ 133, 9023–9035 (2011). Article  CAS  Google Scholar  * Takagi, T. & Teranishi, H. Refractive index of liquids under high pressure. _J. Chem. Eng. Data_ 27, 16–18 (1982).

Article  CAS  Google Scholar  * Gygi, F. Architecture of qbox: A scalable first-principles molecular dynamics code. _IBM J. Res. Dev_ 52, 137–144 (2008). Article  Google Scholar  * Wan, Q.,

Spanu, L., Galli, G. A. & Gygi, F. Raman spectra of liquid water from ab initio molecular dynamics: vibrational signatures of charge fluctuations in the hydrogen bond network. _J. Chem.

Theory Comput._ 9, 4124–4130 (2013). Article  CAS  Google Scholar  * Souza, I., Íñiguez, J. & Vanderbilt, D. First-principles approach to insulators in finite electric fields. _Phys.

Rev. Lett._ 89, 117602 (2002). Article  ADS  Google Scholar  * Marzari, N., Mostofi, A., Yates, J., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: Theory and

applications. _Rev. Mod. Phys._ 84, 1419–1475 (2012). Article  CAS  ADS  Google Scholar  * Stengel, M. & Spaldin, N. Accurate polarization within a unified Wannier function formalism.

_Phys. Rev. B_ 73, 075121 (2006). Article  ADS  Google Scholar  * Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. _J

Phys. Condens. Matter_ 21, 395502 (2009). Article  Google Scholar  Download references ACKNOWLEDGEMENTS We thank F. Gygi, M. Govoni and Y. Ping for many useful discussions and R. Hemley for

a critical reading of the manuscript. This work was supported by Department of Energy (DOE), Computer Materials and Chemical Sciences Network, under Grant DE-SC0005180, and by the Sloan

Foundation through the Deep Carbon Observatory. Part of this work was carried out using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE),

provided by the National Institute for Computational Sciences (NICS) under Grant TG-MCA06N063, which is funded by the National Science Foundation; and resources at Lawrence Berkeley National

Laboratory, NERSC, supported by DOE under Contract No. DE-FG02-06ER46262. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Chemistry, University of California, Davis, 95616,

California, USA Ding Pan & Quan Wan * The Institute for Molecular Engineering, University of Chicago, Chicago, 60637, Illinois, USA Quan Wan & Giulia Galli Authors * Ding Pan View

author publications You can also search for this author inPubMed Google Scholar * Quan Wan View author publications You can also search for this author inPubMed Google Scholar * Giulia Galli

View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.P. and G.G. designed the research. Most of the calculations were performed by D.P., with

contributions from all authors. Q.W. implemented a Density Functional Perturbation Theory (used for the calculation of the dielectric constants) into the Qbox code. All authors contributed

to the analysis and discussion of the data and the writing of the manuscript. CORRESPONDING AUTHOR Correspondence to Ding Pan. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no

competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images or other third

party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative

Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit

http://creativecommons.org/licenses/by-nc-sa/3.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Pan, D., Wan, Q. & Galli, G. The refractive index and electronic gap of

water and ice increase with increasing pressure. _Nat Commun_ 5, 3919 (2014). https://doi.org/10.1038/ncomms4919 Download citation * Received: 21 January 2014 * Accepted: 16 April 2014 *

Published: 27 May 2014 * DOI: https://doi.org/10.1038/ncomms4919 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative