Hippocampus segmentation based on local linear mapping

ABSTRACT We propose local linear mapping (LLM), a novel fusion framework for distance field (DF) to perform automatic hippocampus segmentation. A k-means cluster method is propose for

constructing magnetic resonance (MR) and DF dictionaries. In LLM, we assume that the MR and DF samples are located on two nonlinear manifolds and the mapping from the MR manifold to the DF

manifold is differentiable and locally linear. We combine the MR dictionary using local linear representation to present the test sample, and combine the DF dictionary using the

corresponding coefficients derived from local linear representation procedure to predict the DF of the test sample. We then merge the overlapped predicted DF patch to obtain the DF value of

each point in the test image via a confidence-based weighted average method. This approach enabled us to estimate the label of the test image according to the predicted DF. The proposed

method was evaluated on brain images of 35 subjects obtained from SATA dataset. Results indicate the effectiveness of the proposed method, which yields mean Dice similarity coefficients of

0.8697, 0.8770 and 0.8734 for the left, right and bi-lateral hippocampus, respectively. SIMILAR CONTENT BEING VIEWED BY OTHERS A PAIRED DATASET OF MULTI-MODAL MRI AT 3 TESLA AND 7 TESLA WITH

MANUAL HIPPOCAMPAL SUBFIELD SEGMENTATIONS Article Open access 13 February 2025 RADIUS-OPTIMIZED EFFICIENT TEMPLATE MATCHING FOR LESION DETECTION FROM BRAIN IMAGES Article Open access 02

June 2021 DSNET: A NEW DUAL-BRANCH NETWORK FOR HIPPOCAMPUS SUBFIELD SEGMENTATION Article Open access 03 July 2024 INTRODUCTION The accurate and reliable segmentation of deep brain

structures, such as the hippocampus, in magnetic resonance (MR) images has gained considerable scientific attention because of the widespread use of MRI. The segmentation of deep brain

structures is a key requirement for the assessment, treatment, and follow-up of various mental disorders1,2. The hippocampus is located in the medial temporal lobe, which is the site of

structural and functional pathologies in mental illnesses. Changes in the size and shape of the hippocampus are closely related to Alzheimer’s and other diseases. Morphological analysis and

shape comparisons of the hippocampus from healthy and diseased subjects can identify abnormal deformations; such findings can facilitate possible biomarker identification, prognosis and

diagnosis of diseases, and optimum treatment identification3,4,5. Hippocampus segmentation should be conducted for these applications. The manual segmentation of the hippocampus from MR

images is tedious, time-consuming, susceptible to human errors, nonreproducible, and expensive. Automatic segmentation offers reasonable promises, but remains challenging because of noise,

limited resolution, and partial volume effect, resulting in weak boundaries of the hippocampus in MR images4,6. At present, the segmentation accuracy of the hippocampus remains relatively

low7,8,9,10. Atlas-based segmentation is a powerful and popular technique for automatic delineation of structures in volumetric images9,11,12,13,14,15,16,17,18, especially the

hippocampus18,19,20. Atlas-based methods are initiated by registering an atlas with the target image to be segmented. The manual label of the atlas associated with the training images is

thus propagated to the target image by using the mapping determined during the registration. The quality of atlas-based segmentation is affected by the bias and the accuracy of registration,

as well as the label fusion method. Multiple atlases can be separately registered to the target image to avoid biased registration7,10,19,20,21,22,23,24,25. The corresponding label of each

atlas is warped to the target image space through the deformation field derived from the registration procedure. Combining the warped labels from all atlases generates a fused label as the

segmentation of the target image. Several studies demonstrated that multi-atlas segmentation methods significantly outperform schemes that use a single atlas7,10,19,20,21,22,23,24.

Patch-based label fusion methods have been proposed to alleviate the dependence of the accurate registration21,26. In these methods, the atlases only need to be aligned to the target image

space through linear registration. The labels of each patch of the target image are calculated by fusing the labels of similar patches located in the surrounding region in the aligned

atlases. The patch-based method has demonstrated promising segmentation results without need for accurate non-rigid registrations. Another approach to further improve the quality of

multi-atlas based segmentation is to develop more accurate and robust label fusion methods. The most straightforward label fusion method is the majority vote on a per-voxel basis18. A recent

work demonstrated that weighted averaging can be used to improve the quality of segmentation19. This approach suggests that an atlas which bears similarities with the target image should

carry more weight during label fusion. Most existing label fusion methods are based on weighted voting, in which each atlas contributes to the final solution according to a nonnegative

weight; in this method, atlases that bear similarities with the target image receive larger weights10. Among weighted voting methods, those that derive weights from local similarity between

the atlas and target, and thus allow the weights to vary spatially, have been the most successful in practice. Another popular approach is called simultaneous truth and performance level

estimation (STAPLE), which uses an expectation-maximization (EM) approach to obtain the best possible final segmentation27. Spatial STAPLE is an extension of the traditional STAPLE framework

that enables the estimation of a smooth spatially varying performance level field instead of global performance level parameters and has been shown to provide robust and accurate

multi-atlas segmentations20. For the patch-based label fusion method, the weights of the fused labels are calculated using a non-local means approach28 or local linear representation-based

method26. This study is an expansion of the preliminary research29, which demonstrated that the use of distance field (DF) improved the accuracy of hippocampus segmentation. In ref. 29, the

image patches and DF patches were assumed to be located on different nonlinear manifolds, and the mapping between these manifolds approximated a diffeomorphism under a local constraint.

Based on the two assumptions, a distance field fusion (DFF) method was proposed to perform hippocampus segmentation. This method produced promising segmentation results, but two drawbacks

were identified in ref. 29. First, training subjects need to be non-rigidly registered to each test subject, which require large memory and complicated computation. Second, high computation

costs were required in constructing a dictionary because different test samples use distinct dictionaries. In this paper, we propose a method based on local linear mapping (LLM) to segment

the hippocampus from the MR brain image. The present study achieved the following improvements compared with the preliminary version29. First, we use a fixed dictionary instead of an

adaptive dictionary to estimate the DF of the target object (hippocampus in this study). Non-rigid registration is not required for the test image thereby reducing computation and memory

costs. The MR image patches and DF patches are assumed to be located on different nonlinear manifolds, and the mapping between these two manifolds is differentiable and linear under a local

constraint. The fusion weights of the DF patches can be deduced from the weights of MR image patches. Based on these assumptions, a compact dictionary is constructed via the k-means cluster

method. The DFs of test samples are predicted using LLM. Second, a novel confidence-based weighted average (CWA) method is proposed to merge the overlapped DF patch prediction for each test

sample. In CWA, the weight used to predict the DF value of a point is dependent on a residual of local linear representation, wherein large residual indicates less weight and vice versa. The

proposed method is evaluated on 35 subjects, which include 20 training subjects, 5 optimization subjects and 10 test subjects. Results show that the proposed method can generate a more

promising hippocampus segmentation than that in existing methods18,20,27,30,31. The rest of this paper is organized as follows. In Section “Datasets”, we describe the datasets. In Section

“Methods”, we show the details of the proposed LLM. In Section “Experimental results”, we present the experiments and results. In Section “Discussion”, discussion is provided. DATASETS Our

dataset is obtained from SATA Segmentation Challenge Dataset (https://my.vanderbilt.edu/masi/workshops/). We use the subdataset in the dataset to perform the experiments. The subdataset

consists of 35 subjects. Each subject includes a T1-weighted MR brain image and a manually delineated label image. The size of the voxels of the images is 1 × 1 × 1 mm3. Each image consists

of several slices with the resolution of 256 × 256 (pixels) and the numbers of slices range from 261 to 334. We randomly select 20 subjects as training dataset, 5 as optimization dataset and

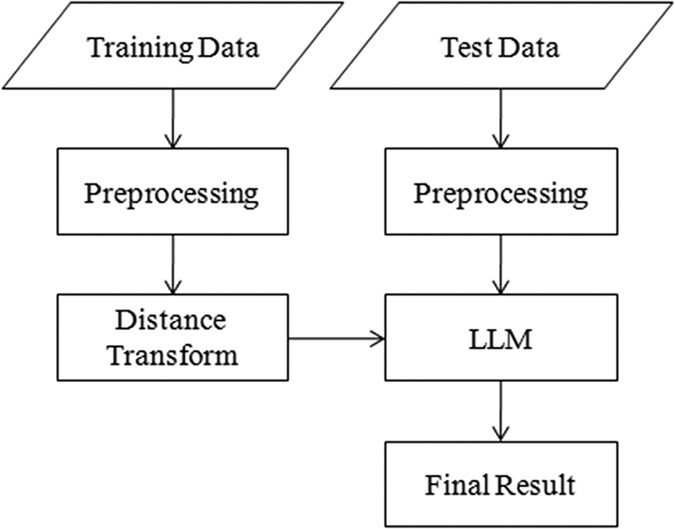
10 as test dataset. METHODS The proposed method contains three parts, namely, preprocessing, distance transform, and LLM-based segmentation. The framework of the proposed method is shown in

Fig. 1. LLM BASIC IDEA OF LLM Given a set of MR images and corresponding DF images associated with the hippocampus, we aim to predict the DF for the test image. The segmentation problem is

described as follows. Given a training dataset which consists of _N_ MR/DF image patch pairs, we want to calculate the patch of a test MR image patch . We construct a compact dictionary

through to reduce computation and memory costs caused by the tremendous size of . and denote the MR dictionary and the DF dictionary, respectively. The dimension of atom vector equates to

that of . The proposed LLM is based on two assumptions. _ASSUMPTION I:_ _ Image patches from MR image and DF are located on different nonlinear manifolds, and a patch can be approximately

represented as a linear combination of several nearest neighbors from its manifolds._ _ASSUMPTION II:_ _ Under a local constraint, the mapping from MR manifold to DF manifold_ _is

differentiable and linear._ Assumption I was verified in many studies26,32,33. In the present study, manifolds and , which respectively denote the manifolds of MR and DF, are assumed to be

spanned by patches in dictionary . Test image patch can be linearly represented as follows: where _ε_ is the reconstruction error of sample and _τ_ is a small non-negative constant. is a set

that consists of the _k_-nearest neighbors of sample in dictionary . Based on Assumption II, a local region on manifold _M__MR_ can be mapped to a local region on manifold _M__DF_, and the

mapping _f_ between these two local regions is linear. The DF of the test patch can be calculated as Equation (2) shows that the weight in the original MR image patch space can be

transformed to the DF patch space under Assumption I and II. The locality of the sample space is crucial for the rationality of Assumption II. The locality in the sample space means only in

the local regions on manifolds _M__MR_ and _M__DF_, _f_ is linear and Eq. (2) can be deduced. To maintain the locality of the sample space, we need to gather sufficient samples. Thus for

each test sample, dense samples span its local region. The drawback of this approach is the need for a large training dataset. Such a requirement leads to high computation and memory costs.

In addition, an appropriate local linear representation method should be selected to solve Eq. (1) in a local region (detailed in Section “Local linear representation”). In this paper, a

dictionary construction method based on k-means cluster is proposed to reduce computation and memory costs. DICTIONARY CONSTRUCTION A dictionary can be constructed using original training

dataset _T_. However, numerous training samples possibly produce a large dictionary which contains redundant information and requires large memory and computation costs. Previous

studies26,34 indicated that the k-means cluster method produces a representative dictionary for local linear representation. To reduce computation and memory costs, we use the k-means method

to cluster the MR training samples and the cluster centers are selected as the atom vectors of MR dictionary _D__MR_. The atom vector of _D__MR_ is denoted as: where _G__i_ is a sub-set,

and each is closest to in _D__MR_, i.e. is the cluster center of _G__i_, and is the size of _G__i_. In Eq. (3), is the neighbor of . Based on Assumption II, mapping _f_ from manifold _M__MR_

to _M__DF_ is locally linear. Therefore, the atom vector of DF dictionary _D__DF_ is denoted as: where is the DT patch that corresponds to . LOCAL LINEAR REPRESENTATION Several methods have

been proposed to represent a test sample linearly by combining training samples. Sparse coding with L1 LASSO35 emphasizes the sparsity of coefficients. This approach represents a test

sample with the least training samples and minimal construction error. Locality-constrained linear coding (LLC)36 emphasizes the locality rather than sparsity. This method represents a test

sample using several training samples located in a local region around the test sample. Compared with LLC, local anchor embedding (LAE)37 adds a non-negative constraint to the coefficients

to ensure that the test sample is represented by the convex combination of its closest neighbors and further enhances locality. LLC is selected in local linear representation because it

outperforms LAE. According to our context, the cost function of LLC is defined as follows: where is a set which is composed of the _k_-nearest neighbors of the test sample in , and is the

coefficient vector of _D__MR_. DF PREDICTION AND HIPPOCAMPUS SEGMENTATION VIA CWA The corresponding patch of test patch can be predicted using Eq. (2). We slide the patch across the test

image step by step, ensuring that patches overlap. For a point _p_ in the test image, we can obtain a series of predicted DF values from the overlapped patches. In ref. 29, the average of

these predicted values was used as the final estimator for point _p_. The overlapped patches around the point _p_ equally contributed to the DF prediction of _p_. However, the confidences of

DF prediction from different patches around _p_ are different, which result in various contributions for DF prediction. To address this issue, we propose a novel CWA strategy to predict the

DF value of _p_. The weighted average of DF values predicted from overlapped patches around _p_ is utilized as the final estimator for _p_, and the weights for overlapped patches are

calculated by the confidence of DF prediction. We evaluate the confidence by the residual of local linear representation, i.e., larger residual indicates less confidence and vice versa.

Based on this analysis, the weight of the point _u_ in the patch centered at point _p_ is calculated as follows: where _w__u_ is the coefficient vector calculated via Eq. (5); denotes the

patch centered at point ; is the L2 norm that indicates the residual of local linear representation; _σ_ is a decay parameter. When _σ_ is small, only a few more confident patches contribute

to DF prediction for _p_. When _σ_ is large, all patches around _p_ tend to have similar weights and the prediction is similar to a classical average. The value of _σ_ should depend on the

residuals of the local linear representation of patches centered at points around _p_. When the reconstruction residual of a patch center at a point around _p_ is extremely small, _σ_ should

be decreased to reduce the influence of other patches. By contrast, when the reconstruction residuals of patches centered at points around _p_ are extremely large, _σ_ should be increased

to relax the selection. To achieve the automatic selection of _σ_, we introduce the local adaptation of _σ_21 as follows: We then obtain the DF value for point _p_ using the following

formula: where denotes the DF value of _p_ estimated by patch using Eq. (2). The label of point _p_ can be calculated as PREPROCESSING The intensity of MR images is normalized to remove

variation in image intensity caused by different coordinate systems, head positions, non-uniformity of image intensity, and other artifacts. The BET approach38 is applied to remove the skull

in MR images; the N4 algorithm39 is utilized to remove the bias field artifacts from MR images. All training MR images were non-rigidly registered to a randomly selected MR image via

DRAMMS40; the average of wrapped MR images and label images are used as average template and average label template, respectively. For each test MR image, the average template was linearly

registered to the test MR image via FLIRT41 using default parameters. The wrapped average label template is utilized to extract ROI around the hippocampus; as such, computational burden is

reduced. Training and test samples are extracted in the original image space. DISTANCE TRANSFORM The absolute value of DF at a point _p_ denotes the distance between _p_ and the closest

point from the boundary of the target (i.e. hippocampus). The sign denotes whether the point _p_ belongs to the hippocampus. A positive sign indicates that _p_ is inside the boundary of the

hippocampus and vice versa. Figure 2 shows an example of the DF of a hippocampus image. The DF patch provides the label information and the distance information from the boundary. We used

the method proposed by Maurer42 to calculate the DF of a label image. SUMMARY OF THE PROPOSED METHOD We provide a pseudo-code in Algorithm 1 to illustrate the proposed method. EXPERIMENTAL

RESULTS We applied the proposed method to 35 subjects. A total of 20 subjects comprised the training dataset, 5 subjects comprised the optimization dataset, and 10 subjects were test

dataset. The training dataset was used to construct the dictionary, and the optimization dataset was utilized to optimize parameters, which were used to perform the subsequent experiments

using the test dataset to evaluate the performance of the proposed method. The number of nearest neighbors in LLC and LAE was 30, and the step of sliding the patch was  mm3 in all

experiments. To evaluate the performance of the methods, we used Dice similarity coefficient (DSC) as the quantitative metric34, which is defined as: where _A_ and _B_ denote the voxel sets

of the segmentation result and ground truth, respectively. DSC was used to measure the similarity between the ground truth and the automatic segmentation results. A set of experiments were

presented to evaluate the performance of the proposed method. These experiments include (1) parameter choices, (2) contribution of CWA, (3) comparison with state-of-the-art methods. A PC

with Intel Xeon E5-2620 2.0 GHz processor and 96GB RAM was used as workstation. Our algorithm was implemented in MATLAB 2012b using single thread. Dictionary construction in the training

step lasted for 5 h. This dictionary contained 70,000 atoms and was extracted from a training dataset composed of 20 subjects. In the test step, the processing time was approximately 10 min,

including 6 min in preprocessing and 4 min in segmentation. PARAMETER CHOICES SELECTION OF THE NUMBER OF TRAINING SUBJECTS Figure 3 illustrates some of the parameter selection experiments,

in which the numbers of training subjects varied from 5 to 20 with an interval of 5. In these experiments, the sizes of patch and dictionary were fixed to and 50,000, respectively, and LLC

was used in local linear representation. Results show that a larger number of training subjects produce better results. We attribute this performance to the fact that a larger number of

training subjects generate more representative dictionary. Thus, 20 training subjects were selected to be the training dataset in the subsequent experiments. PARAMETER SETTING FOR THE SIZE

OF PATCH AND DICTIONARY Figure 4 shows the mean DSC for the segmentation of the left, right, and bi-lateral hippocampus over different sizes of patch and dictionary using LLC and LAE in

local linear representation. Patch sizes (Unit: mm3) ranged from to with an interval of . Dictionary sizes varied from 10,000 to 100,000 with an interval of 10,000. As shown in Fig. 4, DSC

increases significantly from patch size to the , which results from the fact that similar small MR patches could correspond to distinct DF patches and Assumption II is violated. Too large

size of patch could result in large distance between the patches in , thus Assumption I is difficult to ensure and the DSC of bi-lateral hippocampus segmentation decreases with the patch

size increasing from to . The result showed that a patch size of was a good choice for LLC and LAE. The accuracy of LLC was improved by increasing the size of dictionary. However,

improvement plateaued when the size of dictionary exceeded 70,000. Large dictionary size indicated high memory and computation costs. The sizes of the dictionary and patch for LLC were set

to 70,000 and , respectively. In LAE, with the dictionary size increasing, the accuracy of the left hippocampus declined and improvement of accuracy for the right hippocampus plateaued when

the size of dictionary exceeded 50,000. Therefore, the optimal sizes of dictionary and patch for LAE are 50,000 and , respectively. METHOD SELECTION IN LOCAL LINEAR REPRESENTATION Given that

LLC and LAE emphasize the locality in local linear representation, we performed the experiments using these methods to select an optimal method. Table 1 shows the mean DSC and standard

deviation of left, right, and bi-lateral hippocampus segmentation using LLC and LAE. As shown in Table 1, LLC significantly improved the accuracy compared with LAE, in which the average DSC

increased by 0.61%, 0.60% and 0.60% for left, right, and bi-lateral hippocampus, respectively. Therefore, LLC was selected for local linear representation in subsequent experiments.

CONTRIBUTION OF CWA Two groups of experiments were performed to verify the effectiveness of CWA. In the first group (denoted as With CWA), we performed the experiment using the proposed

method called LLM with CWA. In the other group (denoted as Without CWA), for a point in the test image, we obtained a series of predicted DF values via Eq. (2) from the overlapped patch and

the average of these predicted values was used as the final estimator for point . Figure 5 lists the DSC of 10 test subjects. Figure 5 shows that the method with CWA outperformed the method

without CWA for most of subjects. Table 2 demonstrates the mean DSC and standard deviation of left, right, and bi-lateral hippocampus for 10 test subjects using methods with CWA and without

CWA. Compared to method without CWA, the mean DSC of left, right, and bi-lateral hippocampus of method with CWA increased significantly (paired t-test _p_ = 0.08, 0.049 and 0.009,

respectively) by 0.37%, 0.18% and 0.28%, respectively. COMPARISON WITH RELEVANT METHODS To investigate the contribution of LLM, we compared the proposed method with several state-of-the-art

label fusion algorithms and distance field fusion method, namely, majority voting18, SIMPLE31, STAPLE27, spatial STAPLE20, and DFF29. Label fusion algorithms (majority voting, SIMPLE,

STAPLE, and spatial STAPLE) were performed using MASI Label Fusion toolbox (http://www.nitrc.org/projects/masi-fusion) with default parameters. Table 3 shows the mean ± standard deviation of

DSC for the left, right, and bi-lateral hippocampus using different segmentation methods. The mean ± standard deviation of DSC obtained by the proposed method was 0.8697 ± 0.0091 for the

left hippocampus, 0.8770 ± 0.0176 for the right hippocampus, and 0.8734 ± 0.0113 for the bi-lateral hippocampus. Results showed that the proposed method generated higher accuracy than those

of the four relevant label fusion algorithms. Compared to DFF, the segmentation accuracy of LLM decreased by 0.31%, 0.55% and 0.43% for left, right, and bi-lateral hippocampus, respectively.

However, DFF is a multi-atlas based method that requires deformable registration. Given the trade-off between memory and computation costs and accuracy, the performance of the proposed

method LLM was comparable to that of DFF. Figure 6 shows the coronal view of segmentation results for the right hippocampus of a test subject using our method and five other methods. The

hippocampus segmented by our method was more similar to the ground-truth than in any other methods (i.e., majority voting, SIMPLE, STAPLE, spatial STAPLE and DFF). Particularly, in the arrow

region, our method could accurately delineate the boundary of the hippocampus, whereas the five other methods led to large errors. DISCUSSION In this study, we propose a novel LLM-based

method to segment hippocampus for MR image. The main contributions of this study are as follows. First, we utilize label information and distance information from the boundary of the

hippocampus to improve the segmentation accuracy of LLM. Second, we assume that MR image patches and DF patches are located on nonlinear manifolds, and the mapping between these manifolds is

locally linear and differentiable. The fusion weights of DF patches can be deduced from the weights of MR image patches. Third, according to Assumption II, a novel k-means based method is

proposed to build a compact dictionary that ensures the accuracy with limited computation and memory costs. Fourth, CWA is proposed to facilitate fusion of the overlapped prediction of DF.

Segmentation accuracy is significantly improved by the residual of local linear representation. In our previous study43, the dictionary was constructed by considering the locality of image

space (i.e. constructing the dictionary using the training samples around the test point in image space) and LAE was superior to LLC. However, in the current study, we neglected the locality

of image space and LLC outperformed LAE. We cannot provide a complete explanation for this phenomenon, but we assume that it is caused by the introduction of locality of image space in the

training dataset. In the current study, we conduct the experiments for T1-weighted MR brain image. In clinical setting, multi-modality image analysis is imperative for accurate diagnosis.

Conducting a comparison with different modalities may provide a better understanding of the effectiveness of the proposed method in clinical setting. In our future study, we will collect

more datasets of multiple modalities to expand the proposed method to multi-modality image analysis. Computation time can be improved. We use a single thread to perform our experiments. In

our method, we predict DF patches point-by-point. The procedure for predicting DF patches at different points is independent, which provides the possibility for parallel computation. In

future studies, parallel computation by multi-thread and GPU computation will be used to improve the speed of segmentation. Information on patch similarity and the feature distinctness

should be incorporated to enhance segmentation performance44,45. Moreover, as mentioned in Section “Introduction”, changes in the size and shape of hippocampus are closely related to

Alzheimer’s and other mention disorders, we will calculate the volume of hippocampus using the proposed method and study the relation between the size of hippocampus and Alzheimer’s in our

future work. In conclusion, this study presents a novel method for hippocampus segmentation based on LLM. The proposed method is compared with majority voting, SIMPLE, STAPLE, spatial

STAPLE, and DFF in public datasets. The accuracy of the proposed method is higher than the first four aforementioned label fusion methods and comparable with DFF. ADDITIONAL INFORMATION HOW

TO CITE THIS ARTICLE: Pang, S. _et al_. Hippocampus Segmentation Based on Local Linear Mapping. _Sci. Rep._ 7, 45501; doi: 10.1038/srep45501 (2017). PUBLISHER'S NOTE: Springer Nature

remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES * Dinggang, S. & Christos, D. Measuring temporal morphological changes

robustly in brain MR images via 4-dimensional template warping. _Neuroimage_ 21, 1508–1517 (2004). Article  Google Scholar  * Shattuck, D. W., Sandor-Leahy, S. R., Schaper, K. A.,

Rottenberg, D. A. & Leahy, R. M. Magnetic Resonance Image Tissue Classification Using a Partial Volume Model. _Neuroimage_ 13, 856–876 (2001). Article  CAS  PubMed  Google Scholar  *

Mueller, S. G. et al. The Alzheimer’s disease neuroimaging initiative. _Neuroimaging Clin N Am_ 15, 869–877, xi-xii, doi: 10.1016/j.nic.2005.09.008 (2005). Article  PubMed  PubMed Central 

Google Scholar  * Mueller, S. G. et al. Ways toward an early diagnosis in Alzheimer’s disease: the Alzheimer’s Disease Neuroimaging Initiative (ADNI). _Alzheimers Dement_ 1, 55–66, doi:

10.1016/j.jalz.2005.06.003 (2005). Article  PubMed  PubMed Central  Google Scholar  * Baillard, C., Hellier, P. & Barillot, C. Segmentation of brain 3D MR images using level sets and

dense registration. _Medical Image Analysis_ 5, 185–194 (2001). Article  CAS  PubMed  Google Scholar  * Barra, V. & Boire, J. Y. Automatic segmentation of subcortical brain structures in

MR images using information fusion. _IEEE Trans Med Imaging_ 20, 549–558, doi: 10.1109/42.932740 (2001). Article  CAS  PubMed  Google Scholar  * Hao, Y. et al. Local label learning (LLL)

for subcortical structure segmentation: application to hippocampus segmentation. _Hum Brain Mapp_ 35, 2674–2697, doi: 10.1002/hbm.22359 (2014). Article  PubMed  Google Scholar  * Tong, T.,

Wolz, R., Coupé, P., Hajnal, J. V. & Rueckert, D. Segmentation of MR images via discriminative dictionary learning and sparse coding: Application to hippocampus labeling. _Neuroimage_

76, 11–23 (2013). Article  PubMed  Google Scholar  * Kwak, K. et al. Fully-automated approach to hippocampus segmentation using a graph-cuts algorithm combined with atlas-based segmentation

and morphological opening. _Magn Reson Imaging_ 31, 1190–1196, doi: 10.1016/j.mri.2013.04.008 (2013). Article  PubMed  Google Scholar  * Kim, M. et al. Automatic hippocampus segmentation of

7.0 Tesla MR images by combining multiple atlases and auto-context models. _Neuroimage_ 83, 335–345 (2013). Article  PubMed  Google Scholar  * Carmichael, O. T. et al. Atlas-based

hippocampus segmentation in Alzheimer’s disease and mild cognitive impairment. _Neuroimage_ 27, 979–990, doi: http://dx.doi.org/10.1016/j.neuroimage.2005.05.005 (2005). Article  PubMed 

Google Scholar  * van der Lijn, F., den Heijer, T., Breteler, M. M. & Niessen, W. J. Hippocampus segmentation in MR images using atlas registration, voxel classification, and graph cuts.

_Neuroimage_ 43, 708–720, doi: 10.1016/j.neuroimage.2008.07.058 (2008). Article  PubMed  Google Scholar  * Rohlfing, T., Brandt, R., Menzel, R. & Maurer, C. R. Evaluation of atlas

selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. _Neuroimage_ 21, 1428–1442 (2004). Article  PubMed  Google Scholar  *

Gorthi, S. et al. Active deformation fields: Dense deformation field estimation for atlas-based segmentation using the active contour framework. _Medical Image Analysis_ 15, 787–800, doi:

http://dx.doi.org/10.1016/j.media.2011.05.008 (2011). Article  PubMed  Google Scholar  * Sdika, M. Combining atlas based segmentation and intensity classification with nearest neighbor

transform and accuracy weighted vote. _Medical Image Analysis_ 14, 219–226, doi: http://dx.doi.org/10.1016/j.media.2009.12.004 (2010). Article  PubMed  Google Scholar  * Heckemann, R. A.,

Hajnal, J. V., Aljabar, P., Rueckert, D. & Hammers, A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. _Neuroimage_ 33, 115–126, doi:

10.1016/j.neuroimage.2006.05.061 (2006). Article  PubMed  Google Scholar  * Klein, S. et al. Automatic segmentation of the prostate in 3D MR images by atlas matching using localized mutual

information. _Med Phys_ 35, 1407–1417 (2008). Article  PubMed  Google Scholar  * Cabezas, M., Oliver, A., Llado, X., Freixenet, J. & Cuadra, M. B. A review of atlas-based segmentation

for magnetic resonance brain images. _Comput Methods Programs Biomed_ 104, e158–177, doi: doi: 10.1016/j.cmpb.2011.07.015 (2011). Article  PubMed  Google Scholar  * Wu, G. et al. A

generative probability model of joint label fusion for multi-atlas based brain segmentation. _Med Image Anal_ 18, 881–890, doi: 10.1016/j.media.2013.10.013 (2014). Article  PubMed  Google

Scholar  * Asman, A. J. & Landman, B. A. Formulating spatially varying performance in the statistical fusion framework. _IEEE Trans Med Imaging_ 31, 1326–1336, doi:

10.1109/TMI.2012.2190992 (2012). Article  PubMed  PubMed Central  Google Scholar  * Coupe, P. et al. Patch-based segmentation using expert priors: application to hippocampus and ventricle

segmentation. _Neuroimage_ 54, 940–954, doi: 10.1016/j.neuroimage.2010.09.018 (2011). Article  PubMed  Google Scholar  * Fritscher, K. D. et al. Automatic segmentation of head and neck CT

images for radiotherapy treatment planning using multiple atlases, statistical appearance models, and geodesic active contours. _Med Phys_ 41, 051910, doi: 10.1118/1.4871623 (2014). Article

  PubMed  PubMed Central  Google Scholar  * Khan, A. R. et al. Optimal weights for local multi-atlas fusion using supervised learning and dynamic information (SuperDyn): Validation on

hippocampus segmentation. _Neuroimage_ 56, 126–139, doi: http://dx.doi.org/10.1016/j.neuroimage.2011.01.078 (2011). Article  PubMed  Google Scholar  * Zhang, S., Zhan, Y. & Metaxas, D.

N. Deformable segmentation via sparse representation and dictionary learning. _Medical Image Analysis_ 16, 1385–1396 (2012). Article  PubMed  Google Scholar  * Pipitone, J. et al.

Multi-atlas segmentation of the whole hippocampus and subfields using multiple automatically generated templates. _Neuroimage_ 101, 494–512, doi: 10.1016/j.neuroimage.2014.04.054 (2014).

Article  PubMed  Google Scholar  * Huang, M. et al. Brain extraction based on locally linear representation-based classification. _Neuroimage_ 92, 322–339, doi:

10.1016/j.neuroimage.2014.01.059 (2014). Article  PubMed  Google Scholar  * Warfield, S. K., Zou, K. H. & Wells, W. M. Simultaneous truth and performance level estimation (STAPLE): an

algorithm for the validation of image segmentation. _IEEE Trans Med Imaging_ 23, 903–921, doi: 10.1109/TMI.2004.828354 (2004). Article  PubMed  PubMed Central  Google Scholar  * Eskildsen,

S. F. et al. BEaST: brain extraction based on nonlocal segmentation technique. _Neuroimage_ 59, 2362–2373, doi: 10.1016/j.neuroimage.2011.09.012 (2012). Article  PubMed  Google Scholar  *

Pang, S. et al. In Patch-Based Techniques in Medical Imaging: First International Workshop, Patch-MI 2015, Held in Conjunction with MICCAI 2015, Munich, Germany, October 9, 2015, Revised

Selected Papers (eds Guorong Wu et al.) 104–111 (Springer International Publishing, 2015). * Sabuncu, M. R., Yeo, B. T., Van Leemput, K., Fischl, B. & Golland, P. A generative model for

image segmentation based on label fusion. _IEEE Trans Med Imaging_ 29, 1714–1729, doi: 10.1109/TMI.2010.2050897 (2010). Article  PubMed  PubMed Central  Google Scholar  * Langerak, T. R. et

al. Label fusion in atlas-based segmentation using a selective and iterative method for performance level estimation (SIMPLE). _IEEE Trans Med Imaging_ 29, 2000–2008, doi:

10.1109/TMI.2010.2057442 (2010). Article  PubMed  Google Scholar  * Roweis, S. T. & Saul, L. K. Nonlinear dimensionality reduction by locally linear embedding. _Science_ 290, 2323–2326,

doi: 10.1126/science.290.5500.2323 (2000). Article  CAS  ADS  PubMed  Google Scholar  * Zhang, P., Wee, C. Y., Niethammer, M., Shen, D. & Yap, P. T. Large deformation image

classification using generalized locality-constrained linear coding. _Med Image Comput Comput Assist Interv_ 16, 292–299 (2013). PubMed  PubMed Central  Google Scholar  * Wu, Y. et al.

Prostate segmentation based on variant scale patch and local independent projection. _IEEE Trans Med Imaging_ 33, 1290–1303, doi: 10.1109/TMI.2014.2308901 (2014). Article  ADS  PubMed 

Google Scholar  * Tibshrani, R. Regression shrinkage and selection via the LASSO. _Journal of the Royal Statistical Society_ 58, 267–288 (1996). MathSciNet  Google Scholar  * Wang, J. et al.

Locality-constrained linear coding for image classification. In _2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2010_). 3360–3367 (IEEE). * Liu, W., He, J. &

Chang, S.-F. Large graph construction for scalable semi-supervised learning. in _Proceedings of the 27th international conference on machine learning (ICML-10_). 679–686 (2010). * Smith, S.

M. Fast robust automated brain extraction. _Hum Brain Mapp_ 17, 143–155, doi: 10.1002/hbm.10062 (2002). Article  PubMed  PubMed Central  Google Scholar  * Tustison, N. J. et al. N4ITK:

improved N3 bias correction. _IEEE Trans Med Imaging_ 29, 1310–1320, doi: 10.1109/TMI.2010.2046908 (2010). Article  PubMed  PubMed Central  Google Scholar  * Ou, Y., Sotiras, A., Paragios,

N. & Davatzikos, C. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. _Med Image Anal_ 15, 622–639, doi: 10.1016/j.media.2010.07.002 (2011). Article 

PubMed  Google Scholar  * Smith, S. M. et al. Advances in functional and structural MR image analysis and implementation as FSL. _Neuroimage_ 23 Suppl 1, S208–219, doi:

10.1016/j.neuroimage.2004.07.051 (2004). Article  PubMed  Google Scholar  * Maurer, C. R., Qi, R. & Raghavan, V. A Linear Time Algorithm for Computing Exact Euclidean Distance Transforms

of Binary Images in Arbitrary Dimensions. _Pattern Analysis & Machine Intelligence IEEE Transactions on_ 25, 265–270 (2003). Article  Google Scholar  * Wu, Y. et al. Prediction of CT

Substitutes from MR Images Based on Local Diffeomorphic Mapping for Brain PET Attenuation Correction. _J Nucl Med_ 57, 1635–1641, doi: 10.2967/jnumed.115.163121 (2016). Article  PubMed 

Google Scholar  * Chen, Y. et al. Nonlocal prior Bayesian tomographic reconstruction. _J Math Imaging Vis_ 30, 133–146, doi: 10.1007/s10851-007-0042-5 (2008). Article  CAS  Google Scholar  *

Chen, Y. et al. Artifact Suppressed Dictionary Learning for Low-Dose CT Image Processing. _Ieee T Med Imaging_ 33, 2271–2292, doi: 10.1109/Tmi.2014.2336860 (2014). Article  Google Scholar 

Download references ACKNOWLEDGEMENTS This work was supported by the grants from National Natural Science Foundation of China (NSFC, Nos 61471187, and 31371009), the Science and Technology

Project of Guangdong Province (NO. 2015B010131011), the Program of Pearl River Young Talents of Science and Technology in Guangzhou (No. 2013J2200065), the Guangdong Natural Science

Foundation (No. 2014A030313316), and the Pearl River S&T Nova Program of Guangzhou (No. 2012J2200041). AUTHOR INFORMATION Author notes * Shumao Pang and Jun Jiang: These authors

contributed equally to this work. AUTHORS AND AFFILIATIONS * Guangdong Provincial Key Laboratory of Medical Image Processing, School of Biomedical Engineering, Southern Medical University,

Guangzhou, 510515, China Shumao Pang, Zhentai Lu, Xueli Li, Wei Yang, Meiyan Huang, Yu Zhang, Yanqiu Feng & Qianjin Feng * School of Basic Medical Science, Southern Medical University,

Guangzhou, 510515, China Jun Jiang & Wenhua Huang Authors * Shumao Pang View author publications You can also search for this author inPubMed Google Scholar * Jun Jiang View author

publications You can also search for this author inPubMed Google Scholar * Zhentai Lu View author publications You can also search for this author inPubMed Google Scholar * Xueli Li View

author publications You can also search for this author inPubMed Google Scholar * Wei Yang View author publications You can also search for this author inPubMed Google Scholar * Meiyan Huang

View author publications You can also search for this author inPubMed Google Scholar * Yu Zhang View author publications You can also search for this author inPubMed Google Scholar * Yanqiu

Feng View author publications You can also search for this author inPubMed Google Scholar * Wenhua Huang View author publications You can also search for this author inPubMed Google Scholar

* Qianjin Feng View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.P., Z.L. and Q.F. wrote the main manuscript text, S.P., J.J. and Z.L. did

the whole experiments, X.L., M.H. and Y.Z. drew all the figures, W.Y. and Y.F. revised the manuscript text, W.H. conducted the evaluation of the segmentation results. All authors reviewed

the manuscript. CORRESPONDING AUTHOR Correspondence to Qianjin Feng. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This

work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons

license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to

reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Pang, S., Jiang, J.,

Lu, Z. _et al._ Hippocampus Segmentation Based on Local Linear Mapping. _Sci Rep_ 7, 45501 (2017). https://doi.org/10.1038/srep45501 Download citation * Received: 21 October 2016 * Accepted:

01 March 2017 * Published: 03 April 2017 * DOI: https://doi.org/10.1038/srep45501 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative