Universal quantum gates for hybrid system assisted by atomic ensembles embedded in double-sided optical cavities

ABSTRACT We propose deterministic schemes for controlled-NOT (CNOT), Toffoli, and Fredkin gates between flying photon qubits and the collective spin wave (magnon) of an atomic ensemble

inside double-sided optical microcavities. All the gates can be accomplished with 100% success probability in principle and no additional qubit is required. Atomic ensemble is employed so

that light-matter coupling is remarkably improved by collective enhancement. We qualified the performance of the gates and the results show that they can be faithfully constituted with

current experimental techniques. SIMILAR CONTENT BEING VIEWED BY OTHERS CREATION OF GREENBERGER-HORNE-ZEILINGER STATES WITH THOUSANDS OF ATOMS BY ENTANGLEMENT AMPLIFICATION Article Open

access 05 February 2021 HAMILTONIAN ENGINEERING OF COLLECTIVE XYZ SPIN MODELS IN AN OPTICAL CAVITY Article 15 April 2025 SINGLE-MODE QUANTUM NON-GAUSSIAN LIGHT FROM WARM ATOMS Article Open

access 26 October 2022 INTRODUCTION Quantum logic gates usually lie at the heart of quantum-information processing (QIP) tasks. As is well known, any _n_-qubit quantum operation can be

decomposed into combinations of two-qubit gates and single-qubit operations1. So far, it has been well solved for the optimal synthesis of two-qubit gates, while it is more complex and still

an open question for the case of multi-qubit systems. So it is of significance to find a simpler way for directly implementing multi-qubit gates. On the other hand, Toffoli and Fredkin

gates are fundamental quantum gate for three-qubit systems, and they have attracted much attention since they can form a universal quantum computation architecture together with single-qubit

operations2,3,4,5,6,7. Moreover, they play an important role in quantum algorithms8, entanglement concentration and purification9,10,11, error correction12, and fault-tolerant quantum

circuits13. Many proposals have been proposed to implement quantum logic gates with several physical systems theoretically and experimentally, such as the ion trap14, nuclear magnetic

resonance15,16, quantum dot (QD)17,18,19, superconducting qubits20,21, nitrogen-vacancy (NV) centers22,23, and photon systems24,25. For scalable quantum computation and QIP, quantum gates

between two separated quantum nodes are indispensable. So far, one convenient way to realize such gates is to use linked cavities, each of which contains single or several qubits in it. To

constitute the critical two-qubit optical gate in a deterministic way, one can resort to Kerr nonlinearities. However, they are many orders of magnitude too small for efficient quantum

computation for naturally occurring nonlinearities in the single-photon level26. Several proposals based on Kerr nonlinearities in fibers or crystals27, electromagnetically induced

transparency22,28,29,30, and optical dipole-cavity system31,32 are developed. In the past decades, cavity quantum electrodynamics (cavity QED) that studies the coherent interaction of matter

with quantized fields has been a paradigm for QIP due to controllable interactions between dipole and photons31,33. As for the cavity-based scheme, the dipole embedded in the optical cavity

interacts strongly with the input single photons, and the interaction between the dipole and the successive photons provides strong Kerr nonlinearities17,18,31,34. In 2004, Duan _et al_.31

proposed a scheme for scalable photonic quantum computation based on cavity-assisted interaction between single-photon pulses. In 2005, Cho _et al_.32 proposed a scheme to implement a

two-qubit controlled-phase gate for single atomic qubits based on the cavity input-output process. Based on a singly charged QD inside an optical resonant cavity, several schemes for

entanglement generation and implementing of quantum logic gates are proposed17,18,19. Assisted with single photons, Zhou _et al_.35 provided the optimal approach to detect nonlocal atomic

entanglement. On the other hand, based on the photonic Faraday rotation, they also described the complete logic Bell-state analysis36. With the dipole induced transparency of a diamond NV

center, universal hyperparallel hybrid photonic quantum logic gates were proposed in 201522. Recently, an magnon-cavity unit, e.g., an atomic ensemble confined in a double-sided cavity, was

proposed by Li _et al_.34, in which the interaction between the collective spin wave (magnon) of an atomic ensemble and the successive photons provides strong Kerr nonlinearities. In this

paper, inspired by the above works, we investigate the possibility of achieving scalable photonic quantum computation assisted by an atomic ensemble in a double-sided cavity. Our schemes are

different from the work by Li _et al_.34 in which they present a scheme for two CNOT gates with the photonic qubits both in the spatial degrees of freedom (DOF) and the polarization DOF of

each photon. By the nonlinear interaction between the moving photon and the magnon of an atomic ensemble in a double-sided cavity, we first present a deterministic scheme for constructing a

CNOT gate on a hybrid system with the flying photon as the control qubit and the atomic ensemble as the target qubit. Besides, we construct the Toffoli and Fredkin gates on a three-qubit

hybrid system in a deterministic way. In our work, the control qubit of our universal gates is encoded on the polarization states of the moving photon, while the target qubit is encoded on

the state of atomic ensemble inside an optical microcavity. These three schemes for the universal gates require no additional qubit, and they only need some linear optical elements besides

Kerr nonlinear interaction between the magnon and the photons. High fidelities and high efficiencies can be achieved in the strong coupling regime and are not sensitive to the frequency

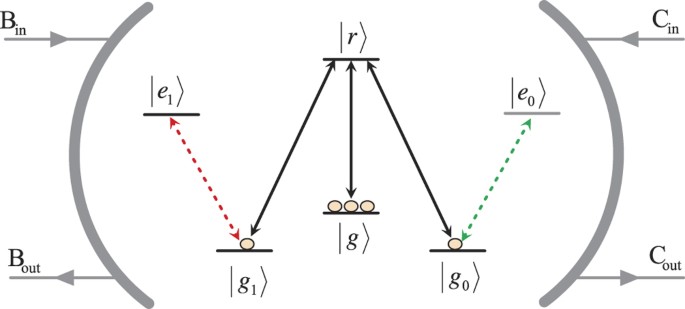
detuning and coupling imbalance. RESULTS INPUT-OUTPUT RELATION FOR A SINGLE PHOTON WITH A MAGNON-CAVITY COUPLING SYSTEM The configuration of the atomic ensemble cavity coupling system

considered here is exhibited schematically in Fig. 1. We first denote a highly excited Rydberg state as |_r_〉. Assisted by the Rydberg state |_r_〉, one can prepare the atomic ensemble into

the magnon state and perform the single-qubit operation on the magnon qubit. A qubit is encoded in collective spin wave state or magnon state with a single atom in the states |_g_0〉 and

|_g_1〉 of the atomic ensemble. If we define (_j_ = 0, 1), we have , where are the collective angular momentum operators with , and . The transitions and with frequency _ω_0 are driven by

orthogonal polarizations (_H_ and _V_) of a photon with frequency _ω_. Meanwhile the two transitions are nearly resonantly coupled to the two degenerate cavity modes and with the

corresponding coupling rates are _λ_0 and _λ_1, respectively. For the input photons with different polarizations, the transmission and reflection coefficients are determined by the state of

the ensemble. If a polarized photon is injected into the cavity via either side of the cavity, it will pass through the cavity if it is decoupled from the driven cavity mode; otherwise it

will interact with the atomic ensemble if it is coupled to the cavity mode and lead to the mode splitting. When the frequencies of the optical fields close to the cavity frequency _ω__a_, we

can take the coupling rates between an asymmetrical cavity and modes and of ports _B_ and _C_ as real constant31. Here, to insure the photon pulse shape remains unchanged, we need a single

polarized photon pulse with a finite bandwidth ([, ]), which is satisfied when (the cavity decay rate)17,18. If we take _ω__a_ as the carrier frequency, then _δ_′ = _ω_ − _ω__a_ denotes the

frequency detuning of the input photon with frequency _ω. δ_0 = _ω_0 − _ω__a_ measures the frequency difference between the dipole transition and the cavity mode. This system exhibits

similar features with the Jaynes-Cummings model, and in the frame rotating with respect to _ω__a_, the dynamics of the system is governed by the following hamiltonian (_ħ_ = 1)31,33,37 here

and _λ__j_ denote the spontaneous emission rate of the single excited collective state and the coupling rate between the atomic ensemble and the corresponding resonant cavity mode,

respectively. With the help of Rydberg state38,39 or coherent Raman process40,41, one can pump the atomic ensemble to the magnon state , so that the input photon will drive the interaction

between the atomic ensemble and the cavity mode. In the single excitation subspace, the system will evolve in the space spanned by the internal states of the atomic ensemble and the photon

number states of the radiation modes (, , and ), respectively. Suppose the initial state of the system is , i.e., we choose the input photon in mode , then the state of the system, at time

_t_, will evolve to The Schrödinger equation for this system can be specified to be Along with the standard input-output relation (_y_ = _b, c_), we can see the birefringent character of the

magnon-cavity system. Here and are the input and output field operators, respectively. Under the condition that the incoming field is very weak, i.e., we take , the reflection and

transmission coefficients of the system can be expressed as In the case the input photons uncoupled to the cavity, i.e., _λ__j_ = 0, we get the reflection and transmission coefficients for

the system, then Eq. (4) reduces to As the backscattering is low in the optical fibers, the asymmetry of the two coupling constants is mainly caused by cavity intrinsic loss42. Suppose (),

i.e., the difference of the coupling rates between the cavity and the modes and are small, one can replace the reflection and transmission coefficients above for the asymmetrical cavity

system with those for the symmetrical one with identical coupling rates, i.e., we set _κ_ = _κ__b_ = _κ__c_. With the symmetrical cavity, the corresponding reflection and transmission

coefficients can be respectively simplified and given by for _λ_ > 0 (hot cavity), and for _λ_ = 0 (cold cavity, described with the subscript 0). The reflection and transmission

coefficients in Eqs (6) and (7) indicate that the output photon experiences a phase shift relying on the different states of the atomic ensemble in the double-sided cavity. When the Purcell

factor _λ_2/_κγ_ = 1/2, the reflection and transmission coefficients are _r_(_ω_) → 1 and _t_(_ω_) → 0. However, in the decoupling case (_λ_ = 0), the reflection and transmission

coefficients of the bare cavity are _r_0(_ω_) → 0 and _t_0(_ω_) → −1. Specifically, if the atomic ensemble is in the state , when the photon in |_H_〉 (|_V_〉) state is directed into the

cavity, it will be reflected and get no phase shift. Otherwise, the photon will transmit the cavity and get a _π_ phase shift. This exactly demonstrates the effective Kerr nonlinearity which

can be used to constitute the hybrid multi-qubit gates in the following sections. CNOT GATE ON A TWO-QUBIT HYBRID SYSTEM The framework of our CNOT gate, which flips the target atomic

ensemble qubit if the control photon polarization qubit is in the state |_V_〉, is depicted in Fig. 2. The flying photon _p_ and the atomic ensemble are prepared in arbitrary superposition

states and (here ), respectively. For conciseness, we define single-qubit Hadamard operations H_p_ and H_s_ for one photon and one magnon qubit respectively as: First, the injected photon

passes through a polarized beam splitter (PBS1), which transmits the photon in the polarization state |_H_〉 and reflects the photon in the state |_V_〉. The part in the state |_H_〉 transmits

PBS1 and gets into a delay line (DL), does not interact with the cavity, while the part in the state |_V_〉 passes a half-wave plate (HWP1), which is used to perform a Hadamard operation

(H_p_) on the photon. Then the photon passes a beam splitter (BS) and be injected into the cavity from either path _a_1 or _a_2. At the same time, we perform a Hadamard operation (H_s_) on

the atomic ensemble with the coherent Raman process or Rydberg-state-assisted quantum rotation. Then the state of the whole system composed of a photon and an atomic ensemble is changed from

to . Here and Considering the birefringent propagation of the input polarized photon, the output state of photon together with that of the atomic ensemble is When the photon _p_ passes

through path _a_1, it will be split by PBS2, the _H_-polarized component takes a phase shift _π_ (i.e., |_H_〉 → −|_H_〉) after passing through the phase shifter _P__π_. Then the photon passes

PBS3 will take an H_p_ operation by HWP3. Meanwhile the photon passes through path _a_2 will take an H_p_ operation by HWP2. After the photon passes through PBS4 and HWP4, the state of the

system becomes Then we apply an H_s_ operation on the atomic ensemble, the state of the hybrid system becomes One can see that the state of the atomic ensemble is flipped when the photon

(the control qubit) is in the state |_V_〉, while it does not change when the photon is in the state |_H_〉, compared to the original state of the two-qubit hybrid system shown in Eq. (10).

Therefore, the quantum circuit shown in Fig. 2 can be used to construct a deterministic CNOT gate with a success probability of 100% in principle by using the photon as the control qubit and

the atomic ensemble as the target qubit. TOFFOLI GATE ON A THREE-QUBIT HYBRID SYSTEM The schematic diagram for implementing a deterministic three-qubit Toffoli gate is depicted in Fig. 3,

which performs a NOT operation on the second atomic ensemble (the target qubit) if and only if the photon is in the state |_V_〉 and the first atomic ensemble is in the state . Suppose that

the flying photon qubit is prepared in an arbitrary superposition state, , and each of the two independent atomic ensembles in cavities 1 and 2 is prepared in an arbitrary state as and .

Here . First the photon reaches PBS1, the photon in the state |_V_〉 is injected into the cavity from path _a_2, while the photon in the state |_H_〉 does not interact with the atomic ensemble

inside the cavity. With the same arguments as made for the CNOT gate above, we find that after the photon interacts with the atomic ensemble inside cavity 1, the state of the whole system

evolves from to . And Then the photon from path _a_1 goes into a DL, while the photon from path _a_2 passes HWP1 and BS, and then gets into cavity 2 from path _a_1 or _a_2. Meanwhile we

apply an H_s_ operation on the atomic ensemble in cavity 2. Considering the interaction between the photon and the atomic ensemble in cavity 2, we find the state of the system evolves from

to , here After the photon passes the channel combination module (CCM), we perform an H_s_ operation on the atomic ensemble in cavity 2 again, then the state of the combined system becomes

After the photon passes through the CCM, it is led back to cavity 1 from path , at the same time we lead the photon in path _a_1 into cavity 1 again (see the green lines), then the state of

the system evolves into After the photon reaches PBS2, we can see that the state of the target magnon qubit in cavity 2 is flipped when the two control photonic qubit and the magnon qubit in

cavity 1 are in the state |_V_〉 and , respectively. Therefore the quantum circuit shown in Fig. 3 can be used to construct a Toffoli gate on a photon-magnon hybrid system in a deterministic

way. FREDKIN GATE ON A THREE-QUBIT HYBRID SYSTEM The three-qubit Fredkin gate implements a swap operation on two stationary atomic ensemble qubits in cavities 1 and 2 when the flying photon

is in the state |_V_〉. Suppose that the initial states of the flying photon and the two atomic ensembles confined in the two double-sided cavities are And . As illustrated in Fig. 4, our

scheme for a three-qubit Fredkin gate can be achieved with three steps. _Step 1_. The injected photon is split by PBS1 into two wave-packets, the photon in state |_H_〉 dose not interact with

the atomic ensemble in cavity 1, while the photon in state |_V_〉 goes into path 2 and experiences the nonlinearities (see the green lines). After the photon in the state |_V_〉 is injected

into cavity 1, the state of the three-qubit hybrid system changes to After the photon interacts with the atomic ensemble inside cavity 1, it emits from path 3 or 4 and then be led into

cavity 2. After the photon interacts with the atomic ensemble inside cavity 2, becomes It can be seen that, when the photon in |_V_〉 passes through the two cavities in succession, the output

path of the photon is determined by the parity of the two magnon qubits. _Step 2_. The photon at S will be led to path 8, while the photon emitting from path 6 be led into cavity 1 again.

As discussed above, in this round, the photon in path 6 acts as the control qubit and performs NOT operations on the magnon qubits in cavities 1 and 2, respectively (see the grey lines,

i.e., HWP1 → BS1 → H_s_1 → Cavity1 → CCM1 → H_s_1 → HWP2 → BS2 → H_s_2 → Cavity2 → CCM2 → H_s_2). For this purpose, H_s_ operations on the atomic ensembles in cavities 1 and 2 before and

after the photon interacts with the corresponding magnon qubit respectively are needed. When the photon emits from path 7, the output state of the system is _Step 3_. In this round, the

photon emitting from path 7 or 8 will be led into cavities 1 and 2 successively again. As discussed in _step 1_, after the photon interacts with cavity 2 again, the state of the system

evolves into After this round, the photon emitting from path 5 will pass through S and reach PBS2. After the photon from path 1 or path 9 reaches PBS2, evolves into , From Eq. (24), one can

see that the states of the two solidstate target qubits (the two atomic ensembles in cavities 1 and 2) are swapped when the photon qubit is in the state |_V_〉, while they do not swap when

the photon qubit is in the state |_H_〉. The quantum circuit shown in Fig. 4 can be used to construct the Fredkin gate on a three-qubit hybrid system in a deterministic way. DISCUSSION The

key ingredient in our scheme is the combined magnon-cavity unit, such a system is a promising candidate for QIP since the birefringent propagation of the successively input photons acts as

the effective Kerr nonlinearity. In this section, We quantitatively characterize the fidelities and efficiencies of our hybrid gates, respectively. The fidelity of our Fredkin gate with

respect to normalized photon detuning Δ/_κ_ and the coupling rate _λ_/_κ_ are shown in Fig. 5 when _γ_ = _κ_. In principle, the detuning Δ/_κ_ can be arbitrarily reduced, if the input photon

is tuned to be resonant to the cavity, and then one has _F__F_ = 97.2% when _γ_ = _κ_ and _λ_/_κ_ = 3; while when photon detuning and , one has . The fidelity _F__F_ approaches a steady

value limited by the frequency detuning . The efficiencies of our universal quantum gates are shown in Fig. 6 when setting _γ_ = _κ_. For Δ = 0, _γ_ = _κ_ and , , , ; while when photon

detuning and , one has , , . We can see that the performance of our universal quantum gates, to some extent, are not sensitive to the detuning Δ and get better when the coupling rate _λ_/_κ_

increases. In fact, there might be some difference in the coupling rates between the cavity and modes and () in practice. In experiment, the difference of the two coupling constants has

been demonstrated, which yields approximately the same fidelity for both transmission and reflection directions42. In the resonant case (_ω__c_ = _ω_0 = _ω_), there will be an additional

error probability in the single-photon scattering process by . And this error can be improved for the cavity with almost identical mirrors43,44, which will lead to the ideal photon

blockade45. To discuss the sensitivity of our schemes to _κ_Δ, the fidelities and efficiencies of our gates are calculated with the similar procedure as those used in the symmetric case by

using the reflection and transmission coefficients obtained with the asymmetrical cavity. The fidelities and efficiencies of our gates are shown in Fig. 7, here we choose , _γ_ = _κ__b_ and

Δ = 0. When setting _λ_/_κ_ = 3, one has with , with and with . Compared with those in the symmetric case, the little decreases of the fidelities and efficiencies in the asymmetric case

prove that our universal quantum gates are robust to the cavity coupling imbalance. As reported in refs 46, 47, the maximum coupling strength between a single atom and a single intracavity

photon, along with the decay rate of the excited state and the cavity mode, are . Thereby we can see that our hybrid quantum gates are robust against the practical imperfections. Recently,

there have been plenty of other methods to couple an atomic ensemble with an optical cavity48,49, which might be another building block for our schemes. The fidelities of the spin wave

rotation procedures of 99% have been reported50, and the collective spin wave operations in atomic ensembles have been well developed51. Besides, the atomic ensembles can store photons in a

single atomic ensemble with several milliseconds52, so this manon-cavity unit is a good quantum memory system for photonic qubits, which is essential in scalable quantum networks. Therefore,

our hybrid quantum gates may be achieved with the current QED setup. In addition, our hybrid quantum gates are quite different from the previous ones based on the quantum dot embedded in

microcavities6,7 and those assisted by NV centers embedded in photonic crystal cavities coupled to two wave guides30. We use the atomic ensemble approach, so that light-matter coupling is

largely improved by collective enhancement53. The control qubit of our gates is encoded on the polarization of the moving single photon and the target qubits are encoded on the magnon states

of the atomic ensembles inside optical microcavities. As discussed in Sec. III, when the photon in |_V_〉 passes through the two cavities in succession, the output path of the photon is

determined by the parity of the two magnon qubits, this makes the present schemes more succinct than the previous schemes6. In addition, because they do not require that the transmission for

the uncoupled cavity is balanceable with the reflectance for the coupled cavity, our schemes are robust, this is different from the hybrid gates which are encoded on the atom confined in a

single-sided cavity18,31. CONCLUSION In conclusion, we have designed the compact quantum circuits for implementing deterministic universal hybrid quantum gates, including the CNOT, Toffoli,

and Fredkin gates, by means of the the effective Kerr nonlinearity induced by an atomic ensemble embedded in a double-sided cavity. The spontaneous emission and the cavity decay induce the

different transmittance or reflectance coefficients between the hot cavity and the cold cavity in a magnon-cavity system. We have shown the schemes are robust to the variation of coupling

rate _λ__j_ and the detuning Δ involved in the practical experiments. High fidelities and efficiencies can be achieved in the strong coupling regime in our schemes. We hope this work will be

useful in quantum computation and quantum networks with single photons. METHODS Under the ideal case, suppose that the optical elements, such as PBS, HWP, _P__π_, and optical switch, are

perfect, both the success probability and the fidelity of the present schemes are 100% in principle. For a practical magnon-cavity unit, the spontaneous emission of the collective states and

cavity decay may leading to photon loss, which will reduce the performance of our hybrid gates. THE FIDELITIES OF THE GATES We introduce the gate fidelity, which measures the distance for

quantum information, is defined as54 where is the input states, _U_ is the ideal CONT (Toffoli or Fredkin) gate, and , with being the final state after the realistic CONT (Toffoli or

Fredkin) operation in the present scheme. Considering the rules for optical transitions in a realistic cavity system, combing the arguments made in Sec. III, we find that the state of the

system described by Eq. (12) becomes The terms with underlines indicate the states which take the bit-flip error. Then, the fidelity of the CNOT gate can be written as Similarly, we can

calculate the fidelities for the Toffoli (_F__T_) and the Fredkin (_F__F_) gates discussed in Sec. III, respectively: Defining the efficiency of a quantum gate as the ratio of the number of

the outputting photons to the inputting photons. The reflection and transmission coefficients of the magnon-cavity system will modify the output states of the quantum gates. According to the

discussions made in Sec. III, the efficiencies of our gates can be written as with , , , and . EXPERIMENTAL REALIZATION OF AN ATOMIC ENSEMBLE CAVITY SYSTEM The physical configuration that

we consider in the present schemes can employ 87Rb55,56 atomic ensemble. In a real experiment, one can couple a Bose-Einstein condensate of 87Rb atomic ensemble to an optical Fabry-Perot

cavity46,47. We choose the two stable hyperfine ground states |_g_0〉 and |_g_1〉 as the (_F_ = 1, _M__F_ = −1) level and the (_F_ = 1, _M__F_ = 1) level of the 5_S_1/2 state, while two

metastable hyperfine excited states are the (_F_ = 2, _M__F_ = −2) level and the (_F_ = 2, _M__F_ = 2) level of 5_P_1/2. Meanwhile, a highly excited Rydberg state _nS_1/2 can be chosen as

|_r_〉. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Liu, A.-P. _et al_. Universal quantum gates for hybrid system assisted by atomic ensembles embedded in double-sided optical cavities.

_Sci. Rep._ 7, 43675; doi: 10.1038/srep43675 (2017). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. REFERENCES * Barenco, A. et al. Elementary gates for quantum computation. _Phys. Rev. A_ 52, 3457–3467 (1995). ADS  CAS  PubMed  Google Scholar  * Fredkin, E. & Toffoli, T.

Conservative logic. _Int. J. Theor. Phys._ 21, 219–253 (1982). MathSciNet  MATH  Google Scholar  * Shi, Y. Y. Both Toffoli and Controlled-NOT need little help to do universal quantum

computation. _Quantum Inf. Comput._ 3, 84 (2003). MathSciNet  MATH  Google Scholar  * Gasparoni, S., Pan, J. W., Walther, P., Rudolph, T. & Zeilinger, A. Realization of a photonic

controlled-NOT gate sufficient for quantum computation. _Phys. Rev. Lett._ 93, 020504 (2004). ADS  Google Scholar  * Fiurášek, J. Linear-optics quantum Toffoli and Fredkin gates. _Phys. Rev.

A_ 73, 062313 (2006). ADS  Google Scholar  * Wei, H. R. & Deng, F. G. Universal quantum gates for hybrid systems assisted by quantum dots inside double-sided optical microcavities.

_Phys. Rev. A_ 87, 022305 (2013). ADS  Google Scholar  * Wei, H. R. & Deng, F. G. Scalable photonic quantum computing assisted by quantum-dot spin in double-sided optical microcavity.

_Opt. Express_ 21, 17671–17685 (2013). ADS  PubMed  Google Scholar  * Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. _SIAM J.

Sci. Stat. Comput._ 26, 1484–1509 (1997). MathSciNet  MATH  Google Scholar  * Wang, C., Shen, W. W., Mi, S. C., Zhang, Y. & Wang, T. J. Concentration and distribution of entanglement

based on valley qubits system in graphene. _Sci. Bull._ 60, 2016–2021 (2015). CAS  Google Scholar  * Cao, C. et al. Concentrating partially entangled W-class states on nonlocal atoms using

low-Q optical cavity and linear optical elements. _Sci. China Phys. Mech. Astro._ 59, 100315 (2016). Google Scholar  * Sheng, Y. B., Zhao, S. Y., Liu, J. & Zhou, L. Atomic entanglement

purification using photonic Faraday rotation. _Quantum Inf. Process._ 13, 881–893 (2014). ADS  CAS  MATH  Google Scholar  * Cory, D. G. et al. Experimental quantum error correction. _Phys.

Rev. Lett._ 81, 2152 (1998). ADS  CAS  Google Scholar  * Dennis, E. Toward fault-tolerant quantum computation without concatenation. _Phys. Rev. A_ 63, 052314 (2001). ADS  Google Scholar  *

Liang, L. M. & Li, C. Z. Realization of quantum SWAP gate between flying and stationary qubits. _Phys. Rev. A_ 72, 024303 (2005). ADS  Google Scholar  * Chuang, I. L., Gershenfeld, N.,

Kubinec, M. G. & Leung, D. W. Bulk quantum computation with nuclear magnetic resonance: theory and experiment. _Proc. R. Soc. London, Ser. A_ 454, 447–467 (1998). ADS  CAS  MATH  Google

Scholar  * Feng, G. R., Xu, G. F. & Long, G. L. Experimental realization of nonadiabatic holonomic quantum computation. _Phys. Rev. Lett._ 110, 190501 (2013). ADS  Google Scholar  * Hu,

C. Y., Young, A., O’Brien, J. L., Munro, W. J. & Rarity, J. G. Deterministic photon entangler using a charged quantum dot inside a microcavity. _Phys. Rev. B_ 78, 085307 (2008). ADS 

Google Scholar  * Hu, C. Y., Munro, W. J., O’Brien, J. L. & Rarity, J. G. Proposed entanglement beam splitter using a quantum-dot spin in a double-sided optical microcavity. _Phys. Rev.

B_ 80, 205326 (2009). ADS  Google Scholar  * Bonato, C. et al. CNOT and Bell-state analysis in the weak-coupling cavity QED regime. _Phys. Rev. Lett._ 104, 160503 (2010). ADS  PubMed  Google

Scholar  * Niskanen, A. O., Vartiainen, J. J. & Salomaa, M. M. Optimal multiqubit operations for Josephson charge qubits. _Phys. Rev. Lett._ 90, 197901 (2003). ADS  PubMed  Google

Scholar  * Hua, M., Tao, M. J., Deng, F. G. & Long, G. L. One-step resonant controlledphase gate on distant transmon qutrits in different 1D superconducting resonators. _Sci. Rep._ 5,

14541 (2015). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ren, B. C., Wang, G. Y. & Deng, F. G. Universal hyperparallel hybrid photonic quantum gates with dipole-induced

transparency in the weak-coupling regime. _Phys. Rev. A_ 91, 032328 (2015). ADS  Google Scholar  * Liu, A. P. et al. Deterministic controlled-phase gate and SWAP gate with dipole-induced

transparency in the weak-coupling regime. _Opt. Commun._ 379, 19–24 (2016). ADS  CAS  Google Scholar  * Kok, P. et al. Linear optical quantum computing with photonic qubits. _Rev. Mod.

Phys._ 79, 135 (2007). ADS  CAS  Google Scholar  * Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. _Nature (London)_ 409, 46–52

(2001). ADS  CAS  Google Scholar  * Kok, P., Lee, H. & Dowling, J. P. Single-photon quantum-nondemolition detectors constructed with linear optics and projective measurements. _Phys.

Rev. A_ 66, 063814 (2002). ADS  Google Scholar  * Matsuda, N., Shimizu, R., Mitsumori, Y., Kosaka, H. & Edamatsu, K. Observation of optical-fibre Kerr nonlinearity at the single-photon

level. _Nat. Photon._ 3, 95–98 (2009). ADS  CAS  MATH  Google Scholar  * Friedler, I., Petrosyan, D., Fleischhauer, M. & Kurizki, G. Long-range interactions and entanglement of slow

single-photon pulses. _Phys. Rev. A_ 72, 043803 (2005). ADS  Google Scholar  * Sevincli, S., Henkel, N., Ates, C. & Pohl, T. Nonlocal nonlinear optics in cold Rydberg gases. _Phys. Rev.

Lett._ 107, 153001 (2011). ADS  CAS  PubMed  Google Scholar  * Wei, H. R. & Deng, F. G. Compact quantum gates on electron-spin qubits assisted by diamond nitrogen-vacancy centers inside

cavities. _Phys. Rev. A_ 88, 042323 (2013). ADS  Google Scholar  * Duan, L. M. & Kimble, H. J. Scalable photonic quantum computation through cavity-assisted interactions. _Phys. Rev.

Lett._ 92, 127902 (2004). ADS  Google Scholar  * Cho, J. & Lee, H. W. Generation of atomic cluster states through the cavity input-output process. _Phys. Rev. Lett._ 95, 160501 (2005).

ADS  PubMed  Google Scholar  * Chen, Q., Yang, W. L., Feng, M. & Du, J. F. Entangling separate nitrogen-vacancy centers in a scalable fashion via coupling to microtoroidal resonators.

_Phys. Rev. A_ 83, 054305 (2011). ADS  Google Scholar  * Li, T. & Long, G. L. Hyperparallel optical quantum computation assisted by atomic ensembles embedded in double-sided optical

cavities. _Phys. Rev. A_ 94, 022343 (2016). ADS  Google Scholar  * Zhou, L. & Sheng, Y. B. Detection of nonlocal atomic entanglement assisted by single photons. _Phys. Rev. A_ 90, 024301

(2014). ADS  Google Scholar  * Zhou, L. & Sheng, Y. B. Complete logic Bell-state analysis assisted with photonic Faraday rotation. _Phys. Rev. A_ 92, 042314 (2015). ADS  Google Scholar

  * An, J. H., Feng, M. & Oh, C. H. Quantum-information processing with a single photon by an input-output process with respect to low-Q cavities. _Phys. Rev. A_ 79, 032303 (2009). ADS 

Google Scholar  * Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. _Rev. Mod. Phys._ 82, 2313 (2010). ADS  CAS  Google Scholar  * Mei, F., Feng, M., Yu, Y.

F. & Zhang, Z. M. Scalable quantum information processing with atomic ensembles and flying photons. _Phys. Rev. A_ 80, 042319 (2009). ADS  Google Scholar  * Li, S. et al. Coherent

manipulation of spin-wave vector for polarization of photons in an atomic ensemble. _Phys. Rev. A_ 84, 043430 (2011). ADS  Google Scholar  * Böhi, P. et al. Coherent manipulation of

Bose-Einstein condensates with state-dependent microwave potentials on an atom chip. _Nat. Phys._ 5, 592–597 (2009). Google Scholar  * O’Shea, D., Junge, C., Volz, J. & Rauschenbeutel,

A. Fiber-optical switch controlled by a single atom. _Phys. Rev. Lett._ 111, 193601 (2013). ADS  PubMed  Google Scholar  * Muller, A., Flagg, E. B., Lawall, J. R. & Solomon, G. S.

Ultrahigh-finesse, low-mode-volume Fabry-Perot microcavity. _Opt. Lett._ 35, 2293–2295 (2010). ADS  CAS  PubMed  Google Scholar  * Biedermann, G. et al. Ultrasmooth microfabricated mirrors

for quantum information. _Appl. Phys. Lett._ 97, 181110 (2010). ADS  Google Scholar  * Birnbaum, K. M. et al. Photon blockade in an optical cavity with one trapped atom. _Nature (London)_

436, 87–90 (2005). ADS  CAS  Google Scholar  * Brennecke, F. et al. Cavity QED with a Bose-Einstein condensate. _Nature (London)_ 450, 268–271 (2007). ADS  CAS  Google Scholar  * Brennecke,

F., Ritter, S., Donner, T. & Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. _Science_ 322, 235–238 (2008). ADS  CAS  PubMed  Google Scholar  * Ritsch, H., Domokos,

P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. _Rev. Mod. Phys._ 85, 553 (2013). ADS  CAS  Google Scholar  * Chen, Q., Yang, W. L. &

Feng, M. Controllable quantum state transfer and entanglement generation between distant nitrogen-vacancy-center ensembles coupled to superconducting flux qubits. _Phys. Rev. A_ 86, 022327

(2012). ADS  Google Scholar  * Rui, J. et al. Operating spin echo in the quantum regime for an atomic-ensemble quantum memory. _Phys. Rev. Lett._ 115, 133002 (2015). ADS  PubMed  Google

Scholar  * Xu, Z., Wu, Y., Liu, H., Li, S. & Wang, H. Fast manipulation of spin-wave excitations in an atomic ensemble. _Phys. Rev. A_ 88, 013423 (2013). ADS  Google Scholar  * Lvovsky,

A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. _Nat. Photon._ 3, 706–714 (2009). ADS  CAS  Google Scholar  * Gorshkov, A. V., André, A., Fleischhauer, M., Sørensen, A. S.

& Lukin, M. D. Universal approach to optimal photon storage in atomic media. _Phys. Rev. Lett._ 98, 123601 (2007). ADS  PubMed  Google Scholar  * Poyatos, J. F., Cirac, J. I. &

Zoller, P. Complete characterization of a quantum process: the two-bit quantum gate. _Phys. Rev. Lett._ 78, 390 (1997). ADS  CAS  Google Scholar  * Steck, D. A. Rubidium 87 D Line Data,

http://steck.us/alkalidata (revision 2.1.4, 23 December 2010). * Shih, C. Y. & Chapman, M. S. Nondestructive light-shift measurements of single atoms in optical dipole traps. _Phys. Rev.

A_ 87, 063408 (2013). ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This work is supported by the Doctoral Scientific Research Foundation of Shanxi Institute of Technology No.

201605002, and the National Natural Science Foundation of China under Grants No. 11604190 and No. 61465013. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Shanxi Institute of Technology,

Yangquan, 045000, Shanxi, China A.-Peng Liu & Ming-Xia Zhao * School of Physics and Information Engineering, Shanxi Normal University, Linfen, 041004, Shanxi, China Liu-Yong Cheng *

College of Physics and Electronics Engineering, Shanxi University, Taiyuan, 030006, Shanxi, China Qi Guo * Department of Physics, College of Science, Yanbian University, Yanji, 133002,

Jilin, China Shou Zhang Authors * A.-Peng Liu View author publications You can also search for this author inPubMed Google Scholar * Liu-Yong Cheng View author publications You can also

search for this author inPubMed Google Scholar * Qi Guo View author publications You can also search for this author inPubMed Google Scholar * Shou Zhang View author publications You can

also search for this author inPubMed Google Scholar * Ming-Xia Zhao View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.-P.L. and Q.G.

designed the schemes, L.-Y.C., M.-X.Z. and S.Z. carried out the theoretical analysis. All authors contributed to the interpretation of the work and the writing of the manuscript. All authors

reviewed the manuscript. CORRESPONDING AUTHORS Correspondence to A.-Peng Liu or Shou Zhang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests.

RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the

article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission

from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Liu, AP., Cheng, LY., Guo, Q. _et al._ Universal quantum gates for hybrid system assisted by atomic ensembles embedded in double-sided optical cavities. _Sci Rep_ 7, 43675 (2017).

https://doi.org/10.1038/srep43675 Download citation * Received: 30 November 2016 * Accepted: 25 January 2017 * Published: 08 March 2017 * DOI: https://doi.org/10.1038/srep43675 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative