Polarization shaping of high-order harmonics in laser-aligned molecules

ABSTRACT The present work reports on the generation of short-pulse coherent extreme ultraviolet radiation of controlled polarization. The proposed strategy is based on high-order harmonics

generated in pre-aligned molecules. Field-free molecular alignment produced by a short linearly-polarized infrared laser pulse is used to break the isotropy of a gas medium. Driving the

aligned molecules by a circularly-polarized infrared pulse allows to transfer the anisotropy of the medium to the polarization of the generated harmonic light. The ellipticity of the latter

is controlled by adjusting the angular distribution of the molecules at the time they interact with the driving pulse. Extreme ultraviolet radiation produced with high degree of ellipticity

(close to circular) is demonstrated. SIMILAR CONTENT BEING VIEWED BY OTHERS ENABLING ELLIPTICALLY POLARIZED HIGH HARMONIC GENERATION WITH SHORT CROSS POLARIZED LASER PULSES Article Open

access 08 August 2023 ELLIPTICALLY POLARIZED HIGH-HARMONIC RADIATION FOR PRODUCTION OF ISOLATED ATTOSECOND PULSES Article Open access 05 May 2021 PROPAGATION OF OPTICALLY TUNABLE COHERENT

RADIATION IN A GAS OF POLAR MOLECULES Article Open access 19 October 2020 INTRODUCTION High-harmonic generation (HHG) by intense femtosecond laser pulses has been extensively investigated

for the last two decades1,2,3. The research accomplished in this field has led to the emergence of table-top sources of coherent bright, ultrashort extreme ultraviolet (EUV) and Soft X-ray

radiation and attosecond pulses4. The unique characteristics of these sources make them suitable for a wide range of applications, including time-resolved ultrafast dynamics in gas phase and

condensed matter4. Most of the studies and applications of HHG have been performed with linearly-polarized HHG, although there is a strong demand for providing harmonics with controllable

polarization-state. In particular, circularly-polarized short EUV pulses are very useful for investigating circular dichroism, ultrafast spin dynamics, magnetic microscopy, chirality

assignment, and so forth. Several theoretical methods have been proposed for generating circularly-polarized harmonics (see _e.g._ refs 5, 6, 7). However, experimental demonstrations were

still very limited until a couple of years ago and in all attempts the harmonic radiation were limited to low photon flux and/or poor ellipticity8,9,10,11. The past two years have seen the

emergence of noteworthy achievements that have overcome the previous limitations. This breakthrough was initiated by the work of Fleisher _et al_.12, where tunable polarization

high-harmonics were generated using coplanar, elliptically-polarized counter-rotating dichroic drivers. Based on a similar strategy, Kfir _et al_.13 were able to produce circularly-polarized

EUV light using circularly-polarized, instead of elliptically-polarized, counter-rotating dichroic drivers and provided the first application of EUV table-top source to the measurement of

magnetic circular dichroism (MCD) in thin CO foil enabling in the same way to determine the helicity of the produced circular EUV beam. Hickstein _et al_.14,15 pushed further the concept of

counter-rotating circularly-polarized laser pulses by showing that a non collinear geometry allows, among other advantages, the production of spatially separated circularly-polarized

harmonics of the same frequency and opposite helicity. In the mean time, photoelectron circular dichroism of chiral molecules using elliptically-polarized light combined with a resonant

interaction was reported by Ferré _et al_.16 and elliptically-polarized EUV light produced by crossed polarized phase quadrature dichroic fields allowed the measurement of the MCD effect of

nickel by Lambert _et al_.17. Following a different approach, we have shown that circularly-polarized light can be used to drive harmonic generation in aligned molecules18. Among other

potential applications, we presented results on controlling the polarization of the generated harmonic radiation. However, the analytical model presented in ref. 18 was developed in the

framework of perturbation theory and the experiment was carried out by detecting the third-harmonic radiation generated with a weak laser field. The purpose of the present report is to

demonstrate that aligned molecules driven by quasi circularly-polarized light, _i.e._, with an ellipticity set close to unity, can be used to produce elliptically- and circularly-polarized

higher-order harmonics generated in the strong field regime. The strategy presented here allows extensive control over the polarization of the generated radiation, complementing the existing

toolbox of polarization engineering of high harmonic EUV sources. RESULTS PRODUCTION AND ANALYZIS OF THE HARMONICS The experiment is based on a 10 Hz amplified Ti:sapphire femtosecond laser

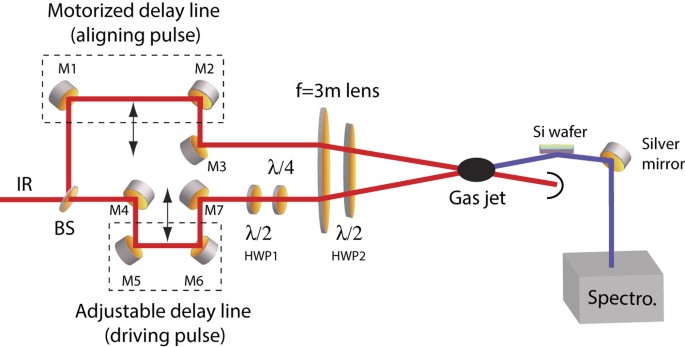
system delivering 30 fs pulse duration at _λ_0 = 800 nm with a maximum energy of 400 mJ. The whole experimental setup is designed so as to be operated under vacuum conditions. As depicted

in Fig. 1, the radiation of a Ti:sapphire fs laser system is split in two so as to provide a sequence of aligning and driving pulse with an adjustable time delay. The aligning pulse is

linearly polarized, whereas the second pulse driving the harmonic process can be circularly polarized using a combination of a half- (HWP1) and a quarter-wave (_λ_/4) plate. The two beams

are focused by a 3-meter focal length and crossed at a small angle into a pulsed jet of carbon dioxide (CO2) gas where the EUV radiations are generated. The intensity of the IR light on the

spectrometer is reduced by a silicon wafer working with an incidence angle of 75°, _i.e._, close to the Brewster angle for 800 nm. The harmonic radiation is then reflected by a silver

mirror, dispersed by an EUV spectrometer, and finally imaged on microchannel plates (MCP) detector. The back side of the MCP detector is mounted on a phosphor screen enabling recording the

harmonic spectrum with a CCD camera. The polarization of the harmonics is measured thanks to the combination of polarization sensitive optical elements including the Si wafer, the silver

mirror, and the grating of the spectrometer, the whole acting as a EUV reflective polarization analyzer favouring _s_-polarized waves. Since the HHG polarization measurements can not be

achieved by rotating the analyzer, the former is conducted by rotating both the aligning and the driving pulse around the optical axis using a large-aperture half-wave plate (HWP2) through

which both pulses are passing. In the results shown below, the energy of the aligning (driving) pulse is set to 10 mJ (15 mJ) leading to an estimated peak intensity at focus of ≈7 × 1013 

W/cm2 (≈1 × 1014 W/cm2). The characterization of the EUV analyzer is performed by recording the harmonic signal produced by randomly oriented CO2 molecules exposed to a linearly

_p_-polarized pulse. For symmetry reasons, the harmonics share the same polarization with the driving field. Although all angular distributions presented in this work have been recorded by

rotating the field to be analyzed with the aid of HWP2, for the sake of simplicity we will consider hereafter that the field is fixed whereas the analyzer is rotated. The latter is not

standard in so far as its extinction ratio _R_, defined here as the ratio between the detected signals for a linearly-polarized field oriented vertically (_i.e., s_-polarized) and

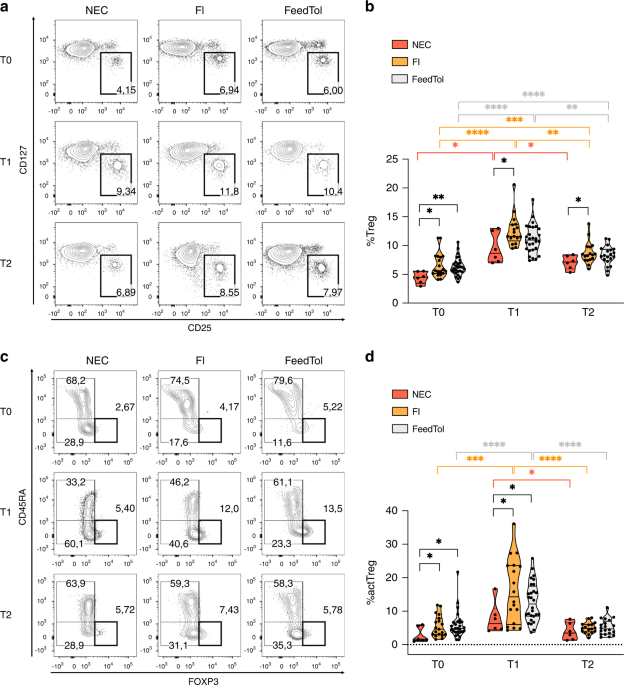
horizontally (_i.e., p_-polarized), is much smaller than what is currently obtained with traditional polarizers. Figure 2(a) depicts the signal of the 9th harmonic recorded over several

turns of HWP2. The angle Φ describes the orientation of the analyzer axis, defined here as the direction along which its efficiency is maximum, with respect to the horizontal axis. The same

signal depicted in a polar coordinates system is shown in Fig. 2(b). As shown, the horizontally polarized field leads to maxima when Φ = 0 [_π_]. An accurate determination of the contrast of

the analyser can be deduced from the modulation depth of the signal using a modified Malus’ Law whose details can be found in the Supplemental information online. The result of the

simulation performed with the fitted contrast value _R_ = 4.5 is shown for comparison in the same figures. POLARIZATION CONTROL OF HIGH-ORDER HARMONICS Next, we consider the possibility to

control the polarization of the generated harmonics. Before to address this matter, it should be mentioned that harmonic generation of circularly-polarized radiation is allowed in a gas of

aligned molecules. For reviews on laser-induced molecular alignment, see e.g., refs 19, 20. This has been demonstrated in the specific case of third-harmonic generation18. In a gas of atoms

or randomly oriented molecules, the harmonic generation process is forbidden due to the conservation of the spin angular momentum in “atom + field” or “molecule + field” systems presenting a

symmetry axis. In an ensemble of aligned molecules, the axial symmetry of the system can be broken if the propagation axis of the circularly-polarized field and the alignment axis are

different. In that case, the projection _m_ of the angular momentum _J_ along any axis is not longer a good quantum number. As a consequence, third-harmonic generation and higher-order

frequency up conversion processes are allowed. Figure 3 depicts for instance the 9th harmonic generated by a circularly-polarized IR pulse in CO2 molecules for different temporal delays

between the aligning and driving pulse. So far, this is the first report of HHG produced with a circularly-polarized field. The alignment field is linearly polarized within the polarization

plane of the driving field. The adjustment of the half-wave plate HWP1 with respect to the neutral axis of the quarter-wave plate (see Fig. 1) is performed so as to produce the extinction of

the harmonic signal in the absence of the aligning pulse. As a result of the anisotropy introduced by aligning the molecules, the harmonics generated by the circularly-polarized pulse

should be elliptically polarized, the ellipticity of them being governed by the time delay between the alignment pulse and the driving field. In order to verify this assumption, both

polarization components of the harmonic field must be resolved. Figure 4 (a) compares the harmonic signal recorded with two orthogonal orientations of the analyzer, namely vertical and

horizontal. The difference between the two curves reveals that the polarization of the harmonic field varies with the delay as a result of the change occurring in the angular distribution of

the molecules. In order to quantify the impact of these change, the polarization of the harmonic field is measured using the same methods as in Fig. 2. The result is shown in Fig. 4(b) for

a delay set at 11.2 ps. Using the contrast value _R_ determined before, the numerical model allows to estimate the ratio , with _E__y_ (_E__z_) the field component along the horizontal

_y_-axis (vertical _z_-axis), and _ϕ_ = _ϕ__y_ − _ϕ__z_ the dephasing between these components. The fitted value of the field component ratio (_r_ = 0.14) reveals that the polarization of

the field is closed to linear with an orientation along the _y_-axis (_i.e._, the _p_-wave is dominant). Because of the limited extinction ratio of the EUV analyzer, this small ellipticity

produces a signal that is about 3 times larger [see Fig. 4(a)] when the axis of the analyzer is oriented along the horizontal direction of the field as compared to the vertical one. For

comparison, an ideal analyzer would lead with the same field ellipticity to a contrast of about 50. The fitted value of the dephasing is _ϕ_ = 1.33 rad. The small deviation from the expected

value _π_/2, which remains within the experimental uncertainty, is responsible for a slight tilt of the angular distribution observed in the fitted curve of Fig. 4(b). From the

determination of _r_ and _ϕ_, the ellipticity of the EUV field defined as _ε_ = tan(1/2 arcsin[2_r/_(1 + _r_2) sin_ϕ_]) is estimated to 0.14. As a general remark, it should be pointed out

that _ε_ provides an upper value of the ellipticity since our detection scheme does not allow to differentiate polarized from unpolarized light. Some unpolarized EUV component may be present

due to the radial and temporal intensity variation of the lasers. However, due to the high nonlinearity of the harmonic generation process the most efficient generation results from the

highest laser intensity part, where the intensity distribution does not vary significantly and thus the unpolarized EUV component remains small. It is well known that the phase quadrature

between the two oscillating field components is a first prerequisite in achieving a circular polarization. The second one is that the components should share the same amplitude. In

principle, the latter can be obtained by adjusting the time delay so as to find a temporal domain where the two signals depicted in Fig. 4(a) are equal18. However, depending on the harmonic

order and the degree of alignment, the two field components are not necessarily balanced when the harmonic amplitude is significant. To circumvent this problem, a small ellipticity is

introduced along the horizontal or vertical direction of the driving field in order to increase the generation along the corresponding direction. This can be understood as analogous to the

addition of a small linear component to a circularly-polarized IR field, the former producing harmonics preferentially along its direction. This approach is applied to the result presented

in Fig. 5(a) where the half-wave plate HWP1 has been slightly tilted from the direction optimizing the suppression of the harmonic signal. The corresponding polarization analysis performed

at a delay of 11.2 ps is shown in Fig. 5(b). The ellipticity and phase value derived from the least square fit are _ε_ = 0.85 and _ϕ_ = 1.73 rad, respectively. Although the amplitude ratio

between the two field components is very close to unity (_r_ = 0.97), the small difference between the fitted phase and _π/2_ (+9°) generates a small ellipticity of the theoretical curve.

The polarization of Fig. 5(c) is obtained after a small shift of the delay, 11.18 ps, and with a different adjustment of HWP1 so as to produce an elliptic polarization. Compared to the two

previous cases, the major axis of the ellipse is now standing along the vertical direction, _r_ = 1.23, with a phase _ϕ_ = 1.5 rad (−4°) that remains about constant, leading to an

ellipticity _ε_ = 0.80. The polarization shaping is also applicable for other harmonics. For instance, the result of Fig. 5(d) is obtained for the 7th harmonic with a delay of 10.45 ps. The

adjusted ellipticity and phase are _ε_ _=_ 0.74 and _ϕ_ = 1.8 rad (+13°), respectively. For technical reasons, it was not possible to measure both 7 and 9th harmonic simultaneously. The

photon flux of the highly elliptic EUV beam just after the HHG medium is ≈ 4 pJ, _i.e._, 2.106 photons/pulse. This is measured by means of an EUV calibrated photodiode in combination with

the photoelectron spectra recorded for linear and circular EUV radiation (see the Supplemental information). DISCUSSION We have shown that coherent short pulse EUV radiations with adjustable

polarization state, ranging between linear and near circular, can be produced by molecular alignment assisted high-harmonic generation. The effect demonstrated here for high-order harmonics

of low photon energies, which are suitable for probing molecular structures below their ionization thresholds, is in principle applicable to high-order harmonics of higher photon energies.

The polarization shaping is based on the difference between the field vector components of the generated harmonic, whose relative amplitudes are ruled by the angular distribution of the

molecules at the time they interact with a circularly-polarized driving field. Changing the delay between the aligning and driving pulse enables to modify to a large extent the amplitude

ratio between the two field projections. In addition, the ability to generate circular polarization requires that the two electric field components are produced in phase quadrature. This

condition is fulfilled in the case of third-harmonic generation where it has been shown experimentally and theoretically (in the framework of perturbation theory) that the transverse dipole

components oscillate in phase quadrature18. One might question whether this also applies to higher-order harmonics. Hereby it is revealed that the high-harmonic field components are in fact

produced with the proper phase relation up to the 9th harmonic. It should be noticed that a small rotation of the polarization of the harmonics was reported for atoms driven by polarized

light of moderate ellipticity (0 < _ε_ _<_ 0.4)21. In the present work, where the ellipticity of the driving field is one (or close to one) the amplitude of the two electric components

of the fundamental field are comparable. Therefore, any dephasing occurring between the generated harmonic components, leading to a rotation of the harmonic field ellipse, would most

probably result from the anisotropy of the potential of the aligned molecules rather than from the different amplitude of the two driving field components21. The harmonics generated with

large ellipticity are about two-order of magnitude less intense than the same produced with a linear polarization (see Supplementary Fig. S1). This is well understood within the so-called

three-step model22,23 interpreting high-order harmonic generation within a semiclassical approach; compared with a linear polarization, an electron accelerated in an elliptically-polarized

field has less chance to be driven back to its parent ion and thus to undergo an inelastic recollision converting its kinetic energy into the emission of a EUV photon. In systems with

central symmetry, like atoms, the three-step model prohibits any harmonic generation from circularly-polarized light in agreement with the conservation of the angular momentum. In laser

aligned molecules, the process is allowed24,25 thanks to the anisotropy of the potential. Likewise, the conservation of the angular momentum is fulfilled when considering the total external

field applied to the molecule. This last point can be evidenced by describing the harmonic generation process as a multiphoton process. A photon carries a spin angular moment that is +_ħ_ or

−_ħ_, depending if the circular polarization of the field is left- (_σ_+) or right-handed (_σ−_), respectively. Figure 6 illustrates the generation of the 9th harmonic by aligned molecules

driven by left-handed fundamental photons. The quantification axis is chosen along the propagation direction of the fields, _i.e._, perpendicular to the aligning and driving fields. In the

absence of aligning field the molecules are randomly oriented. The absorption of 9 photons, each transition obeying to the selection rule Δ_J_ = ±1, Δ_m_ = +1, leads the system to a virtual

state (_J_′, _m_ + 9) that can not be coupled to the initial state through a single-photon emission, as shown in Fig. 6(a). In this case, the HHG process is forbidden. The action of the

aligning pulse is to excite the molecule, by means of intrapulse nonresonant Raman transitions (Δ_J_ = 0, ±2, Δ_m_ = 0, ±2), to a rotational state (_J_′, _m_ − 8), with |_m_ − 8|≤_J_′26, as

shown in Fig. 6(b). Once the molecule is prepared in this state, it can be driven by the fundamental pulse through a nine-photon transition to a virtual state (_J_″, _m_ + 1) from which a

harmonic photon of same polarization as the fundamental can be emitted, bringing back the system to its initial state. The angular momentum of the “molecule + field” is thus conserved, but

with the expense that the 9th harmonic is produced though a 17-photon process involving 8 and 9 photons from the aligning and fundamental field, respectively. Within this multiphoton

picture, the difference of EUV yield between the harmonics driven by a linear polarization and those driven by a circular polarization is attributed to the increase of the nonlinearity of

the conversion process. It should be pointed out that harmonics generated by circularly-polarized light in aligned molecules should experience a spectral splitting due to the energy

conservation. This can be explained from Fig. 6(b,c). In Fig. 6(b), the energy of the 9th harmonic photon differs from the expected value, which is nine times the energy of the fundamental

photon. This shift can be interpreted as a manifestation of the rotational Doppler effect observed recently in molecular rotors probed through linear27,28,29,30 and nonlinear31 optical

interactions. A closer inspection to the quantum state excited by the aligning pulse in Fig. 6(b) reveals that the 9th harmonic is generated by molecules rotating in the opposite sense to

the driving field, giving rise to a frequency upshift of the generated radiation. In the same time, the aligning pulse also produce counter-rotating molecules relative to the circular

polarization of the fundamental field. As shown in Fig. 6(c), those molecules generate downshifted harmonics. Because the linearly-polarized aligning pulse can not orient the angular

momentum of the molecule, no preferential sense of molecular rotation is favoured and both of the scenarios depicted in Fig. 6(b,c) apply with the same probability. The generated harmonics

should be therefore spectrally split in two components. Unfortunately, the resolution of the EUV spectrometer employed in this experiment did not enable to resolve the splitting of the 7th

and 9th harmonic estimated between 6 and 8 THz for the present conditions. Compared to other existing techniques the present method, utilizing two external control parameters, namely the

delay between the two pulses and the ellipticity (close to unity) of the driving EUV field, offers significant control over the polarization of the high-order harmonics generated by a

nonresonant single-color driving laser. In contrast to methods relying on the synchronisation of polarized femtosecond driving pulses12,13,14,15,17, the polarization control mechanism

investigated here does not require a stabilization of the relative phase between the two laser (aligning and driving) pulses with interferometric accuracy. It is also applicable to all the

existing methods of producing isolated attosecond pulses with few or many cycle driving pulses and thus it can supply circularly polarized isolated pulses from the central part (highest

intensity) of the driving laser pulse, assuming that the spectral components of the EUV continuum are generated with essentially the same ellipticity. While the question regarding the

ellipticity variation in subsequent harmonics seeks for further experimental investigations, the ellipticity control of individual harmonics demonstrated here is important for applications

in itself. Compared with recent techniques employing counter-rotating circularly-polarized femtosecond laser pulses reporting similar efficiency with standard HHG process12,13,14, the

moderate efficiency of the present method limits its application to high peak power lasers. The polarization of the EUV light produced by HHG in molecules depends on the structure of the

molecular orbitals, the electronic dynamics in the ion, and the orientation of the molecule with respect to the field32. It will be fruitfull to interpret our data at the light of existing

theoretical models. This would allow, in one one hand, to assess the impact of circularly or quasi-circularly polarized light on the HHG dynamics of aligned molecules24,25 and, on the other

hand, to extract generic molecular features by decrypting the information encoded in the emitted EUV radiation through a complete analysis of its polarization state33. ADDITIONAL INFORMATION

HOW TO CITE THIS ARTICLE: Skantzakis, E. _et al_. Polarization shaping of high-order harmonics in laser-aligned molecules. _Sci. Rep._ 6, 39295; doi: 10.1038/srep39295 (2016).

PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES * McPherson, A. et al. Studies of

multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 4, 595–601 (1987). Article  CAS  ADS  Google Scholar  * Ferray, M. et al. Multiple-harmonic

conversion of 1064 nm radiation in rare gases. J. Phys. B 21, L31 (1988). Article  CAS  Google Scholar  * Brabec, T. & Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear

optics. Rev. Mod. Phys. 72, 545–591 (2000). Article  CAS  ADS  Google Scholar  * Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009). Article  ADS  Google

Scholar  * Husakou, A., Kelkensberg, F., Herrmann, J. & Vrakking, M. J. J. Polarization gating and circularly-polarized high harmonic generation using plasmonic enhancement in metal

nanostructures. Opt. Express 19, 25346–25354 (2011). Article  CAS  ADS  Google Scholar  * Yuan, K.-J. & Bandrauk, A. D. Circularly polarized molecular high-order harmonic generation in

H2+ with intense laser pulses and static fields. Phys. Rev. A 83, 063422 (2011). Article  ADS  Google Scholar  * Milošević, D. B., Becker, W. & Kopold, R. Generation of circularly

polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 61, 063403 (2000). Article  ADS  Google Scholar  * Tong, X.-M. & Chu, S.-I. Generation of circularly

polarized multiple high-order harmonic emission from two-color crossed laser beams. Phys. Rev. A 58, R2656–R2659 (1998). Article  CAS  ADS  Google Scholar  * Vodungbo, B. et al. Polarization

control of high order harmonics in the euv photon energy range. Opt. Express 19, 4346–4356 (2011). Article  CAS  ADS  Google Scholar  * Zhou, X. et al. Elliptically polarized high-order

harmonic emission from molecules in linearly polarized laser fields. Phys. Rev. Lett. 102, 073902–4 (2009). Article  ADS  Google Scholar  * Mairesse, Y. et al. High harmonic spectroscopy of

multichannel dynamics in strong-field ionization. Phys. Rev. Lett. 104, 213601 (2010). Article  CAS  ADS  Google Scholar  * Fleischer, A., Kfir, O., Diskin, T., Sidorenko, P. & Cohen, O.

Spin angular momentum and tunable polarization in high-harmonic generation. Nature Photon. 8, 543–549 (2014). Article  CAS  ADS  Google Scholar  * Kfir, O. et al. Generation of bright

phase-matched circularly-polarized extreme ultraviolet high harmonics. Nature Photon. 9, 99–105 (2015). Article  CAS  ADS  Google Scholar  * Hickstein, D. D. et al. Non-collinear generation

of angularly isolated circularly polarized high harmonics. Nature Photon. 9, 743–750 (2015). Article  CAS  ADS  Google Scholar  * Hernández-Garca, C. et al. Schemes for generation of

isolated attosecond pulses of pure circular polarization. Phys. Rev. A 93, 043855 (2016). Article  ADS  Google Scholar  * Ferré, A. et al. A table-top ultrashort light source in the extreme

ultraviolet for circular dichroism experiments. Nature Photon. 9, 93–98 (2015). Article  ADS  Google Scholar  * Lambert, G. et al. Towards enabling femtosecond helicity-dependent

spectroscopy with high-harmonic sources. Nat. Commun. 6, 1–6 (2015). Google Scholar  * Houzet, J., Hertz, E., Billard, F., Lavorel, B. & Faucher, O. Molecular alignment allows low-order

harmonic generation by circular light in a gas. Phys. Rev. A 88, 023859 (2013). Article  ADS  Google Scholar  * Ohshima, Y. & Hasegawa, H. Coherent rotational excitation by intense

nonresonant laser fields. Int. Rev. Phys. Chem. 29, 619–663 (2010). Article  CAS  Google Scholar  * Fleischer, S., Khodorkovsky, Y., Gershnabel, E., Prior, Y. & Averbukh, I. S. Molecular

alignment induced by ultrashort laser pulses and its impact on molecular motion. Isr. J. Chem. 52, 414–437 (2012). Article  CAS  Google Scholar  * Antoine, P., Carré, B., L’Huillier, A.

& Lewenstein, M. Polarization of high-order harmonics. Phys. Rev. A 55, 1314–1324 (1997). Article  CAS  ADS  Google Scholar  * Schafer, K. J., Yang, B., DiMauro, L. F. & Kulander, K.

C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 70, 1599–1602 (1993). Article  CAS  ADS  Google Scholar  * Corkum, P. B. Plasma perspective on strong-field

multiphoton ionization. Phys. Rev. Lett. 71, 1994–7 (1993). Article  CAS  ADS  Google Scholar  * Baer, R., Neuhauser, D., Zdanska, P. R. & Moiseyev, N. Ionization and high-order harmonic

generation in aligned benzene by a short intense circularly polarized laser pulse. Phys. Rev. A 68, 043406 (2003). Article  ADS  Google Scholar  * Zdanska, P., Averbukh, V. & Moiseyev,

N. High harmonic generation spectra of aligned benzene in circular polarized laser field. J. Chem. Phys. 118, 8726–8738 (2003). Article  CAS  ADS  Google Scholar  * Zare, R. N. Angular

Momentum: Understanding spatial aspects in chemistry and physics. (Wiley-Interscience, New York, 1988). * Korech, O., Steinitz, U., Gordon, R. J., Averbukh, I. S. & Prior, Y. Observing

molecular spinning via the rotational doppler effect. _Nat Photon_. 7, 711–714 (2013). * Korobenko, A., Milner, A. A. & Milner, V. Direct observation, study, and control of molecular

superrotors. Phys. Rev. Lett. 112, 113004 (2014). Article  ADS  Google Scholar  * Karras, G. et al. Polarization shaping for unidirectional rotational motion of molecules. Phys. Rev. Lett.

114, 103001 (2015). Article  CAS  ADS  Google Scholar  * Mizuse, K., Kitano, K., Hasegawa, H. & Ohshima, Y. Quantum unidirectional rotation directly imaged with molecules. Sci. Adv. 1

(2015). * Faucher, O. et al. Rotational doppler effect in harmonic generation from spinning molecules. Phys. Rev. A 94, 051402(R) (2016). Article  ADS  Google Scholar  * Smirnova, O. et al.

Attosecond circular dichroism spectroscopy of polyatomic molecules. Phys. Rev. Lett. 102, 063601–4 (2009). Article  ADS  Google Scholar  * Veyrinas, K. et al. Molecular frame photoemission:

a sensitive probe of the complete polarization state of high harmonic generation. J. Phys. B 635, 112140 (2015). Google Scholar  Download references ACKNOWLEDGEMENTS The research leading to

these results has received funding from LASERLAB-EUROPE (grant agreement no. 284464, EC’s Seventh Framework Programme) and has been further supported in part by the European Union’s Horizon

2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 641789 MEDEA, the Greek funding program NSRF, and the Labex ACTION program (contract

ANR-11-LABX-0001-01). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Foundation for Research and Technology-Hellas, Institute of Electronic Structure and Laser, P.O. Box 1527, Heraklion,

GR-711 10, Crete, Greece E. Skantzakis, S. Chatziathanasiou, D. Gray, P. Tzallas & D. Charalambidis * Department of Physics, University of Crete, P.O. Box 2208, Heraklion, GR71003,

Crete, Greece S. Chatziathanasiou & D. Charalambidis * ELI-ALPS, ELI-Hu Kft., Dugonics tér 13, Szeged, H-6720, Hungary G. Sansone, A. Nayak, P. Tzallas, D. Charalambidis & O. Faucher

* Institute of Photonics and Nanotechnologies (IFN)-Consiglio Nazionale delle Ricerche (CNR), Piazza Leonardo da Vinci 32, Milano, 20133, Italy G. Sansone * Dipartimento di Fisica

Politecnico, Piazza Leonardo da Vinci 32, Milano, 20133, Italy P. A. Carpeggiani & G. Sansone * Laboratoire Interdisciplinaire CARNOT de Bourgogne, UMR 6303 CNRS-Université Bourgogne

Franche-Comté, 9 Av. A. Savary, DIJON, BP 47870, F-21078, Cedex, France E. Hertz & O. Faucher Authors * E. Skantzakis View author publications You can also search for this author

inPubMed Google Scholar * S. Chatziathanasiou View author publications You can also search for this author inPubMed Google Scholar * P. A. Carpeggiani View author publications You can also

search for this author inPubMed Google Scholar * G. Sansone View author publications You can also search for this author inPubMed Google Scholar * A. Nayak View author publications You can

also search for this author inPubMed Google Scholar * D. Gray View author publications You can also search for this author inPubMed Google Scholar * P. Tzallas View author publications You

can also search for this author inPubMed Google Scholar * D. Charalambidis View author publications You can also search for this author inPubMed Google Scholar * E. Hertz View author

publications You can also search for this author inPubMed Google Scholar * O. Faucher View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.C.,

G.S. and O.F. initiated the project. E.S. and P.T. designed the experiment., E.S., S.C., P.A.C., A.N., E.H. and O.F. conducted the experiments. D.G. operated the laser system. P.T., D.C.,

E.H. and O.F. supervised the project, and O.F. wrote the manuscript. E.S., G.S., P.T., D.C., E.H. and O.F. analyzed the results and contributed to the manuscript. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing financial interests. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS This work is licensed under a

Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To

view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Skantzakis, E., Chatziathanasiou, S.,

Carpeggiani, P. _et al._ Polarization shaping of high-order harmonics in laser-aligned molecules. _Sci Rep_ 6, 39295 (2016). https://doi.org/10.1038/srep39295 Download citation * Received:

12 October 2016 * Accepted: 21 November 2016 * Published: 20 December 2016 * DOI: https://doi.org/10.1038/srep39295 SHARE THIS ARTICLE Anyone you share the following link with will be able

to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative