Quantum state transmission in a superconducting charge qubit-atom hybrid

Select a language for the TTS:
UK English Female
UK English Male
US English Female
US English Male
Australian Female
Australian Male
Language selected: (auto detect) - EN

Play all audios:

ABSTRACT Hybrids consisting of macroscopic superconducting circuits and microscopic components, such as atoms and spins, have the potential of transmitting an arbitrary state between

different quantum species, leading to the prospective of high-speed operation and long-time storage of quantum information. Here we propose a novel hybrid structure, where a neutral-atom

qubit directly interfaces with a superconducting charge qubit, to implement the qubit-state transmission. The highly-excited Rydberg atom located inside the gate capacitor strongly affects

the behavior of Cooper pairs in the box while the atom in the ground state hardly interferes with the superconducting device. In addition, the DC Stark shift of the atomic states

significantly depends on the charge-qubit states. By means of the standard spectroscopic techniques and sweeping the gate voltage bias, we show how to transfer an arbitrary quantum state

from the superconducting device to the atom and vice versa. SIMILAR CONTENT BEING VIEWED BY OTHERS CHARGE-4E SUPERCURRENT IN A TWO-DIMENSIONAL INAS-AL SUPERCONDUCTOR-SEMICONDUCTOR

HETEROSTRUCTURE Article Open access 22 January 2024 DIRECT MANIPULATION OF A SUPERCONDUCTING SPIN QUBIT STRONGLY COUPLED TO A TRANSMON QUBIT Article 22 May 2023 UNIMON QUBIT Article Open

access 12 November 2022 INTRODUCTION A quantum computer makes direct use of qubits to encode information and perform operations on data according to the laws of quantum mechanics1. Due to

the properties of superposition and entanglement of quantum states, such a computing device is expected to operate exponentially faster than a classical computer for certain problems.

Recently, some basic quantum logic gates have been executed on various quantum systems composed of a small number of qubits, for instances, trapped ions2, neutral atoms3, photons4, NMR5, and

superconducting (SC) circuits6. However, the development of an actual quantum computer is still in its infancy since no quantum system practically fulfills all DiVincenzo criteria7 for the

physical implementation of quantum computation. Hybridizing different quantum systems could inherit the advantages of each component and compensate the weaknesses with each other8,9,10. A

promising structure is to combine the SC circuits with neutral atoms. Macroscopic solid-state devices including submicrometer-sized Josephson junctions (JJ) possess the advantages of rapid

information processing (~1 ns), flexibility, and scalability. However, due to the strong coupling to the local electromagnetic environment, the relaxation and dephasing times of the SC

circuits, which are of the order of 10 ns~100 _μ_s11,12,13,14,15, are significantly limited by the 1/_f_ fluctuations in background charge, flux, and critical current16 and even the readout

back-action17. In contrast, the microscopic atomic systems are characterized by precise quantum-state control and long coherence time (1 ms~1 s), though they own a relatively long gate

operation time because of the weak coupling to external fields18,19,20,21 and have limited scalability. Transmitting information between these two distinct quantum realizations could lead to

the rapid processing and long-term storage of quantum states, where the SC circuits serve as the fast processor while the atoms play the role of memory22,23,24. The SC circuits and atoms

can be indirectly coupled by integrating both of them on a microwave SC cavity, such as a LC resonator or a coplanar waveguide (CPW) resonator, which acts as a data bus to transfer the

quantum information between the atomic memory and the SC processor25,26,27,28. However, the large detunings of the off-resonance SC qubit-resonator and atom-resonator interactions

significantly weaken the virtual-photon-mediated SC qubit-atom coupling. Moreover, the fluctuation of intraresonator photon number increases the dephasing rate of qubits15. The atoms can

also directly talk to the SC devices via interacting with the local electromagnetic field. The current relevant research mainly focuses on the information transmission between neutral atoms

and flux qubits, where the low-lying atomic states couple to the microwave-frequency alternating magnetic field from SC loops29,30. Although replacing a single atom by an ensemble of _N_

atoms can enhance the magnetic intersubsystem coupling by a factor of , the atomic number fluctuation and the interparticle interaction challenge the experimental implementation. These

issues may be solved by employing the electric dipole interface between the highly-excited Rydberg atomic states and local electric field from SC devices31. Here, we propose a hybrid scheme,

where a charge qubit is electrically coupled to an atomic qubit comprised of the ground and Rydberg states. The neutral atom placed inside the gate capacitor acts as the dielectric medium

and affects the gate capacitance, resulting in the modulated charge-qubit energy bands. In addition, the local quasi-static electric field strongly depends on the charge-qubit state, leading

to different DC Stark shifts of atomic-qubit states. We show that an arbitrary quantum state can be transmitted between these two distinct qubits. The two-qubit controlled-NOT (CNOT) logic

gate and single-qubit Hadamard transform, which are necessary to entangle two qubits with different species and induce a _π_-rotation of the control qubit, respectively, in the

state-transmission protocol, can be implemented by means of standard spectroscopic techniques and sweeping the gate charge bias. Our state-transmission protocol also provides a potential for

transferring the quantum state between or remotely entangling two distant noninteracting SC qubits via the flying-qubit-linked atoms. RESULTS CHARGE QUBIT-ATOM HYBRID We consider a simple

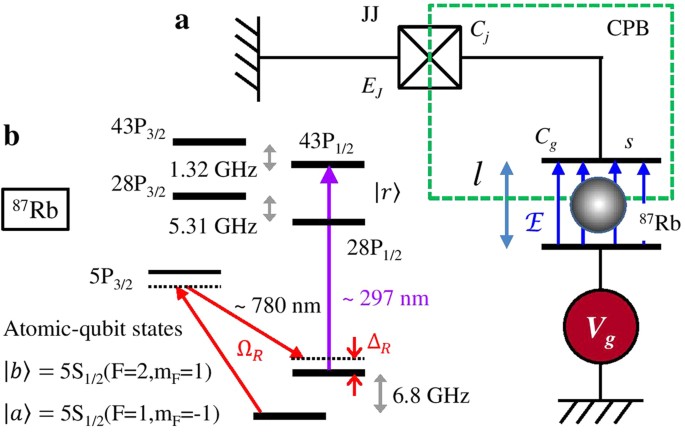
SC charge qubit32,33,34, where a single Cooper pair box (CPB) is connected to a SC reservoir via a JJ with a low self-capacitance _C__j_ (see Fig. 1a). The Cooper pairs can tunnel into or

out of the box at a rate of (the magnetic flux quantum Φ0 and the critical current _I__c_ of JJ). The CPB is biased by a voltage source _V__g_ via a parallel-plate capacitor _C__g_ with the

plate area _s_ and the interplate separation _l_. The Hamiltonian describing the dynamics of excess Cooper pairs in the box is written as where gives the Coulomb charging energy, is the

offset charge, and _δ_ is the phase drop across the JJ. The operator _N_ counts the number of excess Cooper pairs in the box, . Around the charge-degenerate spot (_N__g_ = 0.5), two lowest

charge states and are well separated from others and implement the charge qubit. We have omitted the work done by the gate voltage, whose effect on the system can be neglected. A 87Rb atom

placed inside the gate capacitor _C__g_ interacts with the internal electric field and plays a role of dielectric medium. The direction of is chosen as the the quantization axis. Two

hyperfine ground states |_a_〉 = 5_S_1/2(_F_ = 1, _m__F_ = −1) and |_b_〉 = 5_S_1/2(_F_ = 2, _m__F_ = 1) with an energy spacing of 6.8 GHz are applied to form an atomic qubit (see Fig. 1b),

where _F_ is the total angular momentum quantum number and _m__F_ gives the corresponding projection along the _z_-axis. The qubit-state flipping of the atom is achieved by the resonant

Raman transition via the intermediate 5_P_3/2 state. A highly-excited Rydberg state |_r_〉 = _nP_1/2 is employed as an auxiliary state to enhance the charge qubit-atom interaction. In

comparison with _E__J_ and _E__C_, the hyperfine splitting of |_r_〉, which is of the order of several MHz35, can be neglected. Here _n_ denotes the principle quantum number of Rydberg atom.

A resonant _π_-laser pulse at 297 nm transfers the atomic component in |_a_〉 or |_b_〉 completely to |_r_〉. The Cooper-pair tunneling through the JJ varies the internal electric field with a

frequency typically of the order of _E__J_/_ħ_ (the reduced Planck’s constant _ħ_). The energy spacings of any electric-dipole transitions associated with |_r_〉 are much larger than _E__J_.

Thus, can be treated as quasi-static. In the weak-field limit, the capacitance _C__g_ with the atom in |_u_ = _a_, _b_, _r_〉 is expressed as , where gives the empty gate capacitance (without

the atom), _ϵ_0 is the vacuum permittivity, _α__u_ denotes the static polarizability of the atom in |_u_〉, and _V_ = _sl_ is the volume of homogeneous atomic distribution over the gate

capacitor. According to , the Coulomb energy _E__C_, the offset charge _N__g_, and the internal electric field are rewritten as , , and _u_ = 036, respectively, where the empty charging

energy , the empty gate charge bias , , and the field amplitude 0 . The ratio measures the relative variation of the total box capacitance caused by the single atom. A large _η__u_ reduces

but enhances . Combining the energy associated with the atom, the system Hamiltonian is given by where denotes the SC-circuit Hamiltonian _H__c_ with the atom in |_u_〉, _ħω__u_ is the

intrinsic atomic energy of |_u_〉, indicates the DC Stark shift of |_u_〉 induced by the electric field _u_, and _P__u_ = |_u_〉〈_u_| is the atomic projection operator. We restrict ourselves

strong interface between SC circuit and atom. Diagonalizing _H_ gives us the eigenvalues and eigenstates of the hybrid system, with _k_ = 0, 1 denoting the different energy bands for a

given |_u_〉. For the zero gate voltage _V__g_ = 0, we have _N__g_0 = _N__j_ = 0 and the hybrid-system eigenenergies are analytically derived as and the corresponding eigenstates are given by

In the limit of , we are left with , , , and . For the atom in the hyperfine ground states |_u_ = _a_, _b_〉, whose static polarizabilities _α__u_ = 0.079 Hz/(V/cm)2 37 are extremely small,

we obtain , , , and , meaning the atom hardly affects the SC circuit. Thus, the energy difference between |_r_, 0〉 and |_a_, 0〉 approximates to the intrinsic energy spacing _ħω__ra_ =

_ħω__r_ − _ħω__a_, i.e., , while the energy separation between |_r_, 1〉 and |_a_, 1〉 is shifted away from _ħω__ra_, i.e., . Similarly, we have and . Distinguishing the system energy spectrum

with the atom in |_r_〉 from that associated with |_u_ = _a_, _b_〉, a large _η__r_ is necessary to induce the apparent variations of and compared with the small Josephson energy _E__J_ and

the ratio _E__J_/_E__C_0, respectively, as well as a strong DC Stark shift Δ_E__r_. Thus, the SC circuit should be carefully designed and the Rydberg |_r_〉 state needs to be chosen

accordingly. As a specification, we list the structure of CPB in Table 1. When a Rydberg atom is brought into the vicinity of SC circuit, the inhomogeneous stray electric fields originating

from the contaminations on the cryogenic surface are particular detrimental to the quantum hybrid system since they cause the unwanted energy-level shifts and destroy the atomic coherence.

However, there might be ways to mitigate or circumvent the effects of stray electric fields. It has been shown that the direction of electric field produced by the adsorbates due to the

chemisorption or physisorption depends on the material properties38. In principle, one can envision to pattern the surfaces with two materials which give rise to opposing dipole moments of

adsorbates. Furthermore, as experimentally demonstrated in ref. 39, the stray fields can be minimized by saturating the adsorbates film. The remaining uniform electric fields could be

canceled by applying offset fields. The extra measures of reducing the effects of stray fields possibly affect the performance of hybrid system in a different manner. One way to estimate the

dependence of the coherence time of a qubit on the surface properties is to investigate the surface-dependent change of the _Q_-factor of a cavity. Only a few studies have been done so far

investigating the superconducting cavity for various materials absorbed to the surface40. With the knowledge at hand, it is hard to estimate the effect of a physisorbed layer of rubidium or

specific protective coatings on the superconducting system. Here we assume the resulting decoherence time of the atomic qubit close to the surface is much longer than that of the charge

qubit. In the following, we discuss the quantum-state transfer between two different qubits. STATE TRANSMISSION FROM ATOM TO SC CIRCUIT Transferring an arbitrary qubit state from the atom to

the charge qubit primarily relies on a two-qubit CNOT logic gate, where the state flipping of the charge qubit is conditioned on the atomic-qubit state, and a one-qubit Hadamard gate acting

on the atom1. For performing the CNOT operation, the polarizability _α__r_ of Rydberg |_r_〉 state should be large enough that the atom is strongly coupled with the SC circuit. In addition,

the corresponding internal electric field _r_ needs to be smaller than the first avoided crossing field of |_r_〉41. Based on the specification of CPB structure listed in Table 1, we choose

|_r_〉 = 43_P_1/2, whose relevant physical parameters are derived from refs 42, 43, 44 and also shown in Table 1. We first consider the system energy spectrum. Figure 2a illustrates the

shifted eigenenergies with _u_ = _a_, _b_, _r_ versus the empty charge bias _N__g_0 around _N__g_0 = 0.5. For _u_ = _a_ and _b_, are nearly same to that of a common charge qubit due to . An

avoided energy-level crossing occurs at _N__g_0 = 0.5, where and approach each other with a minimal energy spacing of _E__J_. The Cooper-pair tunneling takes effect only around the

charge-degenerate point _N__g_0 = 0.5 within a narrow region |_N__g_0 − 0.5| < _E__J_/_E__C_045. In contrast, the energy bands move down relative to with _u_ = _a_, _b_ due to the

enhanced and large DC Stark shift Δ_E__r_. The minimal separation between and , however, is still determined by the Josephson energy _E__J_. The position of the corresponding energy-level

anticrossing shifts to the left side of _N__g_0 = 0.5 because of the enlarged offset charge . At either avoided crossing, the hybrid system stays in the superposition states and with . We

also show the expectation values of excess Cooper-pair numbers, , in Fig. 2b and find that two charge-degenerate spots are separated by Δ_N__g_0 = 0.016 larger than the ratio _E__J_/_E__C_0

= 0.004, indicating the shifted energy spectra with the atom in |_u_ = _a_, _b_〉 and |_r_〉 can be well distinguished. The dependence of the avoided-level crossing on the atomic state allows

us to control the charge-qubit transition via preparing the atom in different states. Setting the empty charge bias at _N__g_0 = 0.5 − Δ_N__g_0, the hybrid system resonantly oscillates

between |_r_, 0〉 and |_r_, 1〉 with a half period (_π_-pulse duration) of while the |_u_, 0〉 − |_u_, 1〉 transitions with _u_ = _a_, _b_ are strongly suppressed due to the large detuning as

shown in Fig. 2c, where the master equation involving the relaxation and dephasing of charge qubit46 is employed. It is seen that the probability of the system switching between |_r_, 0〉 and

|_r_, 1〉 reaches 0.93 at . The two-qubit CNOT gate, where the atom acts as the control qubit while the charge qubit plays the target role, can be implemented via three steps: (1) Initially,

the gate voltage stays at zero, _V__g_ = _N__g_0 = 0. Two _π_-light pulses (the time duration ) at 297 nm are applied resonantly on the |_b_, 0〉 − |_r_, 0〉 and |_b_, 1〉 − |_r_, 1〉

transitions to transfer the populations in |_b_, 0〉 and |_b_, 1〉 completely to |_r_, 0〉 and |_r_, 1〉, respectively. Thus, different components and are spectroscopically discriminated (Fig.

2a). (2) The empty charge bias _N__g_0 nonadiabatically raises to the charge-degenerate point for two adiabatic energy curves associated with |_r_, 0〉 and |_r_, 1〉, i.e., _N__g_0 = (0.5 −

Δ_N__g_0). After staying at this sweet spot for the _π_-pulse duration of , _N__g_0 decreases back to zero nonadiabatically. As a result, the populations in |_r_, 0〉 and |_r_, 1〉 switches

respectively, without affecting the components of |_a_, 0〉 and |_a_, 1〉. In steps (1) and (3), the intensities of the light pulses need to be strong enough to reduce the pulse duration

shorter than the decoherence time of the charge qubit. The experimentally feasible light-pulse length can be as small as 1 ns with a corresponding effective Rabi frequency of the order of 1

GHz47. However, for such a strong atom-light interaction, the small fine-structure splitting between |_r_〉 = 43_P_1/2 and 43_P_3/2, i.e., 2_π_ × 1.32 GHz48, affects the atom transfer between

|_b_〉 and |_r_〉. To suppress the unwanted population in 43_P_3/2, the _π_-pulse length should be chosen to fit the experimental conditions. According to Fig. 2d, can be set at 1 ns, much

shorter than the decoherence time of the charge qubit, with the corresponding Rabi frequency of 2_π_ × 0.5 GHz. The resulting atom-transfer efficiency is over 0.96. Due to the large

ground-state hyperfine splitting of 2_π_ × 6.8 GHz, the light pulses hardly affect the components of |_a_, 0〉 and |_a_, 1〉. We numerically simulate the CNOT operation with different _input_

and _output_ states via applying the master equation46. The whole gate operation duration is less that 2.5 ns. The resulting register populations are depicted in Fig. 2e based on the

specification. It is seen that the quantum logic gate preserves the charge-qubit states when the atom is prepared in |_a_〉, whereas for the atom in |_b_〉 the charge-qubit state switches

between |0〉 and |1〉 with high probabilities. The standard process fidelity49,50 reaches . After performing the CNOT gate, the transmission of quantum state from the atom to SC circuit is

straightforward. We assume that the atomic qubit is initially in an arbitrary state while the charge qubit is prepared in |0〉, leading to the system state (see Fig. 2e). Passing through the

CNOT gate, the system state becomes . Then, a single-qubit Hadamard gate acts on the atom and the hybrid system arrives at . Afterwards, we measure the atomic-qubit state and obtain or

depending on the readout which triggers an extra Pauli-_Z_ (phase-flip) gate51 acting on the SC device. As a result, the final charge qubit is in and the quantum-state transmission is

accomplished. The Hadamard gate for atomic qubit can be performed via the pulsed two-photon |_a_〉 − 5_P_3/2 − |_b_〉 Raman process with a Raman detuning Δ_R_ and a Raman coupling strength

Ω_R_ (see Fig. 1b). After adiabatically eliminating the 5_P_3/2 state, one obtains an effective light-driven two-state (|_a_〉 and |_b_〉) system with the detuning Δ_R_ and the Rabi frequency

Ω_R_. Choosing Δ_R_ = Ω_R_ > 0 and the light-pulse length leads to the time evolution operator of the atom . The operator _U_(_τ__R_) maps the atomic states |_a_〉 and |_b_〉 onto and ,

respectively, achieving the Hadamard transformation. STATE TRANSMISSION FROM SC CIRCUIT TO ATOM Similarly, the protocol for transferring an arbitrary charge-qubit state to the atom relies on

a two-qubit CNOT gate, where the atom flips its state conditioned on the charge-qubit state, and a one-qubit Hadamard gate acting on the SC circuit. We first consider the CNOT operation.

The gate voltage _V__g_ is set at zero, resulting in _N__g_0 = _N__j_ = 0. A large atomic polarizability _α__r_ for |_r_〉, which leads to a strong DC Stark shift Δ_E__r_, is necessary for

spectroscopic distinguishing four |_a_, 0〉 − |_r_, 0〉, |_a_, 1〉 − |_r_, 1〉, |_b_, 0〉 − |_r_, 0〉, and |_b_, 1〉 − |_r_, 1〉 transitions. However, the single-qubit Hadamard operation on the

charge qubit, which is performed via adiabatically sweeping _N__g_0 from 0 to 0.5, requires that the charge-degenerate spots with the atom in different states approximately locate at _N__g_0

= 0.5, i.e., . Hence, _α__r_ should not be very large. As an example, we employ |_r_〉 = 28_P_1/2, whose relevant physical parameters are listed in Table 1. The corresponding _η__r_

approximates zero, indicating the very weak effect of the atom in |_r_〉 on the SC circuit, and the avoided crossing between |_r_, 0〉 and |_r_, 1〉 occurs at _N__g_0 = 0.5. Moreover, at

_N__g_0 = 0 the energy spacings of different transitions are , , , and . For our physical specification, the DC Stark shift Δ_E__r_ of |_r_〉 reaches 2_π_ × 0.2 GHz. A _π_-laser pulse

0〉 transition due to the detuning Δ_E__r_, which is applicable to the CNOT operation. The two-qubit CNOT gate, where the charge qubit plays the control role while the atom acts as the target

qubit, can be simply implemented via three steps (see Fig. 3a): (1) Two _π_-light pulses with the pulse duration are applied resonantly on the |_b_, 0〉 − |_r_, 0〉 and |_b_, 1〉 − |_r_, 1〉

transitions to transfer the atomic population in |_b_〉 completely to |_r_〉. (2) A _π_-light pulse with the pulse length is employed to resonantly couple to the |_a_, 1〉 − |_r_, 1〉

pulses with the duration are applied again to map the atomic component in |_r_〉 back onto |_b_〉. The extra phase acquired in the gate operation can be canceled by the local operations on the

atom52. The fine-structure splitting between |_r_〉 = 28_P_1/2 and 28_P_3/2 is 2_π_ × 5.31 GHz48. To suppress the influence of 28_P_3/2 on the atom transfer between |_b_〉 and |_r_〉 in steps

(1) and (3), the _π_-light pulse duration is chosen to be , much shorter than the decoherence time of the SC circuit, with the corresponding Rabi frequency of 2_π_ × 1.25 GHz (see Fig. 3b).

In step (2), the limited frequency difference between two |_a_, 0〉 − |_r_, 0〉 and |_a_, 1〉 − |_r_, 1〉 transitions extends the _π_-pulse length and, hence, the the relaxation and dephasing of

charge qubit reduces the fidelity of two-qubit logic gate as shown in Fig. 3b. We set to obtain the optimal CNOT truth table (see Fig. 3c). The total gate duration is and the resulting

process fidelity is . After performing the CNOT gate, one can transmit an arbitrary charge-qubit state to the atom via the following three steps (see Fig. 3c): (1) CNOT operation: The hybrid

system is initially prepared in at _N__g_0 = 0. After the CNOT gate, we arrive at the system state . (2) Hadamard transform: The offset charge _N__g_0 is increased to 0.5 adiabatically. Two

components |_a_, 0〉 and |_b_, 1〉 in Ψ1 follow the adiabatic energy bands and , respectively. Actually, it is unnecessary to maintain the sweep rate of _N__g_0 constantly from 0 to 0.5.

Initially, _N__g_0 adiabatically raises from 0 at a large rate. When _N__g_0 approaches to 0.5, the sweep rate decreases to a relative low value. After the local operations for canceling the

extra accumulated phases51, the system state becomes . (3) Projective measurement: We measure the excess Cooper pairs in the box. If the readout is 0, we conclude the system state ,

otherwise, . Then, the offset charge _N__g_0 is reduced back to 0 rapidly. After an extra Pauli-_Z_ operation performed on the atom52, we finally obtain the atomic-qubit state . Thus, the

quantum-state transmission is accomplished. DISCUSSION The SC circuits operate much faster than the atomic systems. Transmitting the atomic-qubit state to the SC circuit allows the rapid

quantum gate operations. Nevertheless, these solid-state devices lose the coherence on a short time scale compared with the atomic systems. Transmitting the quantum state from the SC qubits

to the atoms allows a long-time storage. To achieve this reversible state-transmission, we have proposed a hybrid structure composed of a charge qubit and an atomic qubit. Placing the atom

inside the gate capacitor results in the atomic-state-dependence energy bands of charge qubit and the charge-state-dependence DC Stark shifts of atomic-qubit states. Applying the standard

spectroscopy techniques and sweeping the gate charge bias (gate voltage) enable the quantum-state transmission between two different qubits as well as the universal two-qubit quantum gates.

As is known, the strong coupling to the local electromagnetic environment leads to the short relaxation (_T_1) and dephasing (_T_2 < _T_1) times of SC circuits. For the common charge

qubit discussed in this paper, the excess Cooper pairs in the box lose their coherence after about 10 ns12,13,14. Based on our physical specification, the state transmission can be

accomplished within the coherence time of common charge qubit. Nonetheless, the relaxation effects of charge qubit still limit the fidelity of two-qubit gate operations. In our hybrid

system, the atom locates close to the gate-capacitor plates. The inhomogeneous Stark effect from the adsorbate electric fields on the cryogenic surface imposes a severe limitation to the

coherence of Rydberg states, reducing the fidelity of state transmission38. However, the effects of stray fields might be circumvented via coating the surfaces with adsorbates39. Moreover,

measuring the distribution of stray fields above the chip surface based on Rydberg-electromagnetically-induced transparency53 provides a potential of canceling the uniform electric fields by

offset fields. We expect the resulting coherence time of Rydberg atom much longer than that of charge qubit. Our scheme for quantum state transmission in a superconducting charge qubit-atom

hybrid opens a new prospect for quantum information processing, where the macroscopic SC devices rapidly process the quantum information which can be saved in the long-term storage composed

of a microscopic atomic system. The protocols established in this paper also allow the information transfer between two distant SC qubits. After transmitting the quantum state of a SC qubit

to a local atom, the quantum information encoded in this atom can be further transferred to another remote atom via a traveling qubit (photon)54,55,56. Subsequently, the quantum state is

transmitted to another distant SC interacting with the remote atom. Moreover, transmitting the quantum states of two entangled atoms to two distant SC qubits, respectively, results in a pair

of remotely-entangled SC qubits. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Yu, D. _et al_. Quantum State Transmission in a Superconducting Charge Qubit-Atom Hybrid. _Sci. Rep._ 6,

38356; doi: 10.1038/srep38356 (2016). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES

* Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000). * Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a

large-scale ion-trap quantum computer. Nature 417, 709–711 (2002). Article ADS CAS PubMed Google Scholar * Brennen, G. K., Caves, C. M., Jessen, P. S. & Deutsch, I. H. Quantum logic

gates in optical lattices. Phys. Rev. Lett. 82, 1060–1063 (1999). Article ADS CAS Google Scholar * Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys.

79, 135–174 (2007). Article ADS CAS Google Scholar * Vandersypen, L. M. K. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature

414, 883–887 (2001). Article ADS CAS PubMed Google Scholar * Makhlin, Y., Schön, G. & Shnirman, A. Quantum-state engineering with Josephson-junction devices. Rev. Mod. Phys. 73,

357–400 (2001). Article ADS MATH Google Scholar * Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998). Article ADS CAS Google

Scholar * Xiang, Z.-L., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653 (2013).

Article ADS CAS Google Scholar * Tian, L., Rabl, P., Blatt, R. & Zoller, P. Interfacing quantum-optical and solid-state qubits. Phys. Rev. Lett. 92, 247902 (2004). Article ADS CAS

PubMed Google Scholar * Rabl, P. et al. Hybrid quantum processors: molecular ensembles as quantum memory for solid state circuits. Phys. Rev. Lett. 97, 033003 (2006). Article ADS CAS

PubMed Google Scholar * Chiorescu, I., Nakamura, Y., Harmans, C. J. P. M. & Mooij, J. E. Coherent quantum dynamics of a superconducting flux qubit. Science 299, 1869–1871 (2003).

Article ADS CAS PubMed Google Scholar * Nakamura, Y., Pashkin, Yu. A., Yamamoto, T. & Tsai, J. S. Charge echo in a Cooper-pair box. Phys. Rev. Lett. 88, 047901 (2002). Article ADS

CAS PubMed Google Scholar * Duty, T., Gunnarsson, D., Bladh, K. & Delsing, P. Coherent dynamics of a Josephson charge qubit. Phys. Rev. B 69, 140503 (2004). Article ADS CAS

Google Scholar * Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007). Article ADS CAS Google Scholar * Rigetti, C. et al. M.

Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 86, 100506 (2012). Article ADS CAS Google Scholar * Vion, D. et al. M. H. Manipulating

the quantum state of an electrical circuit. Science 296, 886–889 (2002). Article ADS CAS PubMed Google Scholar * Schreier, J. A. et al. Suppressing charge noise decoherence in

superconducting charge qubits. Phys. Rev. B 77, 180502 (2008). Article ADS CAS Google Scholar * Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration

of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995). Article ADS MathSciNet CAS PubMed MATH Google Scholar * Monroe, C. Quantum information processing with

atoms and photons. Nature 416, 238–246 (2002). Article ADS CAS PubMed Google Scholar * Isenhower, L. et al. Demonstration of a neutral atom controlled-NOT quantum gate. Phys. Rev. Lett.

104, 010503 (2010). Article ADS CAS PubMed Google Scholar * Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313–2363 (2010).

Article ADS CAS Google Scholar * Daniilidis, N. & Häffner, H. Quantum interfaces between atomic and solid-state systems. Annu. Rev. Condens. Matter Phys. 4, 83–112 (2013). Article

ADS CAS Google Scholar * Kurizkia, G. et al. Quantum technologies with hybrid systems. PNAS 112, 3866–3873 (2015). Article ADS CAS Google Scholar * Petrosyan, D. et al. Reversible

state transfer between superconducting qubits and atomic ensembles. Phys. Rev. A 79, 040304 (2009). Article ADS CAS Google Scholar * Matre, X. et al. Quantum memory with a single photon

in a cavity. Phys. Rev. Lett. 79, 769–772 (1997). Article ADS Google Scholar * Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a

cavity. Rev. Mod. Phys. 73, 565–582 (2001). Article ADS MathSciNet MATH Google Scholar * Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit

quantum electrodynamics. Nature 431, 162–167 (2004). Article ADS CAS PubMed Google Scholar * Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447

(2007). Article ADS CAS PubMed Google Scholar * Hoffman, J. E. et al. Atoms talking to SQUIDs. Rev. Mex. Fís. S 57, 1–5 (2011). CAS Google Scholar * Patton, K. R. & Fischer, U. R.

Hybrid of superconducting quantum interference device and atomic Bose-Einstein condensate: An architecture for quantum information processing. Phys. Rev. A 87, 052303 (2013). Article ADS

CAS Google Scholar * Yu, D. et al. Charge-qubitatom hybrid. Phys. Rev. A 93, 042329 (2016). Article ADS CAS Google Scholar * Nakamura, Y., Chen, C. D. & Tsai, J. S. Spectroscopy of

energy-level splitting between two macroscopic quantum states of charge coherently superposed by Josephson coupling. Phys. Rev. Lett. 79, 2328–2331 (1997). Article ADS CAS Google Scholar

* Bouchiat, V., Vion, D., Joyez, P., Esteve, D. & Devoret, M. H. Quantum coherence with a single Cooper pair. Phys. Scripta T76, 165–170 (1998). Article ADS CAS Google Scholar *

Nakamura, Y., Pashkin, Yu. A. & Tsai, J. S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 398, 786–788 (1999). Article ADS CAS Google Scholar *

Tauschinsky, A., Newell, R., van Linden van den Heuvell, H. B. & Spreeuw, R. J. C. Measurement of 87Rb Rydberg-state hyperfine splitting in a room-temperature vapor cell. Phys. Rev. A

87, 042522 (2013). Article ADS CAS Google Scholar * Pekola, J. P. & Saira, O.-P. Work, Free energy and dissipation in voltage driven single-electron transitions. J. Low Temp. Phys.

169, 70–76 (2012). Article ADS CAS Google Scholar * Miller, T. M. Atomic and Molecular Polarizabilities. In CRC Handbook of Chemistry and Physics 81st ed. (ed Lide, D. R., CRC Press,

Boca Raton, 2000). * Chan, K. S., Siercke, M., Hufnagel, C. & Dumke, R. Adsorbate Electric Fields on a Cryogenic Atom Chip. Phys. Rev. Lett. 112, 026101 (2014). Article ADS CAS PubMed

Google Scholar * Hermann-Avigliano, C. et al. Long coherence times for Rydberg qubits on a superconducting atom chip. Phys. Rev. A 90, 040502 (2014). Article ADS CAS Google Scholar *

Knobloch, J. & Padamsee, H. Reduction of the surface resistance in superconducting cavities due to gas discharge. In _Proceeding of 8th Workshop on RF Superconductivity_, SRF-981012-10

(Padua, Italy, 1998). * O’Sullivan, M. S. & Stoicheff, B. P. Scalar polarizabilities and avoided crossings of high Rydberg states in Rb. Phys. Rev. A 31, 2718–2720 (1985). Article ADS

Google Scholar * Pritchard, J. D. Cooperative Optical Non-linearity in a blockaded Rydberg Ensemble (Springer-Theses, New York, 2012). * Löw, R. et al. An experimental and theoretical guide

to strongly interacting Rydberg gases. J. Phys. B: At. Mol. Opt. Phys. 45, 113001 (2012). Article ADS CAS Google Scholar * Branden, D. B. et al. Radiative lifetime measurements of

rubidium Rydberg states. J. Phys. B: At. Mol. Opt. Phys. 43, 015002 (2010). Article ADS CAS Google Scholar * Vion, D. Course 14 Josephson quantum bits based on a cooper pair box. In

Quantum Entanglement and Information Processing: Lecture Notes of the Les Houches Summer School 2003 1st ed (eds. Esteve, D., Raimond, J.-M., & Dalibard, J., Elsevier Science, Amsterdam,

2004). * Boissonneault, M., Gambetta, J. M. & Blais, A. Dispersive regime of circuit QED: Photon-dependent qubit dephasing and relaxation rates. Phys. Rev. A 79, 013819 (2009). Article

ADS CAS Google Scholar * Huber, B. et al. GHz Rabi Flopping to Rydberg States in Hot Atomic Vapor Cells. Phys. Rev. Lett. 107, 243001 (2011). Article ADS CAS PubMed Google Scholar

* Li, W., Mourachko, I., Noel, M. W. & Gallagher, T. F. Millimeter-wave spectroscopy of cold Rb Rydberg atoms in a magneto-optical trap: Quantum defects of the _ns_, _np_, and _nd_

series. Phys. Rev. A 67, 052502 (2003). Article ADS CAS Google Scholar * Gilchrist, A., Langford, N. K. & Nielsen, M. A. Distance measures to compare real and ideal quantum

processes. Phys. Rev. A 71, 062310 (2005). Article ADS CAS Google Scholar * Bongioanni, I., Sansoni, L., Sciarrino, F., Vallone, G. & Mataloni, P. Experimental quantum process

tomography of non-trace-preserving maps. Phys. Rev. A 82, 042307 (2010). Article ADS CAS Google Scholar * Obada, A.-S. F., Hessian, H. A., Mohamed, A.-B. A. & Homid, A. H. Quantum

logic gates generated by SC-charge qubits coupled to a resonator. J. Phys. A: Math. Theor. 45, 485305 (2012). Article MathSciNet MATH Google Scholar * Jaksch, D. et al. Fast quantum

gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211 (2000). Article ADS CAS PubMed Google Scholar * Thiele, T. et al. Imaging electric fields in the vicinity of cryogenic surfaces

using Rydberg atoms. Phys. Rev. A 92, 063425 (2015). Article ADS CAS Google Scholar * Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71

(2007). Article ADS CAS PubMed Google Scholar * Hofmann, J. et al. Heralded entanglement between widely separated atoms. Science 337, 72–75 (2012). Article ADS CAS PubMed Google

Scholar * Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013). Article ADS CAS PubMed Google Scholar Download

references ACKNOWLEDGEMENTS This research is supported by the National Research Foundation Singapore under its Competitive Research Programme (CRP Award No. NRF-CRP12-2013-03) and the Centre

for Quantum Technologies, Singapore. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Centre for Quantum Technologies, National University of Singapore, 3 Science Drive 2, Singapore, 117543,

Singapore Deshui Yu, María Martínez Valado, Christoph Hufnagel, Leong Chuan Kwek, Luigi Amico & Rainer Dumke * Institute of Advanced Studies, Nanyang Technological University, 60 Nanyang

View, Singapore, 639673, Singapore Leong Chuan Kwek * National Institute of Education, Nanyang Technological University, 1 Nanyang Walk, Singapore, 637616, Singapore Leong Chuan Kwek *

MajuLab, CNRS-UNS-NUS-NTU International Joint Research Unit, 3654, UMI, Singapore Leong Chuan Kwek * CNR-MATIS-IMM & Dipartimento di Fisica e Astronomia, Universitá Catania, Via S. Soa

64, Catania, 95127, Italy Luigi Amico * INFN Laboratori Nazionali del Sud, Via Santa Sofia 62, Catania, I-95123, Italy Luigi Amico * Division of Physics and Applied Physics, Nanyang

Technological University, 21 Nanyang Link, Singapore, 637371, Singapore Rainer Dumke Authors * Deshui Yu View author publications You can also search for this author inPubMed Google Scholar

* María Martínez Valado View author publications You can also search for this author inPubMed Google Scholar * Christoph Hufnagel View author publications You can also search for this author

inPubMed Google Scholar * Leong Chuan Kwek View author publications You can also search for this author inPubMed Google Scholar * Luigi Amico View author publications You can also search

for this author inPubMed Google Scholar * Rainer Dumke View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS R.D. envisaged the concept of

physical model. D.Y. did the calculation and analysis. D.Y. and M.M.V. provided the parameters of suitable Rydberg states. C.H. contributed the experimental realizable parameters. L.C.K.,

L.A., D.Y., and R.D. contributed the conceptual approach for analyzing the presented system. All authors participated in discussions and writing of the text. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or

other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the

Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yu, D., Valado, M., Hufnagel, C. _et al._ Quantum State Transmission in a

Superconducting Charge Qubit-Atom Hybrid. _Sci Rep_ 6, 38356 (2016). https://doi.org/10.1038/srep38356 Download citation * Received: 16 April 2016 * Accepted: 09 November 2016 * Published:

06 December 2016 * DOI: https://doi.org/10.1038/srep38356 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable

link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative

Quantum state transmission in a superconducting charge qubit-atom hybrid

Play all audios:

Trending News

Latest News