The evolution of optimal resource allocation and mating systems in hermaphroditic perennial plants

ABSTRACT By incorporating the effects of inbreeding depression (ID) on both juveniles and adults survivorship, we developed a new theoretical model for hermaphroditic perennial plants. Our

model showed that the effect of the selfing rate on the evolutionarily stable strategy (ESS) reproductive allocation depends on three parameters: (1) the self-fertilized juvenile relative

survivorship (SFJRS), (2) the self-fertilized adult relative survivorship (SFARS) and (3) the growth rate of self-fertilized adult, where the SFJRS is the survivorship of self-fertilized

juveniles divided by the survivorship of outcrossed juveniles, and likewise for the SFARS. However, the ESS sex allocation decreases as the selfing rate increases. This relationship seems

independent of the SFJRS, the SFARS, and the growth rate of self-fertilized adults. Additionally, our model showed that the complete outcrossing is an ESS when the fraction of juvenile

inbreeding depression (FJID) is less than 1/2 − _τ_, where _τ_ is the self-fertilized adults mortality rate caused by ID. In contrast, the complete selfing also acts as an ESS when the FJID

is greater than 1/2 − _τ_. These results could explain the diversity of mating strategies and related resource allocations for plants. SIMILAR CONTENT BEING VIEWED BY OTHERS THE EVOLUTION

AND MAINTENANCE OF TRIOECY WITH CYTOPLASMIC MALE STERILITY Article Open access 14 October 2024 INBREEDING DEPRESSION AFFECTS THE GROWTH OF SEEDLINGS OF AN AFRICAN TIMBER SPECIES WITH A MIXED

MATING REPRODUCTIVE SYSTEM, _PERICOPSIS ELATA_ (HARMS) MEEUWEN Article Open access 01 August 2024 FITNESS CONSEQUENCES OF HYBRIDIZATION IN A PREDOMINANTLY SELFING SPECIES: INSIGHTS INTO THE

ROLE OF DOMINANCE AND EPISTATIC INCOMPATIBILITIES Article 07 August 2021 INTRODUCTION In nature, around 72% species of plants possess characteristics reminiscent of both staminate (male,

pollen-producing) and carpellate (female, ovule-producing) parts in the same plant. Hermaphroditic characteristics such as these allow for self-fertilization1,2,3. Unfortunately,

self-fertilization often causes inbreeding depression (the reduced fitness in a given population as a result of breeding of related individuals). In some cases, though, self-fertilization

may increase the seed set (i.e., increase female fitness gains) when pollen is limited (termed _reproductive assurance_)4. More importantly, self-fertilization might increase siring success

(i.e., increase male fitness gains) when pollen devoted to selfing is more likely to accomplish fertilization than pollen devoted to outcrossing (termed _automatic selection advantage_)4,5.

In these specific situations, self-fertilization can actually enhance the fitness of the individuals (female fitness gains plus male fitness gains) through either the sole increased female

fitness gains or the male fitness gains2,6. However, the mechanism that the male or female organs should receive more allocation of resources in order to gain a fitness advantages for a

given plant species is less understood. To explore the evolution of self-fertilization in perennials, Morgan _et al_.7 first presented a life-history model with both overlapping generations

and partial self-fertilization. Motivated by the observations that self-fertilization is comparatively more common in annual plants than among perennial plants8, the authors compared annual

and perennial plant species and the conditions favoring self-fertilization. However, they neglected to explore how self-fertilization modifies the allocation of resources, and a similar

oversight in other life-history models1,6. Harder _et al_.9 considered the theoretical joint effects of inbreeding depression, reproductive assurance, gamete discounting, and reproductive

compensation on the evolution of hermaphroditic mating systems, specifically those of angiosperms. However, they neglected to explore how the inbreeding depression and mating systems

modifies the allocation of resources9. For hermaphroditic plants, self-fertilization must implement some effects on the trade-off between male and female function on resource

allocation4,6,10. For example, if self-fertilization increases the fitness of organism through reproductive assurance, allocating more resources to female production could enhance the

fitness of organisms2,4,10. On the contrary, if self-fertilization increases the fitness of organism through automatic selection advantage, allocating more resources to male production could

enhance the fitness of organisms2,4,10. In either event, the fitness is increased in some way with a trade off. The increased resources in one activity must be at expense of the other.

Therefore, a given organism must decide to allocate its limited resources to either the production of male or female1,2. Zhang6 constructed a resource allocation model that analyzes how

self-fertilization influences resource allocation for partially selfing hermaphroditic plants6. This model assumed that inbreeding depression only affects the survivorship of juveniles,

which may only be true for annual plants. For perennial plants, instead, the inbreeding depression has been shown to potentially affect the survivorship of both juveniles and adults2,6,11.

If inbreeding depression affects both the survivorship of juveniles and adults, the self-fertilization will influence resource allocation. This element could then be incorporated in a new

and more generalized model. By incorporating these elements, we can explore several questions, under the assumption that inbreeding depression affects the survivorship of both juveniles and

adults, (i) how an individual adjusts resource allocation strategy according to the level of the selfing rate, and (ii) how an individual selects might then mating strategies under different

life histories. METHODS In our model, we only consider plants belonging to hermaphroditic perennial species, with discrete breeding seasons and overlapping generations. The individual of

these species usually reach reproductive maturity after a single period (such as, 1 year) and do not alter their life-history parameters, such as survivorship and fertility6,12. We further

assume that the density-dependent effect has no impact on offspring production and survival of the adult individuals. As it occurs naturally, we also assume that the resources available to

the individual are limited, and that the resources can be spent only once. Subsequently, each individual in a monomorphic population has a total of _R_ limiting resources to allocate to the

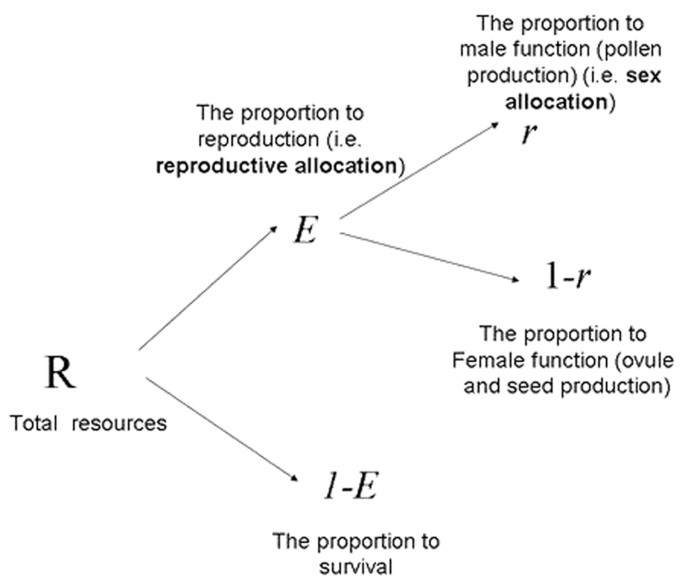
three competing functions of male production, female production, and survival. Let each individual allocate a proportion _M_ to the male function (pollen production), a proportion _F_ to the

female function (ovule and seed production) and the remaining proportion to its survival 1 − (_M_ + _F_). Thus, the total reproductive allocation (the proportion of total resources

allocated to reproduction) can be denoted by _E_ = _M_ + _F_ and the remaining proportion 1 − _E_ to survival. Sex allocation (the proportion of reproductive resources allocated to male

production) can be denoted by _r_ = _M_/_E_ and the remaining proportion of reproductive resources to female production (see Fig. 1). Since in these species inbreeding depression occurs

repeatedly during several stages of their life history6,12,13, we assume that it affects differently juvenile and adult survivorship. Therefore, let a fraction _s_ of the juveniles be

selfed, and a selfed juvenile have viability _P__j__w__j_ relative to a viability of _P__j_ for an outcrossed juvenile, where _w__j_ = 1 − _δ__j_ is the survivorship of self-fertilized

juveniles relative to outcrossed juveniles (termed _self-fertilized juvenile relative survivorship_) and _δ__j_ is the fraction of selfed juveniles inbreeding depression14. Let _P__a_ be an

outcrossed adult survivorship and _P__a__w__a_ be a self-fertilized adult survivorship, where _w__a_ = 1 − _δ__a_ is the survivorship of self-fertilized adults relative to outcrossed adults

(termed _self-fertilized adult relative survivorship_) and _δ__a_ is the fraction of self-fertilized adults inbreeding depression. Let _S_ be the fraction of self-fertilized adults. Since

the self-rate _s_ can affect the fraction (_S_), we assume that _S_ to be the function of _s_, that is _S_ = _S_(_s_). Let _P__a_ be adult survivorship, _f_ be the number of seeds produced

and _m_ be the number of pollen produced be functions of their respective resource investment, that is, _f_ = _f_(_F_), _m_ = _m_(_M_) and _P__a_ = _P__a_(_E_), and _P__j_ is a constant. The

parameters of our model are summarized in Table 1. We consider the fate of a rare mutant that allocates a proportion _M_′ of _R_ to pollen reproduction and _F_′ to ovule and seed

production. We do this following the ESS theory15 which determines whether the allocation pattern (_M_, _F_) is evolutionarily stable. We only consider a hermaphroditic perennial plant and

the mutant with a total fitness given by the sum of the female fitness of the mutant and male fitness of the mutant. The female fitness of the mutant is the sum of the number of adult as a

seed parent surviving in the next generation and the number of successful gametes as a seed parent: The first term of the right-hand side of Equation (1) is denoted by . The second term is

denoted by . Thus, the female fitness of the mutant can be written as . Similarly, the male fitness of the mutant is the sum of the number of adults as a pollen parent surviving in the next

generation and the number of successful gametes as a pollen parent: For simplicity, the first term of the right-hand side of Equation (2) is denoted by . The sum of the second term and the

third term is denoted by . Thus, the male fitness of the mutant can be written as . Notice that it is possible to have a different formulation with Equations (1) and (2), for example,

Charlesworth and Charlesworth16. Assume that _W__o_ is the total fitness gains through allocation to ovules and _W__p_ is the fitness gains through allocation to pollen16. This usage is

biologically appropriate for outcrossing species (_s_ = 0), in which and . However, in most cases, they may not equal. For the sake of consistency, it is reasonable to reserve female fitness

and male fitness for Equations (1) and (2), respectively, for the purpose of consistency. From the above analysis, the total fitness _W_ of the mutant is Let the common resource allocation

(_M_, _F_) be evolutionarily stable, therefore, _W_ is a function of with respective to _M_′ and _F_′. The total fitness _W_ must attain its maximum at (_M_′, _F_′) = (_M_, _F_), that is

From Equations (4) and (5), we can see that these necessary conditions for an interior ESS are equal to Equation (6) provides more generalized description for naturally occurring

hermaphroditic perennial species than the previous results6,17. Noted _w__a_ = 1, namely _δ__a_ = 0, which indicates no inbreeding depression in adult, which is the similar to the Zhang6.

For our purposes, we use the notation of reproductive allocation (_E_) and sex allocation (_r_). Due to the definitions of reproductive allocation and sex allocation, we obtain _M_′ = 

_E_′_r_′, _M_ = _Er_, _F_′ = _E_′(1 − _r_′) and _F _= _E_(1 − _r_). By substituting them into Equation (3) and differentiating _W_ with respective to _E_′ and _r_′, we have Note that and

Thus, Equations (7) and (8) can be rearranged as To ensure _W_ attains a maximum rather than a minimum at _M_ and _F_ (or _E_ and _r_). we also need to calculate its second derivative

conditions18. The above Equations ((4)–(5, ) or (9)–(12)) are consistent with the general conditions for an ESS. Furthermore, from Equations (4) or (9) we obtain that the ESS reproductive

allocation (_E_) will be independent of sex allocation (_r_), if and only if, female fitness gain is a linear function of resource investment (see Appendix S1). Let, where _f_max represents

the maximum number of seeds produced when all available resources is spent on seed production, then Equation (9) reduces to This suggests that the optimal reproductive allocation (_E_) does

not depend on the sex allocation (_r_) echoing a similar result for outcrossing hermaphrodites18. RESULTS ESS REPRODUCTIVE ALLOCATION Given a linear function _f_ () and a linear function _S_

(, where _γ_ is the growth rate of self-fertilized adult, and 0 < _γ_ < 1), from Equation (11), the ESS requires that It is worth noting that the effect of the selfing rate on the ESS

reproductive allocation depends on the ratio of _w__j_ to 1 − _γ_ + _γw__a_, where _w__j_ and _w__a_ is the self-fertilized juvenile relative survivorship and the self-fertilized adult

relative survivorship respectively, and _γ_ is the growth rate of self-fertilized adult. From Equation (14), our model shows that the ESS reproductive allocation increases as the selfing

rate increases when the ratio of _w__j_ to 1 − _γ_ + _γ w__a_ is greater than 1/2, whereas the reverse is true when the ratio of _w__j_ to 1 − _γ_ + _γw__a_ is less than 1/2. Particularly,

the ESS reproductive allocation will be independent on the selfing rate when the ratio of _w__j_ to 1 − _γ_ + _γw__a_ equals to 1/2 (see Appendix S2 and Fig. 2). The results we give here are

more generalized than the result of Zhang’s6. In particular, the ESS reproductive allocation (_E_) increases as _s_ increases if _δ__j_ < 1/2, which is the special case of the ratio of

_w__j_ to 1 − _γ_ + _γw__a_ being greater than 1/2 (i.e. _w__a_ = 1). Most of population genetic models in fact suggest that selfing can evolve if _δ__j_ < 1/219. ESS SEX ALLOCATION In

the following context, let _f_ be a linear function () and _m_ be a power function of the resource allocation investment. That is, , where _m_max represents the maximum number of pollens

produced when all available resources are spent on pollen production. Thus, the ESS sex allocation (_r_) can be solved as Equation (16) implies that sex allocation does not depend on the

total reproductive allocation and does not depend on the self-fertilized adult relative survivorship. Furthermore, Equation (16) shows that the sex allocation decreases as the selfing rate

increases. This relationship dose not depend on the self-fertilized juvenile relative survivorship and the self-fertilized adult relative survivorship, since . In addition, we also show that

the relationship does not depend on the specific assumption of _m_ being a power function of resource investment (see Appendix S3 and Fig. 3). Thus, sex allocation should generally decrease

with increased selfing rate, regardless of the exact forms of the male fitness function (_m_). THE SELECTION OF THE ESS MATING STRATEGIES In the preceding analysis, we took the selfing rate

as a constant, and from there we worked out the ESS reproductive allocation (_E_) and sex allocation (_r_). In what follows, we assume that the selfing rate is a variable, and considered

the evolution of selfing rate. Changes in a species’ mating strategy (changes in the selfing rate, especially) may lead to the changes in resource allocation20. Then, the corresponding

fitness for a mutant individual is Clearly, This means that a complete selfing or complete outcrossing can be evolutionarily stable, depending on the sign of . From Equation (18), when the

fraction of juvenile inbreeding depression (_δ__j_) is less than 1/2 − _τ_, we have . In other words, under this condition, the species chooses the complete outcrossing as the ESS (see Fig.

4). When the fraction of juvenile inbreeding depression (_δ__j_) is greater than 1/2 − _τ_, we have , which means the complete selfing is an ESS (see Fig. 4). The parameter is defined here

as the self-fertilized adult mortality rate caused by inbreeding depression, which is similar to the concept of _infant mortality rate_ in demography21. DISCUSSION Existed models assumed

that inbreeding depression only affects the survivorship of juveniles, and they dealt with how self-fertilization influences resource allocation2,6,7. This assumption is true for annual

plants, but may not be ture for perennial plants, because inbreeding depression may affect the survivorship of both juveniles and adults. This may lead to a allocation for optimal resource

different than custom. Simultaneously, the selection of the mating strategies may also be chosen differently. This leads to the distinct mating system found in perennial plant6,7,11.

Accordingly, the model we describe here shows that when assuming inbreeding depression has an effect on the survivorship of both juveniles and adults, the effects of the selfing rate on

reproductive allocation and the selection of mating strategy depend strongly on three parameters: (1) the self-fertilized juvenile relative survivorship, (2) the self-fertilized adult

relative survivorship and (3) the growth rate of self-fertilized adult (where the self-fertilized juvenile relative survivorship is the survivorship of self-fertilized juvenile divided by

the survivorship of outcrossed juvenile, and likewise for self-fertilized adult relative survivorship). Our model shows that fluctuations in the selfing rate that leads to the variation of

the ESS reproductive allocation is greatly affected by (1) the self-fertilized juvenile relative survivorship (its magnitude given by _w__j_ = 1 − _δ__j_), (2) the self-fertilized adult

relative survivorship (_w__a_ = 1 − _δ__a_) and (3) the growth rate of self-fertilized adults (_γ_). On the other hand, inbreeding depression on both self-fertilized juveniles (_δ__j_) and

adults (_δ__a_) is strongly affected by environmental conditions22,23. The impact of environmental conditions on juvenile inbreeding depression (_δ__j_) and adult inbreeding depression

(_δ__a_), however, may differ under different circumstances22. If the effect of the environmental condition on adult inbreeding depression is comparatively much more severe than it is on

juvenile inbreeding depression, the self-fertilized juvenile relative survivorship should accordingly be much greater than the self-fertilized adult relative survivorship (i.e. the ratio of

_w__j_ to 1 − _γ_ + _γw__a_ possibly is greater than 1/2, Fig. 2, red line). In such situation, the increase in selfing rate may raise the proportion of overall reproduction (i.e.

reproductive allocation). Conversely, if the effect of a given environmental condition on juvenile inbreeding depression is much more severe than on adult inbreeding depression, the

self-fertilized juvenile relative survivorship should be much less than the self-fertilized adult relative survivorship (i.e. the ratio of _w__j_ to 1 − _γ_ + _γw__a_ possibly is less than

1/2, Fig. 2, blue line). In this situation, the increases in selfing rate may reduce the proportion of reproductive allocation. In particular, if the self-fertilized juvenile relative

survivorship is equal to 1/2 times 1 − _γ_ + _γw__a_ (i.e. the ratio of _w__j_ to 1 − _γ_ + _γw__a_ possibly equals 1/2, Fig. 2, black line), the ESS reproductive allocation is independent

on the selfing rate. Our model also shows that the ESS sex allocation decreases as the selfing rate increases independent from the self-fertilized juvenile relative survivorship (Fig. 3).

This prediction agrees with many empirical observations made on perennial plants2,11,24,25,26. For instance, _Ranunculaceae_ plants have reduced the allocation to male function and

attractive structures such as petals that could increase the selfing rate26. Moreover, the ESS sex allocation decreases as the selfing rate increases, which does not depend on the assumption

of _m_ being a power function of resource investment (see Appendix S3). This is also in agreement with the prediction of Zhang’s6, though his model only considered the effect inbreeding

depression on self-fertilized juveniles. Inbreeding depression on both self-fertilized juveniles and self-fertilized adults is strongly affected by environmental conditions22,23. The

fraction of juvenile inbreeding depression and adults inbreeding depression may therefore be different among species or within species under different environmental conditions. In our model,

if the fraction of juvenile inbreeding depression (_δ__j_) is less than 1/2 − _τ_, (where _τ_ is the self-fertilized adult mortality rate caused by inbreeding depression), our model shows

that the complete outcrossing is an ESS mating strategy. Conversely, the complete selfing is also an ESS mating strategy. Although no studies have shown an empirical correlation between

mating strategy and the fraction of juvenile and adult inbreeding depressions, some empirical observation or experiments have implied that these inbreeding depressions can potentially affect

the resulting of mating strategy adopted by these plants6,7,25,27,28. We recall several empirical studies showing that the mating strategy adopted by annual plants is the one of complete

selfing, in the case of the juvenile inbreeding depression being less than 1/2. In our model, if the adult inbreeding depression equals to zero and the fraction of juvenile inbreeding

depression (_δ__j_) is less than 1/2 − _τ_, the juvenile inbreeding depression becomes less than 1/2. While our model derived from several basic assumptions that are comparatively simpler

than we would actually observe in nature, but it offers some interesting possibilities in both predicting and arriving at a greater understanding how the self-fertilized juvenile relative

survivorship, the self-fertilized adult relative survivorship and the growth rate of self-fertilized adult affect ESS mating strategies and resource allocation. The theoretical nature of

this model necessitates future, direct empirical demonstration of the expected correlation between mating strategy and these parameters for perennial plants. This can be facilitated by

direct molecular estimates or micro-satellites2. Following such observations, we can construct a more refined model, mirroring more closely the strategies adopted by perennial plants. This

model would consider more realistically e.g. differences in ages and life-stages, the effect of cooperation of population on resource allocation29,30,31. This further step would improve our

understanding of how perennials allocate resources depending on the countless environmental conditions they are faced with. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Wang, Y.-Q. _et

al_. The evolution of optimal resource allocation and mating systems in hermaphroditic perennial plants. _Sci. Rep._ 6, 33976; doi: 10.1038/srep33976 (2016). REFERENCES * Charnov, E. L. _The

theory of sex allocation._ (Princeton University Press, 1982). * West, S. _Sex allocation._ (Princeton University Press, 2009). * Yampolsky, C. & Yampolsky, H. _Distribution of sex

forms in the phanerogamic flora._ (Swets & Zeitlinger, 1966). * Zhang, D. Y. & Jiang, X. H. Mating system evolution, resource allocation, and genetic diversity in plants. _Acta

Phytoecologica Sinica_ 25, 130–143 (2001). Google Scholar  * Piper, J. G., Charlesworth, B. & Charlesworth, D. A high rate of self-fertilization and increased seed fertility of homostyle

primroses. _Nature_ 310, 50–51, 10.1038/310050a0 (1984). Article  ADS  Google Scholar  * Zhang, D. Y. Resource allocation and the evolution of self-fertilization in plants. _American

Naturalist_ 155, 187–199 (2000). Article  Google Scholar  * Morgan, M. T., Schoen, D. J. & Bataillon, T. M. The evolution of self-fertilization in perennials. _American Naturalist_ 150,

618–638, 10.1086/286085 (1997). Article  CAS  PubMed  Google Scholar  * Stebbins, J. C. _Variation and evolution in plants._ (Columbia University Press, 1950). * Harder, L. D., Richards, S.

A. & Routley, M. B. Effects of reproductive compensation, gamete discounting and reproductive assurance on mating-system diversity in hermaphrodites. _Evolution_ 62, 157–172 (2008).

Article  Google Scholar  * Hardy, I. _Sex ratios: concepts and research methods._ (Cambridge University Press, 2002). * Ruan, C. J., Qin, P. & Teixeira da Silva, J. A. T. Relationship

between reproductive assurance and mixed mating in perennial Kosteletzkya virginica. _S Afr J Bot_ 77, 280–291, 10.1016/j.sajb.2010.08.012 (2011). Article  Google Scholar  * Charnov, E. L.

& Schaffer, W. M. Life-History Consequences of Natural-Selection - Coles Result Revisited. _American Naturalist_ 107, 791–793, 10.1086/282877 (1973). Article  Google Scholar  * Husband,

B. C. & Schemske, D. W. Evolution of the magnitude and timing of inbreeding depression in plants. _Evolution_ 50, 54–70, 10.2307/2410780 (1996). Article  PubMed  Google Scholar  *

Charlesworth, D. & Charlesworth, B. Allocation of Resources to Male and Female Functions in Hermaphrodites. _Biol J Linn Soc_ 15, 57–74, doi: 10.1111/j.1095-8312.1981.tb00748.x (1981).

Article  MATH  Google Scholar  * Smith, J. M. & Price, G. The Logic of Animal Conflict. _Nature_ 246, 15 (1973). Article  ADS  Google Scholar  * Charlesworth, D. & Charlesworth, B.

Inbreeding Depression and Its Evolutionary Consequences. _Annu Rev Ecol Syst_ 18, 237–268, 10.1146/annurev.es.18.110187.001321 (1987). Article  Google Scholar  * Lloyd, D. G. & Venable,

D. L. Some Properties of Natural-Selection with Single and Multiple Constraints. _Theoretical population biology_ 41, 90–110, 10.1016/0040-5809(92)90051-T (1992). Article  MATH  Google

Scholar  * Zhang, D. Y. & Wang, G. Evolutionarily stable reproductive strategies in sexual organisms: an integrated approach to life-history evolution and sex allocation. _American

Naturalist_, 65–75 (1994). * Lande, R. & Schemske, D. W. The Evolution of Self-Fertilization and Inbreeding Depression in Plants.1. Genetic Models. _Evolution_ 39, 24–40, 10.2307/2408514

(1985). Article  PubMed  Google Scholar  * Holsinger, K. E. Pollination biology and the evolution of mating systems in flowering plants. _Evol Biol_ 29, 107–149 (1996). Google Scholar  *

Andrews, K., Brouillette, D. & Brouillette, R. Mortality, Infant. _Encyclopedia of Infant and Early Childhood Development_ 2, 343–358 (2008). Article  Google Scholar  * Keller, L. F.,

Grant, P. R., Grant, B. R. & Petren, K. Environmental conditions affect the magnitude of inbreeding depression in survival of Darwin’s finches. _Evolution_ 56, 1229–1239 (2002). Article

  Google Scholar  * Stevens, J. P. & Bougourd, S. M. Inbreeding Depression and the Outcrossing Rate in Natural-Populations of Allium-Schoenoprasum L (Wild Chives). _Heredity_ 60,

257–261, 10.1038/Hdy.1988.40 (1988). Article  Google Scholar  * Brunet, J. Sex Allocation in Hermaphroditic Plants. _Trends Ecol Evol_ 7, 79–84, 10.1016/0169-5347(92)90245-7 (1992). Article

  CAS  PubMed  Google Scholar  * Morgan, M. T. & Wilson, W. G. Self-fertilization and the escape from pollen limitation in variable pollination environments. _Evolution_ 59, 1143–1148

(2005). Article  Google Scholar  * Zhao, Z. G. & Du, G. Z. Characteristics of the mating system and strategies for resource allocation in Ranunculaceae. _Journal Lanzhou Unniversity

Natural Sciences_ 39, 70–74 (2003). Google Scholar  * Schemske, D. W. & Lande, R. The Evolution of Self-Fertilization and Inbreeding Depression in Plants. 2. Empirical Observations.

_Evolution_ 39, 41–52, 10.2307/2408515 (1985). Article  PubMed  Google Scholar  * Vergeer, P., Wagemaker, N. & Ouborg, N. J. Evidence for an epigenetic role in inbreeding depression.

_Biol Letters_ 8, 798–801, 10.1098/rsbl.2012.0494 (2012). Article  Google Scholar  * Chen, X., Zhang, Y., Huang, T. Z. & Perc, M. Solving the collective-risk social dilemma with risky

assets in well-mixed and structured populations. _Physical Review E_ 90, 052823–052823 (2014). Article  ADS  Google Scholar  * Wang, Z., Szolnoki, A. & Perc, M. Rewarding evolutionary

fitness with links between populations promotes cooperation. _Journal of Theoretical Biology_ 349, 50–56 (2014). Article  MathSciNet  Google Scholar  * Chen, X. & Perc, M. Optimal

distribution of incentives for public cooperation in heterogeneous interaction environments. _Operative Orthopädie Und Traumatologie_ 26, 361–368 (2014). Article  Google Scholar  Download

references ACKNOWLEDGEMENTS This research was supported by NSFC-Yunnan United fund (U1302267), the National Science Fund for Distinguished Young Scholars (31325005), the National Natural

Science Foundation of China (31600299, 31170408, 31270433, 31370408) and the key project of Baoji University of Arts and Sciences (ZK16050). We thank Shi-qian Xu, Riccardo Pansini, Derek W.

Dunn, Jun-zhou He and Lei-Gao for their discussion on the results of this manuscript. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institute of Mathematics and Information Science, Baoji

University of Arts and Sciences, Baoji, Shaanxi, China Ya-Qiang Wang * School of Mathematics and Statistics, Yunnan University, Kunming, Yunnan, China Yao-Tang Li * Center for Ecological and

Environmental Sciences, Key Laboratory for Space Bioscience & Biotechnology, Northwestern Polytechnical University, 710072, Xi’an, China Rui-Wu Wang Authors * Ya-Qiang Wang View author

publications You can also search for this author inPubMed Google Scholar * Yao-Tang Li View author publications You can also search for this author inPubMed Google Scholar * Rui-Wu Wang View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Y.-Q.W. and R.-W.W. took primary responsibility for writing the text, Y.-Q.W., R.-W.W. and

Y.-T.L. constructed the model, and Y.-Q.W., R.-W.W. and Y.-T.L. developed the ideas and discussed the interpretation of the results. All authors read and approved the final manuscript.

CORRESPONDING AUTHOR Correspondence to Rui-Wu Wang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION (PDF 135 KB) RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article

are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to

obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS

ARTICLE CITE THIS ARTICLE Wang, YQ., Li, YT. & Wang, RW. The evolution of optimal resource allocation and mating systems in hermaphroditic perennial plants. _Sci Rep_ 6, 33976 (2016).

https://doi.org/10.1038/srep33976 Download citation * Received: 03 June 2016 * Accepted: 06 September 2016 * Published: 29 September 2016 * DOI: https://doi.org/10.1038/srep33976 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative