Cascading multispectral polarization cages

ABSTRACT 3D optical polarization structures are complex structured beams and possess exotic optical properties. Multispectral information can dramatically increase information capacity. To

meet the requirement of the prevailing trend towards integration and compactness, there is an urgent need to develop ultrathin elements capable of simultaneously controlling polarization and

color in three-dimensional (3D) space. Cascading multiple 3D polarization structures with different colors has not been reported due to the fundamental challenge. We use a geometric

metasurface to generate cascaded polarization cages and dynamically modulate their polarization profiles. A red polarization cage is embedded in the second cyan polarization cage. Different

polarization cages are generated by controlling the incident wavelength, while their polarization distributions are modulated by controlling the incident linear polarization. This approach

integrates 3D polarization generation, multiple colors, and cascading technology, providing extra degrees of freedom for metasurface design and enabling small-volume polarization systems for

engineering 3D vector beams. SIMILAR CONTENT BEING VIEWED BY OTHERS COLOR-SELECTIVE THREE-DIMENSIONAL POLARIZATION STRUCTURES Article Open access 17 October 2022 METASURFACE OPTICS FOR

ON-DEMAND POLARIZATION TRANSFORMATIONS ALONG THE OPTICAL PATH Article 28 January 2021 STRUCTURING TOTAL ANGULAR MOMENTUM OF LIGHT ALONG THE PROPAGATION DIRECTION WITH POLARIZATION-CONTROLLED

META-OPTICS Article Open access 29 October 2021 INTRODUCTION Color and polarization are fundamental attributes of light, each playing a crucial role in understanding optics and

applications. 3D polarization distributions are garnering significant interest owing to their peculiar properties1,2, such as the non-orientable surfaces in Möbius strips2,3, and their

potential applications, including micro- and nanofabrication4,5, complex light beam engineering6,7, and photoalignment techniques for patterning liquid crystals8. Multi-color polarization

manipulation can introduce extra degrees of freedom. It is challenging both technically and fundamentally to cascade multiple multispectral 3D polarization structures. Moreover, fuelled by

system integration and miniaturization, there is considerable interest in developing compact optical devices capable of controlling polarization and color simultaneously along arbitrary 3D

curves. Optical metasurfaces, ultra-thin planar elements composed of nanostructures at the subwavelength scale, have emerged as a paradigm for engineering electromagnetic space and have

shown unusual capabilities of optical field manipulation in multiple dimensions9,10,11,12,13,14. Metasurface-based flat optics have revolutionized optical design, providing compact platforms

to realize ultrathin optical devices with novel functionalities. By meticulously designing the geometric parameters and arrangement of subwavelength nanostructures, various ultrathin

optical metadevices such as metalenses14,15,16,17, metasurface holograms18,19,20,21, vortex beam generators22,23, and metasurface spectrometer24,25 have been proposed. Recently, a multi-foci

metalens model was used to generate 3D polarization distributions, including different types of 3D polarization knots26,27,28,29. However, each polarization knot includes only a single

color. Generating, manipulating, and cascading multispectral 3D polarization structures can add extra degrees of freedom. Moreover, there is a growing demand for single devices that offer

multiple functionalities, especially in applications prioritizing compactness and integration. Additionally, cascading control can enhance both capacity and security in information encoding.

There is an interesting question of developing a super metalens that can simultaneously encode 3D polarization and color information into a cascaded 3D light structure. However, cascading

multiple 3D polarization structures with different colors has not been reported. To address the abovementioned challenges, we introduce a metasurface approach capable of performing such a

complex optical task. A new metalens is proposed to create cascaded polarization cages composed of six different 2-foil knots and dynamically adjust their polarization profiles. A red

polarization cage is embedded within the second cyan polarization cage, and various 3D polarization cages are obtained by altering the incident wavelength. Moreover, by adjusting the

incident linear polarization, the polarization distributions on the cascaded polarization cages can be further modulated. Cascaded polarization structures with different colors can be

utilized for optical encryption, significantly enhancing the security level and information capacity. Our approach has tackled the typical challenges of cascading multiple multispectral 3D

polarization structures: 3D polarization generation, multiple colors, and cascading control. The compact, flexible, and lightweight design of the metasurface provides numerous advantages

over traditional polarization optics, making it highly suitable for applications across various research fields, including complex vector beam generation and optical

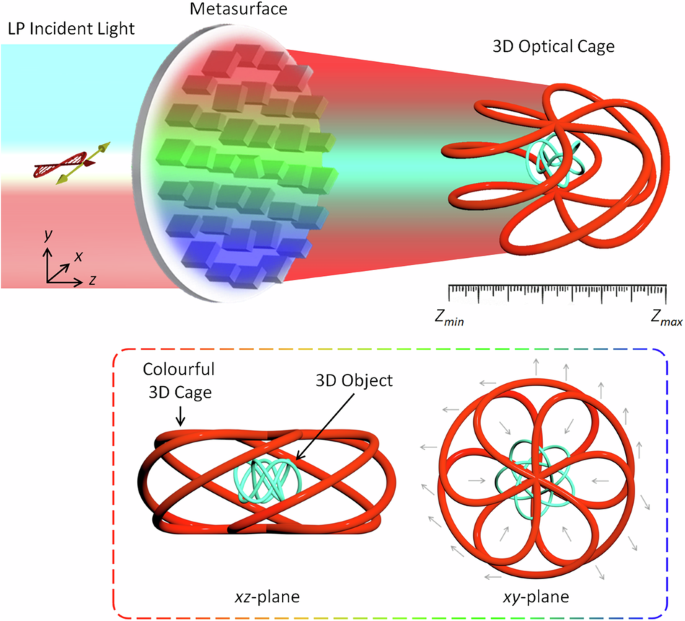
encryption6,7,30,31,32,33. RESULTS DESIGN PRINCIPLE OF CASCADED POLARIZATION CAGES Figure 1 schematically illustrates the generation of cascaded multispectral polarization cages via a

geometric metasurface consisting of nanostructures with various orientations. Under the illumination of a linearly polarized (LP) light beam with two wavelengths, a small polarization cage

and a big polarization cage with predesigned polarization and color information are created at the same observation region. For a single incident wavelength, only one polarization structure

at that wavelength is observed. By altering the incident wavelengths, various 3D polarization structures can be produced. Furthermore, the polarization distribution on the cascaded cages is

dynamically modulated by altering the incident linear polarization direction and indirectly unveiled with modulated intensity patterns after passing through a linear polarizer (analyzer).

These modulated 3D intensity patterns can be regarded as concealed 3D information and can be used for encryption applications. Various encryption information concealed within the big 3D

polarization cage can only be decoded by utilizing the correct combined keys: incident LP state, transmission axis of the analyzer, incident wavelength, and observation region, dramatically

increasing the information security and capacity. To generate the cascaded polarization cages, the geometric metasurface design consists of four parts: multiple focal points design,

polarization state control, multiple 3D polarization cage cascading, and engineered color information. We begin with a lens featuring discretized focal points along arbitrary 3D

trajectories, which are extended to continuous focal curves (such as 3D knots and digital numbers) by increasing the focal point density. Secondly, we encode the polarization state for each

focal point using the polarization rotation capability of the metalens under the illumination with incident light with LP34. Finally, the wavelength is introduced in the design to include

color information in the metalens design based on the dispersion effect, which can realize color-selective polarization cages. To generate multiple focal points along a predesigned 3D

trajectory, we first design a metalens for the _n_th focal point located on the trajectory. The corresponding phase profile is given by: $${\varphi }_{n}\left(x,y\right)=-\frac{2{\rm{\pi

}}}{\lambda }\left(\sqrt{{f}_{n}^{2}+{\left(x-{x}_{n}\right)}^{2}+{\left(y-{y}_{n}\right)}^{2}}-\sqrt{{f}_{n}^{2}+{x}_{n}^{2}+{y}_{n}^{2}}\right)$$ (1) where (_x__n__, y__n_, _f__n_)

represent the coordinates of the _n_th focal point in 3D space. _λ_ and _f__n_ are the working wavelength and the focal length, respectively. The desired phase profile _Φ_(_x_, _y_) for

multiple discretized focal points is governed by $$\varPhi \left(x,\,y\right)={\rm{\arg }}\left\{\mathop{\sum }\limits_{n=1}^{N}{(e}^{i[{\varphi }_{n}\left(x,y\right)]})\right\}$$ (2) where

_N_ represents the total number of focal points. By increasing the value of _N_, a continuous focal curve can be obtained. To realize this metalens with multiple focal points, a geometric

metasurface composed of gold nanorods with various orientation angles _θ_ is used to produce a Pancharatnam-Berry phase profile associated with left circularly polarized (LCP) light for _θ_ 

= +_Φ_(_x_, _y_)/2) and right circularly polarized (RCP) light for _θ_ = -_Φ_(_x_, _y_)/2)14,35. The metalens based on Eq. 2 functions only for circularly polarized (CP) light. To further

focus an LP light beam and control its polarization rotation by an angle \({\phi }_{n}\) at each focal point, the phase distribution is determined by34: $$\varPhi \left(x,y\right)={\rm{\arg

}}\left\{\mathop{\sum }\limits_{n=1}^{N}{(e}^{i[{\varphi }_{n}\left(x,y\right)+{\phi }_{n}]}+{e}^{-i{[\varphi }_{n}\left(x,y\right)-{\phi }_{n}]})\right\}$$ (3) For the design presented in

Eq. 3, all focal points appear on a single 3D polarization curve at a specific working wavelength _λ_. Going beyond previous attempts that focus on only one color26,27,28, we cascade

multiple wavelength-selective 3D polarization curves (such as 3D knots and digital numbers) at the same observation region. Consequently, the desired phase profile is determined by:

$$\varPhi \left(x,y\right)={\rm{\arg }}\left\{\mathop{\sum }\limits_{m=1}^{M}\mathop{\sum }\limits_{n=1}^{{N}_{m}}{(e}^{i[{\varphi }_{m,n}\left(x,y\right)+{\phi }_{m,n}]}+{e}^{-i{[\varphi

}_{m,n}\left(x,y\right)-{\phi }_{m,n}]})\right\}$$ (4) where \({\varphi }_{m,n}\left(x,y\right)=-\frac{2{\rm{\pi }}}{{\lambda

}_{m}}\left(\sqrt{{f}_{m,n}^{2}+{\left(x-{x}_{m,n}\right)}^{2}+{\left(y-{y}_{m,n}\right)}^{2}}-\sqrt{{f}_{m,n}^{2}+{x}_{m,n}^{2}+{y}_{m,n}^{2}}\,\right)\), _M_ and _N__m_ denote the number

of polarization curves and total number of points on the _m__th_ polarization curve, respectively. \({\lambda }_{m}\) represents the designed wavelength for the _m__th_ polarization curve.

\({(x}_{m,n}{,y}_{m,n},{f}_{m,n})\) and \({\phi }_{m,n}\) represent the 3D coordinates and polarization rotation angle of the _n__th_ focal point on the _m__th_ curve, respectively. THE

CASCADED POLARIZATION CAGES WITH A SINGLE COLOR To validate the design strategy, we begin with a metasurface M1 to experimentally demonstrate the cascaded polarization cages at a single

operation wavelength _λ_ = 650 nm (Fig. 2a). Here, we select six 2-foil knots with different sizes and geometric rotation angles to create the cascaded 3D cages. These six 3D knots share the

same central coordinates. The coordinates for the _n_th point on the _m_th 3D knots are determined by: $$\left\{\begin{array}{ll}{x}_{m,n}=-1.5{a}_{m}\sin (2{\alpha }_{m,n})\sin {\gamma

}_{m}+3{a}_{m}\sin {\alpha }_{m,n}\cos {\gamma }_{m}\\ {y}_{m,n}=-1.5{a}_{m}\sin (2{\alpha }_{m,n})({-\cos \gamma }_{m})+3{a}_{m}\sin {\alpha }_{m,n}\sin {\gamma }_{m}\\

{f}_{m,n}=-{a}_{m}\cos {\alpha }_{m,n}+f\end{array}\right.$$ (5) where the parameter _a__m_ controls the size of the knots and is set as 10 μm for three big 2-foil knots (_m_ = 1, 2, 3) to

construct the big 3D cage, and 5 μm for three small 2-foil knots (_m_ = 4, 5, 6) to create the embedded small 3D cage (Fig. 2a). The geometric rotation angle of the knots \({\gamma }_{m}\)

is set as 0 for the knots 1 and 4 (_m_ = 1, 4), π/3 for the knots 2 and 5 (_m_ = 2, 5) and 2π/3 (_m_ = 3, 6). The central focal plane of these six knots is defined by _f_ = 500 μm. The polar

angle \({\alpha }_{m,n}\) varies between 0 and 2π. To ensure the continuity of different focal curves, the total number of points \({N}_{m}\) on the knots is designed as \({N}_{m}=\,\)1300

(_m_ = 1, 2, 3) for three big knots, and \({N}_{m}=\,\)1000 (_m_ = 4, 5, 6) for three small knots, respectively. The initial polarization rotation angles are set to \({\phi }_{m,n}\) \(=\)

\({\rm{\pi }}/2\) for the focal points on the big cage (big knots), and\(\,{\phi }_{m,n}=\) \(0\) for the focal points on the small cage (small knots), as indicated by the black arrows in

Fig. 2b. The phase profile of metasurface M1, calculated and illustrated in Fig. 2c (top), is achieved using a metasurface composed of 1333×1333 gold nanorods. As shown in Fig. 2c (bottom),

each nanorod, with uniform dimensions of 40 nm in height, 80 nm in width, and 200 nm in length, sits on an indium tin oxide (ITO)-coated glass substrate. The period keeps at 300 nm along

both _x_ and _y_ directions. Details regarding the unit cell design and the efficiency analysis of the metasurface are given in Supplementary Section 1. The correlation between the focusing

efficiency of the metasurface and the number of focal points is detailed in Supplementary Section 2. The fabrication details are provided in the Methods Section. A tunable supercontinuum

laser (NKT Photonics SuperK EXTREME) is used as the light source to test the metasurfaces. A linear polarizer (LP1) and a quarter wave plate (QWP1) are used to generate the incident light

with CP states. Another combination of a quarter wave plate (QWP2) and a polarizer (analyzer, LP2), positioned behind an objective, is used to filter out the non-converted portion of the

light under the CP light illumination. An incident light beam with various linear polarization states is realized by removing the QWP1 and rotating the LP1. The cascaded polarization cages

can be observed using the analyzer LP2 upon the LP light illumination. Detailed descriptions of the experimental setup and design are provided in Supplementary Section 3 and Supplementary

Section 4, respectively. In this paper, the simulations for the cascaded polarization cages are performed using the Fresnel−Kirchhoff diffraction integral36. Figure 2d displays the

simulation results and experimental measurements of the cascaded 3D cages at three observation planes of _z_ = 490 μm, 500 μm, and 510 μm, under the RCP light illumination at _λ_ = 650 nm.

As shown in Fig. 2d, both the big and small 3D cages composed of six different 2-foil knots are simultaneously generated within the same spatial region. In addition, the intensity patterns

exhibit noticeable variations across different observation planes, verifying the 3D nature of the generated cascaded polarization cages. The 3D polarization distributions on the cascaded

polarization cages under the LP light illumination can be further revealed by observing the modulated intensity patterns with an analyzer. The transmission axis of the analyzer (red arrows

in Fig. 3) is kept perpendicular to the polarization direction of incident LP light (blue arrows in Fig. 3), which can filter out the nonconverted part. Figure 3a and b show the simulation

results and experimental measurements at three distinct observation planes (_z_ = 490 μm, 500 μm and 510 μm) for incident LP light beams with varying polarization directions: _β_ = 0 (Fig.

3a) and _β_ = π/4 (Fig. 3b). Here, _β_ represents the incident linear polarization direction relative to the _x_ axis. We can see from Fig. 3 that the polarization distributions on the

cascaded polarization cages are dynamically modified by changing the incident linear polarization direction. The lowest intensity (dark region) of cascaded polarization cages occurs at the

initial polarization rotation angles \(\phi =\)2_β_ and 2_β_ + \({\rm{\pi }}\,\)(see Supplementary Section 4 for a more detailed explanation). Therefore, for \(\beta =0\), the locations with

\(\phi =0\) corresponding to the small 3D cage disappear, as shown in Fig. 3a. Similarly, for \(\beta ={\rm{\pi }}/4\) in Fig. 3b, the dark region appears at the locations of the big 3D

cage where \(\phi =\) \({\rm{\pi }}/2\). The close alignment between simulation results and experimental measurements provides compelling evidence for the dynamic control of cascaded

polarization cages, enabling high security level for information encryption. THE CASCADED POLARIZATION CAGES WITH TWO COLORS To expand the encoding space, we introduce additional wavelengths

in the design of the metasurface M2 to generate multispectral cascaded polarization cages. Here, the big 3D cage is encoded with a wavelength of _λ__m_ = 650 nm, while the small 3D cage

embedded in the big cage is encoded with a wavelength of _λ__m_ = 510 nm. The initial polarization distributions on the cascaded polarization cages are set according to the previous design

of M1: \({\phi }_{m,n}\) \(=\) \({\rm{\pi }}/2\) for the big 3D cage (indicated by blue arrows in Fig. 4a), and\(\,{\phi }_{m,n}=\) \(0\) for the small 3D cage (indicated by black arrows in

Fig. 4a). Figure 4b–d show simulation and experimental results of the cascaded multispectral polarization cages with varying incident polarization states: RCP for Fig. 4b, and LP for Fig. 4c

and d. Under the RCP light illumination at dual wavelengths of _λ_ = 650 nm and 510 nm, the big red cage and small cyan cage are generated simultaneously at the middle observation plane of

_z_ = 500 μm (1st column in Fig. 4b). The simulated and measured results at other observation planes further demonstrate the existence of the 3D polarization cages (details provided in

Supplementary Section 5). Under single-wavelength illumination at _λ_ = 650 nm (2nd column in Fig. 4b) or _λ_ = 510 nm (2nd column in Fig. 4b), only the big red cage or small cyan cage can

be observed, demonstrating the wavelength-selective functionality of the designed metasurfaces due to the dispersion effect. With an incident LP light beam, the evolution of polarization

distributions is observed by gradually changing the incident polarization directions. For example, regions corresponding to the cascaded cages with the polarization rotation angle \(\phi\) =

 0 (small 3D cage), or π/2 (big 3D cage) disappear when the incident polarization direction is set to \(\beta =0\) (Fig. 4c) or \(\beta ={\rm{\pi }}/4\) (Fig. 4d), respectively. The

experimental results validate the metasurface’s capability to create cascaded multispectral polarization cages, closely aligning with theoretical predictions. DISCUSSION Various encryption

objects, encoded with customized polarization and color information can be concealed within the big 3D polarization cage. This encrypted information can only be decoded by observing

modulated intensity distributions using the correct combined key, which includes the incident LP state, transmission direction of the analyzer, incident wavelength, and observation region.

To demonstrate this encryption technology, an encrypted number consisting of seven polarization segments is hidden within the 3D polarization cage, as shown in Fig. 5a. Each segment is 12 μm

in length and comprises 300 focal spots (_N__m_ = 300). The initial polarization rotation angle and wavelength for the 3D polarization cage are set as \({\phi }_{m,n}\) = π/2 and _λ__m_ = 

650 nm, consistent with previous 3D cage designs. The seven polarization segments forming the number “8” are encoded with a wavelength of _λ__m_ = 532 nm and predesigned polarization

rotation angles to create a special encrypted number “5”. Specifically, the polarization rotation angles for the seven segments are set to \({\phi }_{m,n}\) = π/2 for the two vertical

segments at the top right and bottom right, and \({\phi }_{m,n}\) = 0 for the other five segments. As schematically illustrated in Fig. 5b, the encrypted number “5” can be decoded with the

correct key, including the incident LP state (blue arrow), the transmission direction of the analyzer (red arrow), incident wavelength (_λ_ = 532 nm), and observation distance (_z_ = 500

μm), which function as a key. The corresponding simulated and measured intensity distributions using this customized key are depicted in the bottom middle panel of Fig. 5d, verifying the

decoded process. To demonstrate the high security of this optical encryption system, the simulated and measured intensity distributions by using other combinations of incident LP state (blue

arrow), the transmission direction of the analyzer (red arrow), incident wavelength (_λ_) and observation distance (_z_) are also shown in other panels of Fig. 5d. These intensity

distributions differ significantly from the encrypted information (number “5” in the bottom middle panel of Fig. 5d). Simulated and measured light intensity patterns of the cascaded

polarization number and polarization cage at two wavelengths of 650 nm and 532 nm are presented in Supplementary Section 6.1. The simulated intensity distributions at other observation

planes for the example in Fig. 5 are provided in Supplementary Section 6.2. Compared with the other encryption schemes with a single polarization number37 and a single-color polarization

knot27 at one central coordinate based on metasurfaces, the proposed method utilizes the combination of the multispectral encrypted polarization structure and polarization cage to achieve an

enlarged encoding space, dramatically increasing the information capacity and security. Although the design strategy in this work shares some similarities with that in our previous

works28,29, this work represents the first demonstration of the multispectral polarization cages with unique property, which go beyond the conventional 3D polarization structures and hold

potential applications in many fields such as anti-counterfeiting and encryption. To conclude, we report the first demonstration of cascading multiple 3D polarization curves with different

colors based on a geometric metasurface. Cascaded multispectral 3D polarization cages, including a big red polarization cage and an embedded small cyan polarization cage are generated at the

same observation region. These cascaded 3D polarization cages are dynamically manipulated by adjusting the incident linear polarization states and wavelengths of the incident light. Figure

5 showcases the simulation results and experimental measurement for the information encryption utilizing the combination of the multispectral polarization number and 3D polarization cage.

Unlike the previous work26,27,28, where each polarization curve includes a single color at the observation region, multiple colors, and cascading technology are included in this design. Our

design can realize various polarization structures within the same 3D observation regions by manipulating the incident LP state, the transmission axis of the analyzer, and the incident

wavelength. In this work, the cascaded polarization cages encode a maximum of two wavelengths and polarization states, but this number can be further increased to enhance the information

capacity. Under the illumination of incident light with different incident polarization states, the simulation results of intensity distributions in the cascaded polarization cages with a

linear relation between \({\phi }_{m,n}\) and \({\alpha }_{m,n}\) (each cage is encoded with three wavelengths of 500 nm, 580 nm, and 650 nm) are detailed in Supplementary Section 7. This

approach integrates 3D polarization generation, multiple colors, and cascading technology, providing extra degrees of freedom for metasurface design and enabling small-volume polarization

systems for engineering 3D vector beams and optical encryption. METHODS All metasurfaces are composed of gold nanorods oriented at various angles on an ITO-coated glass substrate. These

metasurfaces are fabricated with standard electron beam lithography and lift-off process. Each metasurface occupies an area of 399×399 μm2. First, the substrate undergoes cleaning with

acetone in an ultrasonic bath for 10 minutes, followed by isopropyl alcohol (IPA) for another 10 minutes. Subsequently, the substrate is baked on a hotplate at 180 °C for 5 minutes. A

polymethyl methacrylate (PMMA) 950 A2 resist is spin-coated onto the substrate at 1000 rpm for 60 seconds to generate a PMMA film with a thickness of 120 nm. Nanopatterns are defined using

electron beam lithography (Raith PIONEER, 30 KV, 12 pA). After the electron beam exposure, the resist film is developed in a mixture of MIBK:IPA (1:3) for 45 seconds, and then rinsed with

IPA for 45 seconds. An electron beam evaporator is used to deposit a gold film with a thickness of 40 nm on the developed PMMA patterns. Finally, the required metasurface is ready for

testing following the lift-off process in acetone for 10 hours. DATA AVAILABILITY No datasets were generated or analysed during the current study. REFERENCES * Muelas-Hurtado, R. D. et al.

Observation of polarization singularities and topological textures in sound waves. _Phys. Rev. Lett._ 129, 204301 (2022). ADS  Google Scholar  * Bauer, T. et al. Observation of optical

polarization Möbius strips. _Science_ 347, 964–966 (2015). ADS  MATH  Google Scholar  * Luttmann, M. et al. Nonlinear up-conversion of a polarization Möbius strip with half-integer optical

angular momentum. _Sci. Adv._ 9, eadf3486 (2023). MATH  Google Scholar  * Dorn, R., Quabis, S. & Leuchs, G. Sharper focus for a radially polarized light beam. _Phys. Rev. Lett._ 91,

233901 (2003). ADS  Google Scholar  * Thiruarul, D., Charles, J. W., Lavanya, M., Rajesh, K. B. & Jaroszewicz, Z. Generation of multiple focal patterns via phase modulated radial and

azimuthal variant vector beam. _Opt. Quant. Electron._ 55, 395 (2023). Google Scholar  * Larocque, H. et al. Reconstructing the topology of optical polarization knots. _Nat. Phys._ 14, 1079

(2018). MATH  Google Scholar  * Kuznetsov, N. Y., Ryadchenko, A. E., Grigoriev, K. S. & Makarov, V. A. Knots and links of polarization singularity lines of light under tight focusing

with a parabolic mirror. _Phys. Rev. A._ 107, 063506 (2023). ADS  MathSciNet  Google Scholar  * Peng, C. et al. Patterning of lyotropic chromonic liquid crystals by photoalignment with

photonic metamasks. _Adv. Mater_ 29, 1606112 (2017). Google Scholar  * Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. _Science_

334, 333 (2011). ADS  MATH  Google Scholar  * Chen, X. et al. Dual-polarity plasmonic metalens for visible light. _Nat. Commun._ 3, 1198 (2012). ADS  MATH  Google Scholar  * Arbabi, A.,

Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. _Nat.

Nanotechnol._ 10, 937 (2015). ADS  Google Scholar  * Yu, N. & Capasso, F. Flat optics with designer metasurfaces. _Nat. Mater._ 13, 139–150 (2014). ADS  MATH  Google Scholar  *

Engelberg, J. & Levy, U. The advantages of metalenses over diffractive lenses. _Nat. Commun._ 11, 1991 (2020). ADS  MATH  Google Scholar  * Ahmed, H. et al. Multichannel superposition of

grafted perfect vortex beams. _Adv. Mater._ 34, 2203044 (2022). Google Scholar  * Wang, S. et al. A broadband achromatic metalens in the visible. _Nat. Nanotechnol._ 13, 227 (2018). ADS 

MATH  Google Scholar  * Jiang, Q. et al. Multiwavelength achromatic metalens in visible by inverse design. _Adv. Opt. Mater._ 11, 2300077 (2023). Google Scholar  * Zheng, R. et al. Active

multiband varifocal metalenses based on orbital angular momentum division multiplexing. _Nat. Commun._ 13, 4292 (2022). ADS  MATH  Google Scholar  * Ansari, M. A. et al. A spin-encoded

all-dielectric metahologram for visible light. _Laser Photonics Rev_. 13, 1900065 (2019). ADS  Google Scholar  * Kim, I. et al. Pixelated bifunctional metasurface driven dynamic vectorial

holographic color prints for photonic security platform. _Nat. Commun._ 12, 3614 (2021). ADS  MATH  Google Scholar  * Pan, K. et al. Cylindrical Vector Beam Holography without Preservation

of OAM Modes. _Nano Lett_. 24, 6761 (2024). ADS  MATH  Google Scholar  * Yin, Y. et al. Multi-Dimensional Multiplexed Metasurface Holography by Inverse Design. _Adv. Mater._ 36, 2312303

(2024). Google Scholar  * Ahmed, H. et al. Dynamic control of hybrid grafted perfect vector vortex beams. _Nat. Commun._ 14, 3915 (2023). ADS  MATH  Google Scholar  * Zhang, X. et al.

Multiplexed Generation of Generalized Vortex Beams with On‐Demand Intensity Profiles Based on Metasurfaces. _Laser Photonics Rev_. 16, 2100451 (2022). ADS  Google Scholar  * Wang, R. et al.

Compact multi-foci metalens spectrometer. _Light: Sci. Appl._ 12, 103 (2023). ADS  MATH  Google Scholar  * Faraji-Dana, M. et al. Compact folded metasurface spectrometer. _Nat. Commun._ 9,

4196 (2018). ADS  Google Scholar  * Wang, R. et al. Metalens for generating a customized vectorial focal curve. _Nano Lett_ 21, 2081 (2021). ADS  MATH  Google Scholar  * Li, Y. et al.

Longitudinally variable 3D optical polarization structures. _Sci. Adv._ 9, eadj6675 (2023). ADS  Google Scholar  * Intaravanne, Y. et al. Color-selective three-dimensional polarization

structure. _Light: Sci. Appl._ 11, 302 (2022). ADS  MATH  Google Scholar  * Li, Y. et al. Multiple Multicolored 3D Polarization Knots Arranged along Light Propagation. _ACS photonics_ 11,

4380 (2024). Google Scholar  * Cao, Y., Tang, L., Li, J., Lee, C. & Dong, Z. G. Multiplexing optical images for steganography by single metasurfaces. _Small_ 19, 2206319 (2023). MATH 

Google Scholar  * Ji, J. et al. High-dimensional Poincaré beams generated through cascaded metasurfaces for high-security optical encryption. _PhotoniX_ 5, 13 (2024). MATH  Google Scholar  *

Song, M. et al. Enabling optical steganography, data storage, and encryption with plasmonic colors. _Laser Photonics Rev_. 15, 202000343 (2021). ADS  Google Scholar  * Wang, G. et al.

Creating Multispectral Grafted Perfect Vector Vortex Beams in a Queue. _Laser Photonics Rev_. 18, 2400323 (2024). Google Scholar  * Zang, X. et al. A multi‐foci metalens with

polarization‐rotated focal points,. _Laser Photonics Rev_. 13, 1900182 (2019). ADS  MATH  Google Scholar  * Huang, L. et al. Dispersionless phase discontinuities for controlling light

propagation. _Nano Lett_. 12, 5750–5755 (2012). ADS  MATH  Google Scholar  * Zhang, Y., Liu, W., Gao, J. & Yang, X. Generating focused 3D perfect vortex beams by plasmonic metasurfaces.

_Adv. Opt. Mater._ 6, 1701228 (2018). Google Scholar  * Intaravanne, Y., Ansari, M. A., Ahmed, H. & Chen, X. Creating Wavelength‐Selective Polarization Digital Numbers,. _Adv. Opt.

Mater._ 12, 2203097 (2024). Google Scholar  Download references ACKNOWLEDGEMENTS This project was funded by the Engineering and Physical Sciences Research Council (EP/P029892/1), the

Leverhulme Trust (RPG-2021-145 and RPG-2023-283), the Special Plan for Basic Research Projects of Colleges and Universities in Henan Province (23ZX018), Key Scientific and Technological

Projects of Henan Province (242102520007 and 242102230072), Innovation and Entrepreneurship Training Programme for University Students (202410485056 and 202410485041), and Special Project

for Improving the Innovation Ability of Discipline Foundation of Zhengzhou University of Aeronautics (XKZX24129). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institute of Photonics and

Quantum Sciences, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK Yan Li, Muhammad Afnan Ansari, Hammad Ahmed & Xianzhong Chen * School of

Materials, Zhengzhou University of Aeronautics, Zhengzhou, 450015, China Yan Li & Facheng Zhong Authors * Yan Li View author publications You can also search for this author inPubMed 

Google Scholar * Muhammad Afnan Ansari View author publications You can also search for this author inPubMed Google Scholar * Hammad Ahmed View author publications You can also search for

this author inPubMed Google Scholar * Facheng Zhong View author publications You can also search for this author inPubMed Google Scholar * Xianzhong Chen View author publications You can

also search for this author inPubMed Google Scholar CONTRIBUTIONS X.C. and Y.L. initiated the idea. Y.L. conducted the numerical simulations. M.A.A. and H.A. fabricated the samples. Y.L.,

M.A.A, F. Z., and H.A. performed the measurements. Y.L., X.C., and M.A.A. prepared the manuscript. X.C. supervised the project. All the authors discussed and analyzed the results.

CORRESPONDING AUTHOR Correspondence to Xianzhong Chen. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN

ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and

reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you

modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in

this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Li, Y., Ansari, M.A., Ahmed, H. _et al._

Cascading multispectral polarization cages. _npj Nanophoton._ 2, 12 (2025). https://doi.org/10.1038/s44310-025-00056-7 Download citation * Received: 17 November 2024 * Accepted: 15 January

2025 * Published: 03 April 2025 * DOI: https://doi.org/10.1038/s44310-025-00056-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative