Integrating statistical physics and machine learning for combinatorial optimization

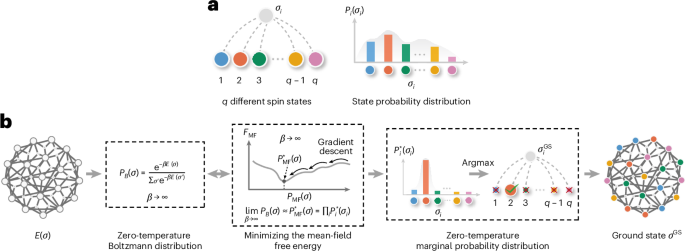
We introduce free-energy machine (FEM), an efficient and general method for solving combinatorial optimization problems. FEM combines free-energy minimization from statistical physics with

gradient-based optimization techniques in machine learning and utilizes parallel computation, outperforming state-of-the-art algorithms and showcasing the synergy of merging statistical

physics with machine learning. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your

institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $29.99 / 30 days cancel any time Learn more Subscribe to this journal

Receive 12 digital issues and online access to articles $99.00 per year only $8.25 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy

now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer

support REFERENCES * Arora, S. & Barak, B. _Computational Complexity: A Modern Approach_ (Cambridge Univ. Press, 2009). THIS BOOK PROVIDES AN IN-DEPTH INTRODUCTION TO COMPUTATIONAL

COMPLEXITY THEORY, EXAMINING THE COMPLEXITY OF CHALLENGES SUCH AS COMBINATORIAL OPTIMIZATION. * Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware solvers of

combinatorial optimization problems. _Nat. Rev. Phys._ 4, 363–379 (2022). THIS REVIEW EXAMINES ISING MACHINES, SPANNING QUANTUM, CLASSICAL, AND HYBRID APPROACHES AND COMPARES THEIR

PERFORMANCE. Article  Google Scholar  * Lucas, A. Ising formulations of many NP problems. _Front. Phys._ 2, 5 (2014). THIS PAPER PROVIDES ISING FORMULATIONS FOR MANY NON-DETERMINISTIC

POLYNOMIAL-TIME (NP)-COMPLETE AND NP-HARD PROBLEMS, DEMONSTRATING HOW TO MAP THESE COMPLEX PROBLEMS INTO THE ISING MODEL FRAMEWORK. * Charbonneau, P. et al. (eds) _Spin Glass Theory and Far

Beyond: Replica Symmetry Breaking After 40 Years_ (World Scientific, 2023). THIS BOOK OFFERS A COMPREHENSIVE OVERVIEW OF THE WIDE-RANGING APPLICATIONS OF SPIN GLASS THEORY, INCLUDING

INSIGHTS INTO THE USE OF THE MEAN-FIELD APPROXIMATION FAMILY. * Bilbro, G. et al. Optimization by mean field annealing. In _Advances in Neural Information Processing Systems_ (ed. Touretzky,

D.) (Morgan Kaufmann, 1988). THE PAPER INTRODUCES MEAN FIELD ANNEALING, A DETERMINISTIC OPTIMIZATION TECHNIQUE THAT ACCELERATES COMBINATORIAL PROBLEM-SOLVING BY REPLACING DISCRETE VARIABLES

WITH CONTINUOUS AVERAGES, ACHIEVING SEVERAL ORDERS OF MAGNITUDE FASTER CONVERGENCE THAN STOCHASTIC SIMULATED ANNEALING. Download references ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. THIS IS A SUMMARY OF: Shen, Z.-S. et al. Free-energy machine for combinatorial

optimization. _Nat. Comput. Sci_. https://doi.org/10.1038/s43588-025-00782-0 (2025). RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Integrating

statistical physics and machine learning for combinatorial optimization. _Nat Comput Sci_ 5, 277–278 (2025). https://doi.org/10.1038/s43588-025-00794-w Download citation * Published: 26

March 2025 * Issue Date: April 2025 * DOI: https://doi.org/10.1038/s43588-025-00794-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative