The role of stacking fault tetrahedra on void swelling in irradiated copper

ABSTRACT A long-standing and critical issue in the field of irradiated structural materials is that void swelling is significantly higher in face-centered cubic-structured (fcc) materials

(1% dpa−1) as compared to that of body-centered cubic-structured (bcc) materials (0.2% dpa−1). Despite extensive research in this area, the underlying mechanism of the difference in swelling

resistance between these two types of materials is not yet fully understood. Here, by combining atomistic simulations and STEM imaging, we find stacking fault tetrahedra (SFTs) are the

primary cause of the high swelling rate in pure fcc copper. We reveal that SFTs in fcc copper are not neutral sinks, different from the conventional knowledge. On the contrary, they are

highly biased compared to other types of sinks because of the SFT-point defect interaction mechanism. SFTs show strong absorption of mobile self-interstitial atoms (SIAs) from the faces and

vertices, and weak absorption of mobile vacancies from the edges. We compare the predicted swelling rates with experimental findings under varying conditions, demonstrating the distinct

contributions of each type of sink. These findings will contribute to understanding the swelling of irradiated structural materials, which may facilitate the design of materials with high

swelling resistance. SIMILAR CONTENT BEING VIEWED BY OTHERS DISLOCATION LOOP BIAS AND VOID SWELLING IN IRRADIATED Α-IRON FROM MESOSCALE AND ATOMISTIC SIMULATIONS Article Open access 06 May

2023 IRRADIATION RESISTANCE MECHANISM OF THE COCRFEMNNI EQUIATOMIC HIGH-ENTROPY ALLOY Article Open access 12 January 2021 COMPACT A15 FRANK-KASPER NANO-PHASES AT THE ORIGIN OF DISLOCATION

LOOPS IN FACE-CENTRED CUBIC METALS Article Open access 25 May 2023 INTRODUCTION Void swelling at intermediate temperatures, occurring at approximately 0.3−0.6 of the melting temperature, is

widely observed in structural materials exposed to high levels of particle radiation1,2,3,4. Such a phenomenon leads to significant effects that result in unacceptable volumetric changes,

degraded mechanical performance, and a limited lifetime of structural components in nuclear reactors4,5,6,7 and other extreme environments, such as space vehicles8. Furthermore, the

underlying cause—defect interaction in materials—is a critical focus in numerous significant fields, such as high entropy alloys9, energy storage materials10, and perovskites11. One critical

observation is that swelling rates are generally much higher in fcc materials as compared to bcc materials5,6,12,13, with a few exceptions14. Because of the critical significance of such

differences, the underlying reason has received significant attention and generated extensive discussions in recent decades. However, a conclusive explanation is yet to be established15,

although multiple mechanisms have been proposed by previous studies. Among these mechanisms, defect accumulation and the effect of microstructures in irradiated bcc and fcc metals has

garnered the most attention16. Previous studies17,18 indicate that to create the same level of defect density, Fe requires a dose that is two to three orders of magnitude higher than Cu.

Additionally, the difference in defect clustering during the thermal spike phase between fcc and bcc metals19 has been suggested as a contributing factor, but a fundamental understanding of

how these factors influence the swelling behavior has not been established. Some other effects, like the glissile self-interstitial atom (SIA) cluster removal mechanism13,20,21, which

affects the survival fraction of defects from displacement cascades22, are also considered. Nevertheless, none of the models are capable of reproducing the experimental values of swelling

rates at different temperatures in irradiated materials. Moreover, microstructural features, such as dislocations, act as the sinks of mobile point defects4, and the bias model23,24 has been

established to quantify the void swelling. Specifically, dislocation bias has been extensively discussed4,23,24,25,26, but the difference between bias factors obtained in fcc and bcc

materials cannot fully explain their swelling rate difference. Nevertheless, it is clear that the effect of microstructural features is the critical factor to investigate these phenomena,

and the model to study swelling behaviors must consider the types and densities of the sinks formed during the irradiations. However, due to the complexity of irradiation conditions,

identifying the primary underlying cause of the observed difference in swelling behavior between fcc and bcc materials presents a significant challenge. Among all the major types of

microstructural features in fcc Cu, this study identifies SFTs (mostly between 1.5 and 3.5 nm27,28,29) as a significant cause of the swelling rate differences between fcc and bcc materials,

based on state-of-the-art mesoscale and atomistic kinetic Monte Carlo (AKMC) simulations30,31. SFTs have been long considered neutral sinks for vacancy and SIA point defect absorption due to

the low elastic strain associated with the stair-rod dislocations that comprise the SFT periphery32. We observe both perfect and non-perfect SFTs27 to be non-neutral sinks that prefer to

absorb mobile SIAs over mobile vacancies in fcc copper. Such a phenomenon is due to the underlying mechanism of the SFT-point defect interaction, showing strong absorption of mobile SIAs

from the faces and vertices of the SFT, and weak absorption of mobile vacancies from the edges of the SFT. This mechanism leads to higher bias values of SFTs compared to other types of sinks

in irradiated copper26, including straight dislocations (both edge and screw types), 1/3<111> interstitial loops, and voids. The high bias values of SFTs, coupled with high number

densities (higher than 1022 m−3 based on experimental observations under 600 K12,28,29,33,34,35,36), collectively result in the high sink strength of SFTs. We further analyze the effects of

each type of sink on void swelling phenomena based on the obtained sink strengths and predicted swelling rates and compare computational results with a large number of neutron- or

ion-irradiation experiments, with different irradiation conditions and material microstructures12,29,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49. We demonstrate that SFTs are the

primary cause of high swelling rates in irradiated fcc copper and play a decisive role in creating the observed differences in swelling rates between general fcc and bcc structural

materials. These findings challenge traditional beliefs that SFTs do not act as biased sinks in irradiated fcc materials. Moreover, the insights gained from this study represent a

significant step towards understanding the roles of different sinks on swelling behavior, which in turn can inform the development of materials with enhanced swelling resistance. For

example, one possible approach to achieve improved swelling tolerance could involve reducing the density of small SFTs (≤3.5 nm in size), e.g. through tuning stacking fault energies or

compositional complexity. Additionally, increasing the initial dislocation density by cold working will also influence the swelling behavior of fcc materials. These strategies could

potentially lead to the development of more robust fcc structural materials capable of withstanding high-dose irradiations and being more resistant to irradiation-induced swelling. RESULTS

AND DISCUSSION MECHANISMS OF SFT-POINT DEFECT INTERACTIONS The mechanism of SFT-point defect interaction was quantified from statistical analysis of the diffusion behavior of mobile point

defects near an SFT. Contrasting behavior occurred for SIAs and vacancies due to the varying stress/strain field in the matrix surrounding the SFT. We find that mobile SIAs are absorbed at

the faces and vertices of SFTs, corresponding to regions with tensile strains; mobile single vacancies are absorbed at the edges of SFTs, corresponding to regions with compressive strains.

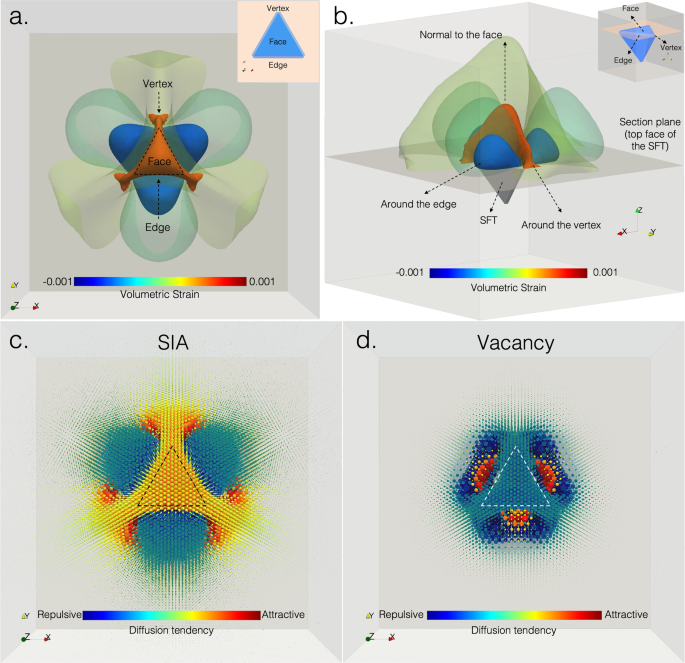
The volumetric strain map of a 2 nm SFT is shown in Fig. 1a, b, where regions under tension appear in red and are normal to the faces and around vertices of the SFT, and regions under

compression appear in blue and are normal to the SFT edges. Such a pattern persists over long distances (greater than 10 nm) and is indicated in light yellow and light blue. Please note

that, as the strain fields are identical on each face of the SFT, only the top face has been chosen to clearly illustrate the 3-D properties. The schematic representation of this is depicted

in Fig. 1b (from another angle of Fig. 1a). To clearly represent the varying SFT-point defect interaction, we depict the diffusion tendency of point defects around a 2 nm SFT in Fig. 1c, d

for SIAs and vacancies, respectively. Diffusion tendency was obtained based on KMC simulations at 100 K, showing the expected diffusion direction and its probability of a mobile point defect

at every atomic position near the SFT. The simulation at 100 K captures the key diffusion direction produced during irradiation at higher temperatures. Here, the expected diffusion

direction is represented by the vector sum of the diffusive steps taken from a given atomic position, and the probability corresponds to the length of this resultant vector relative to the

combined lengths of all diffusive step vectors. To enhance the clarity of the figure, such vectors are represented using spheres. In Fig. 1c, the attractive (tensile) regions (labeled in

yellow and red) show the diffusion direction of SIAs toward the SFT, and the repulsive regions are labeled in green and blue. The size of the sphere represents the probability of an SIA

diffusing along that pathway, showing a consistent tendency but a weaker effect over long ranges. The magnitude of the interaction with the SFT is much weaker for vacancies than that for

SIAs. Figure 1d shows that the SFT-vacancy interaction is very strong only at very short ranges (1−2 nm). Attractive pathways are found within 1 nm next to the edges of SFTs; conversely,

repulsive pathways are predominant at many geometric locations for the SFT-vacancy interaction. This contrasting interaction behavior, along with the high SFT number densities observed in

irradiated Cu that shortens the average distance between mobile point defects and SFTs, leads to a high effectiveness of SFTs as a sink for mobile SIAs in copper. This observed mechanism can

explain the results of several previous experimental studies and theoretical calculations. SFTs were originally suggested to collapse by absorbing a sufficient number of SIAs32,50 in

irradiated fcc materials. Later, the annihilation of SFTs as a result of irradiation was confirmed by in-situ observations in fcc materials51,52, and the growth/shrinkage mechanisms were

attributed to the absorption of mobile point defects27,50. Here, we observed a high preference for SFTs to absorb SIAs over vacancies, which will lead to significant shrinkage of SFTs. This

observation further clarifies why SFTs rarely grow beyond 3.5 nm in size as they form in cascades. Additionally, a possible growth mechanism involving migration and coalescence of small SFTs

(15-vacancy SFT) was proposed by Martinez et al.53 based on molecular dynamic (MD) simulations between 600 K and 1000 K. EXPERIMENTAL SFT LATTICE STRAIN MEASUREMENT SFTs appear as bright

triangular shapes when imaged along a \(\left\langle 110\right\rangle\) zone axis by low-angle annular dark-field scanning transmission electron microscopy (LAADF-STEM) (Fig. 2a), indicating

the possible presence of strain54. Local lattice strain in the plane perpendicular to the incident beam direction can be determined by tracking changes in Bragg disk positions in

convergent-beam electron diffraction (CBED) patterns (Fig. 2c) as a function of real space STEM probe position. Two-dimensional maps of strain can therefore be produced by measuring Bragg

disk shifts in a rectangular array of positions across the sample. Here, we used a novel 4D-STEM method with exit-wave power-cepstrum (EWPC) analysis55, which is robust to small sample

mis-tilts and reciprocal space intensity variations such as those caused by dynamical diffraction, to extract strain information from such an array of CBED patterns (Fig. 2c). As Fig. 2b

illustrates, experimental EWPC-STEM data of dual-ion-irradiated copper reveals a distribution of tensile areal strain (approximately \({\varepsilon }_{{xx}}\) + \({\varepsilon }_{{yy}}\))

inside and surrounding an SFT. For comparison with the results of the simulation in Fig. 1, a rotation was applied to match the experimental orientation and averaging the strain within the

thickness that encompassed the entire tetrahedral SFT in the \(\left[1\bar{1}0\right]\) direction (Fig. 2f). The resulting areal strain distribution (Fig. 2e) qualitatively matches the

experimental strain map (Fig. 2b) fairly well, given the additional experimental noise and sub-nm in-plane spatial resolution, showing higher tensile strain in the upper left SFT vertex than

the two others, and reduced stress immediately outside of this vertex. Additionally, the dependence of SFT strain field on size is qualitatively similar, although the predicted spatial

extent of the strain field will be lessened for smaller SFTs. One difference between the experimental and simulated results is that the two other vertices also exhibit a tensile strain in

the experimental results, while they do not in the simulated results (Fig. 2e), which may be due to the finite probe size or differences in averaging mechanisms. Quantitatively, the maximum

experimental and simulated tensile areal strains are on the same order of magnitude as well, at approximately 3.5% and 1.5%, respectively. Our simulation did not account for the influence of

helium (which can be generated in a real nuclear reactor environment from nuclear transmutation reactions) on the SFT strain field, however, which could potentially increase the strain

induced through pressure effects. The differences in strain distribution observed in the experimental and simulated results for the two vertices on the right (Fig. 2b, e) and the overall

maximum strain differences may therefore also be related to implantation of helium atoms in the experimental sample. Despite these small differences, EWPC-STEM strain mapping lends support

to the findings of the simulation, indicating that SFT’s have a relatively large tensile strain and therefore an affinity for mobile SIAs. SFT BIAS AND COMPARISON WITH OTHER SINKS The

mechanisms of SFT-point defect interactions lead to the preferential absorption of mobile SIAs over vacancies, which is termed bias. We quantified the bias values of SFTs, dislocation loops,

and straight dislocations using the same AKMC approach. Both bias equations and the AKMC framework are elaborated in the Methods Section. The results are shown in Fig. 3 and demonstrate

that the bias for both perfect and imperfect SFTs is the highest among all major sinks that exist in irradiated copper. Since SFT sizes observed in neutron-irradiated copper are mostly

between 1.5 nm and 3.5 nm based on experimental observations27,28,29, the bias values of 1.5 nm, 2 nm, and 3.5 nm perfect SFTs (with 21, 36, and 105 vacancies) were calculated and are shown

in Fig. 3a. Within the experimentally observed SFT number densities in the void swelling temperature regime (between 1018 m−3 and 1023 m−3,12,28,29,42,56,57), the perfect SFT bias is found

between 0.54 and 0.75. The bias decreases with rising temperatures from 573 K to 673 K and decreases with increasing SFT sizes from 1.5 nm to 3.5 nm. Such size dependence is also supported

by a previous binding energy calculation58. For non-perfect SFTs, we select an intermediate size of approximately 2 nm (with 32 vacancies) for our calculation. The bias values of non-perfect

SFTs are found to be between 0.36 and 0.38 at the same temperature and density range as the perfect SFTs, shown in Fig. 3a. Our results reveal a significantly lower bias of non-perfect SFTs

compared to perfect SFTs at the same size, temperature, and number density. This phenomenon can be attributed to the inability of non-perfect SFTs to form four vertices as perfect SFTs do.

Since this study has demonstrated that vertices play a critical role in absorbing mobile SIAs and repulsing mobile vacancies, the absorption region of mobile SIAs is thus much smaller in

non-perfect SFTs than in perfect ones. The bias of a 1/3<111 > {111} interstitial loop was calculated to be around 0.1 between 573 K and 673 K as shown in Fig. 3a. Since the typical

diameter of loops is larger than 5 nm and increases up to ~30 nm with increasing irradiation doses in experiments29,33,59,60, a 10 nm loop was employed in this study. Similarly, the

dislocation bias values of both edge and screw types were found to be much lower than those of SFTs, labeled in yellow and green bands in Fig. 3b. Edge dislocation bias is shown between 0.08

and 0.1 with the commonly reported dislocation density between 1012 m−2 and 1013 m−2 in experiments12,29,34,35,36,41,42,43,44,61. Plus, it is not sensitive to the temperature change from

473 K to 773 K, during which the swelling phenomenon occurs. The obtained bias for edge dislocations is in good agreement with previous works, including atomistic simulations by Chang et

al.62, elasticity theory calculations by Skinner et al.63 and Fisher et al.64, and the production bias model by Golubov et al.59. Alternatively, Wolfer20, Seif et al.65, and Sivak et al.66

reported relatively high dislocation bias values around 0.3. However, the highest edge dislocation bias listed above is still lower than that of SFTs. In comparison, screw dislocation bias

exhibits much lower bias values, ranging from −0.04 to 0.02 as the temperature is raised from 473 K to 773 K. The negative values were also reported by Sivak et al.66, suggesting that screw

dislocations in fcc copper are less effective at absorbing mobile SIAs compared to edge dislocations. Detailed bias values from 473 K to 773 K for all major sinks are provided in

Supplementary Fig. 7 to 12. SWELLING RATES AND EFFECTS OF MAJOR SINKS The swelling rate in irradiated copper is determined by calculating the sink strength of all major sinks, as elaborated

in the Methods Section. The obtained results are compared with experimentally reported swelling rates under irradiations12,29,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49, as shown in

Fig. 4, where they are plotted as a function of irradiation temperature. These experimental results cover a wide range of conditions, including irradiation doses from 0.001 dpa to 150 dpa,

and temperatures between 473 K and 802 K. We examine the contributions of each type of sink to the swelling phenomena and subsequently identify three primary scenarios. The violet curve

represents the SFT-dominant scenario (i), the blue curve stands for the loop-dominant scenario (ii), and the green curve corresponds to the dislocation-dominant scenario (iii). The predicted

swelling rates in these scenarios are calculated based on the sink strength of SFTs, loops, dislocations, and voids. The equations for sink strengths and swelling rates are provided in the

Methods Section. Each scenario illustrated in Fig. 4 is derived based on the fitted sink density of experimental observations12,29,33,34,35,36,42,43,44,47,57,61. These fitted sink densities

are represented by dotted lines in Fig. 5a–c for SFTs, loops, and dislocations, respectively. The fitted void density and size are provided in Supplementary Figs. 5 and 6. In Scenario (i),

SFTs serve as the dominant sink, corresponding to the upper limit of swelling rates (~1% dpa-1) in neutron-irradiated copper. This scenario typically occurs under 600 K, at which the high

densities of SFTs are observed in experiments (around 1022 m-3 or more)12,28,29,33,34,35,36, as shown in Fig. 4. In this scenario, the sink strengths of SFTs for SIAs are mostly higher than

1013 m-2 (Fig. 5a), which are higher than those of straight dislocations (Fig. 5c). Such high SFT sink strengths are due to the calculated high bias values and the experimentally observed

high SFT number densities under 600 K (>1021 m-3). The high number densities reduce the average distance between mobile point defects and SFTs, thereby enabling SFTs to absorb mobile SIAs

more efficiently. This remains true even though the impact range and sink strength of a single SFT are smaller than those of a loop or a straight dislocation (details in Supplementary Fig. 

1). The high density of SFTs can be attributed to high probability for direct formation within energetic displacement cascades. This is generally considered a result of the low stacking

fault energy (SFE) in fcc copper27,35. With increasing temperatures, SFTs will annihilate due to their interaction with mobile SIAs or thermally evaporations50. This leads to the

experimentally observed decrease of SFT densities with increasing temperatures57. Additionally, the impact of non-perfect SFTs on the predicted swelling rate is also estimated and the bias

values are found to be close to those of perfect SFTs, which are substantially higher than those of other types of sinks. The swelling rates in scenario (ii) exhibit a close agreement with

the average values of experimental observations (from around 0.1 to 0.5% dpa-1)12,29,33,34,35,36,37,38,39,40,41,42,43,44, as demonstrated by the blue curve in Fig. 4. The 1/3 < 111 > 

{111} interstitial loop is assumed as the governing type of sink in this scenario, the sink strengths of which are normally higher than those of straight dislocations, as demonstrated in

Fig. 5b. The presence of loops, compared with scenario (i), reduces the swelling rate under 700 K. For instance, the swelling rates observed by Zinkle et al.29 and Singh et al.33,34,35 under

600 K in Fig. 4 (circled in orange) are lower than the predicted swelling rates that only consider SFTs. Here, the collective effect of the low bias dislocation loops with their number

densities (generally higher than 1020 m-3 under 600 K29,42,57) is evident in experimental observations. Notably, the number density of both SFTs and dislocation loops decreases with

increasing temperature, leading to a weaker effect of scenarios (i) and (ii) at high temperatures under a void swelling regime. In scenario (iii), the contribution of straight dislocations

on the swelling rates prevails, especially at high temperatures (approximately above 700 K). This dislocation-dominant scenario represents the predicted lower limit of the swelling rates of

irradiated copper. The sink strengths of dislocations decrease not as much as those of SFTs or loops with increasing temperatures (as shown in Fig. 4c). These temperature-insensitive sink

strengths can be attributed to the stable dislocation densities observed in experiments, mostly ranging between 1012 and 1013 m-2, 12,29,34,35,36,41,42, with only a few experiments reporting

higher dislocation densities (over 1013 m-2)43,44,61. Comparatively, the number densities and sink strengths of SFTs and loops decrease significantly with increasing temperatures based on

experimental observations29,41,57,61. Thus, the role of dislocations in the swelling phenomena observed in fcc copper is more consistent than that of SFTs and loops. Furthermore, since

dislocation bias values alone cannot fully explain the observed differences in swelling rates between bcc and fcc materials, it is possible that SFTs are the primary factor determining these

swelling rate differences. Additionally, at such high temperatures, vacancy evaporations impact swelling phenomena significantly22,67,68, which takes place from the void surface. When the

temperature is lower than 548 K, no more than 10% of the vacancies in voids will evaporate; yet this ratio reaches 60% when the temperature is 771 K. The equations for evaporation rate

calculations are provided in Supplementary Note 1 and Supplementary Fig. 4. Additional experimental data is summarized in Supplementary Figs. 2 and 3 as a reference. METHODS CONSTRUCTION OF

SINKS AND STRAIN CALCULATIONS The construction of the sinks was performed using the LAMMPS molecular dynamics code69 with interatomic potential developed by Mishin et al.70. Perfect SFTs

with 1.5 nm, 2.0 nm, and 3.5 nm in size were formed by relaxing a triangular 1/3<111> vacancy loop containing 21, 36, and 105 vacancies, respectively. A non-perfect SFT with a size of

~2 nm (containing 32 vacancies) was generated from a perfect 2 nm SFT (containing 36 vacancies) by absorbing four mobile SIAs. The 1/3<111> interstitial dislocation loop of 10 nm size

was set up with 223 inserted SIAs on the <111> plane. The 10 nm void was built up by removing 44115 atoms in a spherical shape. The coordinates were \([1\bar{1}0]\), \([11\bar{2}]\),

and \([111]\) for the simulation boxes of sinks above, with periodic boundary conditions in all directions. Both the edge and screw dislocations were 1/2<110>{111} type, which

dissociated into two 1/6<112> partial dislocations. The strain fields were calculated using OVITO71 visualization and analysis code. ATOMISTIC KINETIC MONTE CARLO (AKMC) The bias of

different types of sinks was calculated using a recently developed AKMC approach30,31, the scheme of which is shown in Fig. 6. The KMC processes of point defect diffusion starts from the

spherical surface of the simulation system, where the distance to the center of the biased sink remains the same. The lifetime of a point defect, which is defined as the time required to

diffuse from an initial position to a sink, was then calculated based on the KMC simulation. The time of point defect diffusion to the first nearest neighbor depends on the migration energy

barriers (MEBs), which are mostly calculated using SEAKMC72,73. Dipole tensor method65,74 was employed to calculate the MEBs far from the sink30. Detailed approaches for the MEB calculation

are provided in Supplementary Note 2 and the results are shown from Supplementary Figs. 13–28. The bias based on the lifetime is derived,

$${Bias}=\frac{{Z}_{i}-{Z}_{v}}{{Z}_{v}}=\frac{\frac{{\tau }_{i}^{r}}{{\tau }_{i}}-\frac{{\tau }_{v}^{r}}{{\tau }_{v}}}{\frac{{\tau }_{v}^{r}}{{\tau }_{v}}}=\frac{{{\tau }_{i}^{r}\tau

}_{v}}{{{\tau }_{v}^{r}\tau }_{i}}-1,$$ (1) where \({\tau }_{i}\) and \({\tau }_{v}\) represents the lifetime of SIAs and vacancies, and the superscript \(r\) means random walk. \({Z}_{i}\)

and \({Z}_{v}\) stand for capture efficiencies of SIAs and vacancies to the sink22. Plus, the sink strength in the physical system75 is calculated using $${k}_{\alpha }^{2}={{Z}_{\alpha

}k}^{2},$$ (2) where \({{{{{\rm{\alpha }}}}}}\) is either \({{{{{\rm{i}}}}}}\) or \({{{{{\rm{v}}}}}}\), representing interstitials and vacancies, respectively. The sink strength without the

influence of the interaction between the sink and the point defect, \({k}^{2}\), is obtained during AKMC calculations, $${k}^{2}=\frac{2n}{{d}_{j}^{2}\langle {n}_{j}\rangle },$$ (3) where

_n_ is the dimensionality (_n_ = 3 in this study), \(\langle {n}_{j}\rangle\) is the average number of jumps of PDs, and \({d}_{j}\) is the jump distance76,77. Notably, the sink strength for

voids is obtained based on rate theory22, $${k}^{2}=4\pi \left\langle R\right\rangle \rho ,$$ (4) where \(\left\langle R\right\rangle\) represents the average void radius and \(\rho\) is

the void density. The reason to employ this equation is the significant impact of both void size and density on the sink strength. However, it is challenging to obtain accurate void sink

strength considering a wide range of sizes, especially considering the evidence that small voids are biased sinks for mobile point defects4,78,79,80,81,82. SWELLING RATE CALCULATION Swelling

rate calculation was derived22,30,83 and calculated based on the sink strength for comparison with experimental results. When considering only one type of sink, taking SFT as an example

(scenario (i)), $${Swelling}\,{rate}= \varepsilon

*\frac{{k}_{{Void},v}^{2}({k}_{{Void},i}^{2}+{k}_{{SFT},i}^{2})-{k}_{{Void},i}^{2}({k}_{{Void},v}^{2}+{k}_{{SFT},v}^{2})}{\left({k}_{{Void},v}^{2}+{k}_{{SFT},v}^{2}\right)\left({k}_{{Void},i}^{2}+{k}_{{SFT},i}^{2}\right)}\\

* \left(1-\frac{{J}_{v}^{{em}}}{N}\right).$$ (5) The term \({k}_{{sink},\alpha }^{2}\) represents the sink strength of a specific sink (void or SFT in this equation) in the ideal system.

Subscript \(\alpha\) can represent either interstitials with \(i\) or vacancies with \(v\), respectively. Survival fraction \(\varepsilon\) is selected to be 0.1 based on recent analyses to

correct for correlated defect recombination84. For scenarios (ii) and (iii), \({k}_{{SFT}}^{2}\) was replaced with the sink strength of loops and dislocations. \({J}_{v}^{{em}}\) is the

vacancy emission rate22,68, and \(N\) is the number of vacancies contained in a void. \({J}_{v}^{{em}}/N\) is the total volume loss rate of a void. DUAL-ION IRRADIATION OF POLYCRYSTALLINE

COPPER High-purity (99.99%) polycrystalline copper disks obtained from Johnson–Mathey were cold rolled to achieve a 50% reduction in thickness. Prior irradiation, the disks were mechanically

and electropolished at −40°C using a 33% HNO3/67% CH3OH solution with a 5 V applied potential. A thermocouple wire was spot welded to the back of the TEM disks to monitor the irradiation

temperature. Oak Ridge dual-beam Van de Graaff irradiation facilities85 were used for irradiation. Simultaneous dual-ion beam (4 MeV Fe & 0.2–0.4 MeV He ions) irradiation was conducted

at 440 °C, reaching a peak damage level of 13 dpa and helium concentration of 48 appm at a depth of approximately 1.2 μm, as calculated with _E_d = 30 eV for Cu according to SRIM 2013 Q-C

vacancy.txt method86. The total fluence of the Fe ion beam was 9.5\(\times\)1019, and the dose rate was 3.3\(\times\)10-3 dpa/s. The helium beam energy was ramped from 0.2 to 0.4 MeV at

0.025 Hz, resulting in uniform helium implantation at depths of 0.5–1.1 μm. STEM EXPERIMENTS The STEM imaging and 4D-STEM exit-wave power-cepstrum (EWPC) measurements were conducted using a

JEOL NEOARM aberration-corrected STEM operating at an acceleration voltage of 200 kV. Atomic-resolution STEM imaging was performed with a semi-convergence angle of ~13.6 mrad and 4D-STEM

data for EWPC measurements was acquired using a ~3.4 mrad semi-convergence angle, resulting in a probe diameter of <1 nm. CBED patterns were captured with the beam direction aligned along

a Cu \(\left\langle 1\bar{1}0\right\rangle\) zone axis on a pnCCD pixelated detector with a frame size of 264 × 264 pixels, an acquisition rate of 1000 frames per second, and at 512 × 512

real space probe positions. The data was binned by four in each real space dimension to increase the signal-to-noise ratio of the CBED patterns and by an additional two in each reciprocal

space dimension to enhance the data processing rate. Details of the EWPC method used to make lattice strain measurements are available in a separate report55 and related codes are available

at https://github.com/ElliotPadgett/PC-STEM. DATA AVAILABILITY The raw data (migration energy barriers) that supports the findings of this study are available in Figshare with the

https://doi.org/10.6084/m9.figshare.24480862. All the other data generated during and/or analyzed during the current study are available from the corresponding author upon reasonable

request. REFERENCES * Bhattacharya, A. & Zinkle, S. J. in _Comprehensive Nuclear Materials_ Vol. 1 (eds Konings, R. J. M. & Stoller, R. E.) 406–455 (Elsevier, 2020). * Cawthorne, C.

& Fulton, E. J. Voids in irradiated stainless steel. _Nature_ 216, 576–577 (1967). Article  Google Scholar  * Pugh, S. F. Voids formed by irradiation of reactor materials - report of

conference. _J. Br. Nucl. Energy Soc._ 10, 159 (1971). Google Scholar  * Mansur, L. K. Void swelling in metals and alloys under irradiation - assessment of theory. _Nucl. Technol._ 40, 5–34

(1978). Article  CAS  Google Scholar  * Zinkle, S. J. & Was, G. S. Materials challenges in nuclear energy. _Acta Mater._ 61, 735–758 (2013). Article  CAS  Google Scholar  * Garner, F.

A., Toloczko, M. B. & Sencer, B. H. Comparison of swelling and irradiation creep behavior of fcc-austenitic and bcc-ferritic/martensitic alloys at high neutron exposure. _J. Nucl.

Mater._ 276, 123–142 (2000). Article  CAS  Google Scholar  * Du, C. et al. Ultrastrong nanocrystalline steel with exceptional thermal stability and radiation tolerance. _Nat. Commun._ 9,

5389 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Eswarappa Prameela, S. et al. Materials for extreme environments. _Nat. Rev. Mater._ 8, 81–88 (2023). Article  Google

Scholar  * Zhang, Z. et al. Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi. _Nat. Commun._ 6, 10143 (2015). Article  CAS  PubMed  Google Scholar  * Gao, P. et

al. The critical role of point defects in improving the specific capacitance of delta-MnO2 nanosheets. _Nat. Commun._ 8, 14559 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar 

* Lee, W. et al. Perovskite microcells fabricated using swelling-induced crack propagation for colored solar windows. _Nat. Commun._ 13, 1946 (2022). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Zinkle, S. J. & Farrell, K. Void swelling and defect cluster formation in reactor-irradiated copper. _J. Nucl. Mater._ 168, 262–267 (1989). Article  CAS  Google Scholar

  * Golubov, S. I., Singh, B. N. & Trinkaus, H. Defect accumulation in fee and bcc metals and alloys under cascade damage conditions - towards a generalisation of the production bias

model. _J. Nucl. Mater._ 276, 78–89 (2000). Article  CAS  Google Scholar  * Matsui, H., Gelles, D. S. & Kohno, Y. Large swelling observed in a V-5atmospheric-percent Fe alloy after

irradiation in Fftf. _Eff. Radiat. Mater. 15th Int. Symp._ 1125, 928–941 (1992). Google Scholar  * Zinkle, S. J. & Snead, L. L. Designing radiation resistance in materials for fusion

energy. _Annu. Rev. Mater. Res._ 44, 241–267 (2014). Article  CAS  Google Scholar  * English, C. A. Low-dose neutron-irradiation damage in Fcc and Bcc metals. _J. Nucl. Mater._ 108, 104–123

(1982). Article  Google Scholar  * Victoria, M. et al. The microstructure and associated tensile properties of irradiated fcc and bcc metals. _J. Nucl. Mater._ 276, 114–122 (2000). Article 

CAS  Google Scholar  * Baluc, N. et al. A comparison of the microstructure and tensile behaviour of irradiated fcc and bcc metals. _Microstruct. Process. Irradiat. Mater._ 540, 539–548

(1999). CAS  Google Scholar  * Brailsford, A. D. & Bullough, R. Rate theory of swelling due to void growth in irradiated metals. _J. Nucl. Mater._ 44, 121–135 (1972). Article  CAS 

Google Scholar  * Wolfer, W. G. The dislocation bias. _J. Comput. Aided Mater. Des._ 14, 403–417 (2007). Article  CAS  Google Scholar  * Bullough, R., Eyre, B. L. & Krishan, K. Cascade

damage effects on swelling of irradiated materials. _Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci._ 346, 81–102 (1975). CAS  Google Scholar  * Golubov, S. I., Barashev, A. V. &

Stoller, R. E. Radiation damage theory. In _Comprehensive Nuclear Materials, Vol 1: Basic Aspects of Radiation Effects in Solids/Basic Aspects of Multi-Scale Modeling_ 357–391 (Elsevier,

2012). * Singh, B. N. & Evans, J. H. Significant differences in defect accumulation behavior between Fcc and Bcc crystals under cascade damage conditions. _J. Nucl. Mater._ 226, 277–285

(1995). Article  CAS  Google Scholar  * Trinkaus, H., Singh, B. N. & Foreman, A. J. E. Impact of glissile interstitial loop production in cascades on defect accumulation in the

transient. _J. Nucl. Mater._ 206, 200–211 (1993). Article  CAS  Google Scholar  * Osetsky, Y. N., Bacon, D. J., Gao, F., Serra, A. & Singh, B. N. Study of loop-loop and loop-edge

dislocation interactions in bcc iron. _J. Nucl. Mater._ 283, 784–788 (2000). Article  Google Scholar  * Xu, H. X., Osetsky, Y. N. & Stoller, R. E. Cascade annealing simulations of bcc

iron using object kinetic Monte Carlo. _J. Nucl. Mater._ 423, 102–109 (2012). Article  CAS  Google Scholar  * Schaublin, R., Yao, Z., Baluc, N. & Victoria, M. Irradiation-induced

stacking fault tetrahedra in fcc metals. _Philos. Mag._ 85, 769–777 (2005). Article  Google Scholar  * Yoshida, N., Akashi, Y., Kitajima, K. & Kiritani, M. Formation of secondary defects

in copper by 14 Mev neutron-irradiation and their effects on microstructure evolution. _J. Nucl. Mater._ 133, 405–409 (1985). Article  Google Scholar  * Zinkle, S. J. & Snead, L. L.

Microstructure of copper and nickel irradiated with fission neutrons near 230-degrees-C. _J. Nucl. Mater._ 225, 123–131 (1995). Article  CAS  Google Scholar  * Yu, Z. & Xu, H.

Dislocation loop bias and void swelling in irradiated α-iron from mesoscale and atomistic simulations. _Commun. Mater._ 4, 29 (2023). Article  CAS  Google Scholar  * Hao, J. N.,

Casillas-Trujillo, L. & Xu, H. X. Using lifetime of point defects for dislocation bias in bcc Fe. _Curr. Opin. Solid State Mater. Sci._ 26 101021 (2022). * Silcox, J. & Hirsch, P. B.

Direct observations of defects in quenched gold. _Philos. Mag._ 4, 72–89 (1959). Article  CAS  Google Scholar  * Singh, B. N., Leffers, T. & Horsewell, A. Dislocation and void

segregation in copper during neutron-irradiation. _Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop._ 53, 233–242 (1986). CAS  Google Scholar  * Singh, B. N., Horsewell, A.,

Toft, P. & Edwards, D. J. Temperature and dose dependencies of microstructure and hardness of neutron-irradiated Ofhc copper. _J. Nucl. Mater._ 224, 131–140 (1995). Article  CAS  Google

Scholar  * Singh, B. N., Eldrup, M., Horsewell, K., Ehrhart, P. & Dworschak, F. On recoil energy dependent void swelling in pure copper - part I. Experimental results. _Philos. Mag. A

Phys. Condens. Matter Struct. Defects Mech. Prop._ 80, 2629–2650 (2000). CAS  Google Scholar  * Mukouda, I. & Shimomura, Y. Damage evolution in neutron-irradiated Cu during neutron

irradiation. _J. Nucl. Mater._ 271, 230–235 (1999). Article  Google Scholar  * Brager, H. R. Effects of neutron-irradiation to 63 Dpa on the properties of various commercial copper-alloys.

_J. Nucl. Mater._ 141, 79–86 (1986). Article  Google Scholar  * Lee, T. S. et al. Microstructural evolution and swelling of high-strength, high conductivity Rs-Pm copper-alloys irradiated to

13.5 Dpa with neutrons. _J. Nucl. Mater._ 141-143, 179–183 (1986). Article  CAS  Google Scholar  * Livak, R. J., Zocco, T. G. & Hobbs, L. W. Neutron damage microstructures of

high-conductivity copper-alloys. _J. Nucl. Mater._ 144, 121–127 (1987). Article  CAS  Google Scholar  * Garner, F. A., Brager, H. R. & Anderson, K. R. Neutron-induced changes in density

and electrical-conductivity of copper-alloys at 16 to 98 Dpa and 430-degrees-C. _J. Nucl. Mater._ 179, 250–253 (1991). Article  Google Scholar  * Singh, B. N., Horsewell, A., Gelles, D. S.

& Garner, F. A. Void swelling in copper and copper-alloys irradiated with fission neutrons. _J. Nucl. Mater._ 191, 1172–1176 (1992). Article  Google Scholar  * Singh, B. N., Eldrup, M.,

Zinkle, S. J. & Golubov, S. I. On grain-size-dependent void swelling in pure copper irradiated with fission neutrons. _Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop._

82, 1137–1158 (2002). CAS  Google Scholar  * Muroga, T. & Yoshida, N. Microstructure of neutron-irradiated copper alloyed with nickel and zinc. _J. Nucl. Mater._ 212, 266–269 (1994).

Article  Google Scholar  * Watanabe, H. & Garner, F. A. Void swelling of pure copper, Cu-5ni and Cu-5mn alloys irradiated with fast-neutrons. _J. Nucl. Mater._ 212, 370–374 (1994).

Article  Google Scholar  * Brimhall, J. L. & Kissinger, H. E. Void formation in irradiated copper, nickel, and copper-nickel alloys. _Radiat. Effects: Inc. Plasma Sci. Plasma Technol._

15, 259–272 (1972). Article  CAS  Google Scholar  * Garner, F. A., Hamilton, M. L., Shikama, T., Edwards, D. J. & Newkirk, J. W. Response of solute and precipitation strengthened

copper-alloys at high neutron exposure. _J. Nucl. Mater._ 191, 386–390 (1992). Article  Google Scholar  * Muroga, T., Matue, T., Watanabe, H. & Yoshida, N. Void swelling of copper and

copper alloys induced by heavy ion irradiation. _Eff. Radiat. Mater. 18th Int. Symp._ 1325, 991–998 (1999). Google Scholar  * Yamakawa, K., Mukouda, I. & Shimomura, Y. Void formation in

neutron-irradiated Cu and Cu alloys. _J. Nucl. Mater._ 191, 396–400 (1992). Article  Google Scholar  * Zinkle, S. J. & Singh, B. N. Microstructure of Cu-Ni alloys neutron irradiated at

210 degrees C and 420 degrees C to 14 dpa. _J. Nucl. Mater._ 283, 306–312 (2000). Article  Google Scholar  * Singh, B. N., Golubov, S. I., Trinkaus, H., Edwards, D. J. & Eldrup, M.

Review: evolution of stacking fault tetrahedra and its role in defect accumulation under cascade damage conditions. _J. Nucl. Mater._ 328, 77–87 (2004). Article  CAS  Google Scholar  *

Ishino, S., Sekimura, N., Hirooka, K. & Muroga, T. Insitu observation of cascade damage in gold under heavy-ion irradiation at high-temperature. _J. Nucl. Mater._ 141, 776–780 (1986).

Article  Google Scholar  * Kiritani, M. et al. Formation of vacancy clustered defects from cascade collisions during heavy-ion irradiation and their annihilation by freely-migrating

interstitial atoms. _J. Nucl. Mater._ 212-215, 192–197 (1994). Article  CAS  Google Scholar  * Martínez, E. & Uberuaga, B. P. Mobility and coalescence of stacking fault tetrahedra in Cu.

_Sci. Rep._ 5, 9084 (2015). Article  PubMed  PubMed Central  Google Scholar  * Yu, Z. H., Muller, D. A. & Silcox, J. Study of strain fields at a-Si/c-Si interface. _J. Appl. Phys._ 95,

3362–3371 (2004). Article  CAS  Google Scholar  * Padgett, E. et al. The exit -wave power-cepstrum transform for scanning nanobeam electron diffraction: robust strain mapping at subnanometer

resolution and subpicometer precision. _Ultramicroscopy_ 214, 112994 (2020). Article  CAS  PubMed  Google Scholar  * Zinkle, S. J., Farrell, K. & Kanazawa, H. Microstructure and cavity

swelling in reactor-irradiated dilute copper-boron alloy. _J. Nucl. Mater._ 179, 994–997 (1991). Article  Google Scholar  * Singh, B. N. & Zinkle, S. J. Defect accumulation in pure fcc

metals in the transient regime - a review. _J. Nucl. Mater._ 206, 212–229 (1993). Article  CAS  Google Scholar  * Osetsky, Y. N., Serra, A., Victoria, M., Golubov, S. I. & Priego, V.

Vacancy loops and stacking-fault tetrahedra in copper - I. Structure and properties studied by pair and many-body potentials. _Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech.

Prop._ 79, 2259–2283 (1999). CAS  Google Scholar  * Golubov, S. I., Singh, B. N. & Trinkaus, H. On recoil-energy-dependent defect accumulation in pure copper - part II. Theoretical

treatment. _Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop._ 81, 2533–2552 (2001). CAS  Google Scholar  * Hirsch, P. B., Cotterill, R. M. J. & Jones, M. W. in _Proc. 5th

International Congress on Electron Microscopy_ (Academic Press, 1962). * Leffers, T., Singh, B. N., Buckley, S. N. & Manthorpe, S. A. Void-swelling in cold-worked copper during Hvem

irradiation. _J. Nucl. Mater._ 118, 60–67 (1983). Article  CAS  Google Scholar  * Chang, Z. W., Olsson, P., Terentyev, D. & Sandberg, N. Dislocation bias factors in fcc copper derived

from atomistic calculations. _J. Nucl. Mater._ 441, 357–363 (2013). Article  CAS  Google Scholar  * Skinner, B. C. & Woo, C. H. Shape effect in the drift diffusion of point-defects into

straight dislocations. _Phys. Rev. B_ 30, 3084–3097 (1984). Article  CAS  Google Scholar  * Fisher, S. B., White, R. J. & Miller, K. M. Quantitative-analysis of void swelling in pure

copper. _Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop._ 40, 239–255 (1979). CAS  Google Scholar  * Seif, D. & Ghoniem, N. M. Effect of anisotropy, SIA orientation, and

one-dimensional migration mechanisms on dislocation bias calculations in metals. _J. Nucl. Mater._ 442, S633–S638 (2013). Article  CAS  Google Scholar  * Sivak, A. B. & Sivak, P. A.

Efficiency of dislocations as sinks of radiation defects in fcc copper crystal. _Crystallogr. Rep._ 59, 407–414 (2014). Article  CAS  Google Scholar  * Was, G. S. _Fundamentals of Radiation

Materials Science: Metals and Alloys_ (Springer, 2007). * Barashev, A. V., Golubov, S. I., Osetsky, Y. N. & Stoller, R. E. Dissociation of migrating particle from trap with long-range

interaction field. _Philos. Mag._ 90, 907–921 (2010). Article  CAS  Google Scholar  * Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. _J. Comput. Phys._ 117, 1–19

(1995). Article  CAS  Google Scholar  * Mishin, Y., Mehl, M. J., Papaconstantopoulos, D. A., Voter, A. F. & Kress, J. D. Structural stability and lattice defects in copper: Ab initio,

tight-binding, and embedded-atom calculations. _Phys. Rev. B_ 63, 224106 (2001). Article  Google Scholar  * Stukowski, A. Visualization and analysis of atomistic simulation data with

OVITO-the Open Visualization Tool. _Model. Simul. Mater. Sci. Eng._ https://doi.org/10.1088/0965-0393/18/1/015012 (2010). * Xu, H. X., Osetsky, Y. N. & Stoller, R. E. Self-evolving

atomistic kinetic Monte Carlo: fundamentals and applications. _J. Phys. Condens. Mater._ https://doi.org/10.1088/0953-8984/24/37/375402 (2012). * Xu, H. X., Stoller, R. E., Beland, L. K.

& Osetsky, Y. N. Self-evolving atomistic kinetic Monte Carlo simulations of defects in materials. _Comp. Mater. Sci._ 100, 135–143 (2015). Article  CAS  Google Scholar  * Carpentier, D.,

Jourdan, T., Le Bouar, Y. & Marinica, M. C. Effect of saddle point anisotropy of point defects on their absorption by dislocations and cavities. _Acta Mater._ 136, 323–334 (2017).

Article  CAS  Google Scholar  * Mansur, L. K., Brailsford, A. D. & Wolfer, W. G. On the meaning of sink capture efficiency and sink strength for point-defects. _J. Nucl. Mater._ 105,

36–38 (1982). Article  CAS  Google Scholar  * Heinisch, H. L., Singh, B. N. & Golubov, S. I. The effects of one-dimensional glide on the reaction kinetics of interstitial clusters. _J.

Nucl. Mater._ 283, 737–740 (2000). Article  Google Scholar  * Malerba, L., Becquart, C. S. & Domain, C. Object kinetic Monte Carlo study of sink strengths. _J. Nucl. Mater._ 360, 159–169

(2007). Article  CAS  Google Scholar  * Dubinko, V. I., Ostapchuk, P. N. & Slezov, V. V. Theory of radiation-induced and thermal coarsening of the void ensemble in metals under

irradiation. _J. Nucl. Mater._ 161, 239–260 (1989). Article  CAS  Google Scholar  * Dubinko, V. I., Guglya, A. G. & Donnelly, S. E. Radiation-induced formation, annealing and ordering of

voids in crystals: theory and experiment. _Nucl. Instrum. Methods Phys. Res. Sec. B Beam Interact. Mater. At._ 269, 1634–1639 (2011). Article  CAS  Google Scholar  * Ayanoglu, M. &

Motta, A. T. Void shrinkage in 21Cr32Ni austenitic model alloy during in-situ ion irradiation. _J. Nucl. Mater._ 543, 152636 (2021). Article  CAS  Google Scholar  * Chen, Y. et al.

Damage-tolerant nanotwinned metals with nanovoids under radiation environments. _Nat. Commun._ 6, 7036 (2015). Article  CAS  PubMed  Google Scholar  * Niu, T. et al. Recent studies on void

shrinkage in metallic materials subjected to in situ heavy ion irradiations. _Jom_ 72, 4008–4016 (2020). Article  Google Scholar  * Mansur, L. K. Theory and experimental background on

dimensional changes in irradiated alloys. _J. Nucl. Mater._ 216, 97–123 (1994). Article  CAS  Google Scholar  * Zinkle, S. J. & Stoller, R. E. Quantifying defect production in solids at

finite temperatures: thermally-activated correlated defect recombination corrections to DPA (CRC-DPA). _J. Nuclear Mater._ https://doi.org/10.1016/j.jnucmat.2023.154292 (2023). * Zinkle, S.

J. Dual-ion irradiation of copper. 86–89 (ORNL report, 1987). * Lin, Y.-R., Zinkle, S. J., Ortiz, C. J., Webb, R. & Stoller, R. E. Predicting displacement damage for ion irradiation:

origin of the overestimation of vacancy production in SRIM full-cascade calculations. _Curr. Opin. Solid State Mater. Sci_. 27, 101120 (2023). Download references ACKNOWLEDGEMENTS This work

is supported by the US Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0019151. This research used resources of the National Energy Research Scientific

Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231. The scanning transmission

electron microscopy portion of this research was supported by the Center for Nanophase Materials Sciences (CNMS), which is a U.S. Department of Energy, Office of Science User Facility at Oak

Ridge National Laboratory (ORNL). This research was also funded by the US Department of Energy’s Fusion Materials Program at Oak Ridge National Laboratory, under the contract

DE-AC05-00OR22725 with UT-Battelle, LLC. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Materials Science and Engineering, The University of Tennessee, Knoxville, TN, 37996, USA

Ziang Yu, Steven J. Zinkle & Haixuan Xu * Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA Yan-Ru Lin & Steven J. Zinkle * Center

for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA Michael J. Zachman * Department of Nuclear Engineering, The University of Tennessee, Knoxville, TN,

37996, USA Steven J. Zinkle Authors * Ziang Yu View author publications You can also search for this author inPubMed Google Scholar * Yan-Ru Lin View author publications You can also search

for this author inPubMed Google Scholar * Michael J. Zachman View author publications You can also search for this author inPubMed Google Scholar * Steven J. Zinkle View author publications

You can also search for this author inPubMed Google Scholar * Haixuan Xu View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Ziang Yu:

Investigation, Methodology, Validation, Formal analysis, Writing – original draft, Visualization. Yan-Ru Lin: Experimental observation, Formal analysis, Writing – review & editing.

Michael J. Zachman: Experimental observation, Formal analysis, Writing – review & editing. Steven J. Zinkle: Methodology, Formal analysis, Writing – review & editing, Supervision.

Haixuan Xu: Conceptualization, Methodology, Formal analysis, Writing – review & editing, Supervision, Project administration, Funding acquisition. CORRESPONDING AUTHOR Correspondence to

Haixuan Xu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Materials_ thanks Weizhong Han and the

other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Xiaoyan Li and John Plummer. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIALS RIGHTS AND PERMISSIONS OPEN

ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format,

as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third

party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yu, Z., Lin, YR., Zachman, M.J. _et

al._ The role of stacking fault tetrahedra on void swelling in irradiated copper. _Commun Mater_ 5, 53 (2024). https://doi.org/10.1038/s43246-024-00491-7 Download citation * Received: 28

December 2023 * Accepted: 03 April 2024 * Published: 16 April 2024 * DOI: https://doi.org/10.1038/s43246-024-00491-7 SHARE THIS ARTICLE Anyone you share the following link with will be able

to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative