Maximum diffusion reinforcement learning

ABSTRACT Robots and animals both experience the world through their bodies and senses. Their embodiment constrains their experiences, ensuring that they unfold continuously in space and

time. As a result, the experiences of embodied agents are intrinsically correlated. Correlations create fundamental challenges for machine learning, as most techniques rely on the assumption

that data are independent and identically distributed. In reinforcement learning, where data are directly collected from an agent’s sequential experiences, violations of this assumption are

often unavoidable. Here we derive a method that overcomes this issue by exploiting the statistical mechanics of ergodic processes, which we term maximum diffusion reinforcement learning. By

decorrelating agent experiences, our approach provably enables single-shot learning in continuous deployments over the course of individual task attempts. Moreover, we prove our approach

generalizes well-known maximum entropy techniques and robustly exceeds state-of-the-art performance across popular benchmarks. Our results at the nexus of physics, learning and control form

a foundation for transparent and reliable decision-making in embodied reinforcement learning agents. Access through your institution Buy or subscribe This is a preview of subscription

content, access via your institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access

subscription $29.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 12 digital issues and online access to articles $119.00 per year only $9.92 per issue Learn more

Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS:

* Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS PRESERVING AND COMBINING KNOWLEDGE IN ROBOTIC LIFELONG

REINFORCEMENT LEARNING Article Open access 05 February 2025 MECHANICAL INTELLIGENCE FOR LEARNING EMBODIED SENSOR-OBJECT RELATIONSHIPS Article Open access 15 July 2022 MASTERING DIVERSE

CONTROL TASKS THROUGH WORLD MODELS Article Open access 02 April 2025 DATA AVAILABILITY Data supporting the findings of this study are available via Zenodo at

https://doi.org/10.5281/zenodo.10723320 (ref. 71). CODE AVAILABILITY Code supporting the findings of this study is available via Zenodo at https://doi.org/10.5281/zenodo.10723320 (ref. 71).

REFERENCES * Degrave, J. et al. Magnetic control of tokamak plasmas through deep reinforcement learning. _Nature_ 602, 414–419 (2022). Article  Google Scholar  * Won, D.-O., Müller, K.-R.

& Lee, S.-W. An adaptive deep reinforcement learning framework enables curling robots with human-like performance in real-world conditions. _Sci. Robot._ 5, eabb9764 (2020). Article 

Google Scholar  * Irpan, A. Deep reinforcement learning doesn’t work yet. _Sorta Insightful_ www.alexirpan.com/2018/02/14/rl-hard.html (2018). * Henderson, P. et al. Deep reinforcement

learning that matters. In _Proc. 32nd AAAI Conference on Artificial Intelligence_ (eds McIlraith, S. & Weinberger, K.) 3207–3214 (AAAI, 2018). * Ibarz, J. et al. How to train your robot

with deep reinforcement learning: lessons we have learned. _Int. J. Rob. Res._ 40, 698–721 (2021). Article  Google Scholar  * Lillicrap, T. P. et al. _Proc. 4th_ _International Conference on

Learning Representations_ (ICLR, 2016). * Haarnoja, T., Zhou, A., Abbeel, P. & Levine, S. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic

actor. In _Proc. 35th International Conference on Machine Learning_ (eds Dy, J. & Krause, A.) 1861–1870 (PMLR, 2018). * Plappert, M. et al. _Proc. 6th_ _International Conference on

Learning Representations_ (ICLR, 2018). * Lin, L.-J. Self-improving reactive agents based on reinforcement learning, planning and teaching. _Mach. Learn._ 8, 293–321 (1992). Article  Google

Scholar  * Schaul, T., Quan, J., Antonoglou, I. & Silver, D. _Proc. 4th_ _International Conference on Learning Representations_ (ICLR, 2016). * Andrychowicz, M. et al. Hindsight

experience replay. In _Proc. Advances in Neural Information Processing Systems_ _30_ (eds Guyon, I. et al.) 5049–5059 (Curran Associates, 2017). * Zhang, S. & Sutton, R. S. A deeper look

at experience replay. Preprint at https://arxiv.org/abs/1712.01275 (2017). * Wang, Z. et al. _Proc. 5th_ _International Conference on Learning Representations_ (ICLR, 2017). * Hessel, M. et

al. Rainbow: combining improvements in deep reinforcement learning. In _Proc. 32nd_ _AAAI Conference on Artificial Intelligence_ (eds McIlraith, S. and Weinberger, K.) 3215–3222 (AAAI

Press, 2018). * Fedus, W. et al. Revisiting fundamentals of experience replay. In _Proc. 37th_ _International Conference on Machine Learning_ (eds Daumé III, H. & Singh, A.) 3061–3071

(JMLR.org, 2020). * Mnih, V. et al. Human-level control through deep reinforcement learning. _Nature_ 518, 529–533 (2015). Article  Google Scholar  * Ziebart, B. D., Maas, A. L., Bagnell, J.

A. & Dey, A. K. Maximum entropy inverse reinforcement learning. In _Proc. 23rd AAAI Conference on Artificial Intelligence_ (ed. Cohn, A.) 1433–1438 (AAAI, 2008). * Ziebart, B. D.,

Bagnell, J. A. & Dey, A. K. Modeling interaction via the principle of maximum causal entropy. In _Proc._ _27th International Conference on Machine Learning_ (eds Fürnkranz, J. &

Joachims, T.) 1255–1262 (Omnipress, 2010). * Ziebart, B. D. _Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy._ PhD thesis, Carnegie Mellon Univ. (2010). *

Todorov, E. Efficient computation of optimal actions. _Proc. Natl Acad. Sci. USA_ 106, 11478–11483 (2009). Article  Google Scholar  * Toussaint, M. Robot trajectory optimization using

approximate inference. In _Proc._ _26th International Conference on Machine Learning_ (eds Bottou, L. & Littman, M.) 1049–1056 (ACM, 2009). * Rawlik, K., Toussaint, M. & Vijayakumar,

S. On stochastic optimal control and reinforcement learning by approximate inference. In _Proc._ _Robotics: Science and Systems VIII_ (eds Roy, N. et al.) 353–361 (MIT, 2012). * Levine, S.

& Koltun, V. Guided policy search. In _Proc. 30th International Conference on Machine Learning_ (eds Dasgupta, S. & McAllester, D.) 1–9 (JMLR.org, 2013). * Haarnoja, T., Tang, H.,

Abbeel, P. & Levine, S. Reinforcement learning with deep energy-based policies. In _Proc. 34th International Conference on Machine Learning_ (eds Precup, D. & Teh, Y. W.) 1352–1361

(JMLR.org, 2017). * Haarnoja, T. et al. Learning to walk via deep reinforcement learning. In _Proc._ _Robotics: Science and Systems XV_ (eds Bicchi, A. et al.) (RSS, 2019). * Eysenbach, B.

& Levine, S. _Proc. 10th_ _International Conference on Learning Representations_ (ICLR, 2022). * Chen, M. et al. Top-K off-policy correction for a REINFORCE recommender system. In

_Proc._ _12th ACM International Conference on Web Search and Data Mining_ (eds Bennett, P. N. & Lerman, K.) 456–464 (ACM, 2019). * Afsar, M. M., Crump, T. & Far, B. Reinforcement

learning based recommender systems: a survey. _ACM Comput. Surv._ 55, 1–38 (2022). Article  Google Scholar  * Chen, X., Yao, L., McAuley, J., Zhou, G. & Wang, X. Deep reinforcement

learning in recommender systems: a survey and new perspectives. _Knowl. Based Syst._ 264, 110335 (2023). Article  Google Scholar  * Sontag, E. D. _Mathematical Control Theory: Deterministic

Finite Dimensional Systems_ (Springer, 2013). * Hespanha, J. P. _Linear Systems Theory_ 2nd edn (Princeton Univ. Press, 2018). * Mitra, D. W_-_matrix and the geometry of model equivalence

and reduction. _Proc. Inst. Electr. Eng._ 116, 1101–1106 (1969). Article  MathSciNet  Google Scholar  * Dean, S., Mania, H., Matni, N., Recht, B. & Tu, S. On the sample complexity of the

linear quadratic regulator. _Found. Comput. Math._ 20, 633–679 (2020). Article  MathSciNet  Google Scholar  * Tsiamis, A. & Pappas, G. J. Linear systems can be hard to learn. In _Proc._

_60th IEEE Conference on Decision and Control_ (ed. Prandini, M.) 2903–2910 (IEEE, 2021). * Tsiamis, A., Ziemann, I. M., Morari, M., Matni, N. & Pappas, G. J. Learning to control linear

systems can be hard. In _Proc. 35th Conference on Learning Theory_ (eds Loh, P.-L. & Raginsky, M.) 3820–3857 (PMLR, 2022). * Williams, G. et al. Information theoretic MPC for

model-based reinforcement learning. In _Proc._ _IEEE International Conference on Robotics and Automation_ (ed. Nakamura, Y.) 1714–1721 (IEEE, 2017). * So, O., Wang, Z. & Theodorou, E. A.

Maximum entropy differential dynamic programming. In _Proc._ _IEEE International Conference on Robotics and Automation_ (ed. Kress-Gazit, H.) 3422–3428 (IEEE, 2022). * Thrun, S. B.

_Efficient Exploration in Reinforcement Learning_. Technical report (Carnegie Mellon Univ., 1992). * Amin, S., Gomrokchi, M., Satija, H., van Hoof, H. & Precup, D. A survey of

exploration methods in reinforcement learning. Preprint at https://arXiv.org/2109.00157 (2021). * Jaynes, E. T. Information theory and statistical mechanics. _Phys. Rev._ 106, 620–630

(1957). Article  MathSciNet  Google Scholar  * Dixit, P. D. et al. Perspective: maximum caliber is a general variational principle for dynamical systems. _J. Chem. Phys._ 148, 010901 (2018).

Article  Google Scholar  * Chvykov, P. et al. Low rattling: a predictive principle for self-organization in active collectives. _Science_ 371, 90–95 (2021). Article  MathSciNet  Google

Scholar  * Kapur, J. N. _Maximum Entropy Models in Science and Engineering_ (Wiley, 1989). * Moore, C. C. Ergodic theorem, ergodic theory, and statistical mechanics. _Proc. Natl Acad. Sci.

USA_ 112, 1907–1911 (2015). Article  MathSciNet  Google Scholar  * Taylor, A. T., Berrueta, T. A. & Murphey, T. D. Active learning in robotics: a review of control principles.

_Mechatronics_ 77, 102576 (2021). Article  Google Scholar  * Seo, Y. et al. State entropy maximization with random encoders for efficient exploration. In _Proc. 38th_ _International

Conference on Machine Learning, Virtual_ (eds Meila, M. & Zhang, T.) 9443–9454 (ICML, 2021). * Prabhakar, A. & Murphey, T. Mechanical intelligence for learning embodied sensor-object

relationships. _Nat. Commun._ 13, 4108 (2022). Article  Google Scholar  * Chentanez, N., Barto, A. & Singh, S. Intrinsically motivated reinforcement learning. In _Proc. Advances in

Neural Information Processing Systems_ _17_ (eds Saul, L. et al.) 1281–1288 (MIT, 2004). * Pathak, D., Agrawal, P., Efros, A. A. & Darrell, T. Curiosity-driven exploration by

self-supervised prediction. In _Proc. 34th International Conference on Machine Learning_ (eds Precup, D. & Teh, Y. W.) 2778–2787 (JLMR.org, 2017). * Taiga, A. A., Fedus, W., Machado, M.

C., Courville, A. & Bellemare, M. G. _Proc. 8th_ _International Conference on Learning Representations_ (ICLR, 2020). * Wang, X., Deng, W. & Chen, Y. Ergodic properties of

heterogeneous diffusion processes in a potential well. _J. Chem. Phys._ 150, 164121 (2019). Article  Google Scholar  * Palmer, R. G. Broken ergodicity. _Adv. Phys._ 31, 669–735 (1982).

Article  Google Scholar  * Islam, R., Henderson, P., Gomrokchi, M. & Precup, D. Reproducibility of benchmarked deep reinforcement learning tasks for continuous control. Preprint at

https://arXiv.org/1708.04133 (2017). * Moos, J. et al. Robust reinforcement learning: a review of foundations and recent advances. _Mach. Learn. Knowl. Extr._ 4, 276–315 (2022). Article 

Google Scholar  * Strehl, A. L., Li, L., Wiewiora, E., Langford, J. & Littman, M. L. PAC model-free reinforcement learning. In _Proc. 23rd_ _International Conference on Machine Learning_

(eds Cohen, W. W. & Moore, A.) 881–888 (ICML, 2006). * Strehl, A. L., Li, L. & Littman, M. L. Reinforcement learning in finite MDPs: PAC analysis. _J. Mach. Learn. Res._ 10,

2413–2444 (2009). * Kirk, R., Zhang, A., Grefenstette, E. & Rocktäaschel, T. A survey of zero-shot generalisation in deep reinforcement learning. _J. Artif. Intell. Res._ 76, 201–264

(2023). Article  MathSciNet  Google Scholar  * Oh, J., Singh, S., Lee, H. & Kohli, P. Zero-shot task generalization with multi-task deep reinforcement learning. In _Proc. 34th

International Conference on Machine Learning_ (eds Precup, D. & Teh, Y. W.) 2661–2670 (JLMR.org, 2017). * Krakauer, J. W., Hadjiosif, A. M., Xu, J., Wong, A. L. & Haith, A. M. Motor

learning. _Compr. Physiol._ 9, 613–663 (2019). * Lu, K., Grover, A., Abbeel, P. & Mordatch, I. _Proc. 9th_ _International Conference on Learning Representations_ (ICLR, 2021). * Chen,

A., Sharma, A., Levine, S. & Finn, C. You only live once: single-life reinforcement learning. In _Proc. Advances in Neural Information Processing Systems 35_ (eds Koyejo, S. et al.)

14784–14797 (NeurIPS, 2022). * Ames, A., Grizzle, J. & Tabuada, P. Control barrier function based quadratic programs with application to adaptive cruise control. In _Proc. 53rd_ _IEEE

Conference on Decision and Control_ 6271–6278 (IEEE, 2014). * Taylor, A., Singletary, A., Yue, Y. & Ames, A. Learning for safety-critical control with control barrier functions. In

_Proc. 2nd Conference on Learning for Dynamics and Control_ (eds Bayen, A. et al.) 708–717 (PLMR, 2020). * Xiao, W. et al. BarrierNet: differentiable control barrier functions for learning

of safe robot control. _IEEE Trans. Robot._ 39, 2289–2307 (2023). * Seung, H. S., Sompolinsky, H. & Tishby, N. Statistical mechanics of learning from examples. _Phys. Rev. A_ 45,

6056–6091 (1992). Article  MathSciNet  Google Scholar  * Chen, C., Murphey, T. D. & MacIver, M. A. Tuning movement for sensing in an uncertain world. _eLife_ 9, e52371 (2020). Article 

Google Scholar  * Song, S. et al. Deep reinforcement learning for modeling human locomotion control in neuromechanical simulation. _J. Neuroeng. Rehabil._ 18, 126 (2021). Article  Google

Scholar  * Berrueta, T. A., Murphey, T. D. & Truby, R. L. Materializing autonomy in soft robots across scales. _Adv. Intell. Syst._ 6, 2300111 (2024). Article  Google Scholar  * Sutton,

R. S. & Barto, A. G. _Reinforcement Learning: An Introduction_ (MIT, 2018). * Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. _Nat. Methods_ 17,

261–272 (2020). Article  Google Scholar  * Berrueta, T. A., Pinosky, A. & Murphey, T. D. Maximum diffusion reinforcement learning repository. _Zenodo_

https://doi.org/10.5281/zenodo.10723320 (2024). Download references ACKNOWLEDGEMENTS We thank A. T. Taylor, J. Weber and P. Chvykov for their comments on early drafts of this work. We

acknowledge funding from the US Army Research Office MURI grant no. W911NF-19-1-0233 and the US Office of Naval Research grant no. N00014-21-1-2706. We also acknowledge hardware loans and

technical support from Intel Corporation, and T.A.B. is partially supported by the Northwestern University Presidential Fellowship. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department

of Mechanical Engineering, Northwestern University, Evanston, IL, USA Thomas A. Berrueta, Allison Pinosky & Todd D. Murphey Authors * Thomas A. Berrueta View author publications You can

also search for this author inPubMed Google Scholar * Allison Pinosky View author publications You can also search for this author inPubMed Google Scholar * Todd D. Murphey View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS T.A.B. derived all theoretical results, performed supplementary data analyses and control experiments,

supported RL experiments and wrote the manuscript. A.P. developed and tested RL algorithms, carried out all RL experiments and supported manuscript writing. T.D.M. secured funding and guided

the research programme. CORRESPONDING AUTHORS Correspondence to Thomas A. Berrueta or Todd D. Murphey. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests.

PEER REVIEW PEER REVIEW INFORMATION _Nature Machine Intelligence_ thanks the anonymous reviewers for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S

NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary

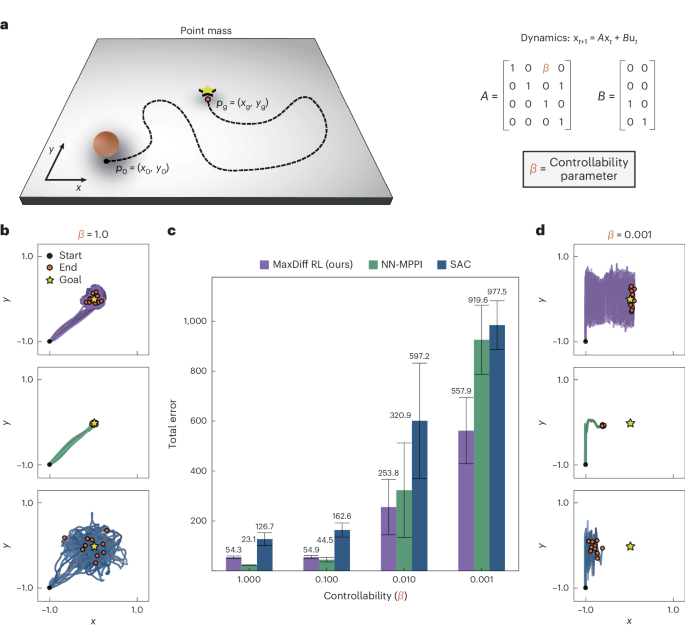
Notes 1–4, Tables 1 and 2 and Figs. 1–9. SUPPLEMENTARY VIDEO 1 Depicts an application of MaxDiff RL to MuJoCo’s swimmer environment. We explore the role of the temperature parameter’s

performance by varying it across three orders of magnitude. SUPPLEMENTARY VIDEO 2 Depicts an application of MaxDiff RL to MuJoCo’s swimmer environment, with comparisons to NN-MPPI and SAC.

The performance of MaxDiff RL does not vary across seeds. This is tested across two different system conditions: one with a light-tailed and more controllable swimmer and one with a

heavy-tailed and less controllable swimmer. SUPPLEMENTARY VIDEO 3 Depicts an application of MaxDiff RL to MuJoCo’s swimmer environment. We perform a transfer learning experiment in which

neural representations are learned on a system with a given set of properties and then deployed on a system with different properties. MaxDiff RL remains task-capable across agent

embodiments. SUPPLEMENTARY VIDEO 4 Depicts an application of MaxDiff RL to MuJoCo’s swimmer environment under a substantial modification. Agents cannot reset their environment, which

requires solving the task in a single deployment. First, representative snapshots of single-shot deployments are shown. A complete playback of an individual MaxDiff RL single-shot learning

trial is shown. Playback is staggered such that the first swimmer covers environment steps 1–2,000, the next one 2,001–4,000, and so on, for a total of 20,000 environment steps. RIGHTS AND

PERMISSIONS Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s);

author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law. Reprints and permissions ABOUT THIS

ARTICLE CITE THIS ARTICLE Berrueta, T.A., Pinosky, A. & Murphey, T.D. Maximum diffusion reinforcement learning. _Nat Mach Intell_ 6, 504–514 (2024).

https://doi.org/10.1038/s42256-024-00829-3 Download citation * Received: 03 August 2023 * Accepted: 19 March 2024 * Published: 02 May 2024 * Issue Date: May 2024 * DOI:

https://doi.org/10.1038/s42256-024-00829-3 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative