Quantum approximate bayesian computation for nmr model inference

ABSTRACT Recent technological advances may lead to the development of small-scale quantum computers that are capable of solving problems that cannot be tackled with classical computers. A

limited number of algorithms have been proposed and their relevance to real-world problems is a subject of active investigation. Analysis of many-body quantum systems is particularly

challenging for classical computers due to the exponential scaling of the Hilbert space dimension with the number of particles. Hence, solving the problems relevant to chemistry and

condensed-matter physics is expected to be the first successful application of quantum computers. In this Article, we propose another class of problems from the quantum realm that can be

solved efficiently on quantum computers: model inference for nuclear magnetic resonance (NMR) spectroscopy, which is important for biological and medical research. Our results are based on

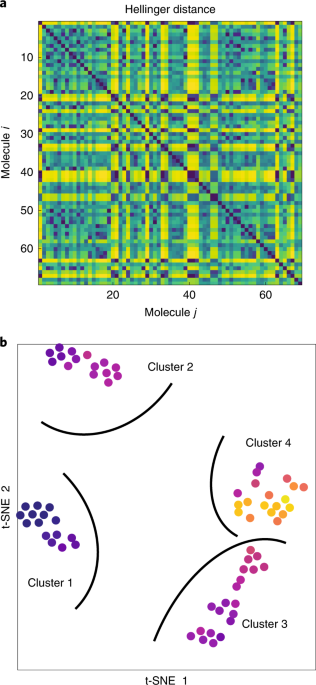
three interconnected studies. First, we use methods from classical machine learning to analyse a dataset of NMR spectra of small molecules. We perform stochastic neighbourhood embedding and

identify clusters of spectra, and demonstrate that these clusters are correlated with the covalent structure of the molecules. Second, we propose a simple and efficient method, aided by a

quantum simulator, to extract the NMR spectrum of any hypothetical molecule described by a parametric Heisenberg model. Third, we propose a simple variational Bayesian inference procedure

for estimating the Hamiltonian parameters of experimentally relevant NMR spectra. Access through your institution Buy or subscribe This is a preview of subscription content, access via your

institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $29.99 / 30 days cancel

any time Learn more Subscribe to this journal Receive 12 digital issues and online access to articles $119.00 per year only $9.92 per issue Learn more Buy this article * Purchase on

SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about

institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS ROBUST AUTOMATED BACKBONE TRIPLE RESONANCE NMR ASSIGNMENTS OF PROTEINS USING

BAYESIAN-BASED SIMULATED ANNEALING Article Open access 21 March 2023 OPTIMAL 13C NMR INVESTIGATION OF INTRINSICALLY DISORDERED PROTEINS AT 1.2 GHZ Article 12 December 2023 COMPUTATIONAL

MOLECULAR SPECTROSCOPY Article 27 May 2021 DATA AVAILABILITY The data and code to numerically generate the NMR data sets used in this manuscript can be found at

https://github.com/dsels/QuantumNMR. REFERENCES * Preskill, J. Quantum computing in the NISQ era and beyond. _Quantum_ 2, 79–98 (2018). Google Scholar  * Bernien, H. et al. Probing many-body

dynamics on a 51-atom quantum simulator. _Nature_ 551, 579–584 (2017). Google Scholar  * Friis, N. et al. Observation of entangled states of a fully controlled 20-qubit system. _Phys. Rev.

X_ 8, 021012 (2018). Google Scholar  * Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014). * Peruzzo,

A. et al. A variational eigenvalue solver on a photonic quantum processor. _Nat. Commun._ 5, 4213 (2014). Google Scholar  * Kokail, C. et al. Self-verifying variational quantum simulation

of lattice models. _Nature_ 569, 355–360 (2019). Google Scholar  * Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. _Nature_

549, 242–246 (2017). Google Scholar  * Colless, J. I. et al. Computation of molecular spectra on a quantum processor with an error-resilient algorithm. _Phys. Rev. X_ 8, 011021 (2018).

Google Scholar  * Diggle, P. J. & Gratton, R. J. Monte Carlo methods of inference for implicit statistical models. _J. R. Stat. Soc. B_ 46, 193–227 (1984). MathSciNet  MATH  Google

Scholar  * Beaumont, M. A., Zhang, W. & Balding, D. J. Approximate Bayesian computation in population genetics. _Genetics_ 162, 2025–2035 (2002). Google Scholar  * Gershenfeld, N. A.

& Chuang, I. L. Bulk spin-resonance quantum computation. _Science_ 275, 350–356 (1997). MathSciNet  MATH  Google Scholar  * Braunstein, S. L. et al. Separability of very noisy mixed

states and implications for NMR quantum computing. _Phys. Rev. Lett._ 83, 1054–1057 (1999). Google Scholar  * Menicucci, N. C. & Caves, C. M. Local realistic model for the dynamics of

bulk-ensemble NMR information processing. _Phys. Rev. Lett._ 88, 167901 (2002). Google Scholar  * Datta, A. & Vidal, G. Role of entanglement and correlations in mixed-state quantum

computation. _Phys. Rev. A_ 75, 042310 (2007). MathSciNet  Google Scholar  * Knill, E. & Laflamme, R. Power of one bit of quantum information. _Phys. Rev. Lett._ 81, 5672–5675 (1998).

Google Scholar  * Biamonte, J. et al. Quantum machine learning. _Nature_ 549, 195–202 (2017). Google Scholar  * Brassard, G. & Hoyer, P. An exact quantum polynomial-time algorithm for

Simon’s problem. In _Proceedings of the Fifth Israeli Symposium on Theory of Computing and Systems_ 12–23 (IEEE, 1997).<q> * Grover, L. K. Quantum computers can search rapidly by using

almost any transformation. _Phys. Rev. Lett._ 80, 4329–4332 (1998). Google Scholar  * Harrow, A. W., Hassidim, A. & Lloyd, S. Quantum algorithm for linear systems of equations. _Phys.

Rev. Lett._ 103, 150502 (2009). MathSciNet  Google Scholar  * Bothwell, J. H. F. & Griffin, J. L. An introduction to biological nuclear magnetic resonance spectroscopy. _Biol. Rev._ 86,

493–510 (2011). Google Scholar  * Hwang, J.-H. & Choi, C. S. Use of in vivo magnetic resonance spectroscopy for studying metabolic diseases. _Exp. Mol. Med._ 47, e139 (2015). Google

Scholar  * Beckonert, O. et al. Metabolic profiling, metabolomic and metabonomic procedures for NMR spectroscopy of urine, plasma, serum and tissue extracts. _Nat. Protoc._ 2, 2692–2703

(2007). Google Scholar  * Larive, C. K., Barding, G. A. & Dinges, M. M. NMR spectroscopy for metabolomics and metabolic profiling. _Anal. Chem._ 87, 133–146 (2015). Google Scholar  *

Napolitano, J. et al. Proton fingerprints portray molecular structures: enhanced description of the 1H NMR spectra of small molecules. _J. Org. Chem._ 78, 9963–9968 (2013). Google Scholar  *

Ravanbakhsh, S. et al. Accurate, fully-automated NMR spectral profiling for metabolomics. _PLoS ONE_ 10, e0124219 (2015). Google Scholar  * De Graaf, A. A. & Boveé, W. M. M. J. Improved

quantification of in vivo 1H NMR spectra by optimization of signal acquisition and processing and by incorporation of prior knowledge into the spectral fitting. _Magn. Reson. Med._ 15,

305–319 (1990). Google Scholar  * Wevers, R. A., Engelke, U. & Heerschap, A. High-resolution 1H-NMR spectroscopy of blood plasma for metabolic studies. _Clin. Chem._ 40, 1245–1250

(1994). Google Scholar  * Wevers, R. A. et al. Standardized method for high-resolution 1H-NMR of cerebrospinal fluid. _Clin. Chem._ 41, 744–751 (1995). Google Scholar  * Govindaraju, V.,

Young, K. & Maudsley, A. A. Proton NMR chemical shifts and coupling constants for brain metabolites. _NMR Biomed._ 13, 129–153 (2000). Google Scholar  * Dashti, H. et al. Applications of

parametrized NMR spin systems of small molecules. _Anal. Chem._ 90, 10646–10649 (2018). Google Scholar  * Dashti, H. et al. Spin system modeling of nuclear magnetic resonance spectra for

applications in metabolomics and small molecule screening. _Anal. Chem._ 89, 12201–12208 (2017). Google Scholar  * Pickard, C. J. & Mauri, F. All-electron magnetic response with

pseudopotentials: NMR chemical shifts. _Phys. Rev. B_ 63, 245101 (2001). Google Scholar  * Paruzzo, F. M. et al. Chemical shifts in molecular solids by machine learning. _Nat. Commun._ 9,

4501 (2018). Google Scholar  * Levitt, M. H. _Spin Dynamics_: _Basics of Nuclear Magnetic Resonance_ (Wiley, 2008). * Dashti, H. Guided Ideographic Spin System Model Optimization

(GISSMO)<q> (2019); http://gissmo.nmrfam.wisc.edu/ * van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. _J. Mach. Learn. Res._ 9, 2579–2605 (2008). MATH  Google Scholar

  * van der Maaten, L. https://lvdmaaten.github.io/tsne/ (2019). * Ester, M., Kriegel, H.-P., Sander, J. & Xu, X. A density-based algorithm for discovering clusters in large spatial

databases with noise. In _Proceedings of the Second International Conference on Knowledge_, _Discovery and Data Mining_ 226–231 (AAAI Press, 1996). * Ulrich, E. L. et al. Biomagresbank.

_Nucleic Acids Res._ 36, D402–D408 (2008). Google Scholar  * Sokolenko, S. et al. Robust 1D NMR lineshape fitting using real and imaginary data in the frequency domain. _J. Magn. Reson._

298, 91–100 (2019). Google Scholar  * Xu, K., Marrelec, G., Bernard, S. & Grimal, Q. Lorentzian-model-based Bayesian analysis for automated estimation of attenuated resonance spectrum.

_IEEE Trans. Signal Process._ 67, 4–16 (2019). MathSciNet  MATH  Google Scholar  * Arute, F. et al. Quantum supremacy using a programmable superconducting processor. _Nature_ 574, 505–510

(2019). Google Scholar  * McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. _Nat. Commun._ 9, 4812

(2018). Google Scholar  * Kokail, C. et al. Self-verifying variational quantum simulation of lattice models. _Nature_ 569, 355–360 (2019). Google Scholar  * Kieferová, M. & Wiebe, N.

Tomography and generative training with quantum Boltzmann machines. _Phys. Rev. A_ 96, 062327 (2017). Google Scholar  * Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B. & Melko, R.

Quantum Boltzmann machine. _Phys. Rev. X_ 8, 021050 (2018). Google Scholar  * Zhou, L., Wang, S.-T., Choi, S., Pichler, H. & Lukin, M. D. Quantum approximate optimization algorithm:

performance, mechanism and implementation on near-term devices. Preprint at https://arxiv.org/abs/1812.01041 (2018). * Radford, N. in _Handbook of Markov Chain Monte Carlo_ (eds Brooks, S.

et al.) 116–162 (CRC, 2011). * Murakami, Y. & Ishihara, S. (eds) _Resonant X-ray Scattering in Correlated Systems_ (Springer, 2017). * Hofstetter, W., Cirac, J. I., Zoller, P., Demler,

E. & Lukin, M. D. High-temperature superfluidity of fermionic atoms in optical lattices. _Phys. Rev. Lett._ 89, 220407 (2002). Google Scholar  * Bloch, I., Dalibard, J. & Zwerger, W.

Many-body physics with ultracold gases. _Rev. Mod. Phys._ 80, 885–964 (2008). Google Scholar  * Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J.

Resonant inelastic X-ray scattering studies of elementary excitations. _Rev. Mod. Phys._ 83, 705–767 (2011). Google Scholar  * Kreula, J. M. et al. Few-qubit quantum-classical simulation of

strongly correlated lattice fermions. _EPJ Quantum Technol._ 3, 11 (2016). Google Scholar  Download references ACKNOWLEDGEMENTS D.S. acknowledges support from the FWO as post-doctoral fellow

of the Research Foundation—Flanders and from a 2019 grant from the Harvard Quantum Initiative Seed Funding programme. S.M. is supported by a research grant from the National Heart, Lung,

and Blood Institute (K24 HL136852). O.D. and H.D. are supported by a research award from the National Heart, Lung, and Blood Institute, (5K01HL135342) and (T32 HL007575) respectively. E.D.

acknowledges support from the Harvard–MIT CUA, ARO grant number W911NF-20-1-0163, the National Science Foundation through grant number OAC-1934714, AFOSR Quantum Simulation MURI.The authors

acknowledge useful discussions with P. Mehta and M. Lukin. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Harvard University, Cambridge, MA, USA Dries Sels & Eugene

Demler * Theory of Quantum and Complex Systems, Universiteit Antwerpen, Antwerpen, Belgium Dries Sels * Division of Preventive Medicine, Brigham and Women’s Hospital, Harvard Medical

School, Boston, MA, USA Hesam Dashti, Samia Mora & Olga Demler * Division of Cardiovascular Medicine, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA Samia Mora

Authors * Dries Sels View author publications You can also search for this author inPubMed Google Scholar * Hesam Dashti View author publications You can also search for this author inPubMed

 Google Scholar * Samia Mora View author publications You can also search for this author inPubMed Google Scholar * Olga Demler View author publications You can also search for this author

inPubMed Google Scholar * Eugene Demler View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.S. and E.D. conceived the presented idea in

consultation with H.D., S.M. and O.D. D.S. developed the theoretical formalism, performed the analytic calculations and performed the numerical simulations. H.D. compiled the NMR data used

in the manuscript. All authors provided critical feedback and helped shape the manuscript. CORRESPONDING AUTHOR Correspondence to Dries Sels. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Discussion and Figs. 1–5. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE

Sels, D., Dashti, H., Mora, S. _et al._ Quantum approximate Bayesian computation for NMR model inference. _Nat Mach Intell_ 2, 396–402 (2020). https://doi.org/10.1038/s42256-020-0198-x

Download citation * Received: 17 September 2019 * Accepted: 02 June 2020 * Published: 06 July 2020 * Issue Date: July 2020 * DOI: https://doi.org/10.1038/s42256-020-0198-x SHARE THIS ARTICLE

Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative