Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond

Whenever a quantum system undergoes a cyclic evolution governed by a slow change of parameters, it acquires a phase factor: the geometric phase. Its most common formulations are known as the

Aharonov–Bohm phase and the Pancharatnam and Berry phase, but both earlier and later manifestations exist. Although traditionally attributed to the foundations of quantum mechanics, the

geometric phase has been generalized and become increasingly influential in many areas from condensed-matter physics and optics to high-energy and particle physics and from fluid mechanics

to gravity and cosmology. Interestingly, the geometric phase also offers unique opportunities for quantum information and computation. In this Review, we first introduce the Aharonov–Bohm

effect as an important realization of the geometric phase. Then, we discuss in detail the broader meaning, consequences and realizations of the geometric phase, emphasizing the most

important mathematical methods and experimental techniques used in the study of the geometric phase, in particular those related to recent works in optics and condensed-matter physics.

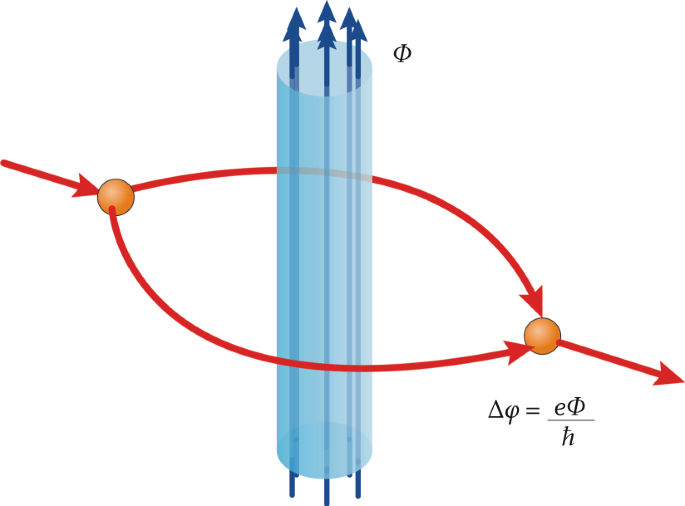
The Aharonov–Bohm phase, acquired by charged particles encircling a confined magnetic flux, is topological, gauge invariant and realistic, highlighting the unique role of electromagnetic

potentials in quantum mechanics.

The Aharonov–Bohm phase can be seen as a manifestation of Berry’s geometric phase accumulated whenever a quantum system is adiabatically transported around a cyclic circuit on an abstract

surface in the parameter space (with additional generalizations to degenerate and open systems, and to non-adiabatic, non-cyclic, non-unitary evolutions).

The geometric phase is an example of a holonomy (failure of parallel transport around closed cycles to preserve the geometrical information being transported) and its profound role in

physics.

The two main types of geometric phase in optics originate from ‘spin redirection’ (when light with a fixed state of polarization is changing direction) and from a slow change in polarization

(of light propagating through an anisotropic medium in a fixed direction), giving rise to the Pancharatnam–Berry phase.

In condensed-matter physics, the geometric phase manifests itself in the electronic Bloch states, quantum Hall effect, electric polarization, exchange statistics and many other phenomena.

This work was supported by Canada Research Chair (CRC), Canada Foundation for Innovation (CFI), Canada First Excellence Research Fund (CFREF) Program, DFG grants no. MI 658/10-1, no. RO

2247/8-1 and CRC 183, Leverhulme Trust and the Italia-Israel project QUANTRA.

Department of Physics, University of Ottawa, Ottawa, Ontario, Canada

Eliahu Cohen, Hugo Larocque, Frédéric Bouchard, Farshad Nejadsattari & Ebrahim Karimi

Faculty of Engineering and Institute of Nanotechnology and Advanced Materials, Bar Ilan University, Ramat Gan, Israel

Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, Israel

All authors have read, discussed and contributed to the writing of the manuscript.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Any properties of a topological space that are invariant under homeomorphisms.

The number of times that a closed curve travels anticlockwise around a point on a surface.

Operation that allows parallel transport over the vector bundle.

A certain topological invariant associated with vector bundles on smooth manifolds.

The quantum analogue of classical random walk taking advantage of quantum coherent superposition.

Anyone you share the following link with will be able to read this content: