Immobility of isolated swarmer cells due to local liquid depletion

ABSTRACT Bacterial swarming is a complex phenomenon in which thousands of self-propelled rod-shaped cells move coherently on surfaces, providing a highly studied example of active matter.

However, bacterial swarming is different from most studied examples of active systems because single isolated cells do not move, while clusters do. The biophysical aspects underlying this

behavior are unclear. In this work we explore the case of low local cell densities, where single cells become temporarily immobile. We show that immobility is related to local depletion of

liquid. In addition, it is also associated with the state of the flagella. Specifically, the flagellar bundles at (temporarily) liquid-depleted regions are completely spread-out. Our results

suggest that dry models of self-propelled agents, which only consider steric alignments and neglect hydrodynamic and hydration effects, are oversimplified and are not sufficient to describe

swarming bacteria. SIMILAR CONTENT BEING VIEWED BY OTHERS BACTERIA SOLVE THE PROBLEM OF CROWDING BY MOVING SLOWLY Article 23 November 2020 COLLECTIVE CONDENSATION AND AUTO-AGGREGATION OF

_ESCHERICHIA COLI_ IN UNIFORM ACIDIC ENVIRONMENTS Article Open access 21 August 2024 SELF-ORGANISATION AND CONVECTION OF CONFINED MAGNETOTACTIC BACTERIA Article Open access 11 August 2020

INTRODUCTION Bacterial swarming is a collective mode of motion in which rod-shaped cells, powered by multiple flagella, move and migrate on surfaces by forming dynamic clusters that

continually split and merge1,2,3,4,5,6,7,8,9,10,11,12,13. The clusters have the structure of whirls and jets that are visually reminiscent of collective motion patterns such as seen in

flocks of birds and schools of fish14. However, for bacteria, swarming is more than a collective movement pattern or dynamical phase, but a biological state, termed “lifestyle”. Bacterial

swarming has been described as a particular phenotype, in the sense that swarmers show a significant increase in the expression of some swarming-related genes, even in species that are

described as swarmers but are powered by motive organelles that are not flagella1,15. Swarming as a phenomenon is not species specific, although the cell shape in the colony, typical speeds,

densities and the thickness of colonies depend on the species and the environment16. The evolutionary advantage of swarming is not completely understood, but swarmers are more resistant to

antibiotic stress17,18,19,20 and to a variety of adverse environmental conditions21,22. In addition, it has been hypothesized that foraging by swarmers is more efficient compared to

swimmers23. Physically, bacteria live at low Reynolds numbers where viscous forces dominate24,25,26,27,28,29,30,31,32. In order to overcome viscosity and the friction between the cell and

the surface, swarming bacteria secrete osmotic agents to extract water from the surface33,34, as well as surfactants or lubricants2,21,35,36. Thus, it is thought that the cells inhabit a

thin layer of liquid, a few micrometers thick, in which they eventually move. The collective cellular motion obtained during bacterial swarming has been attributed to steric alignment

(mainly due to excluded volume), and to hydrodynamic interactions. Swarming is different from swimming (in bulk liquid) in many physical aspects including cell aspect ratio37,38, the

mechanism for propulsion39,40 and the quasi two-dimensional topology of swarm colonies41. The dynamics of both swimming and swarming bacteria have been analyzed extensively using the tools

of statistical physics12,24,26,30,31,32,42,43. For example, spatial and temporal correlation functions have been used, both in simulations and experiments, to infer putative phase diagrams,

describing qualitatively distinct dynamical regimes8,27,28,44. One of the prominent differences between swimmers and swarmers is their behavior at low densities. Isolated swimming cells move

at relatively high speeds, of the order of 10 μm/s30,31,32. In this respect, the behavior of large populations of bacterial swimmers is similar to other examples of active systems, such as

larger animals (e.g., birds, fish14), synthetic material (e.g., Janus particles, Quincke rollers or hexbugs45,46,47) and most simulations of self-propelled agents48,49,50. In contrast, most

isolated swarming cells do not move29 and speed increase with density (up to very high densities8,12,28,51,52,53). At low to intermediate densities, this leads to another phase in which

large, dense moving clusters are surrounded by scattered stationary cells51. The physical mechanisms underlying the inability of isolated cells to move are currently unknown and are the main

focus of this manuscript. Previous works54,55 speculated that the absence of motion at low densities may depend on the lack of physical contact between cells, or the local absence of moist

or water, suggesting that solitary individuals are unable to overcome the frictional forces between the cell and the surface. RESULTS EXPERIMENTAL SETUP We work with _Bacillus subtilis_

(wild-type 3610; labeled red, strain AE4847 amyE::Pveg_R0_mKate;specR), which is a model swarm species that has been used extensively in the past2,10. The cells, which are rod-shaped (1 × 7 

μm), are grown in Petri-dishes under standard swarm conditions (0.5% agar and 25 g/l LB; incubated at 30 °C, 95% relative humidity (RH)). Prior to inoculation, the plates are aged for 24 h

in the lab (24 °C and 30% RH) with the lid on, and then are opened for 8 more minutes to remove extra moisture. Moisture is removed to allow proper absorption of the 5-μl drop of log-phase

liquid culture by the agar. Starting from a small spot at the center of the colony, with ~5 × 105 cells, the colony grows and expands rapidly outwards; we focus on the outer regions of the

colony near its edge where the averaged surface fraction _ρ_ covered by cells is _ρ_ = 0.3. Optical microscopy was used to track the location of the cells as a function of time, from which

we generate all the data (Zeiss Axio Imager Z2 at 63× with phase-contrast, brightfield and fluorescence (filter set 20 Rhodamin shift free: Excitation 546/12; Beam Splitter 560; Emission

607/80) modes, hooked to a Neo (Andor) camera operated at 1000 × 1000 pixels and up to 50 frames/s. In addition, we use differential interference contrast (DIC) microscopy, which enables,

among other things, the detection of surface roughness by showing different colors for different slopes in the sample (see Methods section for more details). We use a Zeiss Axioscope 5 at

63× to which we have added an additional Rochon prism in some of the experiments. The microscope is hooked to a color Axiocam 208 camera operated at 1000 × 1000 pixels with still images

taken at 0.02 s exposure and video with a frame rate of 30 frames/s. See the Methods section for details on staining the flagella and image analysis. MAIN RESULTS Figure 1a, b show an

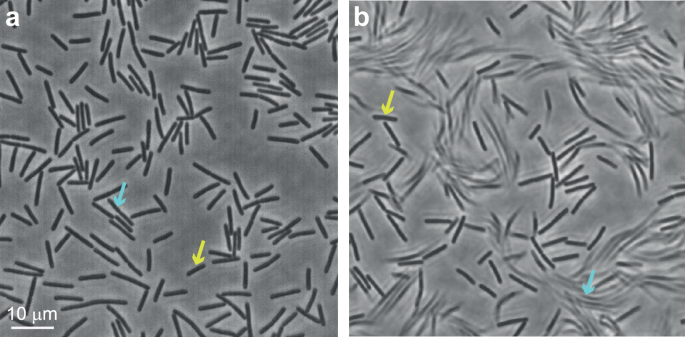
example of the region of interest, with the cells seen on the agar, for two different exposure times (phase-contrast). At high frame rate (50 frames/s; exposure time = 0.02 s), all the cells

(_ρ_ = 0.3) are clearly seen (Fig. 1a), but at a slower rate (5 frames/s; exposure time = 0.2 s) only the cells that are temporarily immobile are seen (Fig. 1b), while the moving ones are

smeared. By thresholding the image, the fraction of immobile cells is determined. To understand why some cells are _temporarily_ immobile, we first checked whether the agar is smooth and

uniform, as perhaps there are regions that tend to trap, or un-trap cells. The field of view is thus divided into 100 equally sized bins (10 × 10), and the fraction of time each bin is

inhabited with an immobile cell is measured for all bins (at least 1/3 the size of a cell in a bin is needed to count one). We repeat this measurement for a variety of durations, from 5 s to

360 s in steps of 5 s. Our results show (Fig. 2a) that on average, each bin is occupied with immobile cells about 6% of the time. This result does not depend on the duration. We also look

at the distribution among the 100 bins and obtain that the occupation counts are Gaussian. The standard deviation (Fig. 2a inset) decreases as _t_-1/2 indicating that the stagnation of cells

is a sum of independent events. Additionally, we calculate the time correlation function, which quantifies how long the fluctuations with respect to the average occupation of 6% are

maintained over time. We observe that the correlation drops to zero after just a few seconds (Fig. 2b). These results suggest that there are no fixed locations that tend to trap or un-trap

the cells (Fig. 2c, d). In other words, over time, the surface is homogeneous. In Fig. 2e–h we show results for the same experiment, only that now we have dried the agar plates for 4 times

longer prior to inoculation, making the surface less wet. The results show that the number of stationary cells at a given time is larger, as the average inhabitation of bins by the immobile

cells is 13% of the time. As in wetter conditions, the distribution remains Gaussian and the time correlation drops to zero, suggesting that the lack of liquid does not create fixed local

traps. Overall, the results suggest that there are wet points of tiny “ponds” but those are not fixed in time and space. Figure 3a shows results for the distribution of speeds in the two

(wet and dry) cases (data was taken at 50 frames/s). We suggest that the drying time affects mostly the stationary, and the slowly moving cells (e.g., cells that move slower than 7 μm/s).

Clearly, the number of non-moving cells is larger at the dry case; however, the cells that are moving faster than 7 μm/s (i.e., cells that were not affected by the lack of water) exhibit the

same average speed (19.5 μm/s for the wet case and 18.6 μm/s for the dry case), and a similar speed distribution (Fig. 3b). As in past studies, the speed distribution has a Gaussian tail as

expected for the Rayleigh distribution (e.g.,20). Next, we show that immobile cells are isolated, in the sense that they are not close to other cells. Figure 3c, d, show the average speed

as a function of the number of neighbours up to a cut-off distance. We see that ells that are isolated are completely stationary. Above a critical number of cells, the speed increases

linearly up to about 20 µm/s. In Fig. 4 we compare results obtained under different illumination techniques. At a large enough frame rate (50 frames/s), when the cells are not smeared due to

their motion, the fluorescence mode, the bright-field and the phase-contrast, all show that both the stationary cells and the moving ones exhibit a similar intensity, where it is impossible

to tell by a single snapshot which cells are stationary, and which ones are moving. However, the DIC image shows that stationary cells and moving ones have a different color (Fig. 4d). In

DIC the color (e.g., the hue of the color obtained in the HSB color system), indicates a slope in the surface of the sample with respect to the parallel microscope table (i.e., perpendicular

to the beam)56. The same hue is obtained for regions in the agar that are free of cells, and for the moving cells. This suggests that the local surface of the moving cells is parallel to

the agar, presumably due to the presence of a thin liquid layer on top of them, causing the cells not to be easily resolved. However, stationary cells are nicely resolved, and their hue

reflects the slopes of their rod-shaped structure. To increase the DIC hue-contrast even more (Fig. 5a), we have added an _additional_ Rochon prism to the DIC system, and then threshold the

image by the hue (we “label” all pixels with hue equal or smaller than 20 in black, in between 21–24 blue, and 25–27 in green, while the agar background, as well as the moving cells are

typically in the range of 43-45). Also, there are very few pixels in the entire field of view in the range of 28–42 so that the moving cells and the stationary ones are clearly distinguished

(Fig. 5b). Figure 5c–g show the gradual stopping process of a single cell. Figure 5c shows a moving cell, that then stops (Fig. 5d), and starts losing the liquid around it (Fig. 5e–g), with

more regions of the cell appear to be blue and black, indicating the loss of the liquid that was covering it. Figure 5h–l show the gradual acceleration of a single cell (from stationary to

moving). Figure 5h–j show a stationary cell that gets wetter as the blue and black colors disappear. In the next frame (Fig. 5k), the cell is not moving yet. It eventually accelerates (Fig. 

5l) as enough of the liquid covers it. Additional results (Supplementary Movie S1 and Supplementary Movie S2) show tiny ( ~ 0.5 μm in diameter) MgO beads deposited on the colony (See methods

in Refs. 35,57). While beads on the virgin agar are immobile (Supplementary Movie S1), those near stationary cells (Supplementary Movie S2) do move, indicating the presence of liquid

streams that are sufficient to drag the beads but not the cells. This establishes that liquid flow around a cell is not sufficient to move it. Next, we study the flagellar arrangement using

fluorescence staining of the live bacteria (see the Methods section for details). The results show that swarming cells may be largely divided into three categories (Supplementary Movie S3).

This classification is independent of the drying time. (i) Closed (Fig. 6a); with all flagella tightly wrapped around one of the poles, (ii) (Fig. 6b) Partially open; with flagella partially

unbundled, and (iii) (Fig. 6c) Open; where the flagella are completely unbundled, but are still rotating. Analyzing the trajectories of the cells, the state of the flagella is labeled

manually. We obtain the probability distribution of two characteristics for each of the categories. In Fig. 6d we show the distribution of speeds for the wet case (the drier case is

_qualitatively_ similar). Cells with completely unbundled (open) flagella (data in red) are almost never moving, while cells of the two other states do move, but with different speed

distributions (inset of Fig. 6d). We also show the time durations the cells spend in each state (Fig. 6e). The data of the stationary cells is compared to the data taken from the DIC

experiments with a fair similarity. We refer to the closed flagella state as “run”, to the partially open (partially unbundled) state “tumble”, because cells change their direction of motion

and do not move in straight lines, and to the open flagella “stall”. Lastly, we establish that the transition between the three flagellar states is statistically consistent with a

continuous time Markov chain. Figure 6f shows the histogram of the waiting times in the closed and partially open states on a semi-log plot along with the maximum likelihood fit to an

exponential distribution. The fit, with averages 0.25 s and 0.21 s, respectively, is very good. Fitting the duration of the closed state (Fig. 6g) to an exponential distribution (average

0.95 s), is not as good. Fitting to a mixture of two exponential distribution is better, but is not statistically justified AIC of a single exponential – AIC of mixture = -2.5). Thus, within

the data available, the approximation to an exponential waiting time is justified. Figure 6h shows the transition matrix between the states. No events of shifting directly from closed (run)

to open (stall) or vice versa were observed ( > 1000 measurements). The transition from the partial (tumble) state to run or tumble are close to equal. In order to see if these

transitions are memoryless, we compare the two-step transition matrix (Fig. 6i) with the square of the single step one (Fig. 6j). The two are equal up to a relative error of ~1%. Overall, we

conclude that the transition dynamics between the states is consistent with a memoryless (continuous time) Markov chain whose transition probabilities are found in Fig. 6h and transition

rates out of the closed, partial and open states are 4, 4.76 and 1.05 1/s, respectively. DISCUSSION It is well known that moisture is a prerequisite for swarming in all bacterial species.

This understanding, which has been noted since the first, pioneering works on bacterial swarming7,55,58 concerns the overall environment of the colony. In other words, it is a global

requirement. In the current work, we address the spatial and temporal local conditions for cell movement within a swarm. We showed that while clusters of cells migrate rapidly on the agar,

cells in the swarming state with no close neighbors do not move until they are covered with enough liquid. Our results show that the overall availability of water plays a significant role in

determining the fraction of temporarily immobile cells among a population, and the duration each of these cells will be stationary. We also see that cells that were not trapped by the local

depletion of liquids are not affected and will move with similar statistics, regardless of the overall availability of the water. In addition, we show that flagellar arrangement is strongly

correlated with the cellular motion, which is also strongly correlated with the local presence of liquid around the cell. Cells that are temporarily left alone are immobile, are not covered

with enough liquids, and have their flagella widely open. Cells in a cluster are mobile, are covered with liquid, and have their flagella arranged in a bundle. With that, our results cannot

conclude on what is the cause and what is the effect. The transitions between the flagellar states are consistent with a continuous time Markov chain. Previous works showed that during

swarming, the chemotaxis mechanism is suppressed17,59. However, cells do change direction through spontaneous clockwise flagellar rotations. This is true even in cheB mutants (_B. subtilis_

strain DS90) that are locked in the counter clockwise direction and are constantly in a run-only phase when in liquid bulk (but not on agar)39,59. Thus, the complete opening of the flagella

while stalling is not necessarily related to chemotactic behavior. These dynamics are similar to previously reported observations by Turner et al.60, who noted that _Escherichia coli_ swarm

cells follow four kinds of tracks (modes) that strongly depend on the flagellar arrangement: stalls, reversals (not studied here), lateral movement, and forward movement. The “stall” mode,

which is similar to the one reported here, was mostly found in cells that are at the edge of the colony. Moreover, these cells have their flagella completely spread out, pointing outward60.

They speculated that this is a mechanism for extracting or pumping water from the substrate, thus moving the colony edge forward. Our results on _B. subtilis_ show that the completely open

flagella state is also observed inside the active swarm among solitary cells that have a temporal depletion of liquid around them. This suggests that the “stall” state may be related to a

cellular mechanism for extracting liquid. Overall, we showed that moisture and the local amount of liquid around cells play a pivotal role in understanding the biophysics underling the

bacterial swarming phenomenon. Specifically, dry models of self-propelled agents, which only consider steric alignments and neglect hydrodynamic interactions and the local amount of liquids,

are oversimplified and are not sufficient to describe swarming bacteria. METHODS TL DIC MICROSCOPY In the current work we use Transmitted-Light Differential Interference Contrast (TL DIC)

microscopy equipped with color “enhancement”. As in all color-DIC systems, the incident light travels through a polarizer, a Rochon/Wollaston/Nomarski prism that splits the ray, and a lambda

plate. In our case, the light hits the sample from below, the bottom side of the sample is flat and smooth, and the substrate does not have birefringent properties (the bottom of the

Petri-dish is made of a special glass and not the standard plastic). Loosely speaking, the color-DIC system can differentiate between slopes in the sample, which are manifested in the hue

property of colors. Differences in the index of refraction between the cells and the water (liquid), which are typically smaller than 0.05, do not play a role in determining the obtained

hue, specifically in our systems where the cells are thin; Within the tested range, the same hue will be obtained for all objects in the sample if they have the same slope. In non-color DIC

for instance, the differences in the index of refraction are resulted in an almost complete destructive interference, and only the perimeter of the cells may be resolved. This means that in

color-DIC, cells embedded in water are almost invisible (in contrast e.g., to phase-contrast microscopy where cells embedded in water are nicely resolved). Overall, within the experimental

conditions and range of the slopes measured, the obtained hue is a monotonic function of only the local slopes in the upper surface and not of the material through which the light is

transmitted. Mind that the saturation and luminance do depend on the material (its thickness or density for instance) through which the light is transmitted so the cells may sometimes be

seen e.g., in Fig. 4c. The lateral resolution (in the viewing plane) of DIC is of the order of the wavelength i.e., ~0.5 μm (stemming from the 0.2 μm adjutant points of the two split rays),

and the ability to resolve the vertical axis by the hue is typically of the order of 0.05 μm, which yields an approximate minimal “local” angle of detection of ~4° (i.e., slopes smaller than

4° are not easily resolved; there is also a maximal angle above which the light is reflected away from the lens and the sample becomes dark). In order to relate between the liquid around a

cell and the measured hue value, consider a cross section of a bacterium with a cylindrical shape with a diameter 1 μm, resting on a flat surface (see Fig. 7a). Liquid (e.g., water) may

cover the cell completely or partially. In Fig. 7b, the cell is completely covered. The height of the water is not important – only the angle it creates with respect to the tangent to the

“ridge” of the cell. Thus, all samples that are covered by a flat-water interface will yield the same hue, regardless of the water height. In Fig. 7c we show a different case where the

liquid does not completely cover the cell, resulting in different interfacial slopes around the cell. The ridge of the cell is parallel to the background and will yield the same hue.

However, the edges of the cell are covered with liquid that creates a changing slope; the local slope will yield a hue that reflects the slope’s value. In Fig. 7d-e, the layer of liquid is

shallow, or there is no liquid at all. In these cases, only the ridge of the cell has a parallel surface that will yield the same hue as the one seen for the background. The edges of the

cell will have different hues depending on their local slopes, independently of the liquid. Upon increasing the liquid layer, the system transitions from Fig. 7d, e to Fig. 7c or even Fig. 

7b, and the slopes of the liquid on the cell edges become moderate, which changes the hue to the background value. Note that the ridge of the cell is very narrow; it is narrower than the

lateral resolution – therefore, the background hue is seldom obtained on the ridge. To illustrate how DIC works on transparent objects embedded in transparent medium, we performed an

experiment described next and documented in Fig. 8. In Fig. 8a we show a set of 10 images of spherical silica beads (the larger ones are 5 μm in diameter) deposited on an agar surface. A

drop of water, mixed with surfactant, is allowed to spread over the agar. The surfactant is added to form a relatively thin liquid front. The phase-contrast images are presented in order to

show the advancing edge of the drop that covers the beads (from left to right). The images show that the beads are nicely resolved with, and without the water on top of them, and that they

are not being flashed by the liquid (they are slightly embedded in the agar and a slight motion might be detected as the agar is rewetted). The 10th image shows the agar after the focus was

readjusted manually. The DIC set of 10 images (Fig. 8b), shows a silica bead and the different colors (hues) that are exhibited along a diagonal line parallel to the beam splitting direction

(from top-left to bottom-right). The hues reflect the structure of both the bead and the surface on which it is deposited. The top of the bead has the same hue as the one seen at the

background (pale-blue). At t = 0 s, the intensity of the outer regions of the bead are low due to the relatively large angles, as most light is reflected away from the objective lens. The

reddish and yellowish colors along the beam splitting direction, but outside of the bead, indicate that the bead is slightly embedded in the agar. When water approaches (from top right to

bottom left), the bead is completely covered with water, and the surface becomes flat and smooth and almost parallel to the agar (except for the advancing contact angle which is very small ~

7° (at t = 10 s); it thus appears brown and not pale-blue). In contrast to the phase-contrast case, in the DIC images the bead is completely invisible – even though we travel with the stage

to find the appropriate focus. After a few minutes (the process is gradual but may be fairly seen after few minutes), the surface becomes pale-blue again because the angle of the drop

decreases. The experiment lasts about 20 min during which the water evaporates and absorbed by the agar (and the bead drifts a bit with respect to the lab because the soft agar is not stable

enough during the “flood”). During capturing, we play with the focus every few seconds to verify that the bead cannot be detected. The bead sometimes appears as a pale ring with a dot at

its center, but only when the water level is low enough, the colors reappear. FLAGELLA STAINING Our protocol is similar to other protocols recently used to stain flagellar filaments in

_Bacillus subtilis_ 3610 and other species60,61; yet, in our case the cells are swarmers. In the strain we have used (DS1916, amyE::Phag-hagT209C spec), the flagellin protein genes have been

modified to include the cysteine amino acid that binds to the maleimide functional group62, allowing staining using Alexa 546 dye (ThermoFischer ref A10258). Bacteria are grown overnight ( 

~ 18 h) in 2 ml of LB (25 g/l), at 30 °C and shaking (200 rpm), from which 10 µl is used to inoculate three swarm plates (LB with 0.5% agar). When the droplets dry out, the plates are placed

in an incubator at 30 °C with controlled high humidity ( ~ 95% RH). Additionally, a fourth plate is inoculated with a one-hour delay. This plate will be used to reincorporate the stained

bacteria into swarming conditions. To facilitate that process, the inoculation is done slightly off-center. The remaining overnight culture is centrifuged for 3 min at 2000 g, and the

supernatant is saved for later. The three initial plates are incubated for 5 h, after which the bacteria are collected by flushing the colonial edge with phosphate buffer (0.01 M ph~7.2) and

then collecting the liquid with the cells. Special attention must be put into collecting bacteria exclusively from the edge, where bacteria are in the swarming state. If not, bio-aggregates

are created by bacteria in the biofilm, disturbing the following steps. After collection, flagella are stained by adding 5 μl of the dye solution (20 μg/μl of Alexa 546 in DMSO). We allow

staining to occur for one hour while the suspension is rotated at 100 rpm to prevent bacterial sedimentation. Then, bacteria are centrifuged for 3 min at 2000g and resuspended in the

overnight supernatant (0.2 μm filtered). Then, 20 μl is inoculated into the fourth agar plate. The inoculation drop is introduced outside of the colony, and then it spreads along the

boundary of the colony, forming an arc, never being in direct contact with the colony. After drying, the plate is replaced in the incubator for 30 min or until the colony integrates with the

stained bacteria. At the end of this process, one will obtain a swarming colony where a fraction of the cells has stained flagella. Observation was done using the same fluorescence setup

described above (Zeiss Axio Imager Z2 at 63×, filter set 20 Rhodamin shift free: Excitation 546/12; Beam Splitter 560; Emission 607/80), and a Zyla Andor operated at 100 frames per second.

IMAGE ANALYSIS The quantitative analysis presented in Figs. 2 and 3 is facilitated using custom image analysis software implemented in Matlab. First, images undergo standard smoothing and

preprocessing, as detailed in Ref. 40. Applying a threshold on the intensity yields a Boolean mask indicating whether each pixel corresponds to a cell or not. Occupancy statistics (Fig. 2)

corresponds to pixel-wise counts (and not number of cells). The sequence of images is used to obtain velocity field using optical flow analysis (see30 for details). Such algorithms

inherently involve smoothing. Average speeds (Figs. 3a, b) are obtained directly from the vector fields without taking into account speeds below a threshold. In other words, we average only

over pixels that correspond to moving objects. The implementation follows40. Figure 3c, d show the average speed of cells as a function of the number of neighbors (up to a given distance).

This requires identifying the position of individual cells and therefore tracking of individuals. To this end, we apply a method for tracking elongated objects using the Hough transform.

First, the Boolean mask is separated into connected blobs using standard image analysis tools in Matlab. Blobs that are too small (in area or length) are discarded. The main difficulty is

that cells that are practically touching are often associated with the same blob. To bypass this problem, in each blob, we find the longest line segment using the Hough transform. This

segment (with some added thickness) is removed from the blob. Segments that are longer than 1.5 the average cell length are split in two. Repeating the process, we obtain a list of line

segments that correspond to the individual cells. Once individual cells were identified as line segments, we need to associate cells in consecutive frames to obtain trajectories. Typically,

tracking software use the central points to find which cell in one image is closest to which cells in the following one. Here, we use the sum of the distances between the endpoints, which

also takes into account the orientation and length of the detected cells. Since the order of the endpoints in each line segment is arbitrary, one needs to take the minimum between two

ordering options. We perform a standard greedy pair matching algorithm, starting at the closed pair up to a cutoff distance of about 3 average cell lengths. Next, the endpoints of each

trajectory are smoothed over time using malowess with a linear interpolation. Velocities of the center of mass can then be calculated. Finally, to calculate the number of neighbors a focal

cell has up to a given distance, we find the average number of endpoints associated with other cells to each of the endpoints of the focal cell. In other words, instead of counting cells, we

count endpoints, each “worth” half a cell. This counting is used to calculate the statistics in Fig. 3c, d. REPORTING SUMMARY Further information on research design is available in the 

Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY All data will be available upon request. REFERENCES * Harshey, R. M. Bees aren’t the only ones: swarming in

Gram‐negative bacteria. _Mol. Microbiol._ 13, 389–394 (1994). Article  Google Scholar  * Kearns, D. B. A field guide to bacterial swarming motility. _Nat. Rev. Microbiol._ 8, 634–644 (2010).

Article  MATH  Google Scholar  * Hefetz, I. et al. A reversible mutation in a genomic hotspot saves bacterial swarms from extinction. _iScience_ 26, 106043 (2023). Article  ADS  MATH 

Google Scholar  * Li, H., Chaté, H., Sano, M., Shi, X. Q. & Zhang, H. P. Robust Edge Flows in Swarming Bacterial Colonies. _Phys. Rev. X_ 14, 1–15 (2024). ADS  Google Scholar  * Anda, J.

D. et al. collectively swarm. 15, (2024). * Harshey, R. M. Bacterial Motility on a Surface: Many Ways to a Common Goal. _Annu. Rev. Microbiol._ 57, 249–273 (2003). Article  Google Scholar 

* Damton, N. C., Turner, L., Rojevsky, S. & Berg, H. C. Dynamics of bacterial swarming. _Biophys. J._ 98, 2082–2090 (2010). Article  ADS  Google Scholar  * Jeckel, H. et al. Learning the

space-time phase diagram of bacterial swarm expansion. _Proc. Natl. Acad. Sci. USA_ 116, 1489–1494 (2019). Article  ADS  MATH  Google Scholar  * Copeland, M. F. & Weibel, D. B.

Bacterial swarming: a model system for studying dynamic self-assembly. _Soft Matter_ 5, 1174–1187 (2009). Article  ADS  MATH  Google Scholar  * Kearns, D. B. & Losick, R. Swarming

motility in undomesticated Bacillus subtilis. _Mol. Microbiol._ 49, 581–590 (2003). Article  Google Scholar  * Partridge, J. D. Surveying a Swarm: Experimental Techniques To Establish and

Examine Bacterial Collective Motion. _Appl. Environ. Microbiol_. 88, (2022). * Be’er, A. & Ariel, G. A statistical physics view of swarming bacteria. _Mov. Ecol._ 7, 1–17 (2019). Article

  MATH  Google Scholar  * Anyan, M. E. et al. Type IV pili interactions promote intercellular association and moderate swarming of Pseudomonas aeruginosa. _Proc. Natl. Acad. Sci. USA._ 111,

18013–18018 (2014). Article  ADS  Google Scholar  * Vicsek, T. & Zafeiris, A. Collective motion. _Phys. Rep._ 517, 71–140 (2012). Article  ADS  MATH  Google Scholar  * Kaiser, D.

Bacterial Swarming: A Re-examination of Cell-Movement Patterns. _Curr. Biol._ 17, 561–570 (2007). Article  MATH  Google Scholar  * Srinivasan, S., Nadir Kaplan, C. & Mahadevan, L. A

multiphase theory for spreading microbial swarms and films. _Elife_ 8, 1–28 (2019). Article  MATH  Google Scholar  * Partridge, J. D., Ariel, G., Schvartz, O., Harshey, R. M. & Be’er, A.

The 3D architecture of a bacterial swarm has implications for antibiotic tolerance. _Sci. Rep._ 8, 1–11 (2018). Article  Google Scholar  * Butler, M. T., Wang, Q. & Harshey, R. M. Cell

density and mobility protect swarming bacteria against antibiotics. _Proc. Natl. Acad. Sci. USA._ 107, 3776–3781 (2010). Article  ADS  MATH  Google Scholar  * Walker, D. M. Dead cells

release a ‘necrosignal’ that activates antibiotic survival pathways in bacterial swarms. _Nat. Commun_. 1–12 https://doi.org/10.1038/s41467-020-17709-0. * Benisty, S., Ben-Jacob, E., Ariel,

G. & Be’er, A. Antibiotic-induced anomalous statistics of collective bacterial swarming. _Phys. Rev. Lett._ 114, 1–5 (2015). Article  MATH  Google Scholar  * Be’er, A. et al.

Paenibacillus dendritiformis bacterial colony growth depends on surfactant but not on bacterial motion. _J. Bacteriol._ 191, 5758–5764 (2009). Article  MATH  Google Scholar  * Grobas, I.,

Polin, M. & Asally, M. Swarming bacteria undergo localized dynamic phase transition to form stress-induced biofilms. _Elife_ 10, 1–22 (2021). Article  Google Scholar  * Ariel, G. et al.

Swarming bacteria migrate by Lévy Walk. _Nat. Commun_. 6, (2015). * Aranson, I. S. Bacterial active matter. _Reports Prog. Phys_. 85, (2022). * Purcell, E. M. & Purcell Pdf. _American

Journal Physics_ 45, 3–11 (1977). Article  ADS  Google Scholar  * Elgeti, J., Winkler, R. G. & Gompper, G. Physics of microswimmers - Single particle motion and collective behavior: A

review. _Reports Prog. Phys_. 78, (2015). * Wensink, H. H. et al. Meso-scale turbulence in living fluids. _Proc. Natl. Acad. Sci. USA_ 109, 14308–14313 (2012). Article  ADS  MATH  Google

Scholar  * Be’er, A. et al. A phase diagram for bacterial swarming. _Commun. Phys._ 3, 1–8 (2020). Article  Google Scholar  * Zhang, H. P., Be’er, A., Florin, E.-L. & Swinney, H. L.

Collective motion and density fluctuations in bacterial colonies. _Proc. Natl. Acad. Sci. USA_ 107, 13626–13630 (2010). Article  ADS  Google Scholar  * Sokolov, A. & Aranson, I. S.

Reduction of viscosity in suspension of swimming bacteria. _Phys. Rev. Lett._ 103, 2–5 (2009). Article  MATH  Google Scholar  * Sokolov, A. & Aranson, I. S. Physical properties of

collective motion in suspensions of bacteria. _Phys. Rev. Lett._ 109, 1–5 (2012). Article  MATH  Google Scholar  * López, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clément, E.

Turning Bacteria Suspensions into Superfluids. _Phys. Rev. Lett._ 115, 1–5 (2015). Article  MATH  Google Scholar  * Chen, B. G., Turner, L. & Berg, H. C. The wetting agent required for

swarming in Salmonella enterica serovar typhimurium is not a surfactant. _J. Bacteriol._ 189, 8750–8753 (2007). Article  Google Scholar  * Ping, L., Wu, Y., Hosu, B. G., Tang, J. X. &

Berg, H. C. Osmotic pressure in a bacterial swarm. _Biophys. J._ 107, 871–878 (2014). Article  ADS  MATH  Google Scholar  * Be’er, A. & Harshey, R. M. Collective motion of

surfactant-producing bacteria imparts superdiffusivity to their upper surface. _Biophys. J._ 101, 1017–1024 (2011). Article  ADS  Google Scholar  * Ke, W. J., Hsueh, Y. H., Cheng, Y. C., Wu,

C. C. & Liu, S. T. Water surface tension modulates the swarming mechanics of Bacillus subtilis. _Front. Microbiol._ 6, 1–12 (2015). Article  MATH  Google Scholar  * Ilkanaiv, B.,

Kearns, D. B., Ariel, G. & Beer, A. Effect of Cell Aspect Ratio on Swarming Bacteria. _Phys. Rev. Lett._ 118, 1–5 (2017). Article  MATH  Google Scholar  * Peled, S. et al. Heterogeneous

bacterial swarms with mixed lengths. _Phys. Rev. E_ 103, 1–7 (2021). Article  MathSciNet  MATH  Google Scholar  * Sidortsov, M., Morgenstern, Y. & Be’er, A. Role of tumbling in bacterial

swarming. _Phys. Rev. E_ 96, 1–7 (2017). Article  MATH  Google Scholar  * Mariconda, S., Wang, Q. & Harshey, R. M. A mechanical role for the chemotaxis system in swarming motility.

_Mol. Microbiol._ 60, 1590–1602 (2006). Article  MATH  Google Scholar  * Yashunsky, V., Pearce, D. J. G., Ariel, G. & Be’er, A. Topological defects in multi-layered swarming bacteria.

_Soft Matter_ 20, 4237–4245 (2024). Article  ADS  MATH  Google Scholar  * Hallatschek, O. et al. Proliferating active matter. https://doi.org/10.1038/s42254-023-00593-0. * Pérez-Estay, B.,

Cordero, M. L., Sepúlveda, N. & Soto, R. Accumulation and depletion of E. coli in surfaces mediated by curvature. _Phys. Rev. E_ 109, 1–9 (2024). Article  MATH  Google Scholar  *

Peruani, F., Deutsch, A. & Bär, M. Nonequilibrium clustering of self-propelled rods. _Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys_. 74, (2006). * Huang, M. J., Schofield, J.,

Gaspard, P. & Kapral, R. From single particle motion to collective dynamics in Janus motor systems. _J. Chem. Phys_. 150, (2019). * Garza, R. R., Kyriakopoulos, N., Cenev, Z. M., Rigoni,

C. & Timonen, J. V. I. Magnetic Quincke rollers with tunable single-particle dynamics and collective states. _Sci. Adv._ 9, 2–9 (2023). Google Scholar  * Zheng, X. et al. Non-Gaussian

statistics for the motion of self-propelled Janus particles: experiment versus theory. _Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys._ 88, 1–11 (2013). Article  ADS  MATH  Google Scholar

  * Zheng, E. et al. Self-oscillation and synchronization transitions in elastoactive structures. _Phys. Rev. Lett._ 130, 178202 (2023). Article  ADS  Google Scholar  * Bär, M., Großmann,

R., Heidenreich, S. & Peruani, F. Self-propelled rods: insights and perspectives for active matter. _Annu. Rev. Condens. Matter Phys._ 11, 441–466 (2020). Article  ADS  MATH  Google

Scholar  * Ramaswamy, S. The mechanics and statistics of active matter. _Annu. Rev. Condens. Matter Phys._ 1, 323–345 (2010). Article  ADS  MATH  Google Scholar  * Worlitzer, V. M. et al.

_Biophysics underlying swarm biofilm transition_ 8152, 1–9 (2022). Google Scholar  * Sorkin, B., Be’er, A., Diamant, H. & Ariel, G. Detecting and characterizing phase transitions in

active matter using entropy. _Soft Matter_ 19, 5118–5126 (2023). Article  ADS  MATH  Google Scholar  * Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. Concentration

dependence of the collective dynamics of swimming bacteria. _Phys. Rev. Lett._ 98, 1–4 (2007). Article  MATH  Google Scholar  * Mezanges, X. et al. Modeling the role of water in Bacillus

subtilis colonies. _Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys._ 85, 1–9 (2012). Article  Google Scholar  * Wang, Q., Suzuki, A., Mariconda, S., Porwollik, S. & Harshey, R. M.

Sensing wetness: a new role for the bacterial flagellum. _EMBO J_ 24, 2034–2042 (2005). Article  Google Scholar  * Be’er, A. & Lereah, Y. Time-resolved, three-dimensional quantitative

microscopy of a droplet spreading on solid substrates. _J. Microsc._ 208, 148–152 (2002). Article  MathSciNet  Google Scholar  * Zhang, R., Turner, L. & Berg, H. C. The upper surface of

an _Escherichia coli_ swarm is stationary. _Proc. Natl. Acad. Sci. USA_ 107, 288–290 (2010). Article  ADS  MATH  Google Scholar  * Copeland, M. F., Flickinger, S. T., Tuson, H. H. &

Weibel, D. B. Studying the dynamics of flagella in multicellular communities of Escherichia coli by using biarsenical dyes. _Appl. Environ. Microbiol._ 76, 1241–1250 (2010). Article  ADS 

Google Scholar  * Partridge, J. D., Nhu, N. T. Q., Dufour, Y. S. & Harshey, R. M. Tumble suppression is a conserved feature of swarming motility. _MBio_ 11, 1–5 (2020). Article  MATH 

Google Scholar  * Turner, L., Zhang, R., Darnton, N. C. & Berg, H. C. Visualization of flagella during bacterial swarming. _J. Bacteriol._ 192, 3259–3267 (2010). Article  MATH  Google

Scholar  * Li, Y., Zhai, H., Sanchez, S., Kearns, D. B. & Wu, Y. Noncontact cohesive swimming of bacteria in two-dimensional liquid films. _Phys. Rev. Lett._ 119, 1–6 (2017). Article 

Google Scholar  * Blair, K. M., Turner, L., Winkelman, J. T., Berg, H. C. & Kearns, D. B. A molecular clutch disables flagella in the Bacillus subtilis biofilm. _Science_ 320, 1636–1638

(2008). Download references ACKNOWLEDGEMENTS We thank Carmit Ziv for sharing the DIC microscope, Eric Clément and Yilin Wu for discussions. This project has received funding from the

European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 955910. Support for this work comes from National Institutes of Health grant

R35GM131783 to DBK. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * The Albert Katz International School for Desert Studies, The Jacob Blaustein Institutes for Desert Research, Ben-Gurion

University of the Negev, Sede Boqer Campus, Midreshet Ben-Gurion, Israel Ajesh Jose * Laboratoire PMMH-ESPCI Paris, PSL Research University, Sorbonne University, University Paris-Diderot, 7,

Quai Saint-Bernard, Paris, France Benjamín Pérez-Estay * The Shmunis School of Biomedicine and Cancer Research, Faculty of Life Sciences, Tel Aviv University, Tel Aviv, Israel Shira Omer

Bendori & Avigdor Eldar * Department of Biology, Indiana University, Bloomington, Indiana, USA Daniel B. Kearns * Department of Mathematics, Bar-Ilan University, Ramat Gan, Israel Gil

Ariel * Zuckerberg Institute for Water Research, The Jacob Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede Boqer Campus, Midreshet Ben-Gurion, Israel

Avraham Be’er * Department of Physics, Ben-Gurion University of the Negev, Beer-Sheva, Israel Avraham Be’er Authors * Ajesh Jose View author publications You can also search for this author

inPubMed Google Scholar * Benjamín Pérez-Estay View author publications You can also search for this author inPubMed Google Scholar * Shira Omer Bendori View author publications You can also

search for this author inPubMed Google Scholar * Avigdor Eldar View author publications You can also search for this author inPubMed Google Scholar * Daniel B. Kearns View author

publications You can also search for this author inPubMed Google Scholar * Gil Ariel View author publications You can also search for this author inPubMed Google Scholar * Avraham Be’er View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.J., A.E., D.B.K., G.A., and A.B. designed research, A.J., B.P.E., and A.B. performed the

experiments, S.O.B., A.E., and D.B.K. provided the strains and mutants, A.J., B.P.E., A.E., D.B.K., G.A., and A.B. analyzed data, A.J., B.P.E., S.O.B., A.E., D.B.K., G.A., and A.B. wrote the

paper. CORRESPONDING AUTHOR Correspondence to Avraham Be’er. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no conflict of interests. PEER REVIEW PEER REVIEW INFORMATION

_Communications Physics_ thanks the anonymous reviewers for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with

regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY MOVIE S1 SUPPLEMENTARY

MOVIE S2 SUPPLEMENTARY MOVIE S3 REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0

International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s)

and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material

derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a

credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted

use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions

ABOUT THIS ARTICLE CITE THIS ARTICLE Jose, A., Pérez-Estay, B., Bendori, S.O. _et al._ Immobility of isolated swarmer cells due to local liquid depletion. _Commun Phys_ 8, 88 (2025).

https://doi.org/10.1038/s42005-025-01996-4 Download citation * Received: 27 August 2024 * Accepted: 10 February 2025 * Published: 04 March 2025 * DOI:

https://doi.org/10.1038/s42005-025-01996-4 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative