Long-lived period-doubled edge modes of interacting and disorder-free floquet spin chains

ABSTRACT Floquet spin chains have been a venue for understanding topological states of matter that are qualitatively different from their static counterparts by, for example, hosting _π_

edge modes that show stable period-doubled dynamics. However the stability of these edge modes to interactions has traditionally required the system to be many-body localized in order to

suppress heating. In contrast, here we show that even in the absence of disorder, and in the presence of bulk heating, _π_ edge modes are long lived. Their lifetime is extracted from exact

diagonalization and is found to be non-perturbative in the interaction strength. A tunneling estimate for the lifetime is obtained by mapping the stroboscopic time-evolution to dynamics of a

single particle in Krylov subspace. In this subspace, the _π_ edge mode manifests as the quasi-stable edge mode of an inhomogeneous Su-Schrieffer-Heeger model whose dimerization vanishes in

the bulk of the Krylov chain. SIMILAR CONTENT BEING VIEWED BY OTHERS FLOQUET PRETHERMALIZATION IN DIPOLAR SPIN CHAINS Article 04 January 2021 QUANTUM PHASE TRANSITION AND COMPOSITE

EXCITATIONS OF ANTIFERROMAGNETIC SPIN TRIMER CHAINS IN A MAGNETIC FIELD Article Open access 27 November 2024 PRECURSORS OF MAJORANA MODES AND THEIR LENGTH-DEPENDENT ENERGY OSCILLATIONS

PROBED AT BOTH ENDS OF ATOMIC SHIBA CHAINS Article Open access 07 March 2022 INTRODUCTION Periodically driven or Floquet systems are promising venues for identifying states of matter that do

not exist in thermal equilibrium1. Perhaps the most striking among these athermal states are Floquet systems with new topological properties and bulk boundary correspondences that require

defining new topological invariants2,3. For example, while a static two-band system may be characterized by an integer \({\mathbb{Z}}\) valued or a \({{\mathbb{Z}}}_{2}\) valued topological

invariant4,5,6, two-band free fermion Floquet systems require at least one more topological invariant so that the system has a \({\mathbb{Z}}\times {\mathbb{Z}}\) or a

\({{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{2}\) classification7,8,9. The additional topological invariant arises due to the periodic nature of the Floquet spectrum. In particular, since the

energy in a periodically driven system is conserved only up to integer multiples of the drive frequency Ω, one has quasi-energy bands rather than energy bands. These quasi-energy bands span

a Floquet Brillouin zone (FBZ), \(\epsilon \in \left[-{{\Omega }}/2,{{\Omega }}/2\right]\), with the boundaries of the FBZ being continuous. The additional topological invariant

characterizes edge modes that can reside at the zone boundaries _ϵ_ = ±Ω/2. For two dimensional systems, the additional topological invariant leads to the anomalous Floquet insulator where a

bulk has zero Chern number, yet chiral edge modes propagate at the boundary10,11,12,13. For one dimensional (1d) systems, the edge modes that reside at the Floquet zone boundary are known

as _π_ edge modes14,15,16. Since these modes have a periodicity which is twice that of the drive period, they are examples of boundary time crystals17,18,19. Of course, the

\({\mathbb{Z}}\times {\mathbb{Z}}\) or a \({{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{2}\) classification implies that 0 and _π_ edge modes can exist separately, or together, leading to a rich

phase diagram20,21,22,23. The _π_ edge modes occurring in most 1d systems14,15,16,24 also have their origin in what are known as strong _π_ modes (SPM)25, whose precise definition we now

give. Denoting the _π_ strong mode as Ψ_π_, these are operators that have the property that they anti-commute with a discrete, say \({{\mathbb{Z}}}_{2}\) symmetry, which we denote by

\({{{{{{{\mathcal{D}}}}}}}}\). Thus, \(\{{{{\Psi }}}_{\pi },{{{{{{{\mathcal{D}}}}}}}}\}=0\). In addition, the SPM anti-commutes with the Floquet unitary _U_ that generates stroboscopic

time-evolution, {Ψ_π_, _U_} ≈ 0. The symbol ≈ is to represent the fact that the anti-commutation is strictly speaking obeyed only in the thermodynamic limit. For a finite size system of

length _L_, {Ψ_π_, _U_} ∝ ∣_u_∣_L_, where ∣_u_∣ < 1, so that the anti-commutator is suppressed exponentially in the system size. The third feature of the SPM is that it is a local

operator with the property \({{{\Psi }}}_{\pi }^{2}=O(1)\). The existence of a SPM implies an eigenspectrum phase where each eigenstate \(\left|n\right\rangle\) of a certain parity has a

pair \({{{\Psi }}}_{\pi }\left|n\right\rangle\) of the opposite parity, with the quasi-energies of the two states separated by _π_/_T_, where _T_ = 2_π_/Ω is the period of the drive. Note

that the above definition of SPMs can be generalized to more complex 2_π_/_k_ edge modes where _k_ is an integer26. When interactions are included, these operators no longer exactly

anti-commute with _U_ in the thermodynamic limit, and therefore acquire a lifetime. Yet a fascinating aspect of these edge modes, which is the central topic of this paper, is that the

lifetime far exceeds bulk heating times25. These quasi-stable edge modes that almost, rather than exactly anti-commute with _U_, are referred to as almost strong _π_ modes (ASPM). When

disorder is present, the expectation is that many-body localization will make the SPM stable to interactions at all times20,27,28,29,30,31. This paper, in contrast, concerns the stability of

_π_ modes for disorder-free chains, and determines how their lifetime depends on interactions. There are of course other contexts, besides ASPMs, where disorder-free Floquet systems can be

stable to interactions for long times32,33,34,35,36,37. An analogous definition exists for a strong zero mode (SZM) Ψ038,39,40,41. This is a local operator that obeys all the above

properties except that Ψ0 commutes with the Floquet unitary in the thermodynamic limit \(\left[{{{\Psi }}}_{0},U\right]\approx 0\). Thus existence of a SZM implies an eigenspectrum phase

where the entire spectrum of _U_ is at least doubly degenerate. Adding interactions makes the SZM into a quasi-stable almost strong zero mode (ASZM). Since SZMs and ASZMs have by now been

discussed in detail in static systems42,43,44,45,46,47, in this paper we will only focus on SPMs and ASPMs. A central goal of this paper is to establish how the lifetime of the _π_ mode

depends on interactions. In the process we present Krylov time-evolution as a tool for studying Floquet dynamics. This approach has so far only been employed for static

Hamiltonians46,47,48,49,50. Here we show how Krylov techniques can be used to extract tunneling times of quasi-stable modes of driven systems. We will study the stroboscopic dynamics of an

open spin-1/2 chain of length _L_. The dimension of the Hilbert space of the problem is 2_L_. The natural numerical method of choice is exact diagonalization (ED), and we are limited to a

system size of _L_ = 14. Since we are interested in extracting lifetimes in the thermodynamic limit of _L_ → _∞_, ED can be restrictive, and alternate numerical and analytical methods are

needed. Thus the results presented here, besides being an explication of the unusual physics of ASPMs, also provide a roadmap for developing methods for understanding slow, system size

independent dynamics. RESULTS AND DISCUSSION MODEL We will study an open chain of length _L_ whose stroboscopic time-evolution is generated by the following Floquet unitary

$$U={e}^{-i\frac{T}{2}{J}_{z}{H}_{zz}}{e}^{-i\frac{T}{2}{J}_{x}{H}_{xx}}{e}^{-i\frac{T}{2}g{H}_{z}},$$ (1) where $${H}_{z}=\mathop{\sum }\limits_{i=1}^{L}{\sigma

}_{i}^{z};\,{H}_{xx}=\mathop{\sum }\limits_{i=1}^{L-1}{\sigma }_{i}^{x}{\sigma }_{i+1}^{x};\,{H}_{zz}=\mathop{\sum }\limits_{i=1}^{L-1}{\sigma }_{i}^{z}{\sigma }_{i+1}^{z}.$$ (2) Above

_σ__x_,_y_,_z_ are the Pauli matrices, and in what follows we set _J__x_ = 1. Equation (1) is an example of a ternary drive where during one period, a magnetic field of strength _T__g_ is

applied, followed by the application of a nearest neighbor exchange interaction of strength _T_ along the _x_ direction, and this is followed by the application of a nearest neighbor

exchange interaction of strength _T__J__z_ along the _z_-direction. The Floquet unitary has a discrete symmetry as it commutes with \({{{{{{{\mathcal{D}}}}}}}}={\sigma }_{1}^{z}\ldots

{\sigma }_{L}^{z}\). When _J__z_ = 0, the model can be mapped to free fermions through a Jordan-Wigner transformation. In this free limit any operator can be expanded in a basis of 2_L_

Majorana fermions or Pauli string operators. Thus when _J__z_ = 0, the dimension of the space needed to diagonalize the problem is only 2_L_ rather than the dimension of the full Hilbert

space 2_L_. The existence of this free limit has been valuable for identifying strong modes. In fact, at the special point of _T__g_ = _π_, the Floquet unitary for _J__z_ = 0 reduces to

\(U={(-i)}^{L}{{{{{{{\mathcal{D}}}}}}}}{e}^{-i\frac{T}{2}{J}_{x}{H}_{xx}}\)20. At this special point, the SPM is simply the Pauli spin operator on the first site \({{{\Psi }}}_{\pi }={\sigma

}_{1}^{x}\). It is straightforward to check that \({\sigma }_{1}^{x}\) has all the properties of a SPM as summarized in the Introduction. It is a local operator with \({{{\Psi }}}_{\pi

}^{2}=1\), it anti-commutes with \({{{{{{{\mathcal{D}}}}}}}}\), and it anti-commutes with _U_. Even away from this special point, although the SPM is a more complex operator, it continues to

have the property that it has a non-zero overlap with \({\sigma }_{1}^{x}\)15,25. Including interactions, i.e, _J__z_ ≠ 0, as anticipated in the Introduction, the SPM changes to an ASPM.

Moreover, this operator continues to have an overlap with \({\sigma }_{1}^{x}\) for weak interactions. Therefore, an efficient way to determine whether the system hosts these special edge

modes is through the study of the following autocorrelation function $${A}_{\infty }(nT)=\frac{1}{{2}^{L}}{{{{{{{\rm{Tr}}}}}}}}\left[{\sigma }_{1}^{x}(nT){\sigma }_{1}^{x}(0)\right],$$ (3a)

$${\sigma }^{x}(nT)={\left[{U}^{{{{\dagger}}} }\right]}^{n}{\sigma }_{1}^{x}{U}^{n}.$$ (3b) We only study the dynamics at stroboscopic times, so _n_ is an integer. Moreover, _A__∞_ is an

infinite temperature average as the trace is over the entire Hilbert space. Thus this quantity is a highly out of equilibrium measure of the system dynamics. When an ASPM or an ASZM is

non-existent or if we replace \({\sigma }_{1}^{x}\) by an operator deep in the bulk of the chain, _A__∞_ will decay to zero within a few drive cycles. Throughout this paper, all numerical

results will be for _g_ = 0.3 and _T_ = 8.25, but for different values of _J__z_. For this value of _g_, _T_, when _J__z_ = 0 we have a SPM. When _J__z_ is non-zero, the SPM changes to an

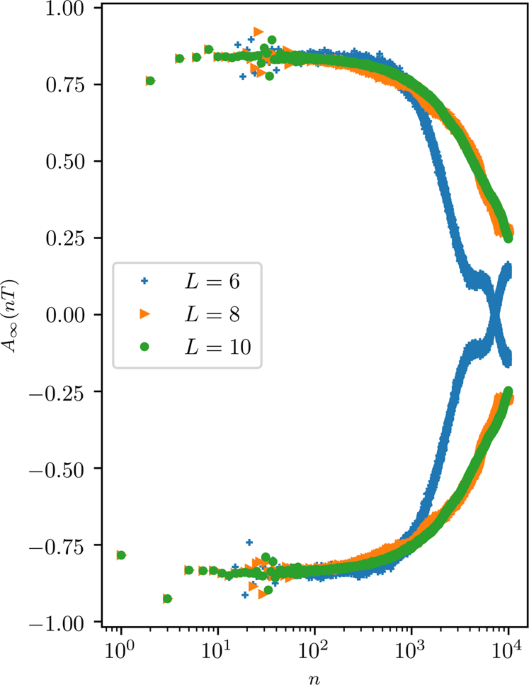
ASPM. EXACT DIAGONALIZATION (ED) We first present results for the stroboscopic time-evolution of _A__∞_ from ED. Figure 1 plots _A__∞_ for _J__z_ = 0.01, for three different system sizes _L_

 = 6, 8, 10. The _x_-axis which denotes the stroboscopic times is on a logarithmic scale. One finds that _A__∞_ flips sign between neighboring stroboscopic times, thus we have an ASPM.

Moreover, for small system sizes, as _L_ increases, the lifetime of the ASPM increases (compare _L_ = 6 with _L_ = 8 in the figure), but eventually the lifetime reaches a system size

independent value. For the chosen parameters, the system size independent lifetime is reached by _L_ = 8 as the plots for _L_ = 8 and _L_ = 10 nearly coincide. We refer to this system size

independent lifetime as the lifetime in the thermodynamic limit. Moreover, for _J__z_ = 0.01, this lifetime is around 104 drive cycles. Note that the high frequency limit requires _T_ ≪ 1,

and since we have _T_ = 8.25, we are far from the high frequency limit. Thus, the bulk is in fact heating, as expected for a periodically driven interacting, and disorder-free

system51,52,53,54,55. The evidence from ED for bulk heating was already presented in ref. 25, where it was shown that the autocorrelation function for bulk operators decays to zero within a

few drive cycles, and that the entropy density rapidly approaches the maximum possible value (accounting for finite size effects). Further below we discuss the signature of bulk heating in

Krylov subspace. We also extend the results of ref. 25 by extracting the interaction dependence of the lifetime of the _π_-mode using several different approaches: ED, Krylov dynamics, and

domain wall counting. We now discuss how the lifetime in the thermodynamic limit depends on _J__z_. Figure 2 shows the autocorrelation function accounting for its period-doubled behavior

\({A}_{\infty }^{p}(nT)={(-1)}^{n}{A}_{\infty }(nT)\). Since the sign-flipping of _A__∞_ is absorbed by the (−1)_n_ factor, \({A}_{\infty }^{p}\) has a smoother behavior in time. We plot

\({A}_{\infty }^{p}\) for different _J__z_ and for system sizes _L_ = 8, 10, 12, 14. The smallest possible _J__z_ we can study is _J__z_ = 0.001 because for _J__z_ values smaller than this,

the system size needed for the lifetime to become _L_ independent, is larger than _L_ = 14. While the stroboscopic times in Fig. 1 were linearly separated, the stroboscopic times in Fig. 2

are logarithmically separated as the lifetimes increase dramatically with decreasing _J__z_, and linearly separated points are numerically too costly to compute. Figure 2 clearly shows that

as _J__z_ increases (panels (a–g)), the lifetime of the ASPM decreases. In fact the thermodynamic lifetimes are already reached for _L_ = 8 when _J__z_ = 0.01 as the plots for all the four

system sizes lie on top of each other (panel (g)). Recall that Fig. 1 is a more detailed version of _A__∞_ for precisely this value of _J__z_, where the stroboscopic times are linearly

separated, and one smaller system size, _L_ = 6, is shown in order to highlight the system size dependence. We employ the ansatz that \({A}_{\infty }^{p}(nT)={e}^{-{{\Gamma }}nT}{A}_{\infty

}^{p}({n}_{0}T)\), where we choose _n_0 = 10 as it takes about 10 drive cycles for the initial transients to decay. The decay rate Γ is extracted from determining the time at which

\({A}_{\infty }^{p}({{{\Gamma }}}^{-1})\approx {e}^{-1}{A}_{\infty }^{p}(10T)\). This ansatz is plotted in Fig. 2 and captures the time-evolution very well. The decay rates Γ are plotted in

Fig. 3 where now it is the _y_-axis that is plotted on a logarithmic scale. The almost linear slope for 1/_J__z_ ≫ 1 suggests that (restoring _J__x_) $${{\Gamma }} \sim

{e}^{-c{J}_{x}/{J}_{z}}.$$ (4) Above _c_ is a _O_(1) number that depends on _g_, _J__x_. Thus for small enough _J__z_, ED indicates that the decay rates are non-perturbative in the strength

of the interactions _J__z_. As _J__z_ is further increased, we do not expect the edge mode to be an ASPM, and its decay rate will be determined entirely by perturbative processes \({{\Gamma

}}\propto O({J}_{z}^{\alpha })\), where _α_ is a power of _O_(1). KRYLOV SUBSPACE DYNAMICS In order to understand the origin of the non-perturbatively long lifetimes for _J__z_ ≪ 1, and its

relation to bulk heating, we map the stroboscopic time-evolution of \({\sigma }_{1}^{x}\) to dynamics of a free particle in a Krylov subspace employing a recursive Lanczos

scheme48,49,50,56,57. This mapping to single particle physics will allow us to develop a tunneling picture for the lifetime of the ASPM. Let us define the Floquet Hamiltonian as

\({H}_{F}=i\ln (U)/T\). The stroboscopic time-evolution after _m_ periods of a Hermitian operator _O_ can be written in terms of _H__F_ as follows $${\left[{U}^{{{{\dagger}}}

}\right]}^{m}O{U}^{m}={e}^{i{H}_{F}mT}O{e}^{-i{H}_{F}mT}=\mathop{\sum }\limits_{n=0}^{\infty }\frac{{(imT)}^{n}}{n!}{{{{{{{{\mathcal{L}}}}}}}}}^{n}O,$$ (5) where we define

\({{{{{{{\mathcal{L}}}}}}}}O=[{H}_{F},O]\). To employ the Lanczos algorithm, we recast the operator dynamics into vector dynamics by defining \(\left|O\right)=O\). Since we are concerned

with infinite temperature quantities, we have an unambiguous choice for an inner product on the level of the operators, \((A| B)=\,{{\mbox{Tr}}}\,\left[{A}^{{{{\dagger}}}

}B\right]/{2}^{L}\). The Lanczos algorithm iteratively finds the operator basis that tri-diagonalizes \({{{{{{{\mathcal{L}}}}}}}}\). We begin with the seed “state”, \(\left|{O}_{1}\right)\),

and let \({{{{{{{\mathcal{L}}}}}}}}\left|{O}_{1}\right)={b}_{1}\left|{O}_{2}\right)\), where \({b}_{1}=\sqrt{| {{{{{{{\mathcal{L}}}}}}}}\left|{O}_{1}\right){| }^{2}}\). The recursive

definition for the basis operators \(\left|{O}_{n\ge 2}\right)\) is, \({{{{{{{\mathcal{L}}}}}}}}\left|{O}_{n}\right)={b}_{n}\left|{O}_{n+1}\right)+{b}_{n-1}\left|{O}_{n-1}\right)\), where we

define \({b}_{n\ge 2}=\sqrt{| {{{{{{{\mathcal{L}}}}}}}}\left|{O}_{n}\right)-{b}_{n-1}\left|{O}_{n-1}\right){| }^{2}}\). It is straightforward algebra to check that the above procedure will

yield a \({{{{{{{\mathcal{L}}}}}}}}\) of the form $${{{{{{{\mathcal{L}}}}}}}}=\left(\begin{array}{llll}&{b}_{1}&&\\ {b}_{1}&&{b}_{2}&\\ &{b}_{2}&&\ddots

\\ &&\ddots &\end{array}\right).$$ (6) The basis spanned by \(\left|{O}_{n}\right)\) lies within the Krylov subspace of \({{{{{{{\mathcal{L}}}}}}}}\) and

\(\left|{O}_{1}\right)\). We refer to this tri-diagonal matrix as the Krylov Hamiltonian _H__K_, \({H}_{K}={\sum }_{n}{b}_{n}({c}_{n}^{{{{\dagger}}} }{c}_{n+1}+{c}_{n+1}^{{{{\dagger}}}

}{c}_{n})\), and the 1d lattice it represents, as the Krylov chain. For free systems, the operation \({{{{{{{\mathcal{L}}}}}}}}\left|{O}_{n}\right)\) can be efficiently solved in the

Majorana basis. If the starting operator is a single Majorana, then the dimension of the Krylov subspace of that operator will scale as 2_L_, as free system dynamics can only mix the

individual Majoranas among themselves. Outside of free problems, the size of the full set of ∣_O__n_) will be large. For example, a system of size _L_ will have ~ 22_L_ possible basis

operators. Since we are interested in the thermodynamic limit for the lifetime of the edge operator, in what follows, we will treat the Krylov chain to be a semi-infinite chain. The Krylov

chain of interest to us is the one where the seed operator \(\left|{O}_{1}\right)=\left|{\sigma }_{1}^{x}\right)\). Then _A__∞_ is equivalent to \({A}_{\infty

}(nT)={({e}^{i{{{{{{{\mathcal{L}}}}}}}}nT})}_{1,1}\). Thus the dynamics of _A__∞_ has been transformed into that of a semi-infinite, single-particle problem where _A__∞_(_n__T_) is now the

probability that a particle initially localized at the end of the Krylov chain, stays localized at the end at time _n__T_. As a point of orientation, let us discuss the details of the Krylov

subspace in the free limit. In the Majorana basis, the stroboscopic time evolution of an operator \(\overrightarrow{a}={\left[{a}_{1},{a}_{2},\ldots {a}_{2L}\right]}^{T}\) is (see

Supplementary Note 1) $${U}^{{{{\dagger}}} }\overrightarrow{a}U=K\overrightarrow{a},$$ (7) where _K_ is a 2_L_ × 2_L_ orthogonal matrix and the _a__i_ are Majoranas with \({a}_{1}={\sigma

}_{1}^{x}\). For studying SM dynamics, our seed operator is \(\overrightarrow{a}={\left[{a}_{1},0,0,0\ldots \right]}^{T}\). The components of _K_ can be determined analytically. On comparing

Eqs. (5) and (7), we identify the operator \(iT{{{{{{{\mathcal{L}}}}}}}}\) with \(\ln K\). Since \({{{{{{{\mathcal{L}}}}}}}}\) is an operator, whose precise form depends on the basis, we

have argued that the Krylov Hamiltonian _H__K_ is related to \(i\ln K\) by a simple basis rotation. The form of \(i\ln K\) becomes particularly simple close to the exactly solvable point

_g__T_ = _π_ and in the high frequency limit _T_ ≪ 1. Denoting \({s}_{1}=\sin (gT)\), in the first order in _s_1 and _T_ we find (see Supplementary Note 1) $$i\ln K\approx

\left(\begin{array}{llllll}0&i{s}_{1}&0&0&0&0\\ -i{s}_{1}&0&-iT&0&0&0\\ 0&iT&0&i{s}_{1}&0&0\\

0&0&-i{s}_{1}&0&-iT&0\\ 0&0&0&iT&0&i{s}_{1}\\ 0&0&0&0&-i{s}_{1}&0\end{array}\right)\pm \pi .$$ (8) The analytic result in Eq. (8)

shows that \(i\ln K\) is like a Su-Schrieffer-Heeger (SSH) model58,59 with a topologically non-trivial dimerization for ∣_s_1∣ < _T_. Moreover the overall shift of _π_ ensures that the

edge mode of the SSH model is pinned at _π_ rather than at zero energy. The SSH model is a band insulator with a band-gap controlled by the strength of the dimerization ∣∣_s_1∣ − _T_∣. In

contrast, when the dimerization is zero, the model is a trivial metal. We will see below that switching on interactions leads to inhomogeneities such that insulating regions of non-zero

dimerization coexist with metallic regions of zero dimerization. In the limit where Eq. (8) is valid, we can derive the Krylov Hamiltonian analytically (see Supplementary Note 1). We find

that _b_odd = ∣_s_1∣, _b_even = _T_, with a constant term ± _π_ along the diagonals. Thus when ∣_s_1∣ < _T_, the Krylov Hamiltonian is a topologically non-trivial SSH model that hosts a

zero mode. The constant term along the diagonal shifts its energy to _π_. The _b__n_s for _g_ = 0.3 and _T_ = 8.25, and for the free case _J__z_ = 0 are shown in Fig. 4a. For this case,

∣_s_1∣ and _T_ are no longer small. Thus there are differences in the Krylov parameters between this case, and the exact solution around _g__T_ ≈ _π_ just discussed. One is that the Krylov

Hamiltonian has zeros on the diagonals away from the exactly solvable limit. The second is that the hopping on the very first site is large. However, as suggested by the analytic form in the

exactly solvable limit, the Krylov chain is a SSH model with a uniform dimerization after _n_ ≿ 4. Figure 4b shows the corresponding spectrum of the Krylov chain, where the three horizontal

red lines are at _ϵ_ = 0, ±_π_. Modes at ±_π_ that are also separated from the bulk modes by a gap, are clearly visible. Thus we see that even though the diagonal term of the Krylov chain

is zero, it is the initial large hopping of _b_1 ≈ _π_ that ensures that the edge modes of the SSH model are pinned at ±_π_. In fact the effective model for the Krylov chain for _J__z_ = 0

can be written as _H__K_ = _H_SSH + _H__E_, where _H_SSH represents a SSH model and captures the behavior from sites _n_ ≿ 4, while _H__E_ is an edge Hamiltonian that captures the physics on

the first few sites. The SPM _ψ__π_ is a zero mode of _H_SSH, while _H__E__ψ__π_ = _π__ψ__π_. Thus _H__K__ψ__π_ = _π__ψ__π_. To obtain a _π_ edge mode, the parameters of _H__E_ are finely

tuned, while _H_SSH only requires its dimerization to be topologically non-trivial to ensure a zero mode. The role of _H__E_ is to raise the energy of the zero mode to _π_. Note that this

mapping from the Floquet unitary _U_ to the Krylov chain has lost information about the periodic nature of the spectrum of _U_, and this manifests as finely tuned _b__n_ at the edge of the

Krylov chain when a _π_ mode exists. Nevertheless this mapping to an effectively free model helps to arrive at a tunneling estimate for the lifetime of the _π_ mode when interactions are

non-zero. We discuss this below. We now switch on interactions. We expect the dynamics to explore larger regions of the Hilbert space, resulting in more complicated _b__n_. These are shown

in Fig. 5b–e for system size _L_ = 12 and with different _J__z_. Figure 5g–j show the corresponding spectra. For easy comparison between the free and interacting cases, Fig. 5a, f correspond

to _J__z_ = 0. The blue circles (all panels Fig. 5) correspond to carrying out the Lanczos procedure in the spin basis, which is the natural choice when interactions are present. In

contrast, the free case involved performing Lanczos in the Majorana basis Fig. 5a, f. The periodicity of _U_ is lost in the Lanczos approach, and the resulting _b__n_ are sensitive to the

choice of the branch of \(\ln (U)\). This leads to _b__n_s (blue circles Fig. 5b–e), which do not bear much of a resemblance to the _b__n_s of the free case Fig. 5a, making them harder to

interpret. In particular, the free _b__n_s have a perfectly dimerized form for _n_ > 3, and therefore a periodicity of 2. In contrast, the _b__n_s shown by the blue circles (Fig. 5b–e)

have a longer periodicity, close to 3. The spectra for the spin basis are shown in Fig. 5g–j (blue circles). These spectra are not restricted to the FBZ. In addition, the periodicity of 3

manifests as 3 gaps for the spectra shown by the blue circles (Fig. 5g–j), with the gaps located at ±_π_, 0. These gaps are most clearly visible for the smallest _J__z_ = 0.001 (Fig. 5g). In

contrast, the spectra of the free _b__n_s (Fig. 5f) have only two gaps. The additional gap in the spectra shown by the blue circles arises because the system has lost information that the

quasi-energy spectra are continuous with _π_ being the same as −_π_. One may map the dynamics to an alternate Krylov subspace using an Arnoldi iteration scheme60 that works directly with the

Floquet unitary, rather than its logarithm, and therefore bypasses some of the ambiguities of the Lanczos iteration. Alternatively, below we devise a scheme that can extract the relevant

physics from Lanczos by a suitable gauge choice. Since the spectra are periodic, a physically more suitable gauge choice for the Krylov Hamiltonian is the one where the spectra are folded

back to lie within the FBZ (orange crosses in Fig. 5g–j). This folding requires transforming the Krylov Hamiltonian \({H}_{K}\to {U}_{K}{\hat{\epsilon

}}_{{{{{{{{\rm{FBZ}}}}}}}}}{U}_{K}^{{{{\dagger}}} }\), where \({\hat{\epsilon }}_{{{{{{{{\rm{FBZ}}}}}}}}}\) is a diagonal matrix where all the energies lie in the FBZ, and _U__K_ is the

unitary matrix that diagonalizes _H__K_ before the folding. The folding procedure is non-local, and therefore gives a new Hamiltonian, which is no longer tri-diagonal. Therefore, a second

Lanczos iteration is carried out to recover the tri-diagonal form, resulting in a new set of _b__n_s that are shown by orange crosses in Fig. 5b–e. After this transformation, the new _b__n_s

bear a closer resemblance to the _b__n_s of the free case, thus making them easier to interpret. In comparison to the free case, one notices that a dimerization persists even with

interactions, but is non-uniform, and gradually decreases into the bulk of the chain. This is visible in both gauges, i.e., blue circles and orange stars in Fig. 5a–e. The larger _J__z_ is,

the more rapidly the dimerization decays into the chain. The contrast is most visible between _J__z_ = 0.001 (Fig. 5b) and _J__z_ = 0.05 (Fig. 5e). The region of the chain where there is no

dimerization, represents a metallic state. Thus we have a spatially inhomogeneous system in the presence of _J__z_ where a disordered insulating region (represented by spatially fluctuating

but non-zero dimerization) is separated from a metallic bulk. An operator with weight in the metallic bulk will spread rapidly, and its autocorrelation function will decay to zero within a

few drive cycles. The existence of the metal is the signature of bulk heating because the metal has no localized states. The emergence of the metal is especially clear after the folding

procedure where the gaps at zero quasi-energy begin to fill up after the folding, compare folded spectra represented by orange stars with the unfolded spectra represented by blue circles in

Fig. 5g–j. Recall that for the free case the dimerization exists throughout the bulk. Thus the structure of the _b__n_s for _J__z_ ≠ 0 gives us evidence that a quasi-localized edge mode can

exist despite bulk heating. The above picture also clarifies how the ASPM acquires a lifetime. Essentially the edge mode is localized initially at the left end of the chain, and is separated

by a finite region of dimerization from the metallic bulk. Therefore, it has a non-zero probability of tunneling into the metallic region. Below we estimate the lifetime of the ASPM by

determining this tunneling probability. In order to make the discussion more quantitative, in Fig. 6a we plot the dimerization, i.e., absolute value of the nearest-neighbor _b__n_s, _M_(_n_)

 = _b__n_+1 − _b__n_, corresponding to the data represented by the orange stars of Fig. 5. We plot this quantity after performing a moving average over 4 sites, and denote it as

〈∣_M_(_n_)∣〉4. (See Supplementary Note 2 and Supplementary Fig. 1 for the data without the averaging, and with only 2-site averaging for comparison.) We note that 〈∣_M_(_n_)∣〉4 does not

change with _J__z_ for the first couple of sites (provided _J__z_ < 0.05), while away from the edge, 〈∣_M_(_n_)∣〉4 decreases with _n_ when _J__z_ ≠ 0. In contrast, 〈∣_M_(_n_)∣〉4 stays

constant for the free case. The fact that the first few sites of the Krylov chain do not change with _J__z_ implies that _H__E_ is not sensitive to _J__z_. We therefore adopt a simple model

of a Krylov chain for the sites _n_ ≿ 4, with two slowly varying parameters, a nearest-neighbor average hopping (_b__n_ + _b__n_−1)/2, and the dimerization _M_(_n_)46,47 (see Supplementary

Note 3). We now emphasize some important differences between the _b__n_s for the ASZM in static systems46,47 and the same for the ASPM for Floquet systems. One is the sensitivity to gauge

choice for the latter due to the freedom in shifting the quasi-energies by integer multiples of 2_π_ (see detailed discussion above). The second difference is that when the Floquet spectrum

is bounded by the FBZ, the average _b__n_s do not increase unboundedly with _n_, unlike in static systems. Thus we derive a continuum model under the assumption that the nearest-neighbor

average hopping is spatially uniform, and that the dimerization is slowly varying in space. These assumptions map the Krylov chain onto a Dirac model with a spatially inhomogeneous mass (see

Supplementary Note 3) \(i{\partial }_{t}\tilde{{{\Psi }}}=\left[m(X){\sigma }^{y}+{\sigma }^{x}i{\partial }_{X}\right]\tilde{{{\Psi }}}\), where _m_(_n_) = _M_(2_n_). For _J__z_ = 0, the

mass is spatially uniform and topologically non-trivial, _m_ > 0, with _M_(2_n_) = − _M_(2_n_ + 1) = _m_. For _J__z_ ≠ 0, this mass vanishes into the bulk. While the precise model for how

it vanishes is complicated, we adopt a simple ansatz where _m_(_X_) = _M_0_θ_(_X_ − _X_0). Then a WKB treatment shows that the lifetime of the edge mode is (see Supplementary Note 3)

\({{\Gamma }}\approx 4{M}_{0}{e}^{-2{M}_{0}{X}_{0}}\). The fact that the edge mode is at _π_ energy rather than at zero energy enters in the boundary condition via _H__E_, where a strong

local hopping pins the edge mode to _π_. We now discuss the _J__z_ dependence of _M_0. Figure 6b shows that \({\langle | M(n = 24)| \rangle }_{4} \sim {J}_{z}^{-1}\). Since the decay-rate Γ

depends on the mass _M_0 exponentially, and _M_0 ∝ 1/_J__z_, we conclude that \({{\Gamma }} \sim {e}^{-c/{J}_{z}}\). BOUND FOR LIFETIME FROM DOMAIN WALL COUNTING ARGUMENT We now present an

alternate argument for the non-perturbatively long lifetime in Eq. (4). We show below that despite the low frequency driving, the energy required to flip the spin on the very first site is

highly off-resonant, and requires rearranging many domain walls in the bulk. This phenomena was also noted in previous studies on static systems42,45,46,61. Thus the boundary is in a

prethermal state62,63,64,65,66, despite the thermalized bulk. We argue this physics by deriving a Floquet Hamiltonian _H__F_ in the limit of _J__z_ ≪ 1 and ∣_g__T_ − _π_∣ ≪ 1. Recall _g__T_ 

= _π_ and _J__z_ = 0 is the exactly solvable limit where the SPM is \({{{\Psi }}}_{\pi }={\sigma }_{1}^{x}\). Let us define \({\hat{J}}_{z}={J}_{z}T/2,\hat{g}=Tg/2-\pi /2\) and

\({\hat{J}}_{x}=T{J}_{x}/2\). We will work in the limit \({\hat{J}}_{x}\gg 1\) and \({\hat{J}}_{z},\hat{g}\ll 1\). We cannot perform a high-frequency expansion67 to construct _H__F_ as

\({\hat{J}}_{x}\) is not small. Nevertheless, _H__F_ to first order in \({\hat{J}}_{z},\hat{g}\) but to arbitrary orders in \({\hat{J}}_{x}\) may be derived from an infinite resummation of

the Baker-Campbell-Hausdorff formula68,69, leading to the following non-local perturbed Ising model25 $$T{H}_{F}\approx \;{\hat{J}}_{x}{H}_{xx}+\frac{\pi

}{2}{{{{{{{\mathcal{D}}}}}}}}+\hat{g}\left\{{h}_{z}^{E}{\hat{J}}_{x}\cot ({\hat{J}}_{x})+{h}_{z}^{B}\left(\frac{1+2{\hat{J}}_{x}\cot (2{\hat{J}}_{x})}{2}\right)\right.\\

+\left.{h}_{xzx}\left(\frac{-1+2{\hat{J}}_{x}\cot (2{\hat{J}}_{x})}{2}\right)-{\hat{J}}_{x}\left({h}_{xy}+{h}_{yx}\right)\right\}\\ +{\hat{J}}_{z}\left\{{h}_{zz}^{E}{\hat{J}}_{x}\cot

({\hat{J}}_{x})+{h}_{zz}^{B}\left(\frac{1+2{\hat{J}}_{x}\cot (2{\hat{J}}_{x})}{2}\right)\right.\\ -\left.{h}_{xyyx}\left(\frac{-1\!+\!2{\hat{J}}_{x}\cot

(2{\hat{J}}_{x})}{2}\right)\!+\!{\hat{J}}_{x}\left({h}_{zyx}\!+\!{h}_{xyz}\right)\right\}\!+\!O({\hat{g}}^{2},{\hat{J}}_{z}^{2}).$$ (9) Above \({h}_{{\alpha }_{1}\ldots {\alpha }_{k}}={\sum

}_{j}{\sigma }_{j}^{{\alpha }_{1}}\ldots {\sigma }_{j+k-1}^{{\alpha }_{k}}\equiv {h}_{{\alpha }_{1}\ldots {\alpha }_{k}}^{E}+{h}_{{\alpha }_{1}\ldots {\alpha }_{k}}^{B}\), where _h__E_

denotes the contributions from the edge spins \({\sigma }_{1,L}^{\alpha }\) and _h__B_ denotes the bulk spins. Let us consider the energetics involved in flipping \({\sigma }_{1}^{x}\) for

\(\hat{g}={\hat{J}}_{z}=0\). Since the boundary spin has only one neighbor, this flip costs energy \({\hat{J}}_{x}\). However, the energy cost for creating a domain wall in the bulk is

\(2{\hat{J}}_{x}\) due to the two neighboring sites. Thus there is a mismatch of \({\hat{J}}_{x}\gg 1\) between a bulk and an edge excitation, making the flipping of an edge spin impossible.

However this simple argument does not account for processes that can make the domain wall hop from site to site, resulting in a lowering of its energy. Thus, we have to revisit the energy

argument by accounting for the kinetic energy of the domain walls. In order to develop our argument, we first note that _H__x__x_ counts the number of domain-walls \(N={\sum }_{i}{\sigma

}_{i}^{x}{\sigma }_{i+1}^{x}\). Therefore, we write _H__F_ as a part that commutes with the number of domain walls, and a part that changes the number of domain walls. In particular,

\(T{H}_{F}={\hat{J}}_{x}N+D+V\) where \(\left[D,N\right]=0\) and \(\left[V,N\right]\ne 0\). Both _D_ and _V_ can be written in the form similar to Eq. (9), i.e., as sums over local strings

of Pauli matrices. The precise forms of _D_ and _V_ are not needed for our qualitative argument. We only assume that the operator norms of each of the local terms of _D_ and _V_ are

\(O(\hat{g},{\hat{J}}_{z})\). If these assumptions are valid we can apply the arguments of refs. 42,45,46,61 to find a lower bound on the lifetime of the ASPM. Here, we briefly summarize the

physical picture. First, consider the Hamiltonian \({\hat{J}}_{x}N+D\). The spectrum of the \({\hat{J}}_{x}\)-term are states that are separated by multiples of \({\hat{J}}_{x}\) because

_N_ counts domain walls. The _D_-term causes the domain walls to move without changing their number. Diagonalization of \({\hat{J}}_{x}N+D\) results in domain wall “bands” with a typical

bandwidth \(\epsilon \sim | | D| | \sim O(\hat{g},{\hat{J}}_{z})\) which is much smaller than the separation \({\hat{J}}_{x}\) between the bands. The _V_-term of the total Hamiltonian does

change the number of domain walls, but only by an even number due to the parity symmetry of the total Hamiltonian. A single application of _V_ therefore changes the energy by about

\(2{\hat{J}}_{x}\) and is off resonant with the cost \({\hat{J}}_{x}\) of flipping the boundary spin. It is impossible to absorb the energy \({\hat{J}}_{x}\) within few orders of

perturbation theory in _V_. However, the creation and annihilation of a pair of domain walls would lead to the change of the energy by the order of the bandwidth \(\epsilon \ll

{\hat{J}}_{x}\). Therefore, we estimate that one needs of the order of \({\hat{J}}_{x}/\epsilon\) powers of _V_ to offset the energy \({\hat{J}}_{x}\) required to flip a boundary spin. The

probability corresponding to the required order of perturbation theory goes as \({\left[| | V| | \right]}^{{\hat{J}}_{x}/\epsilon } \sim {\left[| | V| | \right]}^{{J}_{x}/O({J}_{z},g)}\)

where ∣∣_V_∣∣ denotes the typical size of the matrix element that creates a domain wall. The above expression is a lower bound for the lifetime. For example, in the two integrable limits

(which is a property of the exact rather than the approximate _H__F_) _J__z_ → 0, _g_ ≠ 0 and _g_ → 0, _J__z_ ≠ 0, the lifetime should diverge. Empirically combining this observation with

the rough estimate above we expect 1/_ϵ_ = _O_(1/_J__z_, 1/_g_). When _J__z_ ≪ _g_ this empirical formula replaces _ϵ_ → _J__z_ in the above estimate making it consistent with Eq. (4).

CONCLUSIONS ASPMs are fascinating objects which have lifetimes that far exceed bulk heating times. Besides presenting evidence for this, we developed a method for extracting their lifetimes

by mapping their dynamics to single-particle quantum mechanics in Krylov subspace. While we studied the lifetime for _J__z_ ≪ _g_, determining the lifetime when _g_, _J__z_ are comparable is

left for future studies. Our Krylov method for determining lifetimes is generalizable to any spatial dimension, to closed and open systems, and to static and driven systems. In addition,

the resistance to heating of the _π_ mode is promising for its experimental realization70. DATA AVAILABILITY All relevant data are available from the corresponding author upon reasonable

request. REFERENCES * Oka, T. & Kitamura, S. Floquet engineering of quantum materials. _Annu. Rev. Cond. Matter Phys._ 10, 387 (2019). Article  ADS  Google Scholar  * Rudner, M. S. &

Lindner, N. H. Band structure engineering and non-equilibrium dynamics in floquet topological insulators. _Nat. Rev. Phys_ 2, 229 (2020). Article  Google Scholar  * Harper, F., Roy, R.,

Rudner, M. S. & Sondhi, S. Topology and broken symmetry in floquet systems. _Annu. Rev. Cond. Matter Phys._ 11, 345 (2020). Article  Google Scholar  * Ryu, S., Schnyder, A. P., Furusaki,

A. & Ludwig, A. W. W. Topological insulators and superconductors: tenfold way and dimensional hierarchy. _N. J. Phys._ 12, 065010 (2010). Article  Google Scholar  * Qi, X.-L. &

Zhang, S.-C. Topological insulators and superconductors. _Rev. Mod. Phys._ 83, 1057 (2011). Article  ADS  Google Scholar  * Bernevig, B. A. _Topological Insulator and Topological

Superconductors_ (Princeton University Press, Princeton, 2013). * Carpentier, D., Delplace, P., Fruchart, M. & Gawedzki, K. Topological index for periodically driven time-reversal

invariant 2d systems. _Phys. Rev. Lett._ 114, 106806 (2015). Article  ADS  MathSciNet  MATH  Google Scholar  * Roy, R. & Harper, F. Abelian floquet symmetry-protected topological phases

in one dimension. _Phys. Rev. B_ 94, 125105 (2016). Article  ADS  Google Scholar  * Roy, R. & Harper, F. Periodic table for floquet topological insulators. _Phys. Rev. B_ 96, 155118

(2017). Article  ADS  Google Scholar  * Kitagawa, T., Berg, E., Rudner, M. & Demler, E. Topological characterization of periodically driven quantum systems. _Phys. Rev. B_ 82, 235114

(2010). Article  ADS  Google Scholar  * Rudner, M. S., Lindner, N. H., Berg, E. & Levin, M. Anomalous edge states and the bulk-edge correspondence for periodically driven two-dimensional

systems. _Phys. Rev. X_ 3, 031005 (2013). Google Scholar  * Nathan, F., Rudner, M. S., Lindner, N. H., Berg, E. & Refael, G. Quantized magnetization density in periodically driven

systems. _Phys. Rev. Lett._ 119, 186801 (2017). Article  ADS  Google Scholar  * Titum, P., Berg, E., Rudner, M. S., Refael, G. & Lindner, N. H. Anomalous floquet-anderson insulator as a

nonadiabatic quantized charge pump. _Phys. Rev. X_ 6, 021013 (2016). Google Scholar  * Jiang, L. et al. Majorana fermions in equilibrium and in driven cold-atom quantum wires. _Phys. Rev.

Lett._ 106, 220402 (2011). Article  ADS  Google Scholar  * Thakurathi, M., Patel, A. A., Sen, D. & Dutta, A. Floquet generation of majorana end modes and topological invariants. _Phys.

Rev. B_ 88, 155133 (2013). Article  ADS  Google Scholar  * Asbóth, J. K., Tarasinski, B. & Delplace, P. Chiral symmetry and bulk-boundary correspondence in periodically driven

one-dimensional systems. _Phys. Rev. B_ 90, 125143 (2014). Article  ADS  Google Scholar  * Sacha, K. & Zakrzewski, J. Time crystals: a review. _Rep. Prog. Phys._ 81, 016401 (2017).

Article  ADS  MathSciNet  Google Scholar  * Else, D. V., Monroe, C., Nayak, C. & Yao, N. Y. Discrete time crystals. _Annu. Rev. Cond. Matter Phys._ 11, 467 (2020). Article  Google

Scholar  * Khemani, V., Moessner, R. & Sondhi, S. A brief history of time crystals. Preprint at https://arxiv.org/abs/1910.10745 (2019). * Khemani, V., Lazarides, A., Moessner, R. &

Sondhi, S. L. Phase structure of driven quantum systems. _Phys. Rev. Lett._ 116, 250401 (2016). Article  ADS  Google Scholar  * von Keyserlingk, C. W., Khemani, V. & Sondhi, S. L.

Absolute stability and spatiotemporal long-range order in floquet systems. _Phys. Rev. B_ 94, 085112 (2016). Article  ADS  Google Scholar  * von Keyserlingk, C. W. & Sondhi, S. L. Phase

structure of one-dimensional interacting floquet systems. i. abelian symmetry-protected topological phases. _Phys. Rev. B_ 93, 245145 (2016). Article  ADS  Google Scholar  * von Keyserlingk,

C. W. & Sondhi, S. L. Phase structure of one-dimensional interacting floquet systems. ii. symmetry-broken phases. _Phys. Rev. B_ 93, 245146 (2016). Article  ADS  Google Scholar  *

Bastidas, V. M., Emary, C., Schaller, G. & Brandes, T. Nonequilibrium quantum phase transitions in the ising model. _Phys. Rev. A_ 86, 063627 (2012). Article  ADS  Google Scholar  *

Yates, D. J., Essler, F. H. L. & Mitra, A. Almost strong (0, _π_) edge modes in clean interacting one-dimensional floquet systems. _Phys. Rev. B_ 99, 205419 (2019). Article  ADS  Google

Scholar  * Sreejith, G. J., Lazarides, A. & Moessner, R. Parafermion chain with 2_π_/_k_ floquet edge modes. _Phys. Rev. B_ 94, 045127 (2016). Article  ADS  Google Scholar  * Huse, D.

A., Nandkishore, R. & Oganesyan, V. Phenomenology of fully many-body-localized systems. _Phys. Rev. B_ 90, 174202 (2014). Article  ADS  Google Scholar  * Bahri, Y., Ronen, R. &

Altman, E. Localization and topology protected quantum coherence at the edge of hot matter. _Nat. Commun._ 6, 7341 (2015). Article  ADS  Google Scholar  * Else, D. V., Bauer, B. & Nayak,

C. Floquet time crystals. _Phys. Rev. Lett._ 117, 090402 (2016). Article  ADS  Google Scholar  * Potirniche, I.-D., Potter, A. C., Schleier-Smith, M., Vishwanath, A. & Yao, N. Y.

Floquet symmetry-protected topological phases in cold-atom systems. _Phys. Rev. Lett._ 119, 123601 (2017). Article  ADS  Google Scholar  * Kumar, A., Dumitrescu, P. T. & Potter, A. C.

String order parameters for one-dimensional floquet symmetry protected topological phases. _Phys. Rev. B_ 97, 224302 (2018). Article  ADS  Google Scholar  * Zeng, T.-S. & Sheng, D. N.

Prethermal time crystals in a one-dimensional periodically driven floquet system. _Phys. Rev. B_ 96, 094202 (2017). Article  ADS  Google Scholar  * Haldar, A., Moessner, R. & Das, A.

Onset of floquet thermalization. _Phys. Rev. B_ 97, 245122 (2018). Article  ADS  Google Scholar  * Haldar, A., Sen, D., Moessner, R. & Das, A. Dynamical freezing and scar points in

strongly driven floquet matter: Resonance vs emergent conservation laws. _Phys. Rev. X_ 11, 021008 (2021). Google Scholar  * Chandran, A. & Sondhi, S. L. Interaction-stabilized steady

states in the driven _o_(_n_) model. _Phys. Rev. B_ 93, 174305 (2016). Article  ADS  Google Scholar  * Natsheh, M., Gambassi, A. & Mitra, A. Critical properties of the floquet time

crystal within the gaussian approximation. _Phys. Rev. B_ 103, 014305 (2021). Article  ADS  Google Scholar  * Natsheh, M., Gambassi, A. & Mitra, A. Critical properties of the prethermal

floquet time crystal. _Phys. Rev. B_ 103, 224311 (2021). Article  ADS  Google Scholar  * Kitaev, A. Y. Unpaired majorana fermions in quantum wires. _Physics-Uspekhi_ 44, 131 (2001). Article

  ADS  Google Scholar  * Fendley, P. Parafermionic edge zero modes in _z__n_ -invariant spin chains. _J. Stat. Mech. Theory Exp._ 2012, P11020 (2012). Article  MathSciNet  MATH  Google

Scholar  * Jermyn, A. S., Mong, R. S. K., Alicea, J. & Fendley, P. Stability of zero modes in parafermion chains. _Phys. Rev. B_ 90, 165106 (2014). Article  ADS  Google Scholar  *

Fendley, P. Strong zero modes and eigenstate phase transitions in the xyz/interacting majorana chain. _J. Phys. A Math. Theor._ 49, 30LT01 (2016). Article  MathSciNet  MATH  Google Scholar 

* Else, D. V., Fendley, P., Kemp, J. & Nayak, C. Prethermal strong zero modes and topological qubits. _Phys. Rev. X_ 7, 041062 (2017). Google Scholar  * Kemp, J., Yao, N. Y., Laumann, C.

R. & Fendley, P. Long coherence times for edge spins. _J. Stat. Mech. Theory Exp._ 2017, 063105 (2017). Article  MathSciNet  MATH  Google Scholar  * Parker, D. E., Vasseur, R. &

Scaffidi, T. Topologically protected long edge coherence times in symmetry-broken phases. _Phys. Rev. Lett._ 122, 240605 (2019). Article  ADS  Google Scholar  * Kemp, J., Yao, N. Y. &

Laumann, C. R. Symmetry-enhanced boundary qubits at infinite temperature. _Phys. Rev. Lett._ 125, 200506 (2020). Article  ADS  Google Scholar  * Yates, D. J., Abanov, A. G. & Mitra, A.

Lifetime of almost strong edge-mode operators in one-dimensional, interacting, symmetry protected topological phases. _Phys. Rev. Lett._ 124, 206803 (2020). Article  ADS  Google Scholar  *

Yates, D. J., Abanov, A. G. & Mitra, A. Dynamics of almost strong edge modes in spin chains away from integrability. _Phys. Rev. B_ 102, 195419 (2020). Article  ADS  Google Scholar  *

Vishwanath, V & Müller, G. The recursion method: applications to many-body dynamics (Springer, New York, 2008). * Dymarsky, A. & Gorsky, A. Quantum chaos as delocalization in krylov

space. _Phys. Rev. B_ 102, 085137 (2020). Article  ADS  Google Scholar  * Avdoshkin, A. & Dymarsky, A. Euclidean operator growth and quantum chaos. _Phys. Rev. Res._ 2, 043234 (2020).

Article  Google Scholar  * Kim, H., Ikeda, T. N. & Huse, D. A. Testing whether all eigenstates obey the eigenstate thermalization hypothesis. _Phys. Rev. E_ 90, 052105 (2014). Article 

ADS  Google Scholar  * Lazarides, A., Das, A. & Moessner, R. Equilibrium states of generic quantum systems subject to periodic driving. _Phys. Rev. E_ 90, 012110 (2014). Article  ADS 

Google Scholar  * D’Alessio, L. & Rigol, M. Long-time behavior of isolated periodically driven interacting lattice systems. _Phys. Rev. X_ 4, 041048 (2014). Google Scholar  * Ponte, P.,

Chandran, A., Papić, Z. & Abanin, D. A. Periodically driven ergodic and many-body localized quantum systems. _Ann. Phys._ 353, 196 (2015). Article  ADS  MathSciNet  MATH  Google Scholar

  * Bukov, M., Heyl, M., Huse, D. A. & Polkovnikov, A. Heating and many-body resonances in a periodically driven two-band system. _Phys. Rev. B_ 93, 155132 (2016). Article  ADS  Google

Scholar  * Parker, D. E., Cao, X., Avdoshkin, A., Scaffidi, T. & Altman, E. A universal operator growth hypothesis. _Phys. Rev. X_ 9, 041017 (2019). Google Scholar  * Barbón, J.,

Rabinovici, E., Shir, R. & Sinha, R. On the evolution of operator complexity beyond scrambling. _J. High Energy Phys._ 2019, 264 (2019). Article  ADS  MathSciNet  MATH  Google Scholar  *

Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. _Phys. Rev. Lett._ 42, 1698 (1979). Article  ADS  Google Scholar  * Su, W. P., Schrieffer, J. R. & Heeger, A.

J. Soliton excitations in polyacetylene. _Phys. Rev. B_ 22, 2099 (1980). Article  ADS  Google Scholar  * Arnoldi, W. E. The principle of minimized iterations in the solution of the matrix

eigenvalue problem. _Quart. Appl. Math._ 9, 17 (1951). Article  MathSciNet  MATH  Google Scholar  * Else, D. V., Bauer, B. & Nayak, C. Prethermal phases of matter protected by

time-translation symmetry. _Phys. Rev. X_ 7, 011026 (2017). Google Scholar  * Abanin, D. A., De Roeck, W. & Huveneers, F. Exponentially slow heating in periodically driven many-body

systems. _Phys. Rev. Lett._ 115, 256803 (2015). Article  ADS  Google Scholar  * Kuwahara, T., Mori, T. & Saito, K. Floquet-magnus theory and generic transient dynamics in periodically

driven many-body quantum systems. _Ann. Phys._ 367, 96 (2016). Article  ADS  MathSciNet  MATH  Google Scholar  * Mori, T., Kuwahara, T. & Saito, K. Rigorous bound on energy absorption

and generic relaxation in periodically driven quantum systems. _Phys. Rev. Lett._ 116, 120401 (2016). Article  ADS  Google Scholar  * Abanin, D. A., De Roeck, W., Ho, W. W. & Huveneers,

F. Effective hamiltonians, prethermalization, and slow energy absorption in periodically driven many-body systems. _Phys. Rev. B_ 95, 014112 (2017). Article  ADS  Google Scholar  * Abanin,

D., De Roeck, W., Ho, W. W. & Huveneers, F. A rigorous theory of many-body prethermalization for periodically driven and closed quantum systems. _Commun. Math. Phys._ 354, 809 (2017).

Article  ADS  MathSciNet  MATH  Google Scholar  * Eckardt, A. & Anisimovas, E. High-frequency approximation for periodically driven quantum systems from a floquet-space perspective. _N.

J. Phys._ 17, 093039 (2015). Article  MATH  Google Scholar  * Scharf, R. The campbell-baker-hausdorff expansion for classical and quantum kicked dynamics. _J. Phys. A Math. Gen._ 21, 2007

(1988). Article  ADS  MathSciNet  MATH  Google Scholar  * D’Alessio, L. & Polkovnikov, A. Many-body energy localization transition in periodically driven systems. _Ann. Phys._ 333, 19

(2013). Article  ADS  MathSciNet  MATH  Google Scholar  * Liu, D. T., Shabani, J. & Mitra, A. Floquet majorana zero and _π_ modes in planar josephson junctions. _Phys. Rev. B_ 99, 094303

(2019). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, under Award No.

DE-SC0010821 (D.J.Y. and A.M.) and by the US National Science Foundation Grant NSF DMR-1606591 (A.G.A.). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Center for Quantum Phenomena,

Department of Physics, New York University, 726 Broadway, New York, NY, 10003, USA Daniel J. Yates & Aditi Mitra * Simons Center for Geometry and Physics, Stony Brook, NY, 11794, USA

Alexander G. Abanov * Department of Physics and Astronomy, Stony Brook University, Stony Brook, NY, 11794, USA Alexander G. Abanov Authors * Daniel J. Yates View author publications You can

also search for this author inPubMed Google Scholar * Alexander G. Abanov View author publications You can also search for this author inPubMed Google Scholar * Aditi Mitra View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.J.Y. and A.M. performed the numerical and analytical calculations. A.G.A. and A.M. helped in the

interpretation of the results and in the writing of the manuscript. CORRESPONDING AUTHOR Correspondence to Aditi Mitra. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no

competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Physics_ thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports

are available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY

INFORMATION SUPPLEMENTARY MATERIAL PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits

use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the

Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yates, D.J., Abanov, A.G. & Mitra, A. Long-lived period-doubled edge modes of interacting and disorder-free Floquet spin chains. _Commun

Phys_ 5, 43 (2022). https://doi.org/10.1038/s42005-022-00818-1 Download citation * Received: 26 May 2021 * Accepted: 04 February 2022 * Published: 22 February 2022 * DOI:

https://doi.org/10.1038/s42005-022-00818-1 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative