Modulating the thermal conductivity in hexagonal boron nitride via controlled boron isotope concentration

ABSTRACT Hexagonal boron nitride (h-BN) has been predicted to exhibit an in-plane thermal conductivity as high as ~ 550 W m−1 K−1 at room temperature, making it a promising thermal

management material. However, current experimental results (220–420 W m−1 K−1) have been well below the prediction. Here, we report on the modulation of h-BN thermal conductivity by

controlling the B isotope concentration. For monoisotopic 10B h-BN, an in-plane thermal conductivity as high as 585 W m−1 K−1 is measured at room temperature, ~ 80% higher than that of h-BN

with a disordered isotope concentration (52%:48% mixture of 10B and 11B). The temperature-dependent thermal conductivities of monoisotopic h-BN agree well with first principles calculations

including only intrinsic phonon-phonon scattering. Our results illustrate the potential to achieve high thermal conductivity in h-BN and control its thermal conductivity, opening avenues for

the wide application of h-BN as a next-generation thin-film material for thermal management, metamaterials and metadevices. SIMILAR CONTENT BEING VIEWED BY OTHERS ALLOYING HBN WITH ALUMINUM

INFLUENCES ABSORPTION AND ELECTRONIC PROPERTIES Article Open access 22 March 2025 REVEALING POLYTYPISM IN 2D BORON NITRIDE WITH UV PHOTOLUMINESCENCE Article Open access 05 November 2024

ANOMALOUS ISOTOPE EFFECT ON MECHANICAL PROPERTIES OF SINGLE ATOMIC LAYER BORON NITRIDE Article Open access 01 September 2023 INTRODUCTION Hexagonal boron nitride (h-BN) is a technologically

important layered material used as a dielectric spacer, encapsulant, ultraviolet laser emitter, and hyperbolic material in electronic and photonic applications1,2,3. More recently, h-BN has

attracted attention for thermal management of electronics as theoretical calculations4 predicted an in-plane thermal conductivity as high as _k_r~ 550 W m−1 K−1 at room temperature, though,

highly anisotropic with a two orders of magnitude smaller out-of-plane thermal conductivity (_k_z~ 5 W m−1 K−1). The high in-plane thermal conductivity, as well as atomic flatness, makes

h-BN an ideal substrate material for next-generation thin-film devices since waste heat can be spread quickly laterally through a large area, avoiding formation of localized hot spots5,6. In

addition, h-BN could be a good reinforcing filler for thermal interface and encapsulation composite materials due to its high thermal conductivity and electrical resistivity7,8. Despite its

predicted favorable thermal properties, experimental results are few and varied. Reported _k_r values range from 220 to 420 W m−1 K−1 4,9,10, well below the predicted maximum value.

Developing insight into this discrepancy and driving h-BN thermal conductivity to higher values is of great interest both fundamentally and for enabling enhanced thermal engineering.

Quantized lattice vibrations (phonons) in crystals synthesized from elements with natural isotopic concentration scatter due to mass variations of the isotopes in the lattice, thus reducing

thermal conductivity11. Enhanced thermal conductivity has been demonstrated in monoisotopic materials (isotopically purified to >99% one isotope), such as in silicon12, germanium13,

gallium arsenide14, diamond15, and graphene16. Naturally occurring BN materials are made with two stable B isotopes (19.9% 10B and 80.1% 11B), which present a large mass modulation, and an

opportunity to control its thermal conductivity by manipulating the B isotope concentration. Large B isotope effect has been observed in BN nanotubes17, whereas experimental evidence of

isotope effects in h-BN has not been possible to date because suitable samples have not been available. In terms of theoretical predictions, the conventional Callaway approach13,18,19 based

on the Boltzmann transport equation (BTE) and formulated within a single-mode relaxation time approximation (RTA)  has been widely used to study the isotope effect in numerous material

systems, but has challenges in anisotropic layered systems such as h-BN. Often, phonon scattering processes in layered systems cannot be treated as independent resistive processes, an

assumption of the RTA20. Ab initio approaches based on full solution of the BTE in combination with first principles density functional theory (DFT) have demonstrated accuracy in describing

the thermal conductivity of anisotropic layered materials with natural isotopic concentrations21,22, however, experimental data for monoisotopic layered materials are not available for model

validations. Only recently have isotopically engineered h-BN crystals become available23,24,25. To date, investigations have focused on fundamental isotope effects related to Raman phonon

lifetimes and the electronic bandgap23,24. In this work, we experimentally demonstrate the effect of boron isotope concentration on the thermal conductivity of bulk h-BN crystals using a

transient thermoreflectance (TTR) technique. The monoisotopic 10B h-BN crystals have in-plane thermal conductivity as high as 585 W m−1 K−1 at room temperature, ~ 80% larger than that of

h-BN with disordered isotope concentrations (52%:48% mixture of 10B and 11B). Our measurements are compared with state-of-the-art ab initio thermal conductivity calculations. RESULTS H-BN

CRYSTALS AND MICROSTRUCTURAL CHARACTERIZATION h-BN crystals were prepared from monoisotopic boron powders (10B and 11B), with the process described in Liu et al.25. This allowed the control

of the boron isotope composition from 50%:50% (the most disordered composition) to monoisotopic 10B or 11B. Four h-BN crystals were grown, with input isotope compositions of 99% 10B

(monoisotopic 10B), 48% 11B (isotopically disordered), 78% 11B (near-natural), and 99% 11B (monoisotopic 11B), respectively (see Methods). Supplementary Fig. 1 shows an optical micrograph of

typical flake-like samples with size around 1 mm. Flake thicknesses were determined by optical microscopy to be 15 ± 2 µm by measuring the height difference between the sample surface and

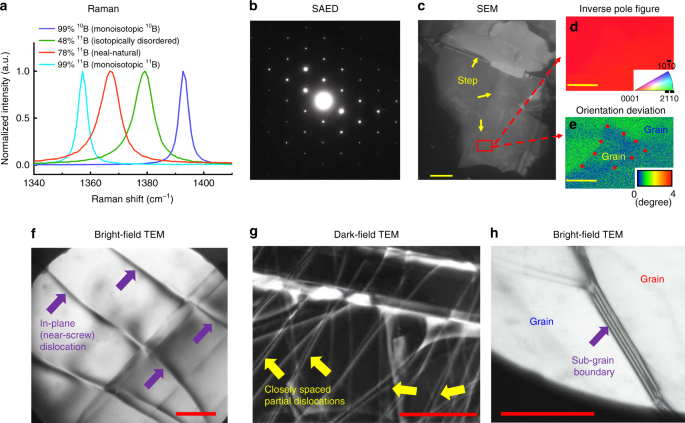
the underlying substrate. Figure 1a shows Raman spectra of the high-energy E2g mode from the different isotopically engineered h-BN crystals (see Methods). The energy of this E2g phonon is

1393 cm−1, 1379 cm−1, 1367 cm−1, and 1357 cm−1 for monoisotopic 10B, isotopically disordered, near-natural and monoisotopic 11B h-BN, respectively. The Raman shifts of the samples were

benchmarked against the established relationship between Raman shifts and the isotope ratios24, verifying that the resulting h-BN crystals have the same isotope ratios as the input material

(see details in Supplementary Note 1). As expected, the Raman linewidths are much narrower for the monoisotopic 10B h-BN (2.9 cm−1) and monoisotopic 11B h-BN (3.1 cm−1) than for the

isotopically disordered h-BN (7.6 cm−1) and near-natural h-BN (7.9 cm−1). The linewidths are in part determined by phonon–isotope interactions in the disordered materials, a feature that was

correlated with low-loss phonon-polariton modes in monoisotopic h-BN previously24. The crystal microstructure of the h-BN samples was characterized with selected area electron diffraction

(SAED), transmission electron microscopy (TEM), scanning electron microscopy (SEM), and electron back-scattered diffraction (EBSD) (see Methods), with results shown in Fig. 1b–h from a

representative h-BN specimen (monoisotopic 10B h-BN; for results of all samples see Supplementary Fig. 2). The SAED pattern (Fig. 1b) showed a single-oriented hexagonal crystal structure

consistent with a [0001] surface. The SEM image (Fig. 1c) and EBSD inverse pole figure (Fig. 1d) confirmed the size of single crystal domains are larger than >150 μm. There were steps

between these large domains, which are natural features in hexagonal crystals grown from solutions26. Using TEM, the single crystal domain was found to have areas a few tens of microns

across which are free of defects. In some locations, in-plane (near-screw) dislocations with Burgers vectors \({\mathrm{a}}/3\langle 11\bar 20\rangle\) were observed, as seen in the

bright-field TEM image in Fig. 1f. Such dislocations describe a rotation about [0001] between successive layers, estimated to be up to ~0.02° in Fig. 1f. In the dark-field TEM in Fig. 1g,

taken in weak-beam diffracting conditions, the in-plane perfect dislocations are seen to be dissociated into closely spaced partial \({\mathrm{a}}/3\langle 10\bar 10\rangle\) dislocations on

a fine scale. In some areas, sub-grain boundaries were observed, visible as fringes in the bright-field TEM image in Fig. 1h. The boundary indicates the misorientation (tilt) between the

two grains with the misorientation angle estimated to be up to ~ 1°. This conclusion is consistent with that from EBSD (Fig. 1e). The misorientations (tilt) between the grains across the

sample were small, about 2° or less. In short, the fabricated h-BN samples had high-quality large single-crystalline domains with a very low density of dislocations and tilt. ANISOTROPIC

THERMAL CONDUCTIVITY CHARACTERIZATION The thermal conductivity of h-BN, _k_r—in-plane and _k_z—out-of-plane, were measured using a nano-second laser-based TTR technique27,28,29 (see

Methods). Figure 2a shows the schematics of the TTR technique. The h-BN crystal was coated with a 50 nm Au thin film, which serves as a transducer. A 10 ns, 355 nm pulsed pump laser heats

the surface of the Au transducer, creating a temperature response. A continuous 532 nm laser was used to monitor the surface temperature response via the induced change in Au reflectivity.

Figure 2b shows an example of the monitored normalized thermoreflectance transient. An analytical photothermal pulses-induced thermal transport model was built based on the geometric and

temporal characteristics of the pump pulse, experimental structure and boundary conditions shown in Fig. 2c to analyze the measured transients. We use \(S_{x_0} = \frac{{\partial \left(

{{\mathrm{ln}}T} \right)}}{{\partial \left( {{\mathrm{ln}}x_0} \right)}}\) to quantify the sensitivity of the temperature response (_T_) to the parameter, _x_0, which is either of the

thermal conductivities of h-BN (_k_r, _k_z) or the thermal boundary resistance between the Au transducer and h-BN (_TBR_eff) (see Methods). Figure 2d shows the calculated sensitivity

results. The sensitivity to _k_z (_S_z) and _TBR_eff (_S_TBR) increases rapidly from 10 to 100 ns, whereas sensitivity to _k_r (_S_r) remains mostly constant. With further increasing time,

_S_z remains relatively constant and _S_TBR increases slowly, whereas _S_r gradually increases and exceeds _S_TBR and _S_z at ~ 500 ns. Taking advantage of the distinct sensitivity time

scales of the thermoreflectance transients, the parameters, _k_z, _k_r, and _TBR_eff, were determined simultaneously via fitting the monitored TTR transients with the analytical thermal

transport model (see Methods). The best fit of our model results to an example measured transient for the monoisotopic 10B h-BN sample at 300 K is given in Fig. 2b. The ±25% bound curves

shown in Fig. 2b illustrate that TTR signals are mainly sensitive to _k_z at short time scales (10–500 ns) and more sensitive to _k_r at longer time scales (>500 ns). Figures 3a, b give

the measured values of _k_r and _k_z for the four crystals, as a function of temperature. Also shown are the results of (BTE)/(DFT) calculations using three-phonon and phonon–isotope

scattering from quantum perturbation methods as inputs4 (see Methods). The predicted curves for monoisotopic 10B h-BN and 11B h-BN give the h-BN intrinsic thermal conductivities determined

solely by three-phonon scattering processes. Theory and experiment for _k_r are in good quantitative agreement for the monoisotopic h-BN for temperatures >150 K. Discrepancies for <150

 K are likely due to the extrinsic scattering of phonons from crystal imperfections not included in the theoretical calculations. Such extrinsic defects may include sub-grain boundaries,

dislocations (apparent in TEM micrographs Fig. 1f–h), and point defects such as vacancies and carbon impurities (carbon impurity concentrations of 7.5–27 × 1019 cm−3 have been measured in

h-BN crystals grown from identical synthesis methods24). The phonon mean free paths in h-BN at 100–150 K range from a few hundred nanometers to 10 μm, and the lower the temperature the

longer the phonon mean free paths4. This suggests that sub-grain boundaries are a possible contributor to reducing the thermal conductivity of h-BN at low temperature considering the long

phonon mean free path is comparable to the grain size, as evident in TEM and EBSD micrographs (Figs 1e, h). Point defects, such as carbon impurities, may also scatter phonons as strongly as

isotope variations due to the mass and force fluctuations around the defect sites30,31. Such defects, like isotope variations, become more important at lower temperature where the intrinsic

phonon–phonon scattering is weak. Figure 3a also shows the theoretical _k_r of natural and isotopically disordered h-BN. The measured results compare well with theoretical calculations

>225 K; differences at lower temperatures again may arise from the presence of defects. As shown in Fig. 3b, the out-of-plane thermal conductivities (_k_z) for all samples compare

favorably with the calculations, over the temperature range measured. Weak van der Waals bonding between h-BN planes gives smaller acoustic velocities perpendicular to the planes, whereas

strong in-plane covalent bonding of the light B and N atoms gives fast phonons along the planes4. Thus, _k_z is much smaller than _k_r. There is a relatively small but apparent increase in

thermal conductivity for the monoisotopic samples compared with the disordered ones. Extrinsic phonon scattering from grain boundaries and point defects is expected to have a smaller effect

on _k_z due to the much shorter phonon mean free paths (about a few tens of nanometers4) in the out-of-plane direction, and therefore agreement between simulations and measurements over a

broader temperature range is found. The in-plane thermal conductivities _k_r of 585 ± 80 W m−1 K−1 and 550 ± 75 W m−1 K−1 measured at 300 K for the monoisotopic 10B and 11B h-BN,

respectively, are the highest room temperature values reported to date in the literature for h-BN. The measured _k_r value for near-natural h-BN (78% 11B) is 408 ± 60 W m−1 K−1 is consistent

with previously reported values for natural h-BN (80% 11B) by Sichel et al.10 and Jiang et al.4, and about twice larger than that measured by Simpson et al.9. Isotopically disordered h-BN

has the lowest measured _k_r, 330 ± 42 W m−1 K−1. At 300 K, the measured out-of-plane thermal conductivities, _k_z, are 3.5 ± 0.8 W m−1 K−1, 4.5 ± 1.4 W m−1 K−1, 3.3 ± 0.8 W m−1 K−1 and 2.3 

± 0.5 W m−1 K−1 for the monoisotopic 10B, monoisotopic 11B, near-natural and isotopically disordered h-BN crystals, respectively. All these values are comparable to those reported for

natural h-BN in Jiang et al.4 and Simpson et al.9. Note that the isotope effect on _k_z is not clearly distinguishable experimentally due to relatively large error bars of experimental data.

The calculations of _k_r and _k_z for monoisotopic 10B h-BN predict it to be somewhat larger than those of monoisotopic 11B h-BN, despite both systems being free of phonon–isotope

scattering. Phonon frequencies roughly scale with mass−1/2. This results in slightly faster acoustic phonons and less scattering from higher frequency optic phonons in monoisotopic 10B h-BN

compared with monoisotopic 11B h-BN. These both lead to larger thermal conductivities (_k_r and _k_z) in monoisotopic 10B h-BN. This variance is within the error bars of the measured data

and therefore not clearly distinguishable experimentally. The enhancement of the thermal conductivity, _k_r, in monoisotopic 10B h-BN and 11B h-BN, with respect to the natural BN is 43 and

35%, respectively, at room temperature. This is smaller than monoisotopic enhancements reported in graphene (~ 58%16) and diamond (~ 50%15), although the natural isotopic disorder and

resulting mass variance is larger in naturally occurring h-BN (19.9% 10B and 80.1% 11B) than in naturally occurring carbon materials (98.9% 12C and 1.1% 13C). One important factor to

consider when comparing the carbon-based materials and bulk h-BN is the discrepancy between the frequency scales of their phonon dispersions. Covalent C-C bonds are stronger than that of B-N

bonds, which results in “harder” phonons in graphene and diamond. Besides reducing acoustic phonon velocities, the softer phonons in h-BN exhibit two important effects, which reduce the

_k_r enhancement: (1) h-BN has weaker phonon–isotope scattering as this scales as frequency to the power four32, and (2) h-BN has stronger intrinsic phonon–phonon scattering as the phase

space for interactions increases as the dispersion frequency scale decreases33. The stronger intrinsic phonon scattering in h-BN compared with diamond and graphene is indirectly observed

when comparing the isotopically purified thermal conductivities: 585 ± 80 W m−1 K−1, ~ 4000 W m−1 K−1 16, and ~ 3300 W m−1 K−1 15 for monoisotopic 10B h-BN, graphene and diamond,

respectively. The predicted anisotropic ratio (_k_r/_k_z) is as high as 125 at 300 K, displayed in Fig. 3c, in reasonable agreement with measurements. We note that the difference in measured

_k_r/_k_z between monoisotopic and isotopically disordered samples is large (>40 for T < 200 K) despite the presence of point defects reducing _k_r at low temperatures. This

demonstrates that isotope engineering makes tuning of the thermal conductivity anisotropy possible in h-BN over a large range. Recently, tuning thermal anisotropy in materials has been

demonstrated to allow precise manipulation of heat flux including for heat shielding, heat concentrators, macroscopic diodes, chip heat management, and energy harvesting34,35,36,37,38.

Traditional thermal metamaterials used for these applications are designed from two or more constituent materials with large thermal conductivity contrast, to realize the required

anisotropic and inhomogenous conductivity profiles by spatially adjusting their volume filling ratios. Coefficient of thermal expansion contrast can then result in challenges including

mechanical instability and complicated fabrication processes35. Clearly, engineering materials via isotope concentration alone is more straightforward, and the resulting product is a single

phase material with negligible differences of heat capacity (see Supplementary Fig. 7), density23, and temperature-dependent lattice constant23 (leading to similar thermal expansion),

providing a promising route to enhanced thermal metamaterials and metadevices. DISCUSSION Through isotope engineering, we have experimentally demonstrated the manipulation of the thermal

conductivity of h-BN. The measured temperature-dependent thermal conductivity of monoisotopic h-BN provides a means for the verification of DFT calculations of thermal conductivity as solely

impacted by intrinsic phonon–phonon scattering processes. At room temperature, the in-plane thermal conductivity (_k_r) of monoisotopic 10B h-BN  was measured as high as 585 W m−1 K−1, the

highest room temperature values for h-BN reported in the literature, and in good agreement with theoretical predictions. The enhanced _k_r in monoisotopic h-BN makes it a promising candidate

for managing heat in higher power dissipation compact thin-film devices. A highly tuneable conductivity anisotropy ratio of h-BN by isotope engineering, may extend the application of h-BN

to thermal metamaterial and metadevice applications. METHODS H-BN CRYSTAL GROWTH h-BN single crystals were synthesized using the Ni-Cr flux method. High-purity 10B (99.22 at%) and 11B (99.41

at%) powders were mixed with Ni and Cr powders to give overall concentrations of 4 wt% B, 48 wt% Ni, and 48 wt% Cr. Manipulating the mass ratio of 10B to 11B in the source material renders

different isotope compositions of resulting h-BN crystals. After loading the crucible, the furnace was evacuated, then filled with N2 and forming gas (5% hydrogen in balance argon) to ~850 

torr. The N2 and forming gases continuously flowed through the system during crystal growth with flow rates of 125 sccm and 25 sccm, respectively. The system was heated to 1550 °C for a

dwell time of 24 h. The h-BN crystals were formed by cooling at a rate of 0.5 °C h−1 to 1525 °C, then quenched to room temperature. Four different mass ratios of 10B to 11B (100%:0, 50%:50%,

20%:80%, and 0:100%) were input as source material, resulting in four different isotope compositions (1, 48, 78, and 99% 11B) in the resulting h-BN crystals. Crystals ranged up to a few mm

in size. RAMAN MEASUREMENTS Raman measurements were performed using a 532 nm laser line with a Renishaw Raman microscope. In all, <10 mW laser power was directed at the sample through a

50 × 0.75 N.A. objective, with the Raman scattered light collected back through the same objective. The scattered light was dispersed using a 2400 groove mm−1 grating onto a silicon

charge-coupled device. The spectral positions of the Raman lines were calibrated against a silicon reference sample. For each h-BN crystal studied, four measurements were performed,

reporting the average spectral position and linewidth. MICROSCOPIC ANALYSIS SAED and TEM plan-view images were acquired at 200 kV in a Philips EM430 TEM. The dark-field and bright-field TEM

was operated in the two beam diffracting conditions with \(g = 11\bar 20\). SEM and EBSD measurements were performed on Zeiss Evo MA10 LaB6 with an instrument probe equipped with EBSD. The

EBSD mapping image was constructed by scanning a ~ 600 µm2 rectangular area with a 1 µm step size. Lattice constants of h-BN were taken from literature reported data23 for the EBSD analysis.

For the SAED and TEM analysis, small pieces of h-BN were crushed from the as-grown crystals and then adhered onto a holey silicon nitride support membrane for imaging. For the SEM and EBSD

analysis, the as-grown crystals were mounted on the carbon tape and the first few layers were exfoliated using Scotch tape to expose the clean surface for imaging. TTR MEASUREMENTS The TTR

measurement configuration is shown in Fig. 2a. To prepare the samples for the TTR measurements, the h-BN flakes were first cleaned with acetone, and then attached to a large glass slide

using carbon tape. The first few layers were exfoliated using Scotch tape, to create a clean surface, before depositing a 50 nm (±5%) Au transducer film, with a 10 nm Ti interlayer for good

adhesion. The Au film serves as a transducer in the TTR measurements. The schematic of TTR sample is shown in Fig. 2b mounted on a copper disk in the Linkam THMS600 cryostat, which was used

to control the sample temperature from 100 K to 300 K during the measurements. The pump beam is a 10 ns, 355 nm frequency tripled Nd:YAG laser with a 30 kHz repetition rate. After passing

through a beam expander and dichroic beam splitter, it is directed through a 15 × 0.3 N.A. quartz objective to a de-focused spot on the sample with a Gaussian profile (1/e2 radius of 41 μm).

The pump laser power incident at the sample surface is less than 5 mW (time averaged, peak of 15 W). The transient surface reflectivity change is monitored using a CW 532 nm laser probe

beam focused at the sample surface to 2 μm, in the central location of the pump spot. The reflected beam intensity is sampled by a beam splitter and detected by a silicon photodiode

transimpedence amplifier (2.3 ns rise time) and a digital oscilloscope (300 MHz bandwidth). To ensure no residual light from the pump beam is detected, a long-pass filter is placed before

the detector. We note alternative to TTR often time domain thermoreflectance (TDTR)39,40 is employed to measure thermal conductivity. However, TTR is more sensitive to anisotropy of thermal

conductivities. TDTR, typically uses ultrashort (fs/ps) high-frequency pulse lasers. As the thermal penetration depth of a short laser pulse is much smaller than that of the laser spot size,

one-dimensional heat transfer is generally assumed making the conventional TDTR insensitive to radial heat conduction. Although, e.g., pump and probe offset TDTR41 and variable pump spot

size TDTR42 has been employed to enable an increased sensitivity to radial heat conduction and hence allow measurement of anisotropic thermal conductivities, the TTR technique is easier to

use. ANALYTICAL PHOTOTHERMAL PULSES-INDUCED THERMAL TRANSPORT MODEL FOR THE ANALYSIS OF THE TTR DATA The thermal conductivity of h-BN was determined by comparing the measured TTR transients

with an analytical photothermal pulses-induced thermal transport model. The model considers heat conduction in _N_-layer films (in this study: _N_ = 3 (Au, Ti and h-BN layers)). The _i_-th

layer of the film with thickness _d__i_, is taken having an in-plane thermal conductivities (_k__i_-_r_), out-of-plane thermal conductivities (_k__i_-_z_), density (_ρ__i_), and specific

heat capacity _C__i_, with _i_ = 1, 2, …_N_. The material (carbon tape) used for mounting the h-BN sample, indexed as _N_ + 1, is considered a thermal insulator due to its low thermal

conductivity. At time _t_ = 0 when the system is in thermal equilibrium with ambient temperature _T_0, an energy pulse is absorbed on the top surface of the film, resulting in heat diffusion

in the out-of-plane (_z_) direction as well as in the in-plane (_r_) directions. Considering the anisotropic thermal properties, the heat conduction equation for temperature rise _ε__i_ = 

_T_ − _T_0 in layer _i_ is given by $$k_{i - r}\frac{{\partial ^2\varepsilon _i}}{{\partial r^2}} + k_{i - r}\frac{1}{r}\frac{{\partial \varepsilon _i}}{{\partial r}} + k_{i -

z}\frac{{\partial ^2\varepsilon _i}}{{\partial z^2}} = \rho _ic_i\frac{{\partial \varepsilon _i}}{{\partial t}}$$ (1) For the heat absorption on the top surface, $$k_1\frac{\partial

}{{\partial z}}\varepsilon _1\left( {r,z,t} \right) = Q\left( {r,t} \right)$$ (2) where _Q_(_r_, _t_) is the input energy flux, which is spatially and temporally dependent. Here, we adopted

the approach described by Hui et al.43,44 to solve Eqs. (1) and (2) by using Laplace and Hankel transforms: $$V_i\left( {\beta ,z,s} \right) = \mathop {\smallint }\limits_0^\infty

{\mathrm{d}} t\, {\mathrm{exp}}( - st)\mathop {\smallint }\limits_0^{\infty} \varepsilon _i\left( {r,z,t} \right)rJ_0(\beta r){\mathrm{d}}r$$ (4) The problem defined by (1) and (2) can be

recast to obtain the transformed temperature in the spatial and temporal frequency domain (_β_, _s_) as $$\frac{{\mathrm{d}}^2}{{\mathrm{d}}z^2}V_i\left( {\beta ,z,s} \right) - \gamma

_i^2V\left( {\beta ,z,s} \right) = 0$$ (5) $$- k_1\frac{{\mathrm{d}}}{{\mathrm{d}}z}V_i \left( {\beta ,z,s} \right) = Q\left( {\beta ,s} \right)$$ (6) Repeating the solution procedure

described in43,44 yields identical analytical results for _ε__i_, except \(\gamma _i\) in Eq. (5) is defined by $$\gamma _i = \sqrt {\frac{{\rho _ic_i}}{{k_{i - r}}} + \frac{{k_{i -

z}}}{{k_{i - r}}}\beta ^2}$$ (7) This analytical model was validated against the solutions obtained by a finite elements method in ANSYS for the same problem, yielding identical results for

both cases (see Supplementary Note 2). Based on the analytical model, the measured transients are a function of the h-BN out-of-plane (_k_z) and in-plane (_k_r) thermal conductivities,

density, specific heat capacity, thickness of each layer/material, and geometrical and temporal characteristics of the pump pulse. Except for the anisotropic thermal conductivity (_k_z and

_k_r) of h-BN, and the thermal boundary resistance between the Au transducer and h-BN (_TBR_eff), all other parameters are input as fixed values (see Supplementary Note 3). Therefore,

_TBR_eff, _k_z, and _k_r are treated as free variables, adjusted to fit the analytical model results to the measured traces. A least squares algorithm was built for multi-parameter fitting.

The uncertainty (error bar) was determined by individually varying each variable about the solution minima and finding the change in the variable that causes a 5% change in the least squares

value, i.e., the error bar represents a 95% confidence level. Note that _TBR_eff is determined by the ratio of Ti thickness to its fitted thermal conductivity. All fitted results of

_TBR_eff are shown in Supplementary Fig. 3. Supplementary Fig. 4 shows the simulated temperature rise (∆_T_) at the surface of h-BN. The maximum ∆_T_ is ~ 45 K. At 100 ns, ∆_T_ drops to 10 K

and after 1000 ns, ∆_T_ reduces to ~ 1 K. Thus, the fitted h-BN thermal property values approximate the values at ambient temperature. To ensure that the measured thermal conductivity

results are reliable and repeatable, at the beginning of each h-BN sample measurement, we tested an in-house-made reference sample (Au/Ti coated undoped high-purity single crystal silicon)

to make sure the measured silicon thermal conductivity result at room temperature is always equal to the standard value, 150 W/mK45,46. SENSITIVITY ANALYSIS The sensitivity of the

temperature decay curve (_T_) to a parameter, _x_0, which is either thermal conductivity or thermal boundary resistance, is defined as:28 $$S_{x_0} = \frac{{\partial \left( {{\mathrm{ln}}T}

\right)}}{\partial \left( {{\mathrm{ln}}x_0} \right)}$$ (8) When _x_0 changes by ±10% within the timescale of interest: $$S_{x_0} = \frac{\partial \left( {{\mathrm{ln}}T} \right)}{\partial

\left( {{\mathrm{ln}}x_0} \right)} \approx \frac{{\mathrm{ln}}\left( {T_{1.1x_0}} \right) - {\mathrm{ln}}\left( {T_{0.9x_0}} \right)}{{\mathrm{ln}}\left( {1.1x_0} \right) -

{\mathrm{ln}}\left( {0.9x_0} \right)}$$ (9) Figure 2d shows an example of the sensitivity to _k_r, _k_z and _TBR_eff for a h-BN sample (the properties are taken as _k_r = 400 W m−1 K−1, _k_z

 = 4 W m−1 K−1, _C_p = 740 J kg−1 K−1 and TBReff = 50 m2 K GW−1, which are typical values for h-BN4,42). FIRST PRINCIPLES THERMAL CONDUCTIVITY CALCULATIONS Calculations of the thermal

conductivity of h-BN are derived from Peierls–Boltzmann phonon transport32,47,48 with interatomic force constants (harmonic and third-order anharmonic) from DFT49,50,51 as implemented by the

plane-wave Quantum Espresso package51 within the local density approximation using norm-conserving pseudopotentials. Electronic structure and relaxation (12 × 12 × 8 integration grid and

110 Ryd plane-wave energy cutoff) gave lattice parameters, _a_ = 2.478 Å and _c_ = 6.425 Å4, somewhat smaller than measurements52. Density functional perturbation theory50 (8 × 8 × 6

integration grid) was used to calculate harmonic force constants and long range Coulomb corrections. Γ-point-only electronic structure calculations (200 atom supercells, interactions

restricted to 2.8 Å within the plane and 4.2 Å for neighboring layers) were used to determine third-order anharmonic force constants for constructing three-phonon matrix elements4. Thermal

resistance from three-phonon interactions32,47 and phonon–isotope scattering11,53,54 is determined from quantum perturbation theory. More details specific to the DFT calculations and phonon

properties (e.g., dispersions and scattering rates) are given in4. DATA AVAILABILITY The data that support the plots and findings of this paper are available at

https://doi.org/10.5523/bris.16v9rfpzb3pl221yzel7x5u5ce. REFERENCES * Watanabe, K., Taniguchi, T., Niiyama, T., Miya, K. & Taniguchi, M. Far-ultraviolet plane-emission handheld device

based on hexagonal boron nitride. _Nat. Photonics_ 3, 591–594 (2009). Article  ADS  Google Scholar  * Li, P. N. et al. Hyperbolic phonon-polaritons in boron nitride for near-field optical

imaging and focusing. _Nat. Commun._ 6, 7507 (2015). Article  Google Scholar  * Izyumskaya, N. et al. Recent development of boron nitride towards electronic applications. _Adv. Electron.

Mater._ 3, 1600485 (2017). Article  Google Scholar  * Jiang, P. Q., Qian, X., Yang, R. G. & Lindsay, L. Anisotropic thermal transport in bulk hexagonal boron nitride. _Phys. Rev. Mater._

2, 064005 (2018). Article  Google Scholar  * Akinwande, D., Petrone, N. & Hone, J. Two-dimensional flexible nanoelectronics. _Nat. Commun._ 5, 5678 (2014). Article  ADS  Google Scholar

  * Zhang, Z. W., Hu, S. Q., Chen, J. & Li, B. W. Hexagonal boron nitride: a promising substrate for graphene with high heat dissipation. _Nanotechnology_ 28, 225704 (2017). Article  ADS

  Google Scholar  * Yuan, C. et al. Thermal conductivity of polymer-based composites with magnetic aligned hexagonal boron nitride platelets. _Acs Appl. Mater. Inter._ 7, 13000–13006 (2015).

Article  Google Scholar  * Xie, B. et al. Targeting cooling for quantum dots in white QDs-LEDs by hexagonal boron nitride platelets with electrostatic bonding. _Adv. Funct. Mater._ 28,

1801407 (2018). Article  Google Scholar  * Simpson, A. & Stuckes, A. D. Thermal conductivity of highly orientated pyrolytic boron nitride. _J. Phys. Part C. Solid_ 4, 1710–1718 (1971).

Article  ADS  Google Scholar  * Sichel, E. K., Miller, R. E., Abrahams, M. S. & Buiocchi, C. J. Heat-capacity and thermal-conductivity of hexagonal pyrolytic boron-nitride. _Phys. Rev.

B_ 13, 4607–4611 (1976). Article  ADS  Google Scholar  * Lindsay, L., Broido, D. A. & Reinecke, T. L. Phonon-isotope scattering and thermal conductivity in materials with a large isotope

effect: a first-principles study. _Phys. Rev. B_ 88, 144306 (2013). Article  ADS  Google Scholar  * Inyushkin, A. V., Taldenkov, A. N., Gibin, A. M., Gusev, A. V. & Pohl, H. J. On the

isotope effect in thermal conductivity of silicon. _Phys. Status Solidi C._ 1, 2995–2998 (2004). Article  ADS  Google Scholar  * Ozhogin, V. I. et al. Isotope effect in the thermal

conductivity of germanium single crystals. _J. Exp. Theor. Phys._ 63, 490–494 (1996). Article  Google Scholar  * Inyushkin, V. et al. Thermal conductivity of isotopically enriched.

(GaAs)-Ga-71 crystal. _Semicond. Sci. Tech._ 18, 685–688 (2003). Article  ADS  Google Scholar  * Anthony, T. R. et al. Thermal-diffusivity of isotopically enriched C-12 diamond. _Phys. Rev.

B_ 42, 1104–1111 (1990). Article  ADS  Google Scholar  * Chen, S. S. et al. Thermal conductivity of isotopically modified graphene. _Nat. Mater._ 11, 203–207 (2012). Article  ADS  Google

Scholar  * Chang, C. W. et al. Isotope effect on the thermal conductivity of boron nitride nanotubes. _Phys. Rev. Lett_. 97, 085901 (2006). * Wei, L. H., Kuo, P. K., Thomas, R. L., Anthony,

T. R. & Banholzer, W. F. Thermal-conductivity of isotopically modified single-crystal diamond. _Phys. Rev. Lett._ 70, 3764–3767 (1993). Article  ADS  Google Scholar  * Morelli, D. T.,

Heremans, J. P. & Slack, G. A. Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. _Phys. Rev. B_ 66, 195304 (2002). Article

  ADS  Google Scholar  * Lindsay, L., Broido, D. A. & Mingo, N. Flexural phonons and thermal transport in multilayer graphene and graphite. _Phys. Rev. B_ 83, 235428 (2011). Article  ADS

  Google Scholar  * Fugallo, G. et al. Thermal conductivity of graphene and graphite: collective excitations and mean free paths. _Nano Lett._ 14, 6109–6114 (2014). Article  ADS  Google

Scholar  * Lindroth, D. O. & Erhart, P. Thermal transport in van der Waals solids from first-principles calculations. _Phys. Rev. B_ 94, 115205 (2016). Article  ADS  Google Scholar  *

Vuong, T. Q. P. et al. Isotope engineering of van der Waals interactions in hexagonal boron nitride. _Nat. Mater._ 17, 152–158 (2018). Article  ADS  Google Scholar  * Giles, A. J. et al.

Ultralow-loss polaritons in isotopically pure boron nitride. _Nat. Mater._ 17, 134–139 (2018). Article  ADS  Google Scholar  * Liu, S. et al. Single crystal growth of millimeter-sized

monoisotopic hexagonal boron nitride. _Chem. Mater._ 30, 6222–6225 (2018). Article  Google Scholar  * Shtukenberg, A. G. et al. Illusory spirals and loops in crystal growth. _Proc. Natl

Acad. Sci. USA_ 110, 17195–17198 (2013). Article  ADS  Google Scholar  * Goodson, K. E., Kading, O. W., Rosler, M. & Zachai, R. Experimental investigation of thermal conduction normal to

diamond-silicon boundaries. _J. Appl. Phys._ 77, 1385–1392 (1995). Article  ADS  Google Scholar  * Garrelts, R., Marconnet, A. & Xu, X. F. Assessment of thermal properties via

nanosecond thermoreflectance method. _Nanosc. Microsc. Therm._ 19, 245–257 (2015). Article  Google Scholar  * Anufriev, R., Ramiere, A., Maire, J. & Nomura, M. Heat guiding and focusing

using ballistic phonon transport in phononic nanostructures. _Nat. Commun._ 8, 15505 (2017). Article  ADS  Google Scholar  * Katre, A., Carrete, J., Dongre, B., Madsen, G. K. H. & Mingo,

N. Exceptionally strong phonon scattering by B substitution in cubic SiC. _Phys. Rev. Lett._ 119, 075902 (2017). Article  ADS  Google Scholar  * Polanco, C. A. & Lindsay, L. Thermal

conductivity of InN with point defects from first principles. _Phys. Rev. B_ 98, 014306 (2018). Article  ADS  Google Scholar  * Ziman, J. M. _Electrons and Phonons; The Theory of Transport

Phenomena in Solids_ (Clarendon Press, Oxford, 1960). * Lindsay, L. & Broido, D. A. Three-phonon phase space and lattice thermal conductivity in semiconductors. _J. Phys.-Condens. Mat._

20, 165209 (2008). Article  ADS  Google Scholar  * Ma, Y. G., Liu, Y. C., Raza, M., Wang, Y. D. & He, S. L. Experimental demonstration of a multiphysics cloak: manipulating heat flux and

electric current simultaneously. _Phys. Rev. Lett._ 113, 205501 (2014). Article  ADS  Google Scholar  * Ma, Y. G., Lan, L., Jiang, W., Sun, F. & He, S. L. A transient thermal cloak

experimentally realized through a rescaled diffusion equation with anisotropic thermal diffusivity. _Npg Asia Mater._ 5, e73 (2013). Article  Google Scholar  * Li, J. Y., Gao, Y. &

Huang, J. P. A bifunctional cloak using transformation media. _J. Appl. Phys._ 108, 074504 (2010). Article  ADS  Google Scholar  * Narayana, S. & Sato, Y. Heat flux manipulation with

engineered thermal materials. _Phys. Rev. Lett._ 108, 214303 (2012). Article  ADS  Google Scholar  * Mateti, S. et al. Bulk hexagonal boron nitride with a quasi-isotropic thermal

conductivity. _Adv. Funct. Mater._ 28, 1707556 (2018). Article  Google Scholar  * Cahill, D. G. et al. Nanoscale thermal transport. _J. Appl. Phys._ 93, 793–818 (2003). Article  ADS  Google

Scholar  * Koh, Y. K., Cao, Y., Cahill, D. G. & Jena, D. Heat-transport mechanisms in superlattices. _Adv. Funct. Mater._ 19, 610–615 (2009). Article  Google Scholar  * Feser, J. P.

& Cahill, D. G. Probing anisotropic heat transport using time-domain thermoreflectance with offset laser spots. _Rev. Sci. Instrum._ 83, 104901 (2012). Article  ADS  Google Scholar  *

Jiang, P. Q., Qian, X. & Yang, R. G. Time-domain thermoreflectance (TDTR) measurements of anisotropic thermal conductivity using a variable spot size approach. _Rev. Sci. Instrum._ 88,

074901 (2017). Article  ADS  Google Scholar  * Hui, P. & Tan, H. S. A transmission-line theory for heat-conduction in multilayer thin-films. _IEEE T. Compon. Pack. B_ 17, 426–434 (1994).

Article  Google Scholar  * Chen, G. & Hui, P. Pulsed photothermal modeling of composite samples based on transmission-line theory of heat conduction. _Thin Solid Films_ 339, 58–67

(1999). Article  ADS  Google Scholar  * Glassbrenner, C. J. & Slack, G. A. Thermal conductivity of silicon and germanium from 3 degrees K to melting point. _Phys. Rev._ 134, A1058

(1964). Article  ADS  Google Scholar  * Schmidt, A. J., Chen, X. Y. & Chen, G. Pulse accumulation, radial heat conduction, and anisotropic thermal conductivity in pump-probe transient

thermoreflectance. _Rev. Sci. Instrum._ 79, 114902 (2008). Article  ADS  Google Scholar  * Srivastava, G. P. _The Physics of Phonons_ (A. Hilger, Bristol, Philadelphia, 1990). * Lindsay, L.

First principles peierls-boltzmann phonon thermal transport: a topical review. _Nanosc. Microsc. Therm._ 20, 67–84 (2016). Article  Google Scholar  * Hohenberg, P. & Kohn, W.

Inhomogeneous electron gas. _Phys. Rev. B_ 136, B864 (1964). Article  ADS  MathSciNet  Google Scholar  * Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related

crystal properties from density-functional perturbation theory. _Rev. Mod. Phys._ 73, 515–562 (2001). Article  ADS  Google Scholar  * Giannozzi, P. et al. Quantum Espresso: a modular and

open-source software project for quantum simulations of materials. _J. Phys.-Condens. Mat._ 21, 395502 (2009). Article  Google Scholar  * Paszkowicz, W., Pelka, J. B., Knapp, M., Szyszko, T.

& Podsiadlo, S. Lattice parameters and anisotropic thermal expansion of hexagonal boron nitride in the 10–297.5 K temperature range. _Appl. Phys. A_ 75, 431–435 (2002). Article  ADS 

Google Scholar  * Tamura, S. Isotope scattering of large-wave-vector phonons in GaAs and InSb - deformation-dipole and overlap-shell models. _Phys. Rev. B_ 30, 849–854 (1984). Article  ADS 

Google Scholar  * Lindsay, L. & Broido, D. A. Enhanced thermal conductivity and isotope effect in single-layer hexagonal boron nitride. _Phys. Rev. B_ 84, 155421 (2011). Article  ADS 

Google Scholar  Download references ACKNOWLEDGEMENTS C.Y., J.W.P., and M.K. acknowledge support from the Engineering and Physics Science Research Council Grant EP/P00945X/1, J.L., S.L., and

J.H.E. from the Materials Engineering and Processing program of the National Science Foundation, award number CMMI 1538127. First principles calculations were supported by the U.S.

Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. We gratefully acknowledge M. Singh for the help of samples preparation for TTR

and TEM analysis, C. Jones for support with EBSD, and W. Waller for multi-parameter fitting programming and H. Chandrasekar and R. Baranyai for fruitful discussions. AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Center for Device Thermography and Reliability (CDTR), H. H. Wills Physics Laboratory, University of Bristol, BS8 1TL, Bristol, UK Chao Yuan, James W. Pomeroy 

& Martin Kuball * Tim Taylor Department of Chemical Engineering, Kansas State University, Manhattan, KS, 66506, USA Jiahan Li, Song Liu & James H. Edgar * Materials Science and

Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA Lucas Lindsay * Materials and Devices for Energy and Communications Group, H. H. Wills Physics Laboratory,

University of Bristol, BS8 1TL, Bristol, UK David Cherns Authors * Chao Yuan View author publications You can also search for this author inPubMed Google Scholar * Jiahan Li View author

publications You can also search for this author inPubMed Google Scholar * Lucas Lindsay View author publications You can also search for this author inPubMed Google Scholar * David Cherns

View author publications You can also search for this author inPubMed Google Scholar * James W. Pomeroy View author publications You can also search for this author inPubMed Google Scholar *

Song Liu View author publications You can also search for this author inPubMed Google Scholar * James H. Edgar View author publications You can also search for this author inPubMed Google

Scholar * Martin Kuball View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS J.L. and S.L. synthesized the h-BN samples under the direction of

J.H.E.; C.Y. performed the Raman, SEM, EBSD, and TTR measurements under direction of M.K.; C.Y. and J.W.P. performed the TTR data analysis. D.C. performed the TEM measurements and analysis.

L.L. performed the first principles thermal conductivity calculations. All authors discussed results at all stages and participated in the development of the manuscript. CORRESPONDING

AUTHORS Correspondence to Chao Yuan or Martin Kuball. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN

ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format,

as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third

party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yuan, C., Li, J., Lindsay, L. _et

al._ Modulating the thermal conductivity in hexagonal boron nitride via controlled boron isotope concentration. _Commun Phys_ 2, 43 (2019). https://doi.org/10.1038/s42005-019-0145-5 Download

citation * Received: 18 December 2018 * Accepted: 08 March 2019 * Published: 02 May 2019 * DOI: https://doi.org/10.1038/s42005-019-0145-5 SHARE THIS ARTICLE Anyone you share the following

link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature

SharedIt content-sharing initiative