Increased prediction accuracy using combined genomic information and physiological traits in a soft wheat panel evaluated in multi-environments

ABSTRACT An integration of field-based phenotypic and genomic data can potentially increase the genetic gain in wheat breeding for complex traits such as grain and biomass yield. To validate

this hypothesis in empirical field experiments, we compared the prediction accuracy between multi-kernel physiological and genomic best linear unbiased prediction (BLUP) model to a

single-kernel physiological or genomic BLUP model for grain yield (GY) using a soft wheat population that was evaluated in four environments. The physiological data including canopy

temperature (CT), SPAD chlorophyll content (SPAD), membrane thermostability (MT), rate of senescence (RS), stay green trait (SGT), and NDVI values were collected at four environments (2016,

2017, and 2018 at Citra, FL; 2017 at Quincy, FL). Using a genotyping-by-sequencing (GBS) approach, a total of 19,353 SNPs were generated and used to estimate prediction model accuracy.

Prediction accuracies of grain yield evaluated in four environments improved when physiological traits and/or interaction effects (genotype × environment or physiology × environment) were

included in the model compared to models with only genomic data. The proposed multi-kernel models that combined physiological and genomic data showed 35 to 169% increase in prediction

accuracy compared to models with only genomic data included when heading date was used as a covariate. In general, higher response to selection was captured by the model combing effects of

physiological and genotype × environment interaction compared to other models. The results of this study support the integration of field-based physiological data into GY prediction to

improve genetic gain from selection in soft wheat under a multi-environment context. SIMILAR CONTENT BEING VIEWED BY OTHERS EXPLORING THE GENOTYPE-ENVIRONMENT INTERACTION OF BREAD WHEAT IN

AMBIENT AND HIGH-TEMPERATURE PLANTING CONDITIONS: A RIGOROUS INVESTIGATION Article Open access 29 January 2024 WEIGHTED KERNELS IMPROVE MULTI-ENVIRONMENT GENOMIC PREDICTION Article Open

access 15 December 2022 GENOMIC PREDICTION IN MULTI-ENVIRONMENT TRIALS IN MAIZE USING STATISTICAL AND MACHINE LEARNING METHODS Article Open access 11 January 2024 INTRODUCTION Genomic

selection (GS) that predicts genomic estimated breeding value (GEBV) of individuals using genome-wide molecular markers1 has proven to be a promising technique for accelerated plant

breeding. Studies have shown that breeding programs that incorporated GS often resulted in a near two-fold genetic gain compared to standard phenotypic selection2,3. The rapid development of

high-throughput phenotyping in multi-environment field trials and multi-variate statistical tools also contributed to improved accuracy of prediction and selection of candidate lines4,5. In

GS, a training population (TP) is established to estimate marker effects, for which phenotypic (e.g. grain yield) and genotypic (e.g. DNA marker) data are available. The estimated marker

effects from the TP are then used to predict phenotypes in a new set of germplasm, called breeding population (BP) or validation population (VP), that only need to be genotyped with DNA

markers. A breeding value will be predicted for all the individuals in BP based on the composition of markers being scored. Individuals with high GEBV will be selected prior to being

evaluated in field experiments, therefore, increasing selection population size and accelerating the selection-evaluation cycles in plant breeding6,7. GS is particularly valuable for many

quantitative traits such as grain yield and biomass partitioning traits that are affected by large numbers of small-effect genes8. Therefore, the selection of the complex traits using

genome-wide markers can be more effective than marker-assisted selection using a few markers. The importance of exploiting multi-environment information has been recognized in plant breeding

to overcome genotype × environment interaction (GE). Burgueño _et al_.9 evaluated three crops (potato [_Solanum tuberosum_ L.], maize [_Zea mays_ L.], and wheat [_Triticum aestivum_ L.]) in

a multi-environment trial and concluded that the predictability of the model increased up to 6% when GE was included in a factor analytic model. Another study in maize (_Zea mays_ L.)

showed similar results when GE effect was modeled to account for the heterogeneity and correlation between environments10. In recent years, combining phenotypic and genomic data in

prediction studies have emerged as a useful technology for improving breeding efficiency. Montesinos-López _et al_.11 used hundreds of reflectance data from hyperspectral cameras to predict

wheat grain yield. They found that using all reflectance data simultaneously increased prediction accuracy than using a single vegetation index alone. In another study, Aguate _et al_.12

indicated that integrating all hyperspectral wavelengths using ordinary least squares, partial least squares, and Bayesian shrinkage resulted in higher prediction accuracy than using

individual vegetation indices in maize. Pérez-Rodríguez _et al_.13, Cuevas _et al_.14, and Crain _et al_.15 reported improvement in prediction accuracies using a multi-environment model

relative to a single-environment model. Montesinos-López _et al_.16 also observed that prediction models incorporated hyperspectral data and spectrum by environment interaction terms were

more accurate than those did not. In their study, a Bayesian functional regression analysis using all hyperspectral bands was integrated in order to address the high dimensionality of

hyperspectral data. Krause _et al_.17 used genomic marker-, pedigree-, and hyperspectral reflectance-derived relationship matrices to construct genomic-enabled BLUP models to evaluate the

genetic main effects (G) and GE interactions across environments in a wheat breeding program and showed the highest prediction accuracies when combining marker/pedigree information with

hyperspectral reflectance phenotypes. Physiological traits including chlorophyll content (SPAD-based), canopy temperature (CT), membrane thermostability (MT), and normalized difference

vegetation index (NDVI) have shown significant association with grain yield in wheat, especially under stressed environments18,19,20,21,22,23. However, studies on prediction of grain yield

using field-based physiological traits are limited. Weber _et al_.24 showed that, in maize, introducing spectral reflectance measurements at anthesis and milk-grain stage into a partial

least square regression (PLSR) model accounted for 23% and 40% of the genotypic variation in grain yield, respectively. Their PLSR models explained a higher proportion of the genetic

variation in grain yield under drought stress than that under well-watered conditions. The prediction of grain yield could be potentially more accurate when a multi-kernel model is

implemented in GS, in which multi-traits data and dense molecular marker information are converted into a set of distance matrices and formulated in a semi-parametric Reproducing Kernel

Hilbert Space25,26. Pérez _et al_.27 applied a Bayesian-based prediction model utilizing both molecular markers and pedigree information and extended it to a multi-kernel prediction model

suitable for combining multiple omic data28. This approach was proved to increase prediction accuracies in maize and wheat14,16,17,29. Therefore, the objectives of this study were to: 1)

propose models using genomic and field-based physiological data to predict the grain yield in a soft facultative wheat panel, 2) compare the prediction accuracies of the model that combined

field-based physiological traits with genomic data under a multi-environment context to the model that was built on either physiological traits or genomic data, and 3) rank the importance of

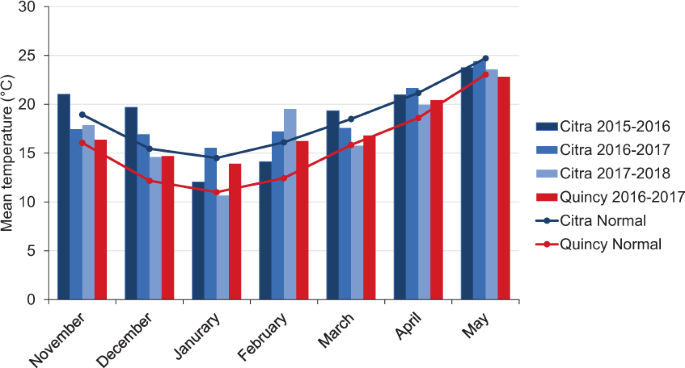
contribution by different physiological traits to grain yield. RESULTS LOCATION AND WEATHER In general, Quincy had lower temperatures than Citra from November of first year to May of second

year (Fig. 1). However, the differences in temperature were smaller from March to May compared to other months. Unusually high precipitation occurred during January in Quincy 2017, and

April and May in Citra 2018. Low precipitation was observed in March at both locations throughout the experimental period (Fig. 2). Additionally, the two locations had different soil types,

where Citra had a sandy soil profile compared to a heavier soil texture in Quincy. DESCRIPTIVE STATISTICS The same soft wheat panel was evaluated at four environments: Citra 2016, Citra

2017, Citra 2018, and Quincy 2017. Quincy 2017 and Citra 2018 showed higher GY and earlier days to heading (DTH) than Citra 2016 and 2017 (Table 1, Fig. 3). The SPAD and MT data were not

taken in Citra 2018 and Citra 2016, respectively. The LSmeans of SPAD, MT, and NDVI measured at six time points were similar among environments. In Citra 2016, CT was the lowest compared to

other environments. For RS, Citra 2018 had the lowest value while Citra 2016 had the highest value. In Citra 2016, SG value was highest compared to other environments. Overall, physiological

traits in Citra 2016 showed higher variability than other environments (Figs. 3, S1). Broad sense heritability estimates for GY were between 0.2 and 0.41. For DTH, heritabilities were

generally high between 0.69 and 0.95. Quincy 2017 showed the lowest heritability (0.24) while Citra 2016 was the highest (0.74) for SPAD. Heritabilities of MT highly varied among

environments from 0.19 to 0.75. The NDVI values showed much lower heritability in Citra 2016 than other environments especially for NDVI_1, NDVI_2, NDVI_3, and NDVI_4. For RS, the

heritabilities ranged from 0.43 to 0.87 among environments. Heritabilities of SG varied from 0.14 to 0.96 among environments. Correlations between physiological traits and GY also highly

varied among environments (Table 1). Heading date significantly correlated with GY in Citra 2017 and Citra 2018 but was not correlated with GY in Citra 2016 and Quincy 2017. In the three

environments, SPAD were positively correlated with GY (_p_ = 0.38, 0.14, 0.27 at Citra 2016, Citra 2017, and Quincy 2017, respectively). In Citra 2017 and Quincy 2017, MT values were

positively correlated with GY (_p_ = 0.31 and 0.2 at Citra 2017 and Quincy 2017, respectively). The first three NDVI measurements (NDVI_1, NDVI_2, and NDVI_3) were negatively correlated with

GY (_p_ from −0.45 to −0.17) except for Quincy 2017 (_p_ from 0.06 to 0.14). NDVI_5 and NDVI_6 were negatively correlated with GY in Citra 2017 and Citra 2018 (_p_ from −0.43 to −0.42 and

−0.44 to −0.29 at Citra 2017 and Citra 2018, respectively). Citra 2017 and Citra 2018 showed negative correlations between RS and GY (_p_ = −0.44 and −0.4 at Citra 2017 and Citra 2018,

respectively). For SG, Citra 2017 showed positive correlation with GY and Citra 2018 had negative correlation (_p_ = 0.18 and −0.27 at Citra 2017 and Citra 2018, respectively). MODEL

PREDICTION ACCURACY To determine the population structure in the soft wheat panel, 242 lines were clustered into 10 groups using the _DAPC_ algorithm (Fig. 4). Each sub-group consisted of 21

to 35 lines which were then randomly assigned to five different folds for cross validation analysis. When DTH was used as a covariate, prediction accuracies of models using model (3) (_G_

only) ranged from 0.18 (Quincy 2017) to 0.42 (Citra 2017) (Fig. 5a). When model (6) (_P_ only) was used, all environments showed higher prediction accuracies (from 0.18 to 0.59) than model

(3) except for Citra 2018. Model (4) including _G_ and _G_ × _E_ interaction showed higher prediction accuracies than model (3) except for Citra 2016. Model (5) including _G_ and _P_ × _E_

showed the highest prediction accuracies in Citra 2018 (0.48) among six models. Model (7) using _P_ and _P_ × _E_ had the highest prediction accuracies in Citra 2016 (0.55) and Quincy 2017

(0.55). Model (8) using _P_ and _G_ × _E_ had the highest prediction accuracy in Citra 2017 (0.75). When DTH was not used a covariate, all environments showed similar patterns as models with

DTH corrected (Fig. 5b). However, the prediction accuracies increased across environments except for models with _G_ or _G_ + _G_ × _E_. Whether DTH being corrected or not, models

incorporating physiological traits (_P_) and environmental effects (_E_) performed better than _G_ or _P_ only, with exceptions when comparing model (6) and model (8) at Quincy 2017 and

Citra 2016. RESPONSE TO SELECTION When comparing the response to selection (RTS) based on each model in each environment, models considering both _P_ and _G_ × _E_ showed generally higher

performance (116, 410, and 221 at Citra 2016, Citra 2017, and Citra 2018, respectively) with DTH correction (Fig. 6) than other models. In environments where GY showed relatively low

heritability (i.e. Citra 2016 and Quincy 2017), models involved with _P_ or _P_ × _E_ had higher RTS compared to models with _G_ or _G_ × _E_. On the contrary, in environments with higher

heritability for GY (i.e. Citra 2017 and Citra 2018), models included _G_ or _G_ × _E_ showed higher RTS than models included _P_ or _P_ × _E_. In Citra 2018, models of _P_ and _P_ + _P_ ×

_E_ had the lowest RS (25 and 22, respectively) among all environments. When DTH was not used as the covariate for GY, a similar pattern but generally higher RTS was observed for all the

environments (Fig. 6b). Models (8) which involving _P_ and _G_ × _E_ showed the highest RTS at Citra 2017 and Citra 2018 (506 and 274, respectively), followed by model (5) involving _G_ and

_P_ × _E_ (491 and 260, respectively). Model (4) at Quincy 2017 and model (6) at Citra 2018, formulated as _G_ + _G_ × _E_ and _P_, respectively, had the lowest RTS (22 and 86, respectively)

across all environments. MULTI-VARIATE ANALYSIS FOR PHYSIOLOGICAL TRAITS The relative importance of physiological traits contributing to GY was analyzed using machine learning based

clustering method. Data from Citra 2017 and Quincy 2017 was selected for this analysis since all physiological traits were available in these two environments. The cross-validation results

(alpha = 1; lambda = 10.3) suggested using a least absolute shrinkage and selection operator (LASSO) model to estimate the coefficients of each variables. When DTH was not included as a

covariate, the dominant contributor to GY in Citra 2017 was NDVI_2 followed by NDVI_3 and CT. The relative contribution of top three traits was scored as 100, 65, and 61, respectively (Fig. 

7a). For Quincy 2017, CT was the dominant contributor to GY followed by SPAD (90), NDVI_1 (74), and NDVI_3 (64) (Fig. 7b). In both environments, NDVI_4 and NDVI_5 were not very important.

When DTH was not included as a covariate, the overall rank of physiological traits was similar in each environment compared to analysis with DTH (Figs. 7c,d). In Citra 2017, RS became the

second most important contributor to GY when DTH was included. In Quincy 2017, SG rose to be the most important contributor to GY, and RS also ranked higher compared to analysis with DTH

included. DISCUSSION MODEL PREDICTION ACCURACY Our study found that, considering both field-based physiological measurements, genomic information, and genotype × environment (or physiology ×

environment) in a multi-kernel BLUP model can significantly improve prediction accuracy for GY. Physiological traits such as SPAD, CT, MT, and NDVI measured between heading and maturity

stage are reported to be effective to predict GY18,19,20,21,22,23. When physiological traits were added to multi-kernel models (5, 7, and 8), the prediction accuracies were similar to

previous reports17,30. In addition, the prediction accuracies in the current study are also site-specific in terms of magnitude of differences between _G_ and _G_ + _P_ models. However, in

their studies, thermo- and spectral camera-based imaging analysis was implemented to measure CT and vegetation indices which had a higher heritability than the physiological traits measured

in this study. Prediction models using a multi-variate set of phenotypic data has proven to enhance the prediction accuracy compared to using a single phenotypic trait16,17. In our study,

the prediction accuracies using only _P_ matrices are close to other models in several environments. The addition of genomic information and interactions in models improved prediction

accuracies only in a marginal scale in those environments. The missing SPAD measurement in Citra 2018 could contribute to a much lower prediction accuracy using only _P_ matrix. This result

is consistent to Krause _et al_.17 and Montesinos-López _et al_.11. In this study, when DTH is corrected in estimating GY, prediction accuracies for the models involving only _G_ matrices

were similar to models without DTH correction. However, when _P_ matrices were included in these models, prediction accuracies were generally reduced in all environments except for Citra

2016 and model (7) in Quincy 2017, which agrees with Krause _et al_.17 and Rutkoski _et al_.30. However, the magnitudes of differences between models with and without DTH correction were

marginal except for Citra 2018. This is probably due to missing data on SPAD in Citra 2018. This again indicated that SPAD plays an important role in contributing to GY. Correcting GY for

DTH can avoid indirect selection on maturity traits. Our results confirmed that variation in physiological traits such as NDVI values is correlated with maturity differences among lines.

Thus, the prediction accuracies derived after DTH correction are more informative. RESPONSE TO SELECTION For a plant breeding program, it is a common practice to evaluate the genetic gain

based on response to selection31. In this study, we calculated RTS based on GEBV from the proposed models for each environment. In general, environments with higher heritability for GY had

higher RTS. Model (8) (_P_ and _G_ × _E_) and model (4) (_G_ and _G_ × _E_) showed to be superior than other models in environments where GY had high heritability. However, in a low

heritability environment such as Citra 2016 or Quincy 2017 in our study, selection using physiological traits (_P_ or _P_ × _E_) could perform better than GS (_G_ or _G_ × _E_). Crain _et

al_.15 also found that physiological traits can be used to improve model performance over GS models alone in different environments. However, high-throughput phenotyping techniques were used

to measure physiological traits such as NDVI and CT in their study. Ultimately, based on our results, the potential of increasing genetic gains for GY can be achieved by applying a

multi-kernel model implemented with information of physiological traits. MULTI-VARIATE ANALYSIS FOR PHYSIOLOGICAL TRAITS Because the same set of physiological traits were measured in Citra

2017 and Quincy 2017, data from these two environments were used to investigate the importance of physiological traits contributing to GY. The machine learning-based clustering analysis

indicated that importance of physiological traits to GY are environment specific. However, NDVI_3 that was measured at the end of milk stage (Zadoks 79) and CT were ranked on the top in both

environments. Previous studies showed milk-grain or milk-dough stages were critical in determining the grain yield in various environments32,33,34. High throughput phenotyping methods such

as satellite imaging, UAV spectral imaging and proximal phenotyping are advancing at a rapid pace35,36,37,38. It is now possible to collect vegetative indices across all growth stages. The

results from the clustering analysis suggest that, phenotyping plants during milk-grain stages could improve the prediction accuracy on GY. The impact of canopy temperature on grain yield

was also well documented19,35,39. Cooler CT is associated with higher stomatal conductance and better hydration status under drought condition, in return it results in a higher yield40,41.

Therefore, using thermo-camera to collect CT data during grain filling stage could also improve the prediction accuracy on GY. For Quincy 2017, SPAD was the top contributor to GY. In

previous studies, higher chlorophyll content was associated with greater grain yield especially under drought conditions42,43,44. There was a drought period during March 2017, which could

result in a lower yield for the genotypes that were vulnerable to the drought conditions. Therefore, SPAD measurement played a more important role in Quincy 2017 than that in Citra 2017.

When GY was not corrected for DTH, the overall pattern remained the same for each environment except for a higher rank of RS and SG on both lists. Since RS and SG are directly correlated

with NDVI values and maturity, they would be inherently correlated with phenology. Therefore, the attention on RS and SG should be weighed carefully when a diverse panel of germplasm is

evaluated. CONCLUSIONS In this study, we combined field-based phenotyping and genomic information to predict grain yield using multi-kernel models in the soft wheat panel. The multi-kernel

models and single-kernel model using physiological trait information provided better prediction accuracies than the single-kernel model using genomic data only. Therefore, applying high

throughput phenotyping on SPAD, CT, MT, and NDVI during milk-grain stages could potentially accelerate selection and advancing germplasm in wheat. The multi-dimensional aerial- or

ground-based high throughout phenotyping information could in turn argument the selection of traits used to predict GY. Although the classification of time-point when these traits are

collected is probably specific to environments and genetic backgrounds of the lines, the importance of certain period during growth stages could be easily evaluated using the same

methodology proposed in this study. Our study provides baseline information on using physiological traits to predict grain yield in wheat in a multi-environment context. MATERIALS AND

METHODS PLANT MATERIALS AND EXPERIMENTAL DESIGN A diversity panel of 242 soft facultative wheat with relatively low vernalization requirement for most of the genotypes was used in the

present study. These lines were released from public and private soft wheat breeding programs in the southern and southeastern U.S. to represents a broad genetic base of US soft wheat. The

panel was phenotyped for both physiological and yield related traits at the Plant Science Research and Education Unit (PSREU) in Citra, Florida from 2016 to 2018 and at the North Florida

Research and Education Center (NFREC) in Quincy, Florida in 2017. All field experiments were planted in an un-replicated randomized augmented design with three repeated checks (“AGS 2000”,

“SS8641”, and “Jamestown”). Each line was planted in six row plots (3 m × 1.5 m) at the rate of 100 kg h-1. Pesticides were sprayed for management of local diseases, weeds, and insects as

needed. Fertilizer and irrigation were applied based on plant growth stages and field moisture condition to avoid any water or nutrient deficiency, respectively. Planting dates were delayed

to late December to increase post-anthesis heat stress conditions. Weather data, including average temperature (60 cm above canopy) and precipitation, were retrieved from Florida Automated

Weather Network (FAWN) and the National Oceanic and Atmosphere Administration (NOAA) for each environment (Figs. 1 and 2). FIELD DATA COLLECTION AND CALCULATIONS Physiological traits

including SPAD, CT, MT, NDVI values at six time points (Zadoks stages 65, 72, 79, 86, 93 and 100, respectively), RS, and SG were measured from each plot in each experiment. SPAD chlorophyll

content of flag leaf was measured when plants reached early milk stage (Zadoks stage 72, or seven days after anthesis) using a handheld chlorophyll meter (Minolta SPAD-502 Spectrum

Technologies Inc., Plainfield, IL, US). CT was recorded three times during grain filling using a handheld infrared thermometer (Fluke 572-2 IR thermometer, Fluke Corporation, Everett WA)

during cloudless, sunny day when the temperature reached daily high. To determine MT, flag leaves were collected from ten random main stem at early milk stage (Zadoks stage 72).

One-centimeter diameter leaf disks were collected from the middle section of the ten leaf blades using a paper puncher and placed in glass vial containing 20 ml deionized water. The leaf

samples were then processed following Ibrahim & Quick45 and MT was expressed in percentage units as the reciprocal of relative electrolyte leakage measured by conductometer (Thermo

Scientific Orion Star A212) followed by autoclaving the vials (0.10 MPa pressure, 121 °C for 15 min) to release all the electrolytes from plant tissue.

$${\rm{MT}}=(1\mbox{--}{{\rm{T}}}_{1}/{{\rm{T}}}_{2})\times 100$$ where T1 is the conductivity reading after heat treatment, and T2 is the conductivity reading after autoclaving. All NDVI

values were measured using a GreenSeeker sensor (Trimble Navigation, Ltd., Sunny Vale, CA, USA). The GreenSeeker was held 30 cm above the canopy and scan through the center of each plot. An

averaged reading was recorded for each plot in each environment. Rate of senescence was calculated as the slope of the linear NDVI decline over accumulated growing degree days (AGDD) based

on Harris _et al_.46 and Lopes & Reynolds47. Stay green score was estimated using the predicted NDVI value at physiological maturity according to Lopes & Reynolds47. Specifically,

the linear regression equation obtained from the NDVI decay during grain-filling against accumulated AGDD after heading was first generated, and then days to physiological maturity was

introduced into the equation to calculate the corresponding NDVI value. $${\rm{ND}}\widehat{{{\rm{VI}}}_{{\rm{AGDD}}}}=m{\rm{AGDD}}+b$$

$${{\rm{NDVI}}}_{{\rm{PM}}}=m{{\rm{AGDD}}}_{{\rm{PM}}}+b$$ where NDVIAGDD is the simulated NDVI value at AGDD (°C days), NDVIPM (i.e. SG value) is the predicted NDVI value of AGDD at

physiological maturity, AGDDPM is the AGDD at physiological maturity, _m_ and _b_ is the slope and intercept of the linear regression model, respectively. Grain yield was calculated by

dividing total grain weight from each plot by the plot area, adjusted to 12% moisture level and expressed in kg ha-1. Heading date was recorded as the number of days from planting date to

the day when 50% spikes emerged in each plot. GENOTYPIC DATA ANALYSIS High quality DNA was isolated from freeze-dried, powdered leaf tissue (~100 mg) collected from two-week-old plants using

a modified cetyltrimethylammonium bromide protocol48,49. The genotyping-by-sequencing (GBS) libraries were prepared using _MspI_ and _PstI-_HF restriction enzymes50. The libraries were

pooled together in 96-plex and sequenced in an Ion Torrent Proton sequencer (Thermo Fisher Scientific, Waltham, MA, USA) following manufacturer’s instructions at the USDA Central Small Grain

Genotyping Lab, Kansas State University, Manhattan, KS, USA. All 242 soft wheat lines were genetically characterized using GBS approach51. SNP calling was performed using the TASSEL v5.0

GBS v2.0 discovery pipeline52. From the initial set of 448,307 sites, 49,406 SNPs remained after filtering markers with more than 80% of missing data and minor allele frequency less than

0.05. Missing values were imputed with LD-KNNi method53 implemented in TASSEL v.5. A Fisher exact test was used to test if the SNP alleles were independent in a population of inbred lines as

described by Poland _et al_.54. The SNPs were assumed allelic in the population if the null hypothesis of independence for the two alleles was rejected (_P_ < 0.001). This procedure

typically lowers heterozygous calls due to sequencing errors, genome duplications, and homologous sequences on different genomes50,54,55. In the final genomic dataset, a total of 19,353 SNPs

remained. PHENOTYPIC DATA ANALYSIS Least squares mean (LSmean) and standard error of grain yield and physiological traits for each environment were obtained using the following model with

genotype as a fixed effect and location and block as random effects: $${Y}{{\prime} }_{{ijk}}=\mu +G{g}_{j}+{E}_{i}+{B}_{i(k)}+Gg{E}_{ji}+{e}_{ijk}$$ (1) where _Y__ijk_ is the observed

value; µ was the general genotype mean; \(G{g}_{j}\) is the genotypic effect (j = 1 to 242); \({E}_{i}\) is the environment effect (i = 1 to 4, corresponding to Citra 2016, Citra 2017, Citra

2018, and Quincy 2017); \({B}_{j(k)}\) is the block effect (k = 1 to 12) within the ith environment; \(Gg{E}_{ji}\) is the jth genotype by ith environment interaction effect; and

\({e}_{ijk}\) is the random error. To evaluate the influence of phenology, DTH was included as a covariate in model (1) when calculating LSmeans (i.e. corrected GY). Therefore, two sets of

data including LSmeans of corrected and uncorrected GY were used for all following analyses, separately. To calculate broad sense heritability (_H_2) of grain yield and physiological traits

for each environment, the following model was used to obtain variance of each effect: $${Y}{{\prime} }_{{ij}}=\mu +G{g}_{j}+{B}_{k}+{e}_{jk}$$ (2) In this model, genotype and block were

considered as random effects. Broad sense heritability (_H_2) from each environment was calculated using the following formula, H2 = (σ2G)/(σ2G+σ2e), where, σ2G and σ2e were variances due to

genotype and error, respectively. LSmeans were for all traits at each location and used for Pearson correlation analyses between grain yield and other traits. Difference in LSmeans for all

the traits among environments was claimed to be significant at _P_ = 0.05 using Tukey’s Post-Hoc test. PREDICTION MODELS According to Montesinos-López _et al_.16, Krause _et al_.17 and

Jarquín _et al_.56, six BLUP of models incorporated with combinations of marker information (_G_), physiological data (_P_), marker × environment (_G_ × _E_), and physiological data ×

environment (_P_ × _E_) were proposed to assess the prediction accuracy of grain yield. Environmental effect was considered as a fixed effect in all models. Accordingly, the following

models, models (3) to (8), were fitted as _G_ only, _G_ + _G_ × _E_, _G_ + _P_ × _E_, _P_ only, _P_ + _P_ × _E_, and _P_ + _G_ × _E_, respectively: $${\rm{G}}:{Y}_{ij}=\mu

+{E}_{i}+{G}_{j}+{\varepsilon }_{ij}$$ (3) $${\rm{G}}+{{\rm{G}}}^{\ast }{\rm{Env}}:{Y}_{ij}=\mu +{E}_{i}+{G}_{j}+G{E}_{ij}+{\varepsilon }_{ij}$$ (4) $${\rm{G}}+{{\rm{P}}}^{\ast

}{\rm{Env}}:{Y}_{ij}=\mu +{E}_{i}+{G}_{j}+P{E}_{li}+{\varepsilon }_{ij}$$ (5) $${\rm{P}}:{Y}_{ij}=\mu +{E}_{i}+{P}_{l}+{\varepsilon }_{il}$$ (6) $${\rm{P}}+{{\rm{P}}}^{\ast

}{\rm{Env}}:{Y}_{ij}=\mu +{E}_{i}+{P}_{l}+\ast P{E}_{li}+{\varepsilon }_{il}$$ (7) $${\rm{P}}+{{\rm{G}}}^{\ast }{\rm{Env}}:{Y}_{ij}=\mu +{E}_{i}+{P}_{l}+G{E}_{ji}+{\varepsilon }_{il}$$ (8)

Where _Y__ij_ is the LSmean of GY for _j_th genotype in _i_th environment; _μ_ is the overall mean; \({E}_{i}\) is the environment effect (_i_ = 1 to 4, corresponding to Citra 2016, Citra

2017, Citra 2018, and Quincy 2017); \({G}_{j}\) is the genetic main effect (_j_ = 1 to 242); the genetic main effect is assumed as a joint distribution of genotype effect with a multivariate

normal distribution \(G={({G}_{1},\ldots ,{G}_{j\ast })}^{T}\sim MN(0,\,{\sigma }_{G}^{2}{\boldsymbol{G}})\), where \({\sigma }_{G}^{2}\) denotes the genomic variance and _G_ represents the

genomic relationship matrix; the _G_ matrices were calculated as \({\boldsymbol{G}}=\frac{{\boldsymbol{X}}{\boldsymbol{X}}{\boldsymbol{{\prime} }}}{n}\), where _X_ is a matrix of the

centered and standardized SNP marker matrix and _n_ is the number of SNP markers; \(G{E}_{ji}\) is the _j__t_h genotype by _i_th environment interaction effect; The term \(G{E}_{ji}\) was

assumed to have a multivariate normal distribution, that is \(G{E}_{ji}={(G{E}_{11},\ldots ,G{E}_{ji})}^{T} \sim MN(0,\,({Z}_{g}G{Z}_{g}^{T})\#({Z}_{E}{G}_{E}^{T}({\sigma }_{GE}^{2})\) where

\({Z}_{g}\) and \({Z}_{E}\) are incidence matrices for the vector of genomics and environment effects, and \({\sigma }_{GE}^{2}\) is the variance component for \(G{E}_{ji}\); \({P}_{l}\) is

the physiological main effect for genotype _l_ with the joint distribution of six physiological traits as \(P={({P}_{1},\ldots ,{P}_{l\ast })}^{T}\sim MN(0,\,{\sigma

}_{P}^{2}{\boldsymbol{P}})\); where \({\sigma }_{P}^{2}\) denotes the physiological trait variance and _P_ represents the physiological trait-derived relationship matrix, the _P_ matrices

were calculated as \({\boldsymbol{P}}=\frac{{\boldsymbol{S}}{\boldsymbol{S}}{\boldsymbol{{\prime} }}}{m}\), where _S_ is a matrix of the centered and standardized LSmeans of six

physiological traits and _m_ is the number of physiological variables; \(P{E}_{li}\) is the physiological matrices of _l__t_h genotype by _i_th environment interaction effect; and

\({\varepsilon }_{il}\) was the random error. The term \(P{E}_{li}\) was assumed to have a multivariate normal distribution, that is \(P{E}_{li}={(P{E}_{11},\ldots ,P{E}_{li})}^{T}\sim

MN(0,\,({Z}_{g}P{Z}_{g}^{T})\#({Z}_{E}{Z}_{E}^{T}){\sigma }_{PE}^{2})\) where \({Z}_{g}\) and \({Z}_{E}\) are incidence matrices for the vector of genomics and environment effects, and

\({\sigma }_{PE}^{2}\) is the variance component for \(P{E}_{li}\) (Krause _et al_.; Jarquín _et al_. 2014). MODEL PREDICTION ACCURACY For each environment, all six models were evaluated

using a five-fold cross validation approach for their prediction accuracies. Briefly, the association panel was partitioned into five equally sized (or similar) subgroups. Four of the five

subgroups (i.e., the TP) were used to fit each prediction model while the remaining subgroup (i.e., the VP) was used to assess the correlation between the observed and predicted trait

values. This process was repeated five times, with each subgroup being used as the prediction set for once. To control the relatedness among lines, the population was stratified based on

discriminant analysis of principal components (_DAPC_)57 clustering analysis, so that lines belonging to the same group were present in either validation or training population, not in both

simultaneously. Prediction accuracies were calculated as \({r}_{GY}={r}_{{\rm{p}}}/\sqrt{{H}^{2}}\), where \({r}_{{\rm{p}}}\) is the mean predictive correlations across five folds. Standard

error of prediction accuracy for each environment and each model was calculated based on \({{\rm{SE}}}_{GYP}={{\rm{\sigma }}}_{{r}_{p}}/\sqrt{f{H}^{2}}\), where \({{\rm{\sigma

}}}_{{r}_{p}}\) is the standard deviation of the predictive correlation;\(\,f\) is the number of folds (5 in this case). The same procedure was performed for GY corrected for phenology (i.e.

DTH included as a covariate). In order to further evaluate the performance of prediction models, response to selection (RTS) was calculated using the formula _R_ = _H__2__S_31, where _H_2

is the heritability for grain yield; and _S_ is the selection differential (in unit of kg ha−1). In specific, all 242 lines were ordered according to their GEBV calculated from each model in

each environment. The top 10% lines were then chosen as the selected population (i.e. selection intensity of 10%). Selection differential was calculated as the difference of grain yield

between the means of selected lines and whole population: _S_ = μS – μP, where μS is the mean yield of 10% selected lines based on GEBV and μP is the mean yield of population. Response to

selection for all six models at each environment were computed with and without correction for DTH. Mean of RTS was calculated for each environment and each model across five folds. Standard

error of RTS was calculated based on \({{\rm{SE}}}_{GYRTS}={{\rm{\sigma }}}_{RTS}/\sqrt{f}\), where \({{\rm{\sigma }}}_{RTS}\) is the standard deviation of the RTS; \(f\) is the number of

folds (5 in this case). MULTI-VARIATE ANALYSIS FOR PHYSIOLOGICAL TRAITS In order to dissect the inter-relationships between GY and physiological traits, a machine learning based clustering

analysis was performed using CARET (Classification and Regression Training) technique in R. A multi-variate prediction model on GY were created using all physiological traits collected from

the field. In specific, the physiological data was firstly standardized and centered before subjecting into regularized regression models that employ strict penalties to prevent overfitting.

The penalty parameters control the levels of shrinkage of the coefficients for correlated predictors. In CARET, regularization path is computed for the LASSO or elastic net penalty at a

grid of values for the regularization parameter alpha and lambda. A bootstrap training procedure with a 10-fold cross-validation and 20 repetitions was used to evaluate the performance of

different penalty levels on GY prediction. A final model was selected based on the smallest mean squared error obtained in the training procedure. The magnitude of importance of

physiological trait contributing to GY was compared based on the absolute value of scaled coefficients, with/without DTH corrected as a covariate. The dataset from Citra 2017 was used for

the analysis since all 11 physiological traits were collected. SOFTWARE Phenotypic data analysis, including LSmeans and heritability calculation, and correlation analyses, were performed

using R (R Development Core Team 2018). Basic models (1-2) were fit with the “lme4” package58. Prediction models (3-8) were fit with package “BGLR”59. The _DAPC_ analysis was performed using

“adegenet” package60. Cross-validation and prediction accuracy calculation were conducted using customized codes in R. Clustering analysis for physiological traits was performed using

“caret” package61. DATA AVAILABILITY All data generated or analyzed during this study are available from the corresponding author on reasonable request. REFERENCES * Meuwissen, T., Hayes, B.

& Goddard, M. Prediction of total genetic value using genome-wide dense marker maps. _Genetics_ 157, 1819–1829 (2001). PubMed  PubMed Central  CAS  Google Scholar  * Battenfield, S. D.

_et al_. Genomic selection for processing and end-use quality traits in the CIMMYT spring bread wheat breeding program. _The Plant Genome_ 9 (2016). * Eathington, S. R., Crosbie, T. M.,

Edwards, M. D., Reiter, R. S. & Bull, J. K. Molecular markers in a commercial breeding program. _Crop. Sci._ 47, S-154–S-163 (2007). Article  Google Scholar  * Cabrera-Bosquet, L.,

Crossa, J., von Zitzewitz, J., Serret, M. D. & Luis Araus, J. High‐throughput Phenotyping and Genomic Selection: The Frontiers of Crop Breeding Converge F. _J. Integr. plant. Biol._ 54,

312–3C0 (2012). Article  PubMed  Google Scholar  * Araus, J. L. & Cairns, J. E. Field high-throughput phenotyping: the new crop breeding frontier. _Trends Plant. Sci._ 19, 52–61 (2014).

Article  PubMed  CAS  Google Scholar  * Jannink, J.-L., Lorenz, A. J. & Iwata, H. Genomic selection in plant breeding: from theory to practice. _Brief. Funct. genomics_ 9, 166–177

(2010). Article  PubMed  CAS  Google Scholar  * Lorenz, A. J. _et al_. In _Advances in agronomy_ Vol. 110 77–123 (Elsevier, 2011). * Buckler, E. S. _et al_. The genetic architecture of maize

flowering time. _Science_ 325, 714–718 (2009). Article  ADS  PubMed  CAS  Google Scholar  * Burgueño, J., Crossa, J., Cotes, J. M., Vicente, F. S. & Das, B. Prediction assessment of

linear mixed models for multienvironment trials. _Crop. Sci._ 51, 944–954 (2011). Article  Google Scholar  * So, Y.-S. & Edwards, J. Predictive ability assessment of linear mixed models

in multienvironment trials in corn. _Crop. Sci._ 51, 542–552 (2011). Article  Google Scholar  * Montesinos-López, O. A. _et al_. Predicting grain yield using canopy hyperspectral reflectance

in wheat breeding data. _Plant. methods_ 13, 4 (2017). Article  PubMed  PubMed Central  Google Scholar  * Aguate, F. M. _et al_. Use of hyperspectral image data outperforms vegetation

indices in prediction of maize yield. _Crop. Sci._ 57, 2517–2524 (2017). Article  CAS  Google Scholar  * Pérez-Rodríguez, P. _et al_. Single-step genomic and pedigree genotype× environment

interaction models for predicting wheat lines in international environments. _The plant genome_ (2017). * Cuevas, J. _et al_. Bayesian genomic prediction with genotype× environment

interaction kernel models. _G3: Genes, Genomes, Genet._ 7, 41–53 (2017). Article  CAS  Google Scholar  * Crain, J., Mondal, S., Rutkoski, J., Singh, R. P. & Poland, J. Combining

high-throughput phenotyping and genomic information to increase prediction and selection accuracy in wheat breeding. _The plant genome_ (2018). * Montesinos-López, A. _et al_. Genomic

Bayesian functional regression models with interactions for predicting wheat grain yield using hyper-spectral image data. _Plant. Methods_ 13, 62 (2017). Article  PubMed  PubMed Central  CAS

  Google Scholar  * Krause, M. R. _et al_. Hyperspectral Reflectance-Derived Relationship Matrices for Genomic Prediction of Grain Yield in Wheat. _G3: Genes, Genomes, Genet._ G3,

200856.202018 (2019). Google Scholar  * Blum, A., Shpiler, L., Golan, G. & Mayer, J. Yield stability and canopy temperature of wheat genotypes under drought-stress. _Field Crop. Res_ 22,

289–296 (1989). Article  Google Scholar  * Amani, I., Fischer, R. & Reynolds, M. Canopy temperature depression association with yield of irrigated spring wheat cultivars in a hot

climate. _J. Agron. Crop. Sci._ 176, 119–129 (1996). Article  Google Scholar  * Bavec, F. & Bavec, M. Chlorophyll meter readings of winter wheat cultivars and grain yield prediction.

_Commun. Soil. Sci. Plant. Anal._ 32, 2709–2719 (2001). Article  MATH  CAS  Google Scholar  * Blum, A., Klueva, N. & Nguyen, H. Wheat cellular thermotolerance is related to yield under

heat stress. _Euphytica_ 117, 117–123 (2001). Article  Google Scholar  * Raun, W. R. _et al_. In-season prediction of potential grain yield in winter wheat using canopy reflectance. _Agron.

J._ 93, 131–138 (2001). Article  Google Scholar  * Monostori, I. _et al_. Relationship between SPAD value and grain yield can be affected by cultivar, environment and soil nitrogen content

in wheat. _Euphytica_ 211, 103–112 (2016). Article  CAS  Google Scholar  * Weber, V. _et al_. Prediction of grain yield using reflectance spectra of canopy and leaves in maize plants grown

under different water regimes. _Field Crop. Res._ 128, 82–90 (2012). Article  Google Scholar  * De los Campos, G., Gianola, D., Rosa, G. J., Weigel, K. A. & Crossa, J. Semi-parametric

genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. _Genet. Res._ 92, 295–308, https://doi.org/10.1017/S0016672310000285 (2010). Article  CAS 

Google Scholar  * Gianola, D. & van Kaam, J. B. Reproducing kernel hilbert spaces regression methods for genomic assisted prediction of quantitative traits. _Genetics_ 178, 2289–2303,

https://doi.org/10.1534/genetics.107.084285 (2008). Article  PubMed  PubMed Central  Google Scholar  * Pérez, P., de los Campos, G., Crossa, J. & Gianola, D. Genomic-enabled prediction

based on molecular markers and pedigree using the Bayesian linear regression package in R. _plant. genome_ 3, 106–116 (2010). Article  PubMed  PubMed Central  Google Scholar  * Pérez, P.

& de Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. _Genetics_ 198, 483–495 (2014). Article  PubMed  PubMed Central  Google Scholar  * Xu, Y.,

Xu, C. & Xu, S. Prediction and association mapping of agronomic traits in maize using multiple omic data. _Heredity_ 119, 174 (2017). Article  PubMed  PubMed Central  CAS  Google Scholar

  * Rutkoski, J. _et al_. Canopy temperature and vegetation indices from high-throughput phenotyping improve accuracy of pedigree and genomic selection for grain yield in wheat. _G3: Genes,

Genomes, Genet._ 6, 2799–2808 (2016). Article  Google Scholar  * Falconer, D. S. & Mackay, T. F. C. Introduction to quantitative genetics. 4th edn, (Longman, 1996). * Aparicio, N.,

Villegas, D., Casadesus, J., Araus, J. L. & Royo, C. Spectral vegetation indices as nondestructive tools for determining durum wheat yield. _Agron. J._ 92, 83–91 (2000). Article  Google

Scholar  * Royo, C. _et al_. Usefulness of spectral reflectance indices as durum wheat yield predictors under contrasting Mediterranean conditions. _Int. J. Remote. Sens._ 24, 4403–4419

(2003). Article  ADS  Google Scholar  * Marti, J., Bort, J., Slafer, G. & Araus, J. Can wheat yield be assessed by early measurements of Normalized Difference Vegetation Index? _Ann.

Appl. Biol._ 150, 253–257 (2007). Article  Google Scholar  * Babar, M. _et al_. Spectral reflectance indices as a potential indirect selection criteria for wheat yield under irrigation.

_Crop. Sci._ 46, 578–588 (2006). Article  Google Scholar  * Tattaris, M., Reynolds, M. P. & Chapman, S. C. A direct comparison of remote sensing approaches for high-throughput

phenotyping in plant breeding. _Front. Plant. Sci._ 7, 1131 (2016). Article  PubMed  PubMed Central  Google Scholar  * Khan, Z., Rahimi-Eichi, V., Haefele, S., Garnett, T. & Miklavcic,

S. J. Estimation of vegetation indices for high-throughput phenotyping of wheat using aerial imaging. _Plant. methods_ 14, 20 (2018). Article  PubMed  PubMed Central  Google Scholar  *

Rischbeck, P. _et al_. Data fusion of spectral, thermal and canopy height parameters for improved yield prediction of drought stressed spring barley. _Eur. J. Agron._ 78, 44–59 (2016).

Article  Google Scholar  * Fischer, R. _et al_. Wheat yield progress associated with higher stomatal conductance and photosynthetic rate, and cooler canopies. _Crop. Sci._ 38, 1467–1475

(1998). Article  Google Scholar  * Araus, J., Slafer, G., Reynolds, M. & Royo, C. Plant breeding and drought in C3 cereals: what should we breed for? _Ann. Bot_ 89, 925–940 (2002).

Article  PubMed  PubMed Central  Google Scholar  * Pinto, R. S. _et al_. Heat and drought adaptive QTL in a wheat population designed to minimize confounding agronomic effects. _Theor. Appl.

Genet._ 121, 1001–1021 (2010). Article  PubMed  PubMed Central  Google Scholar  * Reynolds, M., Balota, M., Delgado, M., Amani, I. & Fischer, R. Physiological and morphological traits

associated with spring wheat yield under hot, irrigated conditions. _Funct. Plant. Biol._ 21, 717–730 (1994). Article  Google Scholar  * Gutiérrez-Rodríguez, M., Reynolds, M. P.,

Escalante-Estrada, J. A. & Rodríguez-González, M. T. Association between canopy reflectance indices and yield and physiological traits in bread wheat under drought and well-irrigated

conditions. _Aust. J. Agric. Res_ 55, 1139–1147 (2004). Article  Google Scholar  * Rosyara, U. R., Subedi, S., Duveiller, E. & Sharma, R. C. Photochemical efficiency and SPAD value as

indirect selection criteria for combined selection of spot blotch and terminal heat stress in wheat. _J. Phytopathol_ 158, 813–821 (2010). Article  Google Scholar  * Ibrahim, A. M. &

Quick, J. S. Genetic control of high temperature tolerance in wheat as measured by membrane thermal stability. _Crop. Sci._ 41, 1405–1407 (2001). Article  Google Scholar  * Harris, K. _et

al_. Sorghum stay-green QTL individually reduce post-flowering drought-induced leaf senescence. _J. Exp. Botany_ 58, 327–338, https://doi.org/10.1093/jxb/erl225 (2006). Article  CAS  Google

Scholar  * Lopes, M. S. & Reynolds, M. P. Stay-green in spring wheat can be determined by spectral reflectance measurements (normalized difference vegetation index) independently from

phenology. _J. Exp. Botany_ 63, 3789–3798, https://doi.org/10.1093/jxb/ers071 (2012). Article  CAS  Google Scholar  * Doyle, J. A rapid DNA isolation procedure for small quantities of fresh

leaf tissue. _Phytochem. Bull_ 19, 11–15 (1987). Google Scholar  * Doyle, J. J. & Doyle, J. L. A rapid DNA isolation procedure for small quantities of fresh leaf tissue. (1987). *

Poland, J. A., Brown, P. J., Sorrells, M. E. & Jannink, J.-L. Development of high-density genetic maps for barley and wheat using a novel two-enzyme genotyping-by-sequencing approach.

_PLoS one_ 7, e32253, https://doi.org/10.1371/journal.pone.0032253 (2012). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Elshire, R. J. _et al_. A robust, simple

genotyping-by-sequencing (GBS) approach for high diversity species. _PLoS one_ 6, e19379 (2011). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Bradbury, P. J. _et al_. TASSEL:

software for association mapping of complex traits in diverse samples. _Bioinformatics_ 23, 2633–2635, https://doi.org/10.1093/bioinformatics/btm308 (2007). Article  PubMed  CAS  Google

Scholar  * Money, D. _et al_. LinkImpute: Fast and Accurate Genotype Imputation for Nonmodel Organisms. _G3: Genes|Genomes|Genetics_ 5, 2383–2390, https://doi.org/10.1534/g3.115.021667

(2015). Article  PubMed  PubMed Central  Google Scholar  * Poland, J. _et al_. Genomic Selection in Wheat Breeding using Genotyping-by-Sequencing. _The Plant_. _Genome_ 5, 103–113,

https://doi.org/10.3835/plantgenome2012.06.0006 (2012). Article  CAS  Google Scholar  * Bansal, V. _et al_. Accurate detection and genotyping of SNPs utilizing population sequencing data.

_Genome Res_ 20, 537–545, https://doi.org/10.1101/gr.100040.109 (2010). Article  PubMed  PubMed Central  CAS  Google Scholar  * Jarquín, D. _et al_. A reaction norm model for genomic

selection using high-dimensional genomic and environmental data. _Theor. Appl. Genet._ 127, 595–607 (2014). Article  PubMed  Google Scholar  * Jombart, T., Devillard, S. & Balloux, F.

Discriminant analysis of principal components: a new method for the analysis of genetically structured populations. _BMC Genet._ 11, 94, https://doi.org/10.1186/1471-2156-11-94 (2010).

Article  PubMed  PubMed Central  Google Scholar  * Bates, D., Sarkar, D., Bates, M. D. & Matrix, L. The lme4 package. _R package version_ 2, 74 (2007). * de los Campos, G. &

Pérez-Rodríguez, P. Bayesian generalized linear regression. _R package version_ 1 (2014). * Jombart, T. adegenet: a R package for the multivariate analysis of genetic markers.

_Bioinformatics_ 24, 1403–1405 (2008). Article  PubMed  CAS  Google Scholar  * Kuhn, M. Building Predictive Models in R Using the caret Package. _2008_ 28, 26,

https://doi.org/10.18637/jss.v028.i05 (2008). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This research was funded by UF/IFAS early career award. AUTHOR INFORMATION Author

notes * These authors contributed equally: Jia Guo and Sumit Pradhan. AUTHORS AND AFFILIATIONS * Department of Agronomy, University of Florida, Gainesville, FL, USA Jia Guo, Sumit Pradhan, 

Dipendra Shahi, Jahangir Khan, Jordan Mcbreen & Md Ali Babar * USDA-ARS Central Small Grain Genotyping Lab, Manhattan, Kansas, USA Guihua Bai * Crop and Soil Sciences, North Carolina

State University, Raleigh, North Carolina, USA J. Paul Murphy Authors * Jia Guo View author publications You can also search for this author inPubMed Google Scholar * Sumit Pradhan View

author publications You can also search for this author inPubMed Google Scholar * Dipendra Shahi View author publications You can also search for this author inPubMed Google Scholar *

Jahangir Khan View author publications You can also search for this author inPubMed Google Scholar * Jordan Mcbreen View author publications You can also search for this author inPubMed 

Google Scholar * Guihua Bai View author publications You can also search for this author inPubMed Google Scholar * J. Paul Murphy View author publications You can also search for this author

inPubMed Google Scholar * Md Ali Babar View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.A.B. designed the project. S.P. carried out

experiment and data collection. J.G. data analysis and writing manuscript. G.B. provided genomic data. M.A.B. and G.B. and J.P.M edited manuscript. D.S. and J.K. and J.M. collected data in

the field. CORRESPONDING AUTHOR Correspondence to Md Ali Babar. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Guo, J., Pradhan,

S., Shahi, D. _et al._ Increased Prediction Accuracy Using Combined Genomic Information and Physiological Traits in A Soft Wheat Panel Evaluated in Multi-Environments. _Sci Rep_ 10, 7023

(2020). https://doi.org/10.1038/s41598-020-63919-3 Download citation * Received: 17 July 2019 * Accepted: 11 March 2020 * Published: 27 April 2020 * DOI:

https://doi.org/10.1038/s41598-020-63919-3 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative