Equilibrium Thermodynamic Properties of Aqueous Solutions of Ionic Liquid 1-Ethyl-3-Methylimidazolium Methanesulfonate [EMIM][MeSO3]

Download PDF Article Open access Published: 21 February 2020 Equilibrium Thermodynamic Properties of Aqueous Solutions of Ionic Liquid 1-Ethyl-3-Methylimidazolium Methanesulfonate

[EMIM][MeSO3] Chaolun Zheng1, Jian Zhou1, Yong Pei1 & …Bao Yang  ORCID: orcid.org/0000-0003-1971-21741 Show authors Scientific Reports volume 10, Article number: 3174 (2020) Cite this

article

3198 Accesses

7 Citations

1 Altmetric

Metrics details

The ionic liquid 1-ethyl-3-methylimidazolium methanesulfonate ([EMIM][MeSO3]) has been considered as a promising alternative desiccant to triethylene glycol and lithium bromide commonly used

in the industry. In this paper, the water activity coefficient of this binary system was measured from 303 K to 363 K with water concentration from 18% to 92%. The interaction energies

between the ionic liquid molecules (\({g}_{22}\)) and between the ionic liquid and water molecules (\({g}_{12}\)) for the [EMIM][MeSO3]/water binary system were determined from the water

activity coefficient data using the Non-Random Two-Liquid (NRTL) model. The magnitude of the interaction energy between the [EMIM][MeSO3] and water molecules (\({g}_{12}\)) was found to be

in the range of 45~49 kJ/mol, which was about 20% larger than that between the water molecules (\({g}_{11}\)) in the [EMIM][MeSO3]/water system. The large (\({g}_{12}\)) can explain many

observed macroscopic thermodynamic properties such as strong hygroscopicity in the ionic liquid [EMIM][MeSO3]. These interaction energies were used to determine the heat of desorption of the

[EMIM][MeSO3]/water system, and the obtained heat of desorption was in good agreement with that calculated from the conventional Clausius-Clapeyron Equation.

viewed by others Investigating the phase diagram-ionic conductivity isotherm relationship in aqueous solutions of common acids: hydrochloric, nitric, sulfuric and phosphoric acid Article

Open access 03 April 2024 A new method based on binary mixture concept for prediction of ionic liquids critical properties using molecular dynamics simulation Article Open access 04 March

2025 Thermodynamic studies of solute–solute and solute–solvent interactions in ternary aqueous systems containing {betaine + PEGDME250} and {betaine + K3PO4 or K2HPO4} at 298.15 K Article

Open access 18 October 2023 Introduction

Ionic liquids are compounds composed of organic cations and inorganic anions, and they show a negligible vapor pressure and good fluidity over a wide temperature range1,2. Some ionic liquids

have been found to be highly hygroscopic, which makes them promising desiccants for applications in gas dehydration and absorption cooling. In contrast to triethylene glycol currently used

in gas dehydration, losses by evaporation can be eliminated when the ionic liquids are used as desiccants. In addition, the use of ionic liquids can avoid the crystallization and corrosion

problems3,4, which are the two major concerns of the most commonly used halide salt liquid desiccants5,6.

The ionic liquid 1-ethyl-3-methylimidazolium methanesulfonate ([EMIM][MeSO3]) is among those that are highly hygroscopic, and is a promising candidate for next generation of desiccants7,8.

The determination of thermodynamic properties is important for performance evaluation for this special ionic liquid. Many researchers have conducted experiments to measure the important

macroscopic thermodynamic properties, such as specific heat9,10, density7,9,10,11,12, viscosity7,9,11,13, electrical conductivity9, surface tension11,14, reflective index11, diffusion

coefficient7, nuclear magnetic resonance (NMR) spectroscopy9,14,15, excess molar heats of mixing9,12,16, and water activity coefficient7,16.

Although the macroscopic thermodynamic properties of the [EMIM][MeSO3]/water binary system have been extensively investigated, the molecular thermodynamic properties of this binary system

are not comprehensive. For example, the interaction energy or bonding energy between the ionic liquid molecules, and between the ionic liquid and water molecules are extremely scarce for the

ionic liquid [EMIM][MeSO3]/water systems. These molecular interaction energy properties are related to many macroscopic thermodynamic properties such as heat of desorption, heat capacity,

hygroscopicity, and water vapor pressure.

In this work, the Non-Random Two-Liquid (NRTL) model was used to determine the interaction energies between different molecule pairs inside the [EMIM][MeSO3]/water binary system from the

measured water activity coefficients data. These interaction energies were used to determine the heat of desorption of the [EMIM][MeSO3]/water system, which was in good agreement with those

calculated from the Clausius-Clapeyron Equation. A formula to predict heat of desorption from the interaction energies was also developed for the binary systems.

BackgroundWater activity coefficient

The activity coefficient of water \({\gamma }_{{{\rm{H}}}_{2}{\rm{o}}}\) is a fundamental thermodynamic parameter that accounts for deviations from ideal behavior in non-ideal solutions,

such as the aqueous ionic liquid solutions, which is defined as7,8:

{\rm{ideal}}}}{{p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{ideal}}}}=\frac{{p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{non}} \mbox{-} {\rm{ideal}}}}{{x}_{{{\rm{H}}}_{2}{\rm{O}}}\cdot

{p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{sat}}}}$$ (1)

where \({p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{ideal}}}\) and \({p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{non}} \mbox{-} {\rm{ideal}}}\) are the partial pressure of water above the ideal and non-ideal

aqueous solutions, respectively, \(\,{p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{sat}}}\) is the saturation pressure of pure water, and \({x}_{{{\rm{H}}}_{2}{\rm{O}}}\) is the molar fraction of water

in the aqueous solutions. In Eq. (1), the ratio \({p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{non}} \mbox{-} {\rm{ideal}}}/{p}_{{{\rm{H}}}_{2}{\rm{O}},{\rm{sat}}}\) is the relative humidity (RH) of the

non-ideal aqueous solutions. In the ideal aqueous solutions, the partial pressure of water can be described by Raoult’s

law7:

However, the [EMIM][MeSO3]/water solution is a non-ideal solution, in which the interaction energy between [EMIM][MeSO3] and water is significantly stronger than those between water and

water. A small value of water activity coefficient \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) indicates a large intermolecular force between water and ionic liquid molecules and strong

hygroscopicity for water absorption. The water activity coefficient at infinite dilution \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) is often used for the comparison of the hygroscopicity

or absorption strength of different desiccants7.

The NRTL model17,18,19,20 correlates the activity coefficients \({\gamma }_{i}\) of a compound i with its mole fractions \({x}_{i}\) in the liquid solutions:

}_{1}={x}_{2}^{2}(\frac{\Delta {g}_{12-11}}{RT}\frac{\exp (\,-\,2{\alpha }_{12}\Delta {g}_{12-11}/RT)}{{[{x}_{1}+{x}_{2}\exp (-{\alpha }_{12}\Delta {g}_{12-11}/RT)]}^{2}}+\frac{\Delta

{g}_{12-22}}{RT}\frac{\exp (\,-\,{\alpha }_{12}\Delta {g}_{12-22}/RT)}{{[{x}_{2}+{x}_{1}\exp (-{\alpha }_{12}\Delta {g}_{12-22}/RT)]}^{2}})$$ (3) $$\mathrm{ln}\,{\gamma

}_{2}={x}_{1}^{2}(\frac{\Delta {g}_{12-22}}{RT}\frac{\exp (\,-\,2{\alpha }_{12}\Delta {g}_{12-22}/RT)}{{[{x}_{2}+{x}_{1}\exp (-{\alpha }_{12}\Delta {g}_{12-22}/RT)]}^{2}}+\frac{\Delta

{g}_{12-11}}{RT}\frac{\exp (\,-\,{\alpha }_{12}\Delta {g}_{12-11}/RT)}{{[{x}_{1}+{x}_{2}\exp (-{\alpha }_{12}\Delta {g}_{12-11}/RT)]}^{2}})$$ (4)

where the subscripts 1 and 2 refer to component 1 and component 2 in the binary solution, respectively, \(\Delta {g}_{12-11}\) and \(\Delta {g}_{12-22}\,\)are the exchange in the interaction

energy between molecules, \({\alpha }_{12}\) is the non-randomness parameter, R is the molar gas constant, and T is the absolute temperature. In the case of infinite dilution, the NRTL

equations reduce to

$$\mathrm{ln}\,{\gamma }_{2,\infty }=\frac{\Delta {g}_{12-22}}{RT}+\frac{\Delta {g}_{12-11}}{RT}\exp (\,-\,{\alpha }_{12}\Delta {g}_{12-11}/RT)$$ (6)

The water activity coefficient at infinite dilution \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) can be used to compare the hygroscopicity or absorption strength of different desiccants.

In the NRTL model, the exchange in the interaction energy \(\Delta {g}_{12-11}={g}_{12}-{g}_{11}\), which is the interaction energy change as a result of breaking a 1-1 interaction

\({g}_{11}\) and forming a 1–2 interaction \({g}_{12}\). In this study, components 1 and 2 refer to the water and the [EMIM][MeSO3], respectively. So \({g}_{11}\), \(\,{g}_{22}\), and

\({g}_{12}\) are the interaction energies between the water molecules, between the ionic liquid [EMIM][MeSO3] molecules, and between the water and [EMIM][MeSO3] molecules. The interaction

energy parameters \(\Delta {g}_{12-11}\) and \(\Delta {g}_{12-22}\) can be determined by data fitting using Eqs. (3) and (4) if the water activity coefficients \({\gamma

}_{{{\rm{H}}}_{2}{\rm{O}}}\) with its mole fraction \({x}_{{{\rm{H}}}_{2}{\rm{O}}}\) can be measured in the [EMIM][MeSO3]/water binary system. The interaction energy between the ionic liquid

and water molecules \({g}_{12}\) can be determined using the formula: \({g}_{12}=\Delta {g}_{12-11}+{g}_{11}\) if the interaction energy between water molecules \({g}_{11}\) is known.

Similarly, the interaction energy between the ionic liquid molecules \({g}_{22}\) can be determined by \({g}_{22}=\Delta {g}_{12-22}+{g}_{12}\). These molecular interaction energy properties

are related to many macroscopic thermodynamic properties such as heat of desorption, heat capacity, hygroscopicity, and water vapor pressure. One application of these molecular interaction

energies is that they can be used to predict the heat of desorption of the aqueous ionic liquid solutions with water concentration from 0% to 100%. In comparison, the Clausius-Clapeyron

Equation determines the heat of desorption at the water concentration where the vapor pressure and temperature are known.

The Clausius-Clapeyron Equation relates the vapor-liquid equilibrium (VLE) data (p and T) to the thermodynamic property, enthalpy of vaporization (\(\Delta {H}_{v}\)), which is given

by21

where \(p\) is the vapor pressure at the temperature T, \(\Delta {H}_{v}\) is enthalpy of vaporization, R is the molar gas constant, and \({\rm{C}}\) is a constant. In Eq. (7), \(\Delta

{H}_{v}\) is assumed to be independent of T. However, the temperature dependence of \(\Delta {H}_{v}\) cannot be overlooked in the water and [EMIM][MeSO3] binary solutions due to the complex

interaction between water and [EMIM][MeSO3]21,22. In a moderate temperature range, \(\Delta {H}_{v}\) can be assumed to change linearly with T,

(8)

where \(a\) is the temperature coefficient. So the modified Clausius–Clapeyron Equation for the ionic liquid solutions can be written as

follows:

Therefore \(\Delta {H}_{v}\) can be determined from Eqs. (8) and (9) when the VLE data are measured.

The experimental uncertainty in this experiment is estimated using the root-sum-square method suggested by Moffat23:

}\limits_{{\rm{i}}=1}^{{\rm{N}}}{(\frac{\partial R}{\partial {x}_{i}}{\rm{\delta }}{x}_{{\rm{i}}})}^{2}\}}^{1/2}$$ (10)

In particular, whenever the equation describing the result is a pure “product form”, as shown in Eq. (11):

the relative uncertainty can be calculated by Eq. (12):

{X}_{M}}{{X}_{M}})}^{2}\}}^{1/2}$$ (12) Experimental MethodsMaterials

The 1-ethyl-3-methylimidazolium methanesulfonate ([EMIM][MeSO3]) was purchased from Sigma-Aldrich (purity higher than 95 wt. %). Deionized water was used in the experiment.

setup

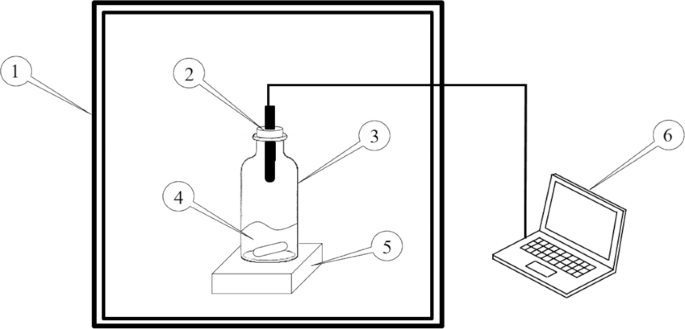
The experiment setup for the vapor-liquid equilibrium (VLE) measurement is shown in Fig. 1. The temperature during experiments was controlled using a temperature-controlled oven (Yamato,

DKN-402C). The [EMIM][MeSO3]/water solution was placed inside a reactant bottle, in which a humidity sensor (Rotronic HC2A-SM) was attached. The RH and temperature (T) of the gas phase

inside the reactant bottle were measured simultaneously using this humidity sensor with an uncertainty of T = ±0.1 K and RH = ±0.8% of the RH reading. The water concentration in

[EMIM][MeSO3]/water solutions was measured using the Karl Fisher Titrator (Mettler Toledo™ C20D) with a relative uncertainty less than 0.5%. A magnetic stirrer (Thermo Scientific Cimarec

Micro Stirrers) was used to stir the [EMIM][MeSO3]/water solution inside the reactant bottle during the VLE measurement. The data logging and the conversion from RH and T to water vapor

pressure were performed using the HW4-E software in a computer.

Schematic of the experimental setup for the VLE Measurements. Legend: 1. temperature-controlled oven; 2. humidity sensor; 3. reagent bottle; 4. [EMIM][MeSO3]/water solution; 5. magnetic

stirrer; 6. DAQ/computer.

Twelve [EMIM][MeSO3]/water solutions with molar concentration of water from 18% to 92% were prepared in the VLE measurements. For each solution, its RH was measured at temperatures 303 K,

323 K, 343 K, and 363 K. The sample solution with an approximate volume of 100 ml was placed in the reactant bottle. The oven temperature was set to the desired temperature, and the sample

solution was heated and stirred vigorously with magnetic stirrers to get homogeneous mixing. At the same time, the data logging was started. After the system reached the equilibrium and the

RH stayed unchanged for 30 minutes, the equilibrium temperature and RH were recorded. A series of equilibrium temperature and water vapor pressure (or RH) data were obtained for the

[EMIM][MeSO3]/water solutions.

The experimental VLE data for the [EMIM][MeSO3]/water binary solutions with water molar concentrations from 18% to 92% were measured and listed in Table 1. The vapor pressure

\({p}_{{{\rm{H}}}_{2}{\rm{O}}}\) were determined using the measured RH. The relative uncertainty of the measured mole fraction x(H2O) was found to be less than 5.02% using Eq. (12). The RH

and T were measured simultaneously using the humidity sensor with an uncertainty of T = ±0.1 K and RH = ±0.8% of the RH reading. Figure 2 shows the measured water vapor pressure in

[EMIM][MeSO3]/water binary solutions versus the molar fraction of water in a temperature range of 303 K to 363 K.

at different temperatures.Full size tableFigure 2

Water vapor pressure in the [EMIM][MeSO3]/water binary solutions versus the molar fraction of water in the temperature range of 303 K to 363 K.

The effect of the ionic liquid on the non-ideality of the aqueous solutions can be expressed by the activity coefficients of water \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\), which was

calculated by Eq. (1). Table 2 shows the calculated activity coefficients of water \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) in the [EMIM][MeSO3]/water binary solutions. The relative

uncertainty of the water activity coefficient \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) was found to be 5.09%. The plot of the activity coefficient \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) versus

the molar concentration of water is shown in Fig. 3. As shown in this figure, the water activity coefficient \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) approaches a value of one when the water

concentration is close to 100%, as expected by Raoult’s law. For water concentrations below about 30 mol.%, \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) approaches almost constant values between

0.10 and 0.15. A small value of \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\,\)indicates a large deviation from the ideal solution behavior or from Raoult’s law. A small value of \({\gamma

}_{{{\rm{H}}}_{2}{\rm{O}}}\,\)is desired for the application in gas dehydration. The influence of the temperature on \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) is small in the temperature range

of test, especially for low water concentrations. For a given water concentration, \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\) increases slightly when the temperature increases, which is

consistent with the temperature dependence of the interaction energy \(\Delta {g}_{12-11}\) in the [EMIM][MeSO3]/water binary solutions.

\({{\boldsymbol{\gamma }}}_{{{\rm{H}}}_{2}{\rm{O}}}\) of the [EMIM][MeSO3]/water binary solutions at different temperatures.Full size tableFigure 3

Activity coefficient of water in the [EMIM][MeSO3]/water binary solutions versus the molar fraction of water in the temperature range of 303 K to 363 K.

The water activity coefficients at infinite dilution \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) for the [EMIM][MeSO3]/water binary solutions are listed in Table 3. It is found that the

limiting water activity coefficients \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) is in the range of 0.102 to 0.151 at temperatures from 303 K to 363 K, more than 4 times lower than that

for triethylene glycol, which indicates that the ionic liquid [EMIM][MeSO3] possesses much stronger ability of absorbing water vapor than the commonly used triethylene glycol

desiccants.

temperatures.Full size table

There exist some discrepancies in \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) in literature. For example, Krannich et al.7 reported the \({{\rm{\gamma }}}_{{{\rm{H}}}_{2}{\rm{O}},\infty

}\) around 0.20 that was determined using the boiling point method. Domanska et al.16 reported the \({{\rm{\gamma }}}_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) in the range 0.071~0.088, which were

determined with the gas-liquid chromatography method. In this study, the limiting water activity coefficients \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) was found to be in the range of

0.102 to 0.151 at temperatures from 303 K to 363 K. The differences in the reported \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}},\infty }\) data might be due to the different measurement

techniques.

The exchange in interaction energy \(\Delta {g}_{12-11}\), and \(\Delta {g}_{12-22}\) and the non-randomness parameter \({\alpha }_{12}\) in the [EMIM][MeSO3]/water binary solutions can be

extracted by fitting the experimental data \({\gamma }_{{{\rm{H}}}_{2}{\rm{O}}}\,\)to the NRTL equations (Eqs. (3–4)). These parameters are listed in Table 4. In Table 4, the subscript “1”

represents water, while the “2” represents the ionic liquid [EMIM][MeSO3]. \(\Delta {g}_{12-11}\) is the interaction energy change as a result of breaking an H2O-H2O interaction and forming

a [EMIM][MeSO3]-H2O interaction. As shown in Table 4, the interaction energy parameters \(\Delta g\) follow the order [EMIM][MeSO3]-[EMIM][MeSO3] > [EMIM][MeSO3]-H2O ≫ H2O-H2O. The large

negative value of \(\Delta {g}_{12-11}\) indicates that the intermolecular attractive force between [EMIM][MeSO3] and H2O is much stronger than that between H2O and H2O. The absolute value

of interaction energy \(\Delta {g}_{12-11}\) and \(\Delta {g}_{12-22}\) decreases with increasing temperature, which could be attributed to the increasing thermal motion of the

molecules18.

For comparison, the exchange in interaction energy \(\Delta {g}_{12-11}\) and \(\Delta {g}_{12-22}\) in some other ionic liquids/water binary solutions were summarized in Table 5 

19,20,24,25. It should be noted that the \(\Delta {g}_{12-11}\) in the [EMIM][MeSO3]/water binary solution was found to be larger than that in 1-ethyl-3-methylimidazolium ethylsulfate

([EMIM][EtSO4])/water solution25, which is another promising ionic liquid for moisture removal and shares similar chemical structure26,27. The difference in interaction energy may result

from the shorter alkyl group in [EMIM][MeSO3] anion, which is favorable for the bonding with water molecule28,29.

systems.Full size table

The interaction energy between water molecules \({g}_{11}\) is the molar vaporization energy of water (i.e., cohesive energy) but has a negative sign on it30, which is available in

liteature31. The interaction energy between the ionic liquid and water molecules \({g}_{12}\) can be calculated using the formula: \({g}_{12}=\Delta {g}_{12-11}+{g}_{11}\). Similarly, the

interaction energy between the ionic liquid molecules \({g}_{22}\) can be determined by \({g}_{22}=\Delta {g}_{12-22}+{g}_{12}\). The obtained interaction energies \({g}_{11},\,{g}_{12}\)

and \({g}_{22}\) are summarized in Table 4. These molecular interaction energies have negative signs due to the intermolecular attractive forces. It is found in Table 4 that the molecular

interaction energies become less negative when the temperature increases. The magnitude of the interaction energy between the [EMIM][MeSO3] and water molecules was found to be in the range

of 45~49 kJ/mol, which was 20% larger than that between the water molecules in the [EMIM][MeSO3]/water system. The large interaction energy between the ionic liquid [EMIM][MeSO3] and water

molecules can explain many reported macroscopic thermodynamic properties, such as small water activity coefficient and strong hygroscopicity.

The parameters \({\alpha }_{12}\) is related to the non-randomness in the liquid mixture; when \({\alpha }_{12}\) is zero, the local distribution around the center molecule is completely

random. The non-randomness parameters \({\alpha }_{12}\) in the [EMIM][MeSO3]/water binary solutions were found to be around 0.5, as shown in Table 4. The values of α12 are generally

consistent with those reported for other water/hygroscopic ionic liquid binary solutions17,20,24. The non-zero α12 in the [EMIM][MeSO3]/water binary solutions are mainly due to the

difference in interaction energy and size between water and [EMIM][MeSO3].

The extent of the correlation between the experimental data and the NRTL model was evaluated by calculating the absolute relative deviation (ARD)24:

|\frac{{{\rm{\gamma }}}_{\exp }-{{\rm{\gamma }}}_{{\rm{NRTL}}}}{{{\rm{\gamma }}}_{\exp }}|}{{\rm{n}}}$$ (13)

where n is the number of data points, \({\gamma }_{\exp }\) is the γ value calculated from experimental data, and \({\gamma }_{{\rm{NRTL}}}\) is the γ value calculated from the NRTL model.

The values of ARD are also listed in Table 4, which implies a satisfactory correlation in the test temperature range.

One application of these molecular interaction energies is that they can be used to determine the heat of desorption of the aqueous ionic liquid solutions. The internal energy in the aqueous

ionic liquid solution Ul is the sum of the excess internal energy of the solution UE and the molar internal energy of the pure component

Ui:

where n1 and n2 are the mole number of component 1 (i.e., water) and component 2 (i.e., ionic liquid), respectively. In the evaporation process, the intermolecular interaction energy is

dominant, and therefore the intramolecular interaction energy can be neglected in the internal energy. The excess internal energy of the aqueous ionic liquid solution UE can be evaluated

as18,32:

where \({g}_{11}\) and \({g}_{22}\) are the molar interaction energy between water molecules and between the ionic liquid and water molecules, respectively, and \({g}^{(1)}\) and

\({g}^{(2)}\) represent the molar residual Gibbs energy for molecule cells having component 1 and component 2 at the center respectively33. \({g}^{(1)}\) and \({g}^{(2)}\) can be calculated

as:

where x11, x22, x21 and x12 represent the local mole fractions. For example, x21 is the local mole fraction of component 2 around the center component 1. x21 and x12 depend on the global

concentration according to the NRTL model,

{g}_{12-11}/RT)}=\frac{{n}_{2}\ast exp(\,-\,{\alpha }_{12}\Delta {g}_{12-11}/RT)}{{n}_{1}+{n}_{2}\ast exp(\,-\,{\alpha }_{12}\Delta {g}_{12-11}/RT)}$$ (18) $${x}_{12}=\frac{{x}_{1}\ast \exp

(\,-\,{\alpha }_{12}\Delta {g}_{12-22}/RT)}{{x}_{2}+{x}_{1}\ast \exp (\,-\,{\alpha }_{12}\Delta {g}_{12-22}/RT)}=\frac{{n}_{1}\ast \exp (\,-\,{\alpha }_{12}\Delta

{g}_{12-22}/RT)}{{n}_{2}+{n}_{1}\ast \exp (\,-\,{\alpha }_{12}\Delta {g}_{12-22}/RT)}$$ (19)

Differentiating Eq. (14) leads to the change of internal energy in the liquid solution for the evaporation of one mole of water:

{{x}_{2}}^{2}\ast exp(-2{\alpha }_{12}\Delta {g}_{12-11}/RT)}{{({x}_{1}+{x}_{2}\ast exp(-{\alpha }_{12}\Delta {g}_{12-11}/RT))}^{2}}-\frac{\Delta {g}_{12-22}\ast {{x}_{2}}^{2}\ast \exp

(-{\alpha }_{12}\Delta {g}_{12-22}/RT)}{{({x}_{2}+{x}_{1}\ast \exp (-{\alpha }_{12}\Delta {g}_{12-22}/RT))}^{2}}$$ (20)

Considering the volume work in the evaporation process, which is equal to RT based on the ideal gas assumption, the heat of desorption can be calculated using the interaction

energies:

exp(-{\alpha }_{12}\Delta {g}_{12-11}/RT))}^{2}}\\ & & -\,\frac{\Delta {g}_{12-22}\ast {{x}_{2}}^{2}\ast \exp (-\,{\alpha }_{12}\Delta {g}_{12-22}/RT)}{{({x}_{2}+{x}_{1}\ast \exp (-{\alpha

}_{12}\Delta {g}_{12-22}/RT))}^{2}}\end{array}$$ (21)

The formula can be used to predict the heat of desorption in the aqueous binary solutions when the interaction energies are given.

Figure 4 shows the heat of desorption calculated from the interaction energies in the [EMIM][MeSO3]/water binary solutions with water fraction from 0% to 100% at temperatures 303 K, 323 K,

343 K, and 363 K. The desorption heat calculated by the Clausius-Clapeyron Equation is also shown for comparison. As shown in Fig. 4, they are in good agreement. The desorption heat \(\Delta

{H}_{v}\) decreases with increasing temperature for a given water concentration. This trend is consistent with the temperature dependence of the interaction energy parameters \(\Delta

{g}_{12-11}\) and \(\Delta {g}_{12-22}\) listed in Table 4, which could be attributed to the increasing thermal motion of the molecules at elevated temperatures. Due to the strong bonding

forces between water and [EMIM][MeSO3], the desorption heat or enthalpy of vaporization of water in the [EMIM][MeSO3]/water solutions is always higher than the enthalpy of vaporization of

pure water at the same temperature, but the difference becomes smaller when the water concentration approaches 100%.

Desorption heat calculated from the interaction energy in the temperature range of 303 K to 363 K and water fraction range of 0% to 100%. (The desorption heat calculated by the

Clausius-Clapeyron Equation is also shown for comparison).

In this work, molecular thermodynamic properties such as interaction energies and non-randomness parameter of the [EMIM][MeSO3]/water binary system were determined from the water activity

coefficient data using the Non-Random Two-Liquid (NRTL) model. The water activity coefficient of this binary system was measured with molar concentrations of water from 18% to 92% at

temperatures 303 K, 323 K, 343 K, and 363 K. The interaction energy between the ionic liquid [EMIM][MeSO3] and water molecules (\({g}_{12}\)) was found to be ~20% larger than that between

the water molecules (\({g}_{11}\)). The exchange in interaction energy \(\Delta g\) followed the order [EMIM][MeSO3]-[EMIM][MeSO3] > [EMIM][MeSO3]-H2O» H2O-H2O. The large negative value of

\(\Delta {g}_{12-11}\) (−7427.51 J/mol to −7283.79 J/mol) indicated that the intermolecular attractive force between [EMIM][MeSO3] and H2O was much stronger than that between H2O and H2O.

This can explain the observed strong hygroscopicity in the ionic liquid [EMIM][MeSO3]. With the molecular interaction energies, the heat of desorption was predicted in the

[EMIM][MeSO3]/water binary system. The obtained heat of desorption was in good agreement with that calculated from the conventional Clausius-Clapeyron Equation.

All data generated or analyzed during this study are included in this published article.

References Saihara, K., Yoshimura, Y., Ohta, S. & Shimizu, A. Properties of water confined in ionic liquids. Scientific reports 5, 10619 (2015).

Article  ADS  Google Scholar 

Kwon, H.-N., Jang, S.-J., Kang, Y. C. & Roh, K. C. The effect of ILs as co-salts in electrolytes for high voltage supercapacitors. Scientific reports 9, 1180 (2019).

Article  ADS  Google Scholar 

Sun, J., Fu, L. & Zhang, S. A review of working fluids of absorption cycles. Renewable and Sustainable Energy Reviews 16, 1899–1906 (2012).

Article  CAS  Google Scholar 

Wasserscheid, P. & Seiler, M. Leveraging gigawatt potentials by smart heat‐pump technologies using ionic liquids. ChemSusChem 4, 459–463 (2011).

Article  CAS  Google Scholar 

Collier, R., Barlow, R. & Arnold, F. An overview of open-cycle desiccant-cooling systems and materials. Journal of Solar Energy Engineering 104, 28–34 (1982).

Article  CAS  Google Scholar 

Herold, K. E., Radermacher, R. & Klein, S. A. Absorption chillers and heat pumps. (CRC press, 2016).

Krannich, M., Heym, F. & Jess, A. Characterization of six hygroscopic ionic liquids with regard to their suitability for gas dehydration: density, viscosity, thermal and oxidative stability,

vapor pressure, diffusion coefficient, and activity coefficient of water. Journal of Chemical & Engineering Data 61, 1162–1176 (2016).

Article  CAS  Google Scholar 

Krannich, M., Heym, F. & Jess, A. Continuous gas dehydration using the hygroscopic ionic liquid [EMIM][MeSO3] as a promising alternative absorbent. Chemical Engineering & Technology 39,

343–353 (2016).

Article  CAS  Google Scholar 

Stark, A., Zidell, A. W. & Hoffmann, M. M. Is the ionic liquid 1-ethyl-3-methylimidazolium methanesulfonate [emim][MeSO3] capable of rigidly binding water? Journal of Molecular Liquids 160,

166–179 (2011).

Article  CAS  Google Scholar 

Ficke, L. E., Novak, R. R. & Brennecke, J. F. Thermodynamic and thermophysical properties of ionic liquid+ water systems. Journal of Chemical & Engineering Data 55, 4946–4950 (2010).

Article  CAS  Google Scholar 

Hasse, B. et al. Viscosity, interfacial tension, density, and refractive index of ionic liquids [EMIM][MeSO3],[EMIM][MeOHPO2],[EMIM][OcSO4], and [BBIM][NTf2] in dependence on temperature at

atmospheric pressure. Journal of Chemical & Engineering Data 54, 2576–2583 (2009).

Article  CAS  Google Scholar 

Ficke, L. E. & Brennecke, J. F. Interactions of ionic liquids and water. The Journal of Physical Chemistry B 114, 10496–10501 (2010).

Article  CAS  Google Scholar 

Safarov, J., Huseynova, G., Bashirov, M., Hassel, E. & Abdulagatov, I. Viscosity of 1-ethyl-3-methylimidazolium methanesulfonate over a wide range of temperature and Vogel–Tamman–Fulcher

model. Physics and Chemistry of Liquids 56, 703–717 (2018).

Article  CAS  Google Scholar 

Russo, J. W. & Hoffmann, M. M. Measurements of surface tension and chemical shift on several binary mixtures of water and ionic liquids and their comparison for assessing aggregation.

Journal of Chemical & Engineering Data 56, 3703–3710 (2011).

Article  CAS  Google Scholar 

Amado-Gonzalez, E., Esteso, M. A. & Gomez-Jaramillo, W. Mean activity coefficients for NaCl in the mixtures containing ionic liquids [Emim][MeSO3]+ H2O and [Emim][EtSO4]+ H2O at 298.15 K.

Journal of Chemical & Engineering Data 62, 752–761 (2017).

Article  CAS  Google Scholar 

Domańska, U. & Królikowski, M. Measurements of activity coefficients at infinite dilution for organic solutes and water in the ionic liquid 1-ethyl-3-methylimidazolium methanesulfonate. The

Journal of Chemical Thermodynamics 54, 20–27 (2012).

Article  Google Scholar 

Calvar, N., González, B., Gómez, E. & Domínguez, Á. Vapor–liquid equilibria for the ternary system ethanol+ water+ 1-ethyl-3-methylimidazolium ethylsulfate and the corresponding binary

systems containing the ionic liquid at 101.3 kPa. Journal of Chemical & Engineering Data 53, 820–825 (2008).

Article  CAS  Google Scholar 

Schmidt, K., Maham, Y. & Mather, A. Use of the NRTL equation for simultaneous correlation of vapour-liquid equilibria and excess enthalpy: applications to aqueous alkanolamine systems.

Journal of thermal analysis and calorimetry 89, 61–72 (2007).

Article  CAS  Google Scholar 

Döker, M. & Gmehling, J. Measurement and prediction of vapor–liquid equilibria of ternary systems containing ionic liquids. Fluid phase equilibria 227, 255–266 (2005).

Article  Google Scholar 

Wang, J.-F., Li, C.-X., Wang, Z.-H., Li, Z.-J. & Jiang, Y.-B. Vapor pressure measurement for water, methanol, ethanol, and their binary mixtures in the presence of an ionic liquid

1-ethyl-3-methylimidazolium dimethylphosphate. Fluid Phase Equilibria 255, 186–192 (2007).

Article  CAS  Google Scholar 

Koutsoyiannis, D. Clausius–Clapeyron equation and saturation vapour pressure: simple theory reconciled with practice. European Journal of physics 33, 295 (2012).

Article  ADS  Google Scholar 

Henderson-Sellers, B. A new formula for latent heat of vaporization of water as a function of temperature. Quarterly Journal of the Royal Meteorological Society 110, 1186–1190 (1984).

Article  ADS  Google Scholar 

Moffat, R. J. Describing the uncertainties in experimental results. Experimental thermal and fluid science 1, 3–17 (1988).

Article  ADS  Google Scholar 

Zhao, J., Jiang, X.-C., Li, C.-X. & Wang, Z.-H. Vapor pressure measurement for binary and ternary systems containing a phosphoric ionic liquid. Fluid phase equilibria 247, 190–198 (2006).

Article  CAS  Google Scholar 

Zuo, G., Zhao, Z., Yan, S. & Zhang, X. Thermodynamic properties of a new working pair: 1-Ethyl-3-methylimidazolium ethylsulfate and water. Chemical engineering journal 156, 613–617 (2010).

Article  CAS  Google Scholar 

Irfan, M., Rolker, J. & Schneider, R. Process for dehumidifying moist gas mixtures. U.S. Patent Application 15/619,561 (2017).

Zehnacker, O. & Willy, B. Process and absorbent for dehumidifying moist gas mixtures. U.S. Patent 10,105,644 (2018).

Kohno, Y. & Ohno, H. Temperature-responsive ionic liquid/water interfaces: relation between hydrophilicity of ions and dynamic phase change. Physical Chemistry Chemical Physics 14, 5063–5070

(2012).

Article  CAS  Google Scholar 

Kurnia, K. A., Pinho, S. P. & Coutinho, J. A. Designing ionic liquids for absorptive cooling. Green Chemistry 16, 3741–3745 (2014).

Article  CAS  Google Scholar 

Tassios, D. A single-parameter equation for isothermal vapor‐liquid equilibrium correlations. AIChE Journal 17, 1367–1371 (1971).

Article  CAS  Google Scholar 

Cabane, B. & Vuilleumier, R. The physics of liquid water. Comptes Rendus Geoscience 337, 159–171 (2005).

Article  CAS  ADS  Google Scholar 

Sandler, S. I. An introduction to applied statistical thermodynamics. (John Wiley & Sons, 2010).

Renon, H. & Prausnitz, J. M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE journal 14, 135–144 (1968).

Article  CAS  Google Scholar 

Download references

This research is financially supported by DOE under Grant DEEE0008672.

Author informationAuthors and Affiliations University of Maryland, Department of Mechanical Engineering, College Park, MD, 20742, USA

Chaolun Zheng, Jian Zhou, Yong Pei & Bao Yang

AuthorsChaolun ZhengView author publications You can also search for this author inPubMed Google Scholar

Jian ZhouView author publications You can also search for this author inPubMed Google Scholar

Yong PeiView author publications You can also search for this author inPubMed Google Scholar

Bao YangView author publications You can also search for this author inPubMed Google Scholar

B.Y. and C.Z. conceived the experiment and developed the theoretical model. C.Z. set up the experimental system. C.Z. and J.Z. performed the experiments. C.Z. and Y.P. conducted the data

analysis. C.Z. and B.Y. wrote the main manuscript. All authors reviewed the manuscript.

Corresponding author Correspondence to Bao Yang.

The authors declare no competing interests.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this articleCite this article Zheng, C., Zhou, J., Pei, Y. et al. Equilibrium Thermodynamic Properties of Aqueous Solutions of Ionic Liquid 1-Ethyl-3-Methylimidazolium Methanesulfonate

[EMIM][MeSO3]. Sci Rep 10, 3174 (2020). https://doi.org/10.1038/s41598-020-59702-z

Download citation

Received: 21 June 2019

Accepted: 02 December 2019

Published: 21 February 2020

DOI: https://doi.org/10.1038/s41598-020-59702-z

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative