Non-locality correlation in two driven qubits inside an open coherent cavity: trace norm distance and maximum bell function

ABSTRACT We analytically investigate two separated qubits inside an open cavity field. The cavity is initially prepared in a superposition coherent state. The non-locality correlations

[including trace norm measurement induced non-locality, maximal Bell-correlation, and concurrence entanglement] of the two qubits are explored. It is shown that, the generated non-locality

correlations crucially depend on the decay and the initial coherence intensity of the cavity field. The enhancement of the initial coherence intensity and its superposition leads to

increasing the generated non-locality correlations. The phenomena of sudden birth and death entanglement are found. SIMILAR CONTENT BEING VIEWED BY OTHERS SYNCHRONIZATION OF TWO

CAVITY-COUPLED QUBITS MEASURED BY ENTANGLEMENT Article Open access 31 July 2020 QUASI-PROBABILITY INFORMATION IN A COUPLED TWO-QUBIT SYSTEM INTERACTING NON-LINEARLY WITH A COHERENT CAVITY

UNDER INTRINSIC DECOHERENCE Article Open access 06 August 2020 QUANTUM TELEPORTATION AND DYNAMICS OF QUANTUM COHERENCE AND METROLOGICAL NON-CLASSICAL CORRELATIONS FOR OPEN TWO-QUBIT SYSTEMS

Article Open access 22 November 2023 INTRODUCTION Two-level system (qubit) is not only the key element in various fields of the modern physics, such as quantum optics and collision

physics1,2, but also the fundamental building block of modern applications ranging from quantum control3 to quantum processing4. Due to the rapid development of experiments in macroscopic

solid state physics, the artificial two-level atoms qubits based on the superconducting (SC) circuits5,6 and quantum dots (QDs)7 have been recognized as possible candidate for quantum

processing. The SC-qubits have macroscopic quantum coherence. It may be helpful for the realization of the conditional two-qubit gate and quantum hybrid system8,9. Embedding QD-qubits in

microcavities enhances the light extraction efficiency via the Purcell effect and permits the study of cavity QED effects in solid-state systems10,11,12. Experimentally, the qubit-photon

interaction was intensively investigated8,9,13,14,15,16. The dissipation eradicates the useful quantum coherence and correlations17,18. The existence of dissipative qubits, such as in

amorphous solids, is a longstanding problem in solid-state physics19,20. There is a growing interest in the dynamics of non-local correlations (NLCs) beyond the quantum entanglement (QE)21,

which is a unique type that has a major role in quantum processing22. However, QE does not have all of the non-classical properties of the quantum correlations23. While NLCs between the

parts of a system in a pure state is fully characterized by their entanglement, mixed states may possess NLCs even if they are not entangled. New types of NLCs were introduced beyond QE24

as: measurement-induced disturbance25, quantum discord26, and that was determined by using _p_-norms such as; the Hilbert-Schmidt norm, Schatten one-norm and Bures norm. Due to analytic

difficulty to the quantum discord, the geometric correlations appeared via geometric quantum discord (GQD) and the measurement-induced nonlocality (MIN)27 were proposed by using the

2-norm28. However, these measurements that are based on 2-norm have been proved to be incompetent measures of NLC29. Consequently, the GQD and MIN are derived using 1-norm (trace

norm)30,31,32. Moreover, non-classical correlations registered by Bell inequality violation33 (that constitutes one of the most striking phenomena ever observed in nature) is used as an

indicator of non-local quantum properties. While NLCs between the parts of a system in a pure state is fully characterized by their entanglement, mixed states may possess NLCs even if they

are not entangled. Unlike entanglement, quantum discord is rather robust against decoherence34. It is shown that the dynamics of GQD is more robust than the thermal entanglement. Also, the

measures of MINs can be considered as one type of quantum correlation that differs from entanglement and quantum discord30,31,35. Despite the complexity of the suggested model, it is

significant to introduce an analytical description of two optically driven qubits inside an open cavity, that is initially prepared in a coherent state. Therefore, the non-locality

correlations [including, trace norm measurement induced non-locality, maximal Bell-correlation] and the entanglement via the concurrence could be determined. In Sec. 2, the model of

(two-qubit)-cavity system and its analytical solution are introduced. In Sec. 3, the non-locality correlation functions is displayed. We discuss the results of the non-locality correlations

in Sec. 4. Finally, we conclude in Sec. 5. THE PHYSICAL MODEL The studied system is constituted by two sufficiently separated identical artificial two-level atoms (considered as two qubits

_A_ and _B_) resonantly interacting with an open cavity. The two atoms are separated by a distance much larger than their size, consequently their dipole-dipole interplay can be neglected36.

In the rotating wave approximation, the total Hamiltonian is: $$\begin{array}{rcc}\hat{H} & = & {\omega }_{0}{\hat{a}}^{\dagger }\hat{a}+{\omega }_{0}\sum _{i=A,B}{\hat{\sigma

}}_{i}^{z}+\sum _{i=A,B}({\lambda }_{i}\hat{a}{\hat{\sigma }}_{i}^{-}+{\lambda }_{i}^{\ast }{\hat{a}}^{\dagger }{\hat{\sigma }}_{i}^{+}),\end{array}$$ (1) where _ω_0 represent the qubits and

the cavity frequency. \({\hat{a}}^{\dagger }\) and \(\hat{a}\) are respectively the creation and annihilation operators of the cavity mode. The operators \({\hat{\sigma }}_{i}^{\pm }\) and

\({\hat{\sigma }}_{i}^{z}\) are the Pauli matrices which are defined by the upper states |1〉_i_, and lower states |0〉_i_. _λ__i_ designate the coupling between the cavity and the qubits.

Here, we focus on the case where _λ__i_ = _λ_. If we consider only the dissipative term of the dipole decay of the qubits, the dynamic of the system is given by37

$$\begin{array}{rcl}\frac{\partial \hat{\rho }(t)}{\partial t} & = & -i[\hat{H},\hat{\rho }(t)]\\ & & +\sum _{i=A,B}{\gamma }_{i}([{\hat{\sigma }}_{i}^{-},\hat{\rho

}(t){\hat{\sigma }}_{i}^{+}]+[{\hat{\sigma }}_{i}^{-}\hat{\rho }(t),{\hat{\sigma }}_{i}^{+}]),\end{array}$$ (2) where _γ__i_ are spontaneous emission rates of the two qubits, which are

treated by coupling each qubit to reservoir. In the basis states {|1〉 = |1_A_1_B_, _n_〉, |2〉 = |1_A_0_B_, _n_ + 1〉, |3〉 = |0_A_1_B_, _n_+1〉, |4〉 = |0_A_0_B_, _n_ + 2〉}, the dressed states,

|Ψ_i__m_〉(_i_ = 1–4), are $$\,(\begin{array}{c}|{\varPsi }_{1}^{n}\rangle \\ |{\varPsi }_{2}^{n}\rangle \\ |{\varPsi }_{3}^{n}\rangle \\ |{\varPsi }_{4}^{n}\rangle

\end{array})=A(\begin{array}{c}\mathrm{|1}\rangle \\ \mathrm{|2}\rangle \\ \mathrm{|3}\rangle \\ \mathrm{|4}\rangle \end{array}),A=(\begin{array}{cccc}{\tilde{a}}_{n} & 0 & 0 &

-{\tilde{b}}_{n}\\ 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0\\ {b}_{n} & -\frac{1}{2} & -\frac{1}{2} & {a}_{n}\\ {b}_{n} & \frac{1}{2} & \frac{1}{2}

& {a}_{n}\end{array})\mathrm{}.$$ (3) where \({a}_{n}=\sqrt{\frac{n+2}{2(2n+3)}},\,{b}_{n}=\sqrt{\frac{n+1}{2(2n+3)}}\) and \(\tilde{a}{(\tilde{b})}_{n}=a{(b)}_{n}\sqrt{2}\). In the case

of high −_Q_ cavity (\({\gamma }_{i}\ll {\lambda }_{i}\)), we apply the dressed-states representation (DSR) based on the Hamiltonian eigenstates38,39,40. The operators of the qubits,

|1〉_ii_〈0|, of Eq. (7) are written in the DSR. In this paper we focus on the case where the two qubits are initially in the excited state (uncorrelated state), i.e., \({\hat{\rho

}}_{AB}(0)\) = |1_A_1_B_〉〈1_A_1_B_|. While the wave function of cavity mode field is initially prepared in the superposition coherent state: |_α_〉 + _κ_|−_α_〉, where _α_ is the intensity of

the coherent state, i.e., $$\begin{array}{rcl}\,{\hat{\rho }}_{F}(0) & = & \sum _{m,n=0}{Q}_{m,n}|m\rangle \langle n|,\\ & = & \frac{[1+\kappa {(-1)}^{m}][1+\kappa

{(-1)}^{n}]}{[1+{\kappa }^{2}+2\kappa {e}^{-2N}]\sqrt{m!n!}}{N}^{\frac{m+n}{2}}{e}^{-N}|m\rangle \langle n|.\end{array}$$ (4) _N_ = |_α_|2 designs the mean photon number and _κ_ = 0 and 1

are taken respectively for the coherent state and the superposition coherent state. Coherent states and their superpositions are proposed as major elements for the realization of quantum

processing. Using the dressed states space, {|Ψ_i__m_〉}, of Eq. (3), the initial total density matrix in DSR is rewritten as: $$\begin{array}{ccc}\,W(0) & = & \sum

_{m,n=0}2{f}_{aa}|{\Psi }_{1}^{m}\rangle \langle {\Psi }_{1}^{n}|+{f}_{ba}^{mn}\sqrt{2}[{\hat{h}}_{31}^{mn}+{\hat{h}}_{41}^{mn}]\\ & &

+{f}_{bb}^{mn}[{\hat{h}}_{33}^{mn}+{\hat{h}}_{34}^{mn}+{\hat{h}}_{43}^{mn}+{\hat{h}}_{44}^{mn}]+{f}_{ab}^{mn}\sqrt{2}[{\hat{h}}_{13}^{mn}|+{\hat{h}}_{14}^{mn}],\end{array}$$ (5) where

_f__rs__mn_ = _Q__m_,_n__r__m__s__n_(_r_, _s_ = _a_, _b_), \({\hat{h}}_{kl}^{mn}\) = |Ψ_k__n_〉〈Ψ_l__n_|. In the basis states of the two qubits {|1〉 = |1_A_1_B_, _n_〉, |2〉 = |1_A_0_B_, _n_ + 

1〉, |3〉 = |0_A_1_B_, _n_ + 1〉, |4〉 = |0_A_0_B_, _n_ + 2〉}, Eq. 2 becomes $$\hat{\rho }(t)=\mathop{\sum }\limits_{ij=0}^{4}\mathop{\sum }\limits_{mn=0}^{\infty }{\langle

i|{e}^{-i\hat{H}t}W(t){e}^{i\hat{H}t}|j\rangle }_{mn}(t)\,|i\rangle \langle j|\mathrm{}.$$ (6) To calculate \({\langle i|{e}^{-i\hat{H}t}W(t){e}^{i\hat{H}t}|j\rangle }_{mn}(t)\), we used the

following canonical transform; \(W(t)={e}^{i\hat{H}t}\hat{\rho }(t){e}^{-i\hat{H}t}\) in Eq. (7) to became: $$\dot{W}(t)=\sum _{i=A,B}{\gamma }_{i}{e}^{i\hat{H}t}([{\hat{\sigma

}}_{i}^{-},\hat{\rho }(t){\hat{\sigma }}_{i}^{+}]+[{\hat{\sigma }}_{i}^{-}\hat{\rho }(t),{\hat{\sigma }}_{i}^{+}]){e}^{-i\hat{H}t}\mathrm{}.$$ (7) If _i_ ≠ _j_, the elements

〈Ψ_k__i_|_W_(_t_)|Ψ_l__j_〉 are calculated from $$\langle {\Psi }_{k}^{i}|W(t)|{\Psi }_{l}^{j}\rangle ={e}^{-({\gamma }_{A}+{\gamma }_{B}){\beta }_{kl}t}\langle {\Psi

}_{k}^{i}|W\mathrm{(0)|}{\Psi }_{l}^{j}\rangle ,$$ (8) with \({\beta }_{12}^{ij}={\beta }_{21}^{ji}=(2{a}_{i}^{2}+\frac{1}{2})\), \({\beta }_{23}^{ij}={\beta }_{32}^{ji}={\beta

}_{24}^{ij}={\beta }_{42}^{ji}=({b}_{j}^{2}+\frac{3}{4})\), _β_22_ij_ = 1, \({\beta }_{13}^{ij}={\beta }_{31}^{ji}={\beta }_{41}^{ij}={\beta }_{14}^{ji}=\)

\((2{a}_{i}^{2}+{b}_{j}^{2}+\frac{1}{4})\) and \({\beta }_{33}^{ij}={\beta }_{34}^{ij}={\beta }_{43}^{ij}={\beta }_{44}^{ij}=({b}_{i}^{2}+{b}_{j}^{2}+\frac{1}{2})\). While, if _i_ = _j_, the

elements 〈Ψ_k__i_|_W_(_t_)|Ψ_l__i_〉 are calculated from $$\begin{array}{rcl}{\dot{A}}_{i} & = & 2\gamma {b}_{i}^{2}{B}_{i+1}+\gamma {b}_{i}^{2}{C}_{i+1}-4\gamma

{a}_{i}^{2}\,{A}_{i},\\ {\dot{B}}_{i} & = & 2\gamma {a}_{i+1}^{2}{A}_{i+1}+\gamma {b}_{i+1}^{2}{C}_{i+1}-\gamma {B}_{i},\\ {\dot{C}}_{i} & = & 2\gamma

{a}_{i+1}^{2}{A}_{i+1}+2\gamma {a}_{i}^{2}{B}_{i+1}+2\gamma {\chi }_{i+1}{C}_{i+1}-\gamma {\varphi }_{i}{C}_{i}.\end{array}$$ (9) where _γ_ = _γ__A_ + _γ__B_, _A__i_ = 

〈Ψ1_i_|_W_(_t_)|Ψ1_i_〉, _B__i_ = 〈Ψ2_i_|_W_(_t_)|Ψ2_i_〉, _C__i_ = 〈Ψ3_i_|_W_(_t_)|Ψ3_i_〉 + 〈Ψ4_i_|_W_(_t_)|Ψ4_i_〉, \({\chi }_{i+1}=\frac{1}{2}({a}_{i}^{2}+{b}_{i+1}^{2})\) and \({\varphi

}_{i}=2{b}_{i}^{2}+\frac{1}{2}\). The Eq. (9) is exactly solvable for the case where each state has at most _N_ photons only, i.e, _A__N_+1 = _B__N_+1 = _C__N_+1 = 0, the case _N_ → ∞ could

be considered38. Equation (9) gives at _i_ = _N_, $$\begin{array}{rcl}{A}_{i}(t) & = & {e}^{-4\gamma {a}_{i}^{2}t}[{A}_{i}\mathrm{(0)}+\gamma {b}_{i}^{2}{\int

}_{0}^{t}[2{B}_{i+1}+{C}_{i+1}]{e}^{4\gamma {a}_{i}^{2}t}dt],\\ {B}_{i}(t) & = & {e}^{-\gamma t}[{B}_{i}\mathrm{(0)}+\,\gamma {\int

}_{0}^{t}\,[2{a}_{i+1}^{2}{A}_{i+1}+{b}_{i+1}^{2}{C}_{i+1}]{e}^{\gamma t}dt],\\ {C}_{i}(t) & = & {e}^{-\gamma {\varphi }_{i}t}[{C}_{i}\mathrm{(0)}+2\gamma {\int

}_{0}^{t}[{a}_{i+1}^{2}{A}_{i+1}+{a}_{i}^{2}{B}_{i+1}+{\chi }_{i+1}{C}_{i+1}]{e}^{\gamma {\varphi }_{i}t}dt].\end{array}$$ (10) Therefore \({A}_{N}(t)={e}^{-4\gamma

{a}_{i}^{2}t}{A}_{N}(0),\,{B}_{N}(t)={e}^{-\gamma t}{B}_{N}(0),\,{C}_{N}(t)={e}^{-\gamma {\varphi }_{N}t}{C}_{N}(0)\). at _i_ = _N_ − 1, we get $$\begin{array}{rcl}{A}_{N-1}(t) & = &

{e}^{-4\gamma {a}_{N-1}^{2}t}[{A}_{N-1}\mathrm{(0)}\\ & & +\gamma {b}_{N-1}^{2}{\int }_{0}^{t}\mathrm{[2}{B}_{N}+{C}_{N}]{e}^{4\gamma {a}_{N-1}^{2}t}dt],\\ {B}_{N-1}(t) & =

& {e}^{-\gamma t}[{B}_{N-1}\mathrm{(0)}+\gamma {\int }_{0}^{t}\mathrm{[2}{a}_{N}^{2}{A}_{N}+{b}_{N}^{2}{C}_{N}]{e}^{\gamma t}dt],\\ {C}_{N-1}(t) & = & {e}^{-\gamma {\varphi

}_{N-1}t}[{C}_{N-1}\mathrm{(0)}+2\gamma {\int }_{0}^{t}[{a}_{N}^{2}{A}_{N}+{a}_{i}^{2}{B}_{N}+{\chi }_{N}{C}_{N}]{e}^{\gamma {\varphi }_{N-1}t}dt].\end{array}$$ Then we can calculate for _i_

 = _N_ − 2, _N_ − 3, ..., 0. The density operator of the qubits _ρ__AB_(_t_) can be determined, by tracing the cavity field degrees of freedom as: $${\rho }^{AB}(t)={{\rm{tr}}}_{F}\{\rho

(t)\}=\mathop{\sum }\limits_{k\mathrm{=0}}^{\infty }\langle k|\rho (t)|k\rangle \mathrm{}.$$ (11) Now, we can explore the time evolution of the non-local correlations. NON-LOCALITY AND

CONCURRENCE QUANTIFIERS We adopt as non-locality quantifiers: the trace norm measurement induced non-locality (MIN) and the Bell function. These measures will be compared to the concurrence

as a quantifier of entanglement. CONCURRENCE The concurrence41 is one of the most used measures of the entanglement between two qubits. It is defined as, $$C(t)=\,{\rm{\max

}}\{0,\sqrt{{\lambda }_{1}}-\mathop{\sum }\limits_{i=2}^{4}\,\sqrt{{\lambda }_{i}}\};\,{\lambda }_{i} > {\lambda }_{i+1},$$ (12) where _λ__i_ are the eigenvalues of the following matrix:

$$T={\rho }^{AB}(t)({\sigma }_{y}\otimes {\sigma }_{y}){\rho }^{\ast AB}(t)({\sigma }_{y}\otimes {\sigma }_{y}).$$ TRACE-NORM MIN Firstly, the measurement induced non-locality for a

two-qubit state _ρ__AB_(_t_) is defined via Hilbert-Schmidt norm (2-norm)27. Unfortunately, just like geometric quantum discord based on 2-norm, it may change under trivial local reversible

operations on an unmeasured subsystem of _ρ__AB_(_t_)29. To address this issue, the MIN based on trace norm (1-MIN) and others have been introduced by30,31,32. The modified versions of the

_p_-MIN based on the Schatten _p_-norm is given by30,31 $${M}_{p}({\rho }^{AB}(t))=\mathop{{\rm{\max }}}\limits_{\chi \in {\varPi }^{A}}{\Vert {\rho }^{AB}(t)-{\Pi }^{A}({\rho

}^{AB}(t))\Vert }_{p}^{p}.$$ (13) where \({\Vert A\Vert }_{p}\) is the Schatten _p_-norm of a matrix/vector _A_. Here we use 1-MIN that represents the maximal trace distance between the

pre-measurement state and the post-measurement state caused by the locally invariant measurements. the trace-norm MIN in explicit form can be written as:

$$M(t)=\{\begin{array}{cc}\frac{\sqrt{{\chi }_{+}}+\sqrt{{\chi }_{-}}}{2{\Vert \overrightarrow{{\rm{x}}}\Vert }_{1}}, & {\rm{If}}\,\overrightarrow{{\rm{x}}}\ne \mathrm{0;}\\ 2\,{\rm{\max

}}\,\{|{r}_{11}|,|{r}_{22}|,|{r}_{33}|\}, & {\rm{If}}\,\overrightarrow{{\rm{x}}}=0.\end{array}$$ (14) where \({\chi }_{\pm }=\alpha \pm 2\sqrt{\beta }{\Vert

\overrightarrow{{\rm{x}}}\Vert }_{1}\), \(\alpha ={\Vert C\Vert }_{2}^{2}{\Vert x\Vert }_{1}^{2}-{\sum }_{i}\,{r}_{ii}^{2}{x}_{i}^{2}\), _C_ = [_r__ii_] and \(\beta ={\sum }_{\langle

ijk\rangle }{x}_{i}^{2}{r}_{jj}^{2}{r}_{kk}^{2}\), the summation of _β_ runs over all the cyclic permutations of 1,2,3. where where _x__i_ = _Tr_(_ρ__AB__(t_)(_σ__i_ ⊗ _I_)) are the elements

of the local Bloch vector _x_, while, _r__mn_ = _tr_{_ρ__AB__(t_)(_σ__m_ ⊗ _σ__n_)} represent the components of the correlation matrix _R_ = [_r__mn_]28. \(\overrightarrow{\sigma }=({\sigma

}_{1},{\sigma }_{2},{\sigma }_{3})\) represents a vector of the Pauli spin matrices. If the elements of density matrix _ρ__AB_(_t_) are denoted by: _z__ij_ = 〈_i_|_ρ__AB_(_t_)|_j_〉 = 

_e__ij_ + _id__ij_, then $$\overrightarrow{{\rm{x}}}={({e}_{13}+{e}_{24},{d}_{31}+{d}_{42},{z}_{11}+{z}_{22}-1/2)}^{t},$$ (15) while, the correlation matrix _R_ for a general bipartite

quantum state _ρ__AB_(_t_) is given by $${\bf{R}}=(\begin{array}{ccc}{e}_{23}+{e}_{14} & {d}_{23}-{d}_{14} & {e}_{13}-{e}_{24}\\ {d}_{41}-{d}_{23} & {e}_{23}-{e}_{14} &

{d}_{13}+{d}_{24}\\ {e}_{12}-{e}_{34} & {d}_{34}-{d}_{12} & {z}_{11}+{z}_{44}-\frac{1}{2}\end{array})\mathrm{}.$$ (16) (II) - MAXIMUM BELL FUNCTION: The maximal value of the Bell

function _B__max_(_t_), is considered as an indicator of non-locality correlation33. If _B_max(_t_) > 2, then the Bell’s inequality is violated, i.e., _B_max(_t_) locates the nonlocal

quantum correlations when its value is above 2 (the classical threshold). Here, we use the Bell function defined by $$B(t)=2\sqrt{{S}_{{\rm{\max }}}}-1,$$ (17) where, _S_max is the summation

of the two largest eigenvalues for the matrix \(U={{\rm{R}}}^{\dagger }{\rm{R}}\), R represents the correlation matrix of a two-qubit state _ρ__AB_. The function _B_(_t_) identifies NLC

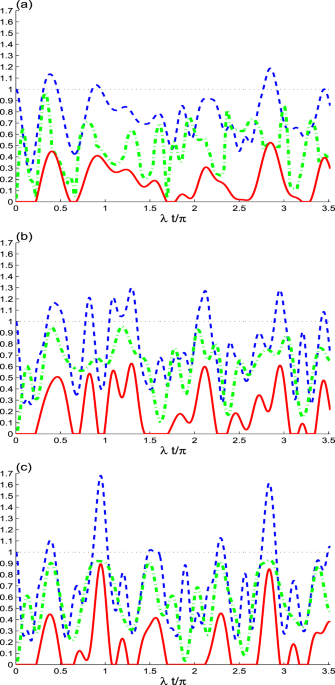
when it is above the classical threshold 1. NLC DYNAMICS EFFECT OF THE COHERENT CAVITY SUPERPOSITION In Fig. 1, we display the resulted non-locality correlations of the two qubits with

respect to the unitary interaction _γ_ = 0. Where the trace-norm MIN, _M_(_t_), maximal Bell function, _B_(_t_), and the concurrence _C_(_t_) are displayed for different values of the

superposition parameter _κ_ = 0; _κ_ = 0 in (a), _κ_ = 1 in (b) and _κ_ = −1 in (c) with the initial coherence intensity _N_ = 2. From a chosen initial pure state of the qubits |1_A_1_B_〉 or

|0_A_0_B_〉, the elements of the correlation matrix R are zero except for _r_33 = 1, and the Bloch vector is _x_ = (0, 0, ±1)_t_ ≠ 0. Therefore, _M_(0) = 0, _B_(0) = 1, and _C_(0) = 0, i.e,

the state of the qubits does not have correlations. If the pure state of the qubits develops to one of the maximal correlated states, \(\frac{1}{2}\mathrm{(|01}\rangle \pm

\mathrm{|10}\rangle )\), the elements the correlation matrix _R_ are zero except for the element _r_11 = ±0.5, _r_22 = ±0.5 and _r_33 = −0.5, and the Bloch vector is _x_ = (0, 0, 0)_t_.

Therefore, _M_(0) = 1, _B_(0) = 1.8284, and _C_(0) = 1 (generating maximal NLCs). Otherwise, the qubits-cavity interaction generates partial correlations. In Fig. 1a, we consider the initial

coherent state _κ_ = 0 while the dipole decay of the qubits is neglected (_γ_ = 0). We observe that the unitary interaction leads to: (1) the uncorrelated state of the qubits, |1_A_1_B_〉,

produces an oscillatory partial entanglement and non-locality correlations during the time evolution of the qubits-cavity interaction. These partial correlations are enhanced with increasing

the interaction time. As the unitary interaction evolves, the concurrence _C_(_t_) is zero for a short time, and it suddenly grows to its partial maximum value at particular points. These

points are called growth-start points (GSPs). _C_(_t_) presents sudden birth and death entanglement42. (2) the trace-norm MIN _M_(_t_) grows from zero (i.e., GSP is zero) to its partial

maximum values. It has different behaviour compared to _C_(_t_). _M_(_t_) never vanishes. The upper bounds of trace-norm MIN are larger than that of the concurrence. (3) with respect to

_B_(_t_), we observe that the Bell’s inequality is violated for short time intervals, in which _B_(_t_) > 1. Where, in the case of _κ_ = −1, the values of NLC functions may reach

approximately the values of the maximal correlated states, \(\frac{1}{2}\mathrm{(|01}\rangle \pm \mathrm{|10}\rangle )\), that are mentioned above. This mean that there is relation between

the correlation dynamics and the evolution of the state of the qubits. In Fig. 1b,c, the dependence of the NLCs on the superposition of coherent states parameter _κ_ is depicted. The NLC

functions for the two cases of the initial even coherent state _κ_ = 1 in (b) and the initial odd coherent state _κ_ = −1 in (c) are simulated with the same data of Fig. 1a. We observe that

the generated NLCs are bigger compared to the ones of the coherent cavity. The superposition of the coherent state parameter _κ_ leads to the increase of the time intervals of the maximal

violation of Bell’s inequality of _B_(_t_) > 1. EFFECT OF THE DIPOLE QUBITS DECAY In Fig. 2, the NLC functions _M_(_t_), _B_(_t_), and _C_(_t_) are plotted for the initial coherent state

_κ_ = 0 and the dipole decay of qubits (_γ_ = 0.08_λ_). We note a more rapid deterioration of the non-local correlations. In case of coherent cavity field _κ_ = 0 with _γ_/_λ_ = 0.08, we

observe: (1) due to the dipole decay of the qubits, the two functions of maximal Bell function and the concurrence vanish approximately whereas the trace norm MIN function does not vanish.

For the cases of the initial even coherent _κ_ = 1 and odd coherent _κ_ = −1 microcavity field, we observe that the oscillations, amplitudes and the negativity of the NLC functions _M_(_t_),

_B_(_t_), and _C_(_t_) are more robust against the rate of dipole qubits decay _γ_/_λ_, (see Fig. 2b,c). Therefore, the generated NLCs depend on the dipole decay and on the initial coherent

cavity field. Due to the dipole qubits decay, the stable state of the two qubits has a value of the trace norm MIN correlation beyond that of entanglement and non-locality Bell-correlation.

EFFECT OF THE INITIAL COHERENCE INTENSITY In Fig. 3, we analyze the effect of the initial coherence intensity _N_, where _N_ = 0.5 is small and the dipole decay of qubits is neglected. We

notice the change of the dynamical behavior of the NLCs. We observe that the NLC functions _M_(_t_), _B_(_t_), and _C_(_t_) (see Figs. 1 and 3) exhibit extreme values and amplitudes less

than that of _N_ = 2. The Bell’s inequality is violated during short intervals, for the initial even coherent _κ_ = 1 and odd coherent _κ_ = −1 cavity field. However, for a coherent state

there is no violation of the Bell’s inequality is observed. We deduce that the amount of the generated entanglement and non-locality correlations may be increased by increasing the initial

coherence intensity _N_. Figure 4 shows the effect of the dipole decay _γ_ = 0.08_λ_ on NLCs between the two qubits. We observe that the NLCs for _γ_ = 0.05_λ_ have damped oscillations,

their amplitudes decrease until completely vanish. When the dipole decay is increased, reduction of the final disappearance time of the NCLs is noted. For the small initial coherence

intensity, _N_ = 0.5 (see Fig. 4b), _C_(_t_) is quasi-periodic. The sudden birth and death entanglement is observed for large time windows. The generated NLCs are weak and has less

robustness as the initial coherence intensity decreases. The NLCs are reduced by the decrease of the initial coherence. The extreme values of trace norm MIN is more robust than the

entanglement and non-locality Bell-correlation. CONCLUSION Throughout this paper, an analytical description of a cavity contains two qubits spatially separated is established. The

non-locality correlations [including trace norm measurement induced non-locality, maximal Bell-correlation and concurrence entanglement] of the two qubits are explored via the trace norm

measurement induced non-locality and the Maximum Bell function. The rise in two-qubit damping rates induces a fast deterioration of the coherence. We notice that this system presents sudden

birth and death entanglement. The generated non-locality correlations essentially determined by the loss rate of the two-qubit and the initial coherence of the cavity. REFERENCES * Shore, B.

W. _The Theory of Coherent Atomic Excitation_ (Wiley, New York, 1990). * Li, D. X. & Shao, X. Q. Rapid population transfer of a twolevel system by a polychromatic driving field. _Sci.

Rep._ 9, 9023 (2019). Article  ADS  CAS  Google Scholar  * Nakamura, Y., Pashkin, Y. A. & Tsai, J. S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. _Nature_

398, 786 (1999). Article  ADS  CAS  Google Scholar  * Treutlein, P., Genes, C., Hammerer, K., Poggio, M. & Rabl, P. _Hybrid Mechanical Systems_ (Springer Berlin Heidelberg, 2014). *

Kang, Y. H. _et al_. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. _Sci. Rep._ 6, 36737 (2016). Article  ADS  CAS  Google Scholar  * Khan, S.

& Tureci, H. E. Frequency Combs in a Lumped-Element Josephson-Junction Circuit. _Phys. Rev. Lett._ 120, 153601 (2018). Article  ADS  CAS  Google Scholar  * Nilsen, M. A. & Chuang, I.

L. _Quantum Computation and Quantum Information_ (Cambridge: Cambridge University Press 2000). * Kielpinski, D., Kafri, D., Woolley, M. J., Milburn, G. J. & Taylor, J. M. Quantum

Interface between an Electrical Circuit and a Single Atom. _Phys. Rev. Lett._ 108, 130504 (2012). Article  ADS  CAS  Google Scholar  * Motte, D. D. _et al_. Experimental system design for

the integration of trapped-ion and superconducting qubit systems. _Quantum Inf. Process._ 15, 5385 (2016). Article  ADS  Google Scholar  * Reitzenstein, S. Semiconductor Quantum

Dot–Microcavities for Quantum Optics in Solid State. _IEEE J. Sel. Top. Quantum Electron._ 18, 1733 (2012). Article  ADS  CAS  Google Scholar  * Cygorek, M., Barth, A. M., Ungar, F., Vagov,

A. & Axt, V. M. Nonlinear cavity feeding and unconventional photon statistics in solid-state cavity QED revealed by many-level real-time path-integral calculations. _Phys. Rev. B_ 96,

201201(R) (2017). Article  ADS  Google Scholar  * Feng, M., D’Amico, I., Zanardi, P. & Rossi, F. Spin-based quantum-information processing with semiconductor quantum dots and cavity QED.

_Phys. Rev. A_ 67, 014306 (2003). Article  ADS  Google Scholar  * Kremer, P. E. _et al_. Strain-tunable quantum dot embedded in a nanowire antenna. _Phys. Rev. B_ 90, 201408 (2014). Article

  ADS  Google Scholar  * Hanschke, L. _et al_ Quantum dot single-photon sources with ultra-low multiphoton probability. _npj Quantum Information_ 4(2018) 43. * Liu, Y.-x, You, J. Q., Wei, L.

F., Sun, C. P. & Nori, F. Optical selection rules and phase-dependent adiabatic state control in a superconducting quantum circuit. _Phys. Rev. Lett._ 95, 087001 (2005). Article  ADS 

Google Scholar  * Yoshihara, F. _et al_. Inversion of Qubit Energy Levels in Qubit-Oscillator Circuits in the Deep-Strong-Coupling Regime. _Phys. Rev. Lett._ 120, 183601 (2018). Article  ADS

  CAS  Google Scholar  * Abdel-Aty, M. A qualitative perspective on the dynamics of a single-Cooper-pair box with a phase-damped cavity. _J. Phys. A_ 41, 185304 (2008). Article  MathSciNet 

Google Scholar  * Sete, E. A., Eleuch, H. & Ooi, C. H. R. Light-to-matter entanglement transfer in optomechanics. _J. Opt. Soc. Am B_ 31, 2821 (2014). Article  ADS  CAS  Google Scholar 

* Philips, W. A. Two-level states in glasses. _Rep. Prog. Phys._ 50, 1657 (1987). Article  ADS  Google Scholar  * Gordon, L., Abu-Farsakh, H., Janotti, A. & Van de Walle, G. Hydrogen

bonds in Al2O3 as dissipative two-level systems in superconducting qubits. _Sci. Rep._ 4, 7590 (2014). Article  CAS  Google Scholar  * Mohamed, A.-B. A. & Eleuch, H. Non-classical

effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. _Eur. Phys. J. D_ 69, 191 (2015). Article  ADS  Google Scholar  * Aolita, L.,

deMelo, F. & Davidovich, L. Open-system dynamics of entanglement: a key issues review. _Rep. Prog. Phys._ 78, 042001 (2015). Article  ADS  Google Scholar  * Sete, E. A. & Eleuch, H.

Strong squeezing and robust entanglement in cavity electromechanics. _Phys. Rev. A_ 89, 013841 (2014). Article  ADS  Google Scholar  * Clauser, J. F., Horne, M. A. & Shimony, A.

Proposed Experiment to Test Local Hidden-Variable Theories. _Phys. Rev. Lett._ 23, 880 (1969). Article  ADS  Google Scholar  * Luo, S. Using measurement-induced disturbance to characterize

correlations as classical or quantum. _Phys. Rev. A_ 77, 022301 (2008). Article  ADS  Google Scholar  * Ollivier, H. & Zurek, W. H. Quantum Discord: A Measure of the Quantumness of

Correlations. _Phys. Rev. Lett._ 88, 017901 (2001). Article  ADS  Google Scholar  * Luo, S. & Fu, S. Measurement-Induced Nonlocality. _Phys. Rev. Lett._ 106, 120401 (2011). Article  ADS

  Google Scholar  * Dakic, B., Vedral, V. & Brukner, C. Necessary and Sufficient Condition for Nonzero Quantum Discord. _Phys. Rev. Lett._ 105, 190502 (2010). Article  ADS  Google

Scholar  * Piani, M. Problem with geometric discord. _Phys. Rev. A_ 86, 034101 (2012). Article  ADS  Google Scholar  * Hu, M. L. & Fan, H. Measurement-induced nonlocality based on the

trace norm. _New J. Phys._ 17, 033004 (2015). Article  ADS  Google Scholar  * Hu, M.-L. _et al_. Quantum coherence and geometric quantum discord. _Phys. Rep._ 762, 1 (2018). ADS  MathSciNet

  MATH  Google Scholar  * Paula, F. M., de Oliveira, T. R. & Sarandy, M. S. Geometric quantum discord through the Schatten 1-norm. _Phys. Rev. A_ 87, 064101 (2013). Article  ADS  Google

Scholar  * Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. _Rev. Mod. Phys._ 86, 419 (2014). Article  ADS  Google Scholar  * Mazzola, L., Piilo, J.

& Maniscalco, S. Sudden Transition between Classical and Quantum Decoherence. _Phys. Rev. Lett._ 104, 200401 (2010). Article  ADS  MathSciNet  CAS  Google Scholar  * Ma, Y.-X., Li, L.

& Hou, X.-W. Quantum nonlocality in the spin-s Heisenberg models with the Dzyaloshinskii–Moriya interaction. _Quantum Inf. Process._ 18, 288 (2019). Article  ADS  MathSciNet  Google

Scholar  * Unold, T., Mueller, K., Lienau, C., Elsaesser, T. & Wieck, A. D. Optical Control of Excitons in a Pair of Quantum Dots Coupled by the Dipole-Dipole Interaction. _Phys. Rev.

Lett._ 94, 137404 (2005). Article  ADS  Google Scholar  * Puri, R. R. _Mathematical Methods of Quantum Optics_. 252 (Springer-Verlag, Berlin, 2001). * Barnett, S. M. & Knight, P. L.

Dissipation in a fundamental model of quantum optical resonance. _Phys. Rev. A_ 33, 2444 (1986). Article  ADS  CAS  Google Scholar  * Bashkirov, E. K. & Rusakova, M. S. Statistics and

light squeezing in the dissipative two-atom Jaynes-Cummings model. _Optics and Spectroscopy_ 105, 73 (2008). Article  ADS  CAS  Google Scholar  * Bashkirov, E. K. Collective radiation of a

system of two three-level V-type atoms in a two-mode resonator with losses. _Rus. Phys. J._ 49, 207 (2006). Article  Google Scholar  * Wootters, W. K. Entanglement of Formation of an

Arbitrary State of Two Qubits. _Phys. Rev. Lett._ 80, 2245 (1998). Article  ADS  CAS  Google Scholar  * Yu, T. & Eberly, J. H. Finite-Time Disentanglement Via Spontaneous Emission.

_Phys. Rev. Lett._ 93, 140404 (2004). Article  ADS  Google Scholar  Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Mathematics, College of Science and

Humanities in Al-Aflaj, Prince Sattam bin Abdulaziz University, Al-Aflaj, Saudi Arabia A. -B. A. Mohamed * Faculty of Science, Assiut University, Assiut, Egypt A. -B. A. Mohamed * Department

of Applied Sciences and Mathematics, College of Arts and Sciences, Abu Dhabi University, Abu Dhabi, UAE H. Eleuch * Institute for Quantum Science and Engineering, Texas A&M University,

College Station, Texas, 77843, USA H. Eleuch * Department of Physics, University of Malaya, 50603, Kuala Lumpur, Malaysia C. H. Raymond Ooi Authors * A. -B. A. Mohamed View author

publications You can also search for this author inPubMed Google Scholar * H. Eleuch View author publications You can also search for this author inPubMed Google Scholar * C. H. Raymond Ooi

View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.-B.A. Mohamed prepared all Figures and performed the mathematical calculations. H. Eleuch

and C.H. Raymond Ooi. analyzed the non-locality correlation. All authors contributed to discussions of the paper. CORRESPONDING AUTHOR Correspondence to A. -B. A. Mohamed. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mohamed, A.B.A., Eleuch, H. & Ooi, C.H.R. Non-locality Correlation in Two Driven Qubits Inside an Open Coherent Cavity: Trace Norm

Distance and Maximum Bell Function. _Sci Rep_ 9, 19632 (2019). https://doi.org/10.1038/s41598-019-55548-2 Download citation * Received: 28 March 2019 * Accepted: 07 October 2019 * Published:

23 December 2019 * DOI: https://doi.org/10.1038/s41598-019-55548-2 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative