Differential electron emission from polycyclic aromatic hydrocarbon molecules under fast ion impact

ABSTRACT Interaction between polycyclic aromatic hydrocarbon (PAH) molecule and energetic ion is a subject of interest in different areas of modern physics. Here, we present measurements of

energy and angular distributions of absolute double differential electron emission cross section for coronene (C24H12) and fluorene (C13H10) molecules under fast bare oxygen ion impact. For

coronene, the angular distributions of the low energy electrons are quite different from that of simpler targets like Ne or CH4, which is not the case for fluorene. The behaviour of the

higher electron energy distributions for both the targets are similar to that for simple targets. In case of coronene, a clear signature of plasmon resonance is observed in the analysis of

forward-backward angular asymmetry of low energy electron emission. For fluorene, such signature is not identified probably due to lower oscillator strength of plasmon compared to the

coronene. The theoretical calculation based on the first-order Born approximation with correct boundary conditions (CB1), in general, reproduced the experimental observations qualitatively,

for both the molecules, except in the low energy region for coronene, which again indicates the role of collective excitation. Single differential and total cross sections are also deduced.

An overall comparative study is presented. SIMILAR CONTENT BEING VIEWED BY OTHERS H2 FORMATION VIA NON-BORN-OPPENHEIMER HYDROGEN MIGRATION IN PHOTOIONIZED ETHANE Article Open access 16

August 2023 TIME-RESOLVED RELAXATION AND FRAGMENTATION OF POLYCYCLIC AROMATIC HYDROCARBONS INVESTIGATED IN THE ULTRAFAST XUV-IR REGIME Article Open access 20 October 2021 HYDROGEN MIGRATION

IN INNER-SHELL IONIZED HALOGENATED CYCLIC HYDROCARBONS Article Open access 06 February 2023 INTRODUCTION Understanding of few-body collision dynamics has been a subject of intense research

in past few decades. The first step towards this was the study of fast charge particle impact ionization of simple atoms and molecules. Nowadays, the extent is being extended to the studies

of much more complex molecules of specific interests. For example, biologically relevant complex molecules impacted by energetic ions were investigated extensively from the perspective of

hadron therapy1,2,3,4. The other problem, that has attracted a great deal of attention in recent times, is the understanding of several unidentified astrophysical features in the realm of

microscopic details of the molecules which are present in the interstellar medium (ISM)5. In variety of widely contrasted interstellar (IS) environments a set of ubiquitous, unidentified

infrared bands (UIR) are present in the emission spectra. Besides, the origin of features like diffuse interstellar bands (DIBs) in the absorption spectra in optical/near IR wavelength

range, or the prominent 217.5 nm bump in the interstellar extinction curve are yet to be understood convincingly5,6,7,8. As far as present understanding, the evolution of different

polycyclic aromatic hydrocarbon (PAH) molecules is highly plausible candidate to answer all the open questions regarding these unresolved features5,6,7,8,9,10. PAHs are assembly of benzenoid

rings of _sp_ 2-hybridized C atoms. The peripheral atoms are attached to requisite number of H atoms. The remaining delocalized electrons together form a _π_-electron cloud over the C

skeleton. This gives an extra stability to these molecules to their survival in the harsh IS environment. Generally, PAHs in ISM are formed in the outflows from C-rich giant stars. These can

also be formed from the fragmentation of C dust particles in shocked regions and from photosputtering in diffuse IS clouds. Destruction of larger PAH complex in harsh IS environment is also

an important production procedure for smaller PAHs. This continuous processing of PAHs is believed to be one of the important aspects of the evolution of the ISM, which is certainly related

to the understanding of galaxy formation9,10. For example, the question of heating and cooling of the IS gases automatically came into picture since the first determination of temperature

of the ISM by 21 cm emission/absorption line measurements. In this respect, C allotropes play an important role because these are the main suppliers of free electrons in the IS clouds, thus

contributing to the heating of ISM11. The principal mechanism of the heating process is the removal of electron (ionization) from the allotropes by transferring energy from external

energetic particles (cosmic rays) to the bound electrons. Then the suprathermal electrons produced in this way heat the other IS gases and eventually thermalize the whole system through

elastic collisions. Here the radiative transition plays a minimal role12. Thus, in general, the study of electron emission mechanism of PAH molecules is an important issue which can shed

light on our knowledge of different important astrophysical scenarios. In the IS environment, cosmic ray (CR) is also an important component. It consists of protons, _α_-particles, heavier

ions and electrons of energies spanning from few eV to hundreds of GeV. The sources of these energetic particles are different ISM shocks and supernova ruminants. The lower energy part of

the spectrum, typically upto few hundreds of MeV, cannot be traced directly even with far ranging spacecraft, because these particles are excluded from the heliosphere or severely slowed

down by the solar wind. But it is the most important part of the spectrum, as the intensity distribution sharply falls off with energy, and therefore the high energy (few GeV) cosmic rays

have only marginal effect compared to those of few MeV12. Thus, it is extremely important to understand how the IS components are processed by these energetic ionic species, and this can

only be possible through laboratory studies5. Particularly, it is instructive to study the interaction of MeV energy ions with PAH molecules as it can provide information about how the PAHs

are processed by the low-energy cosmic ray in the ISM, and thus it helps to provide crucial inputs to various astrophysical models13. Other than the astrophysical interest, the researchers

are also quite fascinated about these molecules because of their collective electronic behaviour. It was predicted earlier that these molecules are capable of showing low energy (around 17 

eV) plasmon like collective excitation following some external perturbation14,15,16. Nowadays, this idea has been tried to use in numerous important applications, like to fabricate novel

plasmonic devices with tenability property17. Moreover, in some situations, it directly opens up new possibility of providing answers to some long standing problems in astrophysics like the

origin of 217.5 nm extinction bump18. But fundamentally, unlike C60 19,20,21,22,23 or metals24 or large nucleus25, PAHs are not well explored in the context of collective plasmon resonance.

In this respect the study of electron emission from these molecules can enlighten the issue suitably, as electron emission channel is the fastest mode of de-excitation of these resonances24.

Recently, the signature of such plasmon resonance ((_π_ + _σ_) plasmon resonance around 17 eV) in coronene molecule has been shown in ion collision study26. Earlier, this was indicated in

some of the photo-ionization studies14,15. But the question remains whether such plasmon excitation is also realizable in other PAH molecules or not. Keeping all these in mind, we have

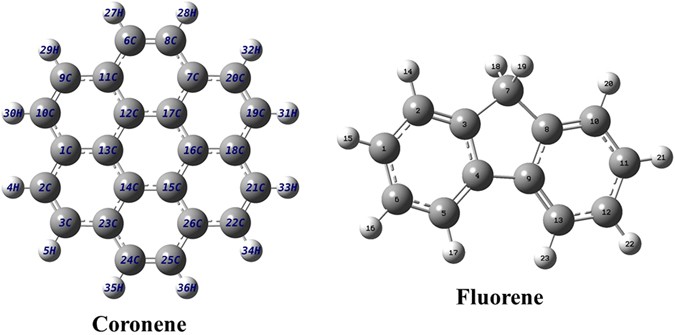
chosen two PAH molecules, namely coronene (C24H12) and fluorene (C13H10), which are different from each other with respect to their size as well as structure, to explore the aspects of

ion-PAH collision. In particular, we intend to investigate the electron emission channels following energetic ion interaction. These are planner molecules of masses of 300 and 166,

respectively. Coronene has seven six membered benzenoid rings, whereas fluorene consists of two six membered benzenoid rings connected by a five member ring (See Fig. 1). The numbers of

valance electron in these are 108 and 62, respectively. For this study we carried out absolute double differential (in electron energy and emission angle) cross section (DDCS)

\((\frac{{d}^{2}\sigma }{d\varepsilon d{\rm{\Omega }}})\) measurements of electron emission from these molecules under the impact of 3.75 MeV/u bare oxygen ions in a wide energy and angular

ranges. It is worth mentioning that, to the best of our knowledge, this is the first detailed electron spectroscopy based measurement of PAHs perturbed by the energetic ions. Apart from

photoionization and photofragmentation studies27,28, the existing literature of ion impact mainly includes post collision recoil-ion based measurements29,30,31,32,33,34,35,36. Other than

that there are some reports available which demonstrate the energy loss mechanism of the energetic ionic projectiles within the PAHs13,36,37,38. In this article, in addition to the

experimental results we also present calculations based on the quantum mechanical approach developed within the first-order Born approximation with correct boundary conditions (CB1). It is

to be mentioned here that the calculations in quantum mechanical approach which requires a complete description of the molecular wavefunctions in term of the linear combinations of atomic

orbitals (LCAO), give much more realistic description of the complex collision mechanism, but on the other hand, are very hard to perform. Such a comparison with _ab initio_ model

calculation is presented here for the first time to understand overall ion-PAH collision dynamics, it was not available in the earlier work on ion collision with coronene26, which mainly

focused on the plasmon excitation aspects. It may also be mentioned that the electron DDCS measurements provide more stringent test to the theoretical models compared to single differential

or total cross section measurements. Moreover, for comparison purpose, we also provide the results of similar measurements for smaller atomic and molecular systems with the same projectile

specifications. This particularly helps us to discuss about the effects of the collective mode of the PAH molecules on the electron emission spectrum. RESULTS ELECTRON DDCS: ENERGY

DISTRIBUTION In Fig. 2, the energy distributions of the absolute DDCS at six representative emission angles are shown for coronene. The data for Ne and CH4 targets are also displayed at some

of the plots along with the coronene data for comparison. The solid line in each plot represents the CB1 calculation for the coronene target. Apart from the fact that the cross sections for

the Ne and the CH4 are always smaller than that of the coronene, in general, the qualitative behaviour of the distributions are observed to be very similar to each other, i.e. a rapid

decrease in cross section with increasing electron energy. The low energy part of the spectrum, namely the soft collision region, is caused by the large impact parameter collisions involving

low momentum transfer. In each of these plots, the broad peak around 240 eV corresponds to _K_-_LL_ Auger electron emission from C atoms. The clearer visibility of the peak in the backward

angles compared to the forward and the intermediate angles is due to the fact that the cross section corresponding to the Coulomb ionization continuum is less at backward angles compared to

the other angle, whereas the _K_-_LL_ Auger cross section distribution is almost isotropic in nature. This is very similar to the ion-atom collision cases39. Now as far as comparison with

the CB1 calculation is concerned, it underestimates the experimental data for most of the electron energy regions at all angles. The factor (m) by which it underestimates decreases from

about 3.0 to 1.1 with increasing value of emission angle. But, qualitatively it reproduces the features of the observed distributions quite well except only the _K_-_LL_ Auger peak part

which, being a characteristic relaxation process, is out of the scope of this model calculation. A further closer look into the plots reveals that the slopes of the theoretically predicted

distributions, especially after around 20 eV, are little steeper than that of the observed distributions for all angles. In Fig. 3, similar DDCS energy distributions are shown for fluorene.

In this case the qualitative features of the distributions are very similar to that of the above case. If we compare the absolute values of cross section between coronene and fluorene, it is

always a factor of about 2.0 less for the later compared to the former. This can be qualitatively understood from the sizes of the molecules or numbers of valance electron. Regarding the

comparison with the theory, the CB1 predicted curve is slightly different than the previous case in terms of overall characteristics. It shows a flat behaviour or slightly increasing trend

at some angles upto around 8 eV. This does not match with the experimental observation of smoothly decreasing trend, and also this does not match with our expectation. After that it exhibits

usual decreasing trend with the energy. In absolute scale, it underestimates the cross section by a factor (m) of 1.2 to 1.5, which was also the case for coronene. The overall comparison

with the theory would be more clear from Fig. 4, where the ratio of experimental and theoretical DDCS values are plotted as a function of electron energy for both coronene and fluorene. For

coronene, the deviation is minimum in the 20–30 eV region for all angles. At intermediate and backward angles, in this region the theory slightly overestimates the experimental data, whereas

in the rest of the region it underestimates the data. After that specified region the deviation increases with electron energy. In general, at intermediate and backward angles the agreement

between the theory and the experiment is better than that at the forward angle. In case of fluorene, the overall discrepancy is less compared to the case of coronene. Here the agreement is

best at around 8 eV, and at the intermediate angle compared to the other angles. At extreme angles the deviation increases with electron energy. ELECTRON DDCS: ANGULAR DISTRIBUTION The

angular distributions of absolute DDCS for coronene are presented in Fig. 5 for eight representative electron energies. The distributions for CH4, scaled by a factor n, are plotted together

for comparison. The CB1 calculation, which had to be also scaled by a factor m, is represented by the solid line. At lower energies upto around 20 eV, the distributions for coronene are

steeply falling with increasing emission angle. This is in sharp contrast to the distribution observed for CH4. It is almost flat for 3 eV and 7 eV. After that a hump like structure at the

intermediate angles due to binary nature collision arises. This behaviour is very similar to the ion-atom collision case39,40. The main striking difference between these two distributions is

the associated forward-backward angular asymmetry, i.e. the relative difference between the cross sections corresponding to the forward and the backward angles. For example, at 7 eV, for

coronene, the forward angle DDCS is about 3.2 times higher than the backward angle DDCS, whereas this value is only 1.2 for CH4. As electron energy increases, the amount of contrast comes

down. At higher energies, the angular distributions for coronene are very similar to that of the CH4. In both the cases the peak at the intermediate angles corresponding to the binary

encounter collision becomes prominent. The forward-backward angular asymmetries are also observed to be very similar for both the cases. It is quite large compared to that for lower

energies. This large degree of angular asymmetry in the higher energy region is well understood in terms of projectile post collision effect39,40. As discussed earlier, the CB1 calculation

underestimates the data almost for all energy ranges. In the low energy part of the spectrum, it also fails to reproduce the qualitative features of the observed angular distribution. It

predicts an angular distribution which is expected from the binary nature of collision. The calculated forward-backward angular asymmetry is also very negligible compared to the observed

one. As the value of the electron energy increases, the agreement becomes much better. After about 100 eV, it reproduces the qualitative features of the observed angular distributions well,

especially at the intermediate angular region. This region is dominated by the binary encounter process, i.e. purely a two-body collision process. As a result it is well expected that the

calculation based on quantum mechanical first-order approximation like CB1 would give better results. But at extreme angles the agreement is relatively worse. Mainly it fails to reproduce

the observed forward-backward angular asymmetry. It predicts much smaller forward-backward angular asymmetry compared to the observed one. In Fig. 6, similar angular distributions of DDCS

are shown for fluorene along with the distributions given by the theory and the CH4. At low energies, the nature of the distributions is different in several aspects from the case of

coronene. In this case it is much more flatter distribution compared to coronene and very much similar to the case of CH4. Naturally, the associated forward-backward angular asymmetry is

much lower. After 13 eV, it is even less than that for CH4 and it starts exhibiting the features of binary nature of collision, i.e. the hump like structure at the intermediate angles.

Overall, qualitatively, the distributions for all energies are very similar to the cases of CH4. Though there are qualitative differences between low energy distributions of coronene and

fluorene, the angular distributions corresponding to the higher energy electrons are quite similar to each other, mainly manifesting the features related to binary nature of collision and

large forward-backward angular asymmetry. In this case the qualitative agreement with the distributions predicted by CB1 calculation is much better compared to the case of coronene. Here the

low energy distributions are also quite well reproduced by the theory, relative to the earlier case. The main limitation is observed in the discussion of forward-backward angular asymmetry.

Here also the calculation predicts much less forward-backward angular asymmetry compared to the observed one. Other than that, a good agreement is seen at most of the angular regions,

especially at the intermediated angular region. FORWARD-BACKWARD ANGULAR ASYMMETRY As seen in the above section, the forward-backward angular asymmetry is an important aspect of the electron

angular distribution, which differs with target to target. Detailed analysis of it can give crucial information about the underlying mechanism of electron emission. To have a quantitative

understanding of this, in Fig. 7(a,b), we have plotted the energy distributions of DDCS ratio signifying the enhancement of cross section at forward angle relative to backward angle, for

coronene and fluorene, respectively. The angle 30° is chosen as forward angle and as backward angle 140° and 150° are chosen for coronene and fluorene targets, respectively. Similar

distributions for other simpler targets, i.e. Ne and CH4, are also plotted in the same plots for comparison. If we first look at the distributions of Ne and CH4, these are qualitatively very

similar to each other. In general, the ratio value increases monotonically from very low value to the higher value. The low value for the low energy electrons is due to nearly isotropic

angular distribution, which is caused by the target centre effect. As these electrons are emitted in large impact parameter collisions, their distributions would be mainly governed by the

effective Coulomb field of the residual target ion. On the other hand, the monotonically increasing behaviour is generally attributed to the projectile post collision effect. Because of the

post collision projectile Coulomb field, the ionized electrons are dragged in the forward direction by the highly charged ionic projectile, which in turn increases the cross section in the

forward direction compared to the backward direction. These higher energy electrons essentially move in a region of combined Coulomb fields of both the projectile ion and the residual target

ion. This influence increases with increasing electron energy, because compared to the low energy electrons the velocities of the higher energy electrons are closer to the velocity of the

projectile ion. As a result these are more influenced by the projectile Coulomb filed compared to the others39,40. Now, if we look back to the distribution for coronene (Fig. 7(a)), we

realize that the nature of the distribution is quite different than that of the above mentioned targets. In this case, it starts from a slightly higher ratio value and then forms a broad

peak like structure at around 10 eV. Then 30 eV onwards it again follows an increasing trend and matches with the distributions corresponding to Ne and CH4 targets. Thus, though the

projectile post collision effect picture, which generally works very well for the simpler targets, seems to be adequate to explain the behaviour in the higher energy region, the peak

structure in the low energy region can not be explained by this and the target centre emission picture. It can be explained taking into account of collective plasmon excitation. For this

molecule the predicted (_π_ + _σ_) plasmon resonance energy is around 17 eV16. Therefore, we can see the signature of plasmon resonance in the emitted electron spectra at around \(\hslash

{\omega }_{plasmon}-{I}_{p}\sim 10\,{\rm{eV}}\), since the ionization potential (_I_ _p_ ) is 7.29 eV (1_st_) for coronene (in gas phase). The observed peak position, here, very closely

matches with this expected position of the plasmon electron signature16,26. In the inset of the figure it can be seen to match with the exact plasmon excitation energy, i. e. 17 eV.

According to ref.26, this plasmon signature is visible in terms of angular asymmetry of electron distribution because of the oscillatory nature of plasmon resonance, which is perturbed by

strong perturbing field of ionic projectile. This has been shown through a photo electron angular distribution model, which is calculated for large perturbation strength of the ionizing

system41,42,43. In case of fluorene, the qualitative features of the distribution are quite different from that of the coronene, especially in the low energy region, but very much similar to

the simpler targets. It shows a monotonically increasing behaviour with increasing electron energy, though it takes the lowest value after about 40 eV among all the studied targets. Overall

there is no noticeable feature in the distribution, which is quite different from the behaviour shown by the simpler targets or from our present understanding. More specifically the plasmon

peak, similar to the case of coronene, in the low energy region is not visible here. Quantitatively, fluorene shows lesser asymmetry compared to that of coronene throughout the entire

energy range. Now, in these cases the distributions predicted by CB1 calculation are indicated by solid lines. For coronene, in general, it fails to reproduce the observed asymmetry. It

predicts much lower value of the ratio than the observed one throughout the entire energy scale. It also does not predict any peak structure in the low energy region. The failure of

reproducing the plasmon peak can be justified because this calculation does not incorporate any plasmon kind of collective excitation. For fluorene also, the CB1 calculation fails to

reproduce the observed distribution well. It suggests lower value asymmetry than the observed one for most of the energy region. At extreme low energy region it shows a increasing trend with

decreasing energy, which is not expected normally. In general, the underestimation of the asymmetry in both the cases, especially in the higher energy region, may be because of the fact

that it is not a two centre distorted wave theory. In the distorted wave theories the effect of projectile Coulomb field before and after the collision is suitably incorporated, because of

which the results are expected to be relatively better39,40. But this kind of calculation for these complex collision systems is hard to perform. COMPARISON BETWEEN CORONENE AND FLUORENE In

Fig. 8(a–c), DDCS ratios corresponding to coronene and fluorene are shown for different angles. In forward and intermediate angles, in general, the ratio value increases with electron

energy. This value reaches to a value as large as about 5.0 at round 200 eV. On the other hand at backward angle, it does not show increasing trend. After showing slightly increasing

behaviour upto around 25 eV, it saturates at the value around 1.8, with slight fluctuation around it. It should be mentioned here that the number of valence electrons in coronene is 1.74

times more than that for fluorene. This is indicated by the dashed horizontal line in the plots. At the backward angle the DDCS ratio follows this line very well for most of the energy

region. But the cross section ratios at forward and intermediate angles do not show similar scaling behaviour. The reason behind this is not fully understood. At the forward angle, in

addition to the increasing trend, the peak structure corresponding to the plasmon excitation in coronene is prominently visible. This is clearly shown in the inset (d). The peak position

very well matches with the expected plasmon energy i. e. 17 eV, as has been shown in the forward-backward ratio (in previous figure and ref.26). Additionally we also take the similar ratio

with CH4 data, instead of fluorene. This is plotted in other inset (e), which also confirms the observation of plasmon peak at 17 eV. The contrbution of plasmon excitation is quite strong in

case of forward electron emission and almost negligible for backward angle, as shown in ref.26. The observed nearly flat behaviour of the ratio around 1.74 [in Fig. 8(c)] for backward angle

is consistent with this picture i.e. negiligible plasmon contribution. The sharp increase in the ratio values at higher electron energies in case of forward angles can not be explained at

this stage. SINGLE DIFFERENTIAL CROSS SECTION (SDCS) AND TOTAL CROSS SECTION (TCS) To understand the overall angular and energy distributions of the emitted electrons, the SDCSs have been

derived by integrating the DDCS spectra. In Fig. 9 its energy and angular distributions are displayed. For both the targets, the overall qualitative features of the energy distributions are

very similar to that of the DDCS distributions, and these are very similar to each other also. Here the C K-LL Auger peaks are clearly visible. Though the gross trends of the distributions

for both the targets are well reproduced by the CB1 calculation except the Auger part, quantitatively it underestimates the experimental data through out the entire energy region. In

contrast to the energy distribution, the angular distributions of SDCS corresponding to these targets are quite different from each other. For coronene, the forward angle cross sections are

seen to be much higher compared to the backward angle cross sections. The usual feature of binary encounter peak is almost absent. It suggest that the low energy features in the DDCS level

mainly govern the overall angular distribution. On the other hand, for fluorene, it is like ion-atom collision behaviour. There is forward-backward angular asymmetry present, but the binary

encounter peak is prominently visible. The amount of forward-backward angular asymmetry is also much less compared to that of coronene. At the extreme backward angles, the cross sections for

these targets are almost same with each other. The prediction of the CB1 calculation, for coronene, does not match with the observation. Apart from the fact that it underestimates the cross

sections as mentioned earlier, it provides a distribution which is very similar to the cases of the atomic targets39,40. It presents a prominent binary encounter peak at the intermediate

angular region and the forward-backward angular asymmetry is much smaller than the observed one. For fluorene, besides the fact that it underestimates the experimental data, qualitatively it

reproduces the angular distribution relatively well. There are some discrepancies mainly for the estimation of forward-backward angular asymmetry. It predicts more symmetric distribution

than the observed one. The TCS obtained from the experimental data for coronene and fluorene are about 56.729 Gb and 26.642 Gb, respectively, whereas these values estimated by the CB1

calculation are about 38.243 Gb and 20.703 Gb, respectively. Evidently, the theoretical calculation underestimates the experimental TCS for coronene by factor a of about 1.5 and it is about

1.3 for fluorene. DISCUSSION To summarize, we have measured the energy and the angular distributions of absolute DDCS of electron emission from coronene and fluorene molecules, which are two

of the important members of the PAH family, under the collision of 3.75 MeV/u O8+ projectiles. The energy distributions of DDCS for both the targets are seen to be similar and these match

with the general trend of the ion-atom or simpler molecule collision. On the other hand, there are some differences in the angular distributions corresponding to these PAH molecules,

particularly in the low energy region. The distributions for fluorene shows isotropic behaviour at low energies. At higher energies it shows the expected behaviour, which can be explained by

the binary encounter collision picture and two centre effect. These behaviours are nearly similar to that of the simpler targets. In contrary, the low energy electron distribution for

coronene shows an unusually large forward-backward angular asymmetry which is due to the plasmon excitation, as shown also earlier. On the other hand, in the higher energy region, the

characteristics of electron emission distributions are similar to the cases of ion-atom or small molecule collision. The signature of plasmon resonance for the case of coronene is clearly

visible as a peak structure in the energy distribution of forward-backward DDCS ratio, whereas, for fluorene, the DDCS ratio distribution does not show such prominent peak in the plasmon

energy region. The non-visibility of such peak in case of the fluorene molecule can be due to the low oscillator strength of plasmon resonance. In comparison with the coronene, it has much

less number of available electron to form a polarized electron cloud which can oscillate against the ionic cage and produces plasmon resonance. Therefore, the strength of the plasmon

resonance in PAH molecules certainly scales with the size of the molecule or number of available electron that can participate in plasmon oscillation. The case of such resonance in C60 23

also fits with this argument. We have also studied the ratio of DDCS of the two molecules which also indicates the presence of a peak exactly at the plasmon excitation energy. This is

consistent with our earlier observation of the plasmon contribution as derived from the forward-backward DDCS ratio. This conclusion is also strenghened from the observed peak in the ratio

obtained using coronene and CH4 targets. In order to understandstand the general behaviour of the energy and angular distributions of the DDCS data we have compared these with quantum

mechanical calculation developed within the first-order Born approximation with correct boundary conditions (CB1). However this model does not take into account the many-body correlations or

plasmon excitation. For both the targets, qualitatively, except in the KLL-Auger-energy region, the energy distributions of the DDCS are well reproduced by this. Quantitatively, it

underestimates the experimental data by a factor of about 1.1 to 3.0 and 1.2 to 1.5 for coronene and fluorene, respectively. All the features of the angular distributions of DDCS for

fluorene are also reproduced well by the calculations. But in case of coronene, though there is a good qualitative agreement with the higher energy data, it fails to reproduce the

experimentally observed behaviour in the low energy region. Mainly it is unable to reproduce the observed large asymmetry in the angular distributions. There is a need to have a model which

can include the collective behaviour in such large molecules and the projectile post collision effect to explain the experimental observations. These studies, particularly the collective

excitation or many body effects may also be referred to the study of ion collisions with large molecules, such as, the DNA-bases, fullerenes etc, besides the other members of the PAH family.

Apart from these the overall understanding of the energy and angular distributions of the absolute DDCS, SDCS and the derived TCS of the electron emission in ion-PAH collision, that come

out from this study, would be beneficial in terms of crucial input to different astrophysical models. METHODS OVERVIEW OF THE EXPERIMENTAL PROCEDURE In the present experiment, electron DDCS

measurements for coronene and fluorene molecules were carried out with 3.75 MeV/u O8+ ions. The use of bare highly charged ions ensures to work in a strong perturbation regime as well as get

rid of other complicated interactions44,45. The effusive vapour jets of coronene and fluorene molecules (99% pure, Sigma-Aldrich) were prepared by heating these at around 200 °C and 50 °C,

respectively. For coronene experiment, a heater assembly, consisting of an electrically controlled oven with a nozzle of aspect ratio 10 on top, whose position can be controlled by an XYZ

manipulator, was placed within a high vacuum scattering chamber, whose base pressure was maintained better than 2 × 10−7 Torr. To shield the electron detector from thermal radiation, a water

cooling jacket was put around the oven. For fluorene experiment, the molecular holder was kept out side the chamber. A metal tube was used to connect the nozzle with the holder. In this

case it was possible like that because of higher vapour pressure. These experiments demand uniform flow of target molecules throughout the experiment. To ensure this, initially the oven

temperature was raised very slowly and after achieving desired vapour density, the temperature was kept fixed. The _in situ_ characterization of the target flow was done using a quartz

crystal thickness monitor mounted on the top of the interaction region. It shows the thickness of the deposited layer of target molecule with time. From that the variation of deposition rate

was calculate and it was observed to vary by about 8% over a period of about 16 hours, for both the molecules. The projectile ion beam, extracted from the BARC-TIFR 14 MV tandem Pelletron

accelerator facility in Mumbai, India, was made incident on the target effusive jet. Special cares were taken to get rid of stray electric field and earth’s magnetic field which affect the

low energy electron detection. The number of projectile ions was determined by detecting them by a Faraday cup. The emitted electrons were energy analysed by a hemispherical electrostatic

analyser whose energy resolution is around 6%46, and these were detected by a channel electron multiplier. By rotating the spectrometer the angular distribution was determined. In the

present experiments the electrons were detected in the energy range of 1 to 320 eV, and the spectra were taken at different angles between 30° and 150°. To get the information about the

background, same measurements were done without effusive jet. From the measured electron count and by background subtraction the DDCSs were obtained from the first principle46. To obtain the

absolute value of the cross section, the exact determination of the number of target molecules at the interaction region is necessary. But in this kind of effusive jet experiment, it is

difficult to get this number reliably. Without this the relative DDCSs can be determined from the electron counts and employing solid angle path length correction for jet geometry properly.

To avoid this problem as well to raise the relative DDCS values to the absolute scale, we used a novel method. In another flooded chamber experiment, with the same projectile, we determined

absolute total C _K_-_LL_ Auger cross section (_σ_ _Abs_ (_C_ − _KLL_, _CH_ 4)) for methane target by integrating the DDCS data twice in the Auger region. Similarly, the relative Auger cross

sections (_σ_ _Rel_ (_C_ − _KLL_, _PAH_)) for PAH targets were also determined from the relative DDCSs. In all the cases exponential baseline subtraction was done in the single differential

cross section (SDCS) (d_σ_/d_ε_) level after performing proper fitting. Now, since Auger electron emission is an inner-shell ionization process, we assumed that the C _K_-_LL_ Auger

emission cross section is the same for CH4 and PAH targets, scaled by the number of C atoms. From that equality condition we got the unknown normalization factor as, $$N=\frac{{\sigma

}_{Abs}(C-KLL,C{H}_{4})\times {n}_{C}}{{\sigma }_{Rel}(C-KLL,PAH)}$$ (1) where _n_ _C_ is the number of C atoms of the PAH molecules. As the continuum part of the DDCS spectra as well as the

Auger peak were produced from same target density, jet profile, beam overlap and other unknown experimental parameters, we could use the same absolute normalization factor as well to raise

the continuum part to the absolute scale. $$Absolute\,DDCS\,for\,PAH=N\times Relative\,DDCS\,for\,PAH$$ (2) Further details of the normalization procedure is available in ref.2. The overall

uncertainty in these absolute cross section measurements were estimated to be about 10% to 15% which mainly arises from the target density fluctuation, normalization procedure and the

statistical uncertainty. THEORETICAL MODEL: CB1 The cross sections presented in this work have been calculated within the first-order Born approximation with initial and final wave functions

verifying correct boundary conditions. This approach, successfully used earlier by Champion _et al_.47 for investigating ionization of water48,49,50, can be interpreted as an extension of

the CB1 model introduced by Belkić _et al_.51 for studying the electron capture from atomic targets. In the laboratory frame, the triply differential cross sections (TDCS), namely,

differential in the scattering direction (Ω _s_ ), differential in the ejection direction (Ω _e_ ) and differential in the ejected energy (_E_ _e_ ), can be simply written as $${\sigma

}^{(3)}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e})\equiv \frac{{d}^{3}\sigma }{d{{\rm{\Omega }}}_{s}d{{\rm{\Omega }}}_{e}d{E}_{e}}=\sum _{j=1}^{N}\,\frac{{d}^{3}{\sigma

}_{j}}{d{{\rm{\Omega }}}_{s}d{{\rm{\Omega }}}_{e}d{E}_{e}}\equiv \sum _{j=1}^{N}\,{\sigma }_{j}^{\mathrm{(3)}}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e}),$$ (3) where _N_ refers to

the number of molecular orbitals used in the target description (_N_ = 44 and 78 for fluorene and coronene, respectively). The current target description is based on the restricted

Harthree-Fock method with geometry optimization (RHF/3-21G)52 and models each molecular subshell of the targets by means of linear combinations of atomic orbitals provided within a complete

neglected differential overlap (CNDO) approach. In these conditions, the TDCS for each molecular orbital labeled _j_ can be expressed as a weighted sum of atomic triply differential cross

sections \({\sigma }_{at,i}^{\mathrm{(3)}}\) corresponding to the different atomic components involved in the molecular subshell description, namely, $${\sigma

}_{j}^{\mathrm{(3)}}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e})=\sum _{i}\,{\xi }_{j,i}\cdot {\sigma }_{at,i}^{\mathrm{(3)}}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e}),$$ (4)

where _ξ_ _j_,_i_ stand for the _effective_ number of electrons of the different atomic orbitals and where the atomic triply differential cross \({\sigma }_{at,i}^{\mathrm{(3)}}\) are

calculated by using the well-known expression, namely, $${\sigma }_{at,i}^{\mathrm{(3)}}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e})={\mathrm{(2}\pi )}^{4}\cdot {\mu }^{2}\cdot

\frac{{k}_{s}{k}_{e}}{{k}_{i}}\cdot {|{[{T}_{a,b}]}_{i}|}^{2}$$ (5) In Eq. 5, [_T_ _a_,_b_ ] _i_ denotes the atomic transition matrix element between an initial state _a_ and a final state

_b_ with _μ_ = _A_ _ion_  · _M_ _p_ where _A_ _ion_ designates the projectile mass number and _M_ _p_ the proton mass whereas K _i_ , K _s_ , and K _e_ represent the wave vectors of the

incident ion, the scattered ion and the ejected electron, respectively. Furthermore let us note that the collisional process is here described within the independent electron model (IEM) and

employing frozen core approximation. These approximations have been successfully used for numerous ionization reactions (see for example refs53,54). It was shown that, the interaction

between the projectile and the residual target plays a negligible role when doubly differential cross sections (DDCS) are determined as a function of the linear momentum of the emitted

electron55,56,57. Now the DDCSs can be easily obtained after integration of the TDCS over the projectile scattering direction Ω _s_ with a transition matrix element

\({[{\tilde{T}}_{a,b}]}_{i}\), namely, $${[{\tilde{T}}_{a,b}]}_{i}=\langle {\phi }_{i,b}(R)\cdot {\varphi }_{i,b}(r)|\frac{{Z}_{P}}{R}-\frac{{Z}_{P}}{|R-r|}|{\phi }_{i,a}(R)\cdot {\varphi

}_{i,a}(r)\rangle ,$$ (6) where R and R give the positions of the projectile and of the active electron, respectively and _ϕ_ _i_,_a_ (_R_) and _ϕ_ _i_,_b_ (_R_) refer to incoming and

outgoing projectile plane waves, whereas _φ_ _i_,_b_ (_r_) stands for the ejected-electron Coulomb wave function, respectively. _φ_ _i_,_a_ (_r_) represents the atomic wave function of the

_i_ _th_-orbital used in the CNDO expansion of each target molecular subshell. These atomic wave functions refer to the C(_2p_) and H(_1_  _s_) ones and are expanded on spherical harmonic

basis with a radial part given in terms of Slater functions, namely, $${\mathrm{\varphi ;}}_{i,a}(r)=\sum _{k=1}^{{N}_{i}}\,\frac{{\mathrm{(2}{\varsigma

}_{k})}^{{n}_{ik}+\mathrm{1/2}}}{\sqrt{\mathrm{(2}{n}_{ik})!}}\cdot {r}^{{n}_{ik}-1}\cdot {e}^{-{\varsigma }_{ik}\cdot r}\cdot {Y}_{{l}_{ik}{m}_{ik}}({{\rm{\Omega }}}_{r})\equiv \sum

_{k=1}^{{N}_{i}}\,{f}_{ik}(r)\cdot {Y}_{{l}_{ik}{m}_{ik}}({{\rm{\Omega }}}_{r}),$$ (7) where _N_ _i_ denotes the number of partial waves (_n_ _ik_ , _l_ _ik_ , _m_ _ik_ ) used for the

description of the _i_ _th_ atomic orbital. For more details about these coefficients, we refer the reader to the Clementi’s tables of atomic functions58. Finally, it should be here

mentioned that the \(\frac{{Z}_{p}}{R}\) term in the perturbative potential of Eq. 6 corrects the Coulomb long range behavior of the interaction between the projectile and the active

electron at their asymptotic separations. Thus, by using the well-known partial-wave expansion of the plane wave as well as that of the Coulomb wave, we easily access to an analytical form

of the TDCS which may be, as previously mentioned, converted into DDCS by means of a numerical integration over the projectile scattering direction, namely, $$\begin{array}{rcl}{\sigma

}_{at,i}^{\mathrm{(2)}}({{\rm{\Omega }}}_{e},{E}_{e}) & \equiv & \int d{{\rm{\Omega }}}_{s}\cdot {\sigma }_{at,i}^{\mathrm{(3)}}({{\rm{\Omega }}}_{s},{{\rm{\Omega }}}_{e},{E}_{e})\\

& = & \frac{32{k}_{s}}{{k}_{i}{k}_{e}{q}^{4}}\int d{{\rm{\Omega }}}_{s}\cdot \sum _{k=1}^{{N}_{i}}\,[{(\frac{{X}_{ik}^{^{\prime} }}{4\pi })}^{2}+\sum _{\mu

=-{l}_{ik}}^{{l}_{ik}}\,[|{Z}_{ik}{|}^{2}\\ & & -\,\Re e(\frac{{Z}_{ik}}{\sqrt{\pi {\hat{l}}_{ik}}}{Y}_{{l}_{ik}\mu }^{\ast }\,({{\rm{\Omega }}}_{e})\,{i}^{{l}_{ik}}{e}^{-i{\sigma

}_{{l}_{ik}}}{X}_{ik}^{^{\prime} })]]\end{array}$$ (8) where _σ_ _l_ denotes the Coulomb phase shift and \(\Re e(z)\) the real part of the complex _z_, whereas

$$\begin{array}{rcl}{X}_{ik}^{^{\prime} }\equiv {X}_{ik}^{^{\prime} }({k}_{e}) & = & {\int }_{0}^{\infty }dr\cdot r\cdot {F}_{{l}_{ik}}({k}_{e},r)\cdot {f}_{ik}(r)\\ {Z}_{ik}\equiv

{Z}_{ik}({k}_{e},q) & = & \sum _{l=0}^{\infty }\,\sum _{{l}_{1}=|l-{l}_{ik}|}^{l+{l}_{ik}}\,\sum _{{m}_{1}=-{l}_{1}}^{{l}_{1}}\,{i}^{l-{l}_{1}}\cdot {e}^{i{\sigma }_{{l}_{1}}}\cdot

{X}_{ik}^{l{l}_{1}}\cdot {Y}_{{l}_{1}{m}_{1}}({{\rm{\Omega }}}_{e})\\ & & \cdot \,{Y}_{l{m}_{1}-\mu }^{\ast }({{\rm{\Omega }}}_{q})\cdot {(-\mathrm{1)}}^{{m}_{1}}\cdot

\sqrt{{\hat{l}}_{1}\hat{l}}\cdot (\begin{array}{l}{l}_{1}\,l\,{l}_{ik}\\ 0\,0\,0\end{array})\cdot (\begin{array}{l}{l}_{1}\,\quad \,\,\,\,l\,\quad {l}_{ik}\\ -{m}_{1}\,{m}_{1}-\mu \,\,\mu

\end{array}).\end{array}$$ (9) with \(\hat{l}=2l+1\) and where _q_ = _k_ _i_  − _k_ _s_ denotes the momentum transfer. Note that in Eq. 9, _F_ _l_ (_k_ _e_ , _r_) refers to the radial

hypergeometric function whereas \({X}_{ik}^{l{l}_{1}}({k}_{1},q)\) is expressed as $${X}_{ik}^{l{l}_{1}}({k}_{1},q)={\int }_{\,0}^{\,\infty }\,dr\cdot r\cdot {F}_{{l}_{1}}({k}_{1},r)\cdot

{j}_{l}(qr)\cdot {f}_{ik}(r),$$ (10) where _j_ _l_ (_qr_) refers to the Bessel function. Finally, note that in the present quantum mechanical calculations, the effective target charge seen

by the escaping ejected electron is not equal to the asymptotic charge, namely, \({Z}_{T}^{\ast }=1\) but taken as \({Z}_{T}^{\ast }=\sqrt{-2{n}_{\alpha }^{2}{\varepsilon }_{\alpha }}\)

where _n_ _α_ refers to the principal quantum number of each atomic orbital component used in each MO expansion whereas the active electron orbital energy _ε_ _α_ is related to the

ionization energies _B_ _j_ (>0) of the occupied molecular orbitals by _ε_ _α_  = −_B_ _j_ . CHANGE HISTORY * _ 04 DECEMBER 2017 A correction to this article has been published and is

linked from the HTML version of this paper. The error has been fixed in the paper. _ REFERENCES * Moretto-Capelle, P. & Le Padellec, A. Electron spectroscopy in proton collisions with

dry gas-phase uracil base. _Physical Review A_ 74, 062705, doi:10.1103/PhysRevA.74.062705 (2006). Article  ADS  Google Scholar  * Agnihotri, A. N. _et al_. Doubly differential distribution

of electron emission in ionization of uracil in collisions with 3.5-MeV/u bare C ions. _Physical Review A_ 87, 032716, doi:10.1103/PhysRevA.87.032716 (2013). Article  ADS  Google Scholar  *

Nandi, S. _et al_. Double-differential cross sections for ionization of H2O by fast bare O ions: Comparison with continuum-distorted-wave eikonal-initial-state calculations in prior and post

forms. _Physical Review A_ 87, 052710, doi:10.1103/PhysRevA.87.052710 (2013). Article  ADS  Google Scholar  * de Vera, P., Garcia-Molina, R. & Abril, I. Angular and Energy Distributions

of Electrons Produced in Arbitrary Biomaterials by Proton Impact. _Physical Review Letters_ 114, 018101, doi:10.1103/PhysRevLett.114.018101 (2015). Article  ADS  PubMed  Google Scholar  *

Tielens, A. G. G. M. The molecular universe. _Reviews of Modern Physics_ 85, 1021–1081, doi:10.1103/RevModPhys.85.1021 (2013). Article  ADS  CAS  Google Scholar  * Leger, A. &

D’Hendecourt, L. Are polycyclic aromatic hydrocarbons the carriers of the diffuse interstellar bands in the visible? _Astronomy and Astrophysics_ 146, 81–85 (1985). ADS  CAS  Google Scholar

  * Allamandola, L. J., Hudgins, D. M. & Sandford, S. A. Modeling the Unidentified Infrared Emission with Combinations of Polycyclic Aromatic Hydrocarbons. _The Astrophysical Journal_

511, L115–L119, doi:10.1086/311843 (1999). Article  ADS  CAS  PubMed  Google Scholar  * Xiang, F. Y., Li, A. & Zhong, J. X. A Tale of Two Mysteries in Interstellar Astrophysics: The 2175

Å Extinction Bump and Diffuse Interstellar Bands. _The Astrophysical Journal_ 733, 91, doi:10.1088/0004-637X/733/2/91 (2011). Article  ADS  Google Scholar  * Bakes, E. L. O. & Tielens,

A. G. G. M. The photoelectric heating mechanism for very small graphitic grains and polycyclic aromatic hydrocarbons. _The Astrophysical Journal_ 427, 822–838, doi:10.1086/174188 (1994).

Article  ADS  CAS  Google Scholar  * Bakes, E. L. O. & Tielens, A. G. G. M. The Effects of Polycyclic Aromatic Hydrocarbons on the Chemistry of Photodissociation Regions. _The

Astrophysical Journal_ 499, 258–266, doi:10.1086/305625 (1998). Article  ADS  CAS  Google Scholar  * Henning, T. & Salama, F. Carbon in the Universe. _Science_ 282, 2204,

doi:10.1126/science.282.5397.2204 (1998). Article  ADS  CAS  PubMed  Google Scholar  * Lequeux, J. The Interstellar Medium. _Springer_-_Verlag Berlin Heidelberg_ (2005). * Micelotta, E. R.,

Jones, A. P. & Tielens, A. G. G. M. Polycyclic aromatic hydrocarbon processing by cosmic rays. _Astronomy and Astrophysics_ 526, A52, doi:10.1051/0004-6361/201015741 (2011). Article  ADS

  Google Scholar  * Ling, Y. & Lifshitz, C. Plasmon excitation in polycyclic aromatic hydrocarbons studied by photoionization. _Chemical Physics Letters_ 257, 587–591,

doi:10.1016/0009-2614(96)00592-1 (1996). Article  ADS  CAS  Google Scholar  * Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S. & Leach, S. VUV peaks in absorption spectra and

photoion yield curves of polycyclic aromatic hydrocarbons and related compounds. _International Journal of Mass Spectrometry and Ion Processes_ 167, 35–53 (1997). Article  ADS  Google

Scholar  * Verkhovtsev, A. V., Korol, A. V. & Solov’yov, A. V. Quantum and classical phenomena in photoionization of carbon nanostructures. _Journal of Physics: Conference Series_ 490,

012159, doi:10.1088/1742-6596/490/1/012159 (2014). Google Scholar  * Manjavacas, A. _et al_. Tunable Molecular Plasmons in Polycyclic Aromatic Hydrocarbons. _ACS Nano_ 7, 3635–3643,

doi:10.1021/nn4006297 (2013). * Duley, W. W. A Plasmon Resonance in Dehydrogenated Coronene (C24H _x_ ) and Its Cations and the Origin of the Interstellar Extinction Band at 217.5

Nanometers. _The Astrophysical Journall_ 639, L59–L62, doi:10.1086/502649 (2006). Article  ADS  CAS  Google Scholar  * Bertsch, G. F., Bulgac, A., Tomanek, D. & Wang, Y. Collective

plasmon excitations in C60 clusters. _Physical Review Letters_ 67, 2690–2693, doi:10.1103/PhysRevLett.67.2690 (1991). Article  ADS  CAS  PubMed  Google Scholar  * Kadhane, U., Misra, D.,

Singh, Y. P. & Tribedi, L. C. Effect of Collective Response on Electron Capture and Excitation in Collisions of Highly Charged Ions with Fullerenes. _Physical Review Letters_ 90, 093401,

doi:10.1103/PhysRevLett.90.093401 (2003). Article  ADS  CAS  PubMed  Google Scholar  * Scully, S. W. _et al_. Photoexcitation of a Volume Plasmon in C60 Ions. _Physical Review Letters_ 94,

065503, doi:10.1103/PhysRevLett.94.065503 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Kadhane, U., Kelkar, A., Misra, D., Kumar, A. & Tribedi, L. C. Effect of giant plasmon

excitations in single and double ionization of C60 in fast heavy-ion collisions. _Physical Review A_ 75, 041201, doi:10.1103/PhysRevA.75.041201 (2007). Article  ADS  Google Scholar  *

Kelkar, A. H., Gulyás, L. & Tribedi, L. C. Angle-differential observation of plasmon electrons in the double-differential cross-section spectra of fast-ion-induced electron ejection from

C60. _Physical Review A_ 92, 052708, doi:10.1103/PhysRevA.92.052708 (2015). Article  ADS  Google Scholar  * Calvayrac, F., Reinhard, P.-G., Suraud, E. & Ullrich, C. A. Nonlinear

electron dynamics in metal clusters. _Physics Reports_ 337, 493–578, doi:10.1016/S0370-1573(00)00043-0 (2000). Article  ADS  CAS  Google Scholar  * Brueckner, K. A. & Thieberger, R.

Nuclear Giant Dipole Resonance. _Physical Review Letters_ 4, 466–468, doi:10.1103/PhysRevLett.4.466 (1960). Article  ADS  Google Scholar  * Biswas, S. & Tribedi, L. C. Plasmon-mediated

electron emission from the coronene molecule under fast ion impact. _Physical Review A_ 92, 060701(R), doi:10.1103/PhysRevA.92.060701 (2015). Article  ADS  Google Scholar  * Boschi, R.,

Clar, E. & Schmidt, W. Photoelectron spectra of polynuclear aromatics. III. The effect of nonplanarity in sterically overcrowded aromatic hydrocarbons. _The Journal of Chemical Physics_

60, 4406–4418, doi:10.1063/1.1680919 (1974). Article  ADS  CAS  Google Scholar  * Mishra, P. M. _et al_. Valence Shell Photoelectron Spectroscopy of Pyrene and Fluorene: Photon Energy

Dependence in the Far-Ultraviolet Region. _Journal of Physical Chemistry A_ 118, 3128–3135, doi:10.1021/jp502445d (2014). Article  ADS  CAS  Google Scholar  * Holm, A. I. S. _et al_. Ions

Colliding with Cold Polycyclic Aromatic Hydrocarbon Clusters. _Physical Review Letters_ 105, 213401, doi:10.1103/PhysRevLett.105.213401 (2010). Article  ADS  CAS  PubMed  Google Scholar  *

Postma, J., Bari, S., Hoekstra, R., Tielens, A. G. G. M. & Schlathölter, T. Ionization and Fragmentation of Anthracene upon Interaction with keV Protons and _α_ Particles. _The

Astrophysical Journal_ 708, 435–444, doi:10.1088/0004-637X/708/1/435 (2010). Article  ADS  CAS  Google Scholar  * Ławicki, A. _et al_. Multiple ionization and fragmentation of isolated

pyrene and coronene molecules in collision with ions. _Physical Review A_ 83, 022704, doi:10.1103/PhysRevA.83.022704 (2011). Article  ADS  Google Scholar  * Martin, S. _et al_. Statistical

fragmentation of doubly charged anthracene induced by fluorine-beam impact at 3 keV. _Physical Review A_ 85, 052715, doi:10.1103/PhysRevA.85.052715 (2012). Article  ADS  Google Scholar  *

Reitsma, G. _et al_. Activation energies for fragmentation channels of anthracene dications - experiment and theory. _Journal of Physics B Atomic Molecular Physics_ 45, 215201,

doi:10.1088/0953-4075/45/21/215201 (2012). Article  ADS  Google Scholar  * Rousseau, P. _et al_. Low-energy ions interacting with anthracene molecules and clusters. _Nuclear Instruments and

Methods in Physics Research B_ 279, 140–143, doi:10.1016/j.nimb.2011.10.050 (2012). Article  ADS  CAS  Google Scholar  * Reitsma, G. _et al_. Ion-polycyclic aromatic hydrocarbon collisions:

kinetic energy releases for specific fragmentation channels. _Journal of Physics B: Atomic, Molecular and Optical Physics_ 46, 245201, doi:10.1088/0953-4075/46/24/245201 (2013). Article  ADS

  Google Scholar  * Gatchell, M. & Zettergren, H. Knockout driven reactions in complex molecules and their clusters. _Journal of Physics B Atomic Molecular Physics_ 49, 162001,

doi:10.1088/0953-4075/49/16/162001 (2016). Article  ADS  Google Scholar  * Micelotta, E. R., Jones, A. P. & Tielens, A. G. G. M. Polycyclic aromatic hydrocarbon processing in

interstellar shocks. _Astronomy and Astrophysics_ 510, A36, doi:10.1051/0004-6361/200911682. (2010). Article  ADS  Google Scholar  * Mishra, P. M., Rajput, J., Safvan, C. P., Vig, S. &

Kadhane, U. Velocity dependence of fragmentation yields in proton-naphthalene collision and comparison with electronic energy loss calculation. _Journal of Physics B: Atomic, Molecular and

Optical Physics_ 47, 085202, doi:10.1088/0953-4075/47/8/085202 (2014). Article  ADS  Google Scholar  * Biswas, S. _et al_. Energy and angular distribution of electrons in ionization of He

and Ne by 6-MeV/u bare carbon ions: Comparison with continuum-distorted-wave eikonal-initial-state calculations in prior and post forms. _Physical Review A_ 90, 052714,

doi:10.1103/PhysRevA.90.052714 (2014). Article  ADS  Google Scholar  * Biswas, S., Monti, J. M., Tachino, C. A., Rivarola, R. D. & Tribedi, L. C. Differential electron emission in the

ionization of Ne and Xe atoms under fast bare carbon ion impact. _Journal of Physics B: Atomic, Molecular and Optical Physics_ 48, 115206, doi:10.1088/0953-4075/48/11/115206 (2015). Article

  ADS  Google Scholar  * Cooper, J. W. Multipole corrections to the angular distribution of photoelectrons at low energies. _Physical Review A_ 42, 6942–6945, doi:10.1103/PhysRevA.42.6942

(1990). Article  ADS  CAS  Google Scholar  * Cooper, J. W. Photoelectron-angular-distribution parameters for rare-gas subshells. _Physical Review A_ 47, 1841–1851,

doi:10.1103/PhysRevA.47.1841 (1993). Article  ADS  CAS  Google Scholar  * Amusia, M. Y., Chernysheva, L. V. & Liverts, E. Z. Angular distributions of secondary electrons in fast

particle-atom scattering. _Physical Review A_ 85, 042722, doi:10.1103/PhysRevA.85.042722 (2012). Article  ADS  Google Scholar  * Biswas, S. _et al_. Electron emission in ionization of He and

Ne by fast dressed oxygen ions and projectile-charge-state dependence. _Physical Review A_ 91, 022711, doi:10.1103/PhysRevA.91.022711 (2015). Article  ADS  Google Scholar  * Biswas, S. _et

al_. Differential electron emission from multi-electronic targets under highly harged bare ion impact. _Journal of Physics: Conference Series_ 635, 022035, doi:10.1088/1742-6596/635/2/022035

(2015). Google Scholar  * Misra, D. _et al_. Double differential distributions of electron emission in ion-atom and electron-atom collisions using an electron spectrometer. _Nuclear

Instruments and Methods in Physics Research B_ 267, 157–162, doi:10.1016/j.nimb.2008.10.091 (2009). Article  ADS  CAS  Google Scholar  * Champion, C. _et al_. Theoretical predictions for

ionization cross sections of DNA nucleobases impacted by light ions. _Physics in Medicine and Biology_ 55, 6053–6067, doi:10.1088/0031-9155/55/20/002 (2010). Article  ADS  CAS  PubMed 

Google Scholar  * Dal Cappello, C. _et al_. Theoretical and experimental investigations of electron emission in C6+ + H2O collisions. _Nuclear Instruments and Methods in Physics Research B_

267, 781–790, doi:10.1016/j.nimb.2008.12.010 (2009). Article  ADS  CAS  Google Scholar  * Champion, C., Boudrioua, O., Dal Cappello, C., Sato, Y. & Ohsawa, D. Theoretical and

experimental investigations of electron emission in He2++H2O collisions. _Physical Review A_ 75, 032724, doi:10.1103/PhysRevA.75.032724 (2007). Article  ADS  Google Scholar  * Boudrioua, O.,

Champion, C., Dal Cappello, C. & Popov, Y. V. Ab initio calculation of differential and total cross sections for the ionization of water vapor by protons. _Physical Review A_ 75,

022720, doi:10.1103/PhysRevA.75.022720 (2007). Article  ADS  Google Scholar  * Belkić, D., Gayet, R. & Salin, A. Electron capture in high-energy ion-atom collisions. _Physics Reports_

56, 279–369, doi:10.1016/0370-1573(79)90035-8 (1979). Article  ADS  Google Scholar  * Frisch, M. J. T. Gaussian 09, Revision A.02. _Gaussian_, _Inc_., _Wallingford CT_ (2009). * Fainstein,

P. D., Ponce, V. H. & Rivarola, R. D. Two-centre effects in ionization by ion impact. _Journal of Physics B: Atomic, Molecular and Optical Physics_ 24, 3091–3119,

doi:10.1088/0953-4075/24/14/005 (1991). Article  ADS  CAS  Google Scholar  * Stolterfoht, N., DuBois, R. D. & Rivarola, R. D. _Electron Emission in Heavy Ion_-_Atom Collisions_.

Springer-Verlag, Berlin (1997). * Fainstein, P. D., Ponce, V. H. & Rivarola, R. D. A theoretical model for ionisation in ion-atom collisions. Application for the impact of multicharged

projectiles on helium. _Journal of Physics B: Atomic, Molecular and Optical Physics_ 21, 287–299, doi:10.1088/0953-4075/21/2/013 (1988). Article  ADS  CAS  Google Scholar  * Galassi, M. E.,

Rivarola, R. D., Beuve, M., Olivera, G. H. & Fainstein, P. D. Theoretical calculation of single ionization in collisions between protons and low-Z molecules at intermediate and high

energies. _Physical Review A_ 62, 022701, doi:10.1103/PhysRevA.62.022701 (2000). Article  ADS  Google Scholar  * Galassi, M. E., Rivarola, R. D. & Fainstein, P. D. Multicenter character

in single-electron emission from H2 molecules by ion impact. _Physical Review A_ 70, 032721, doi:10.1103/PhysRevA.70.032721 (2004). Article  ADS  Google Scholar  * Clementi, E. _IBM Journal

of Research and Development_, _Special Supplement_ 9, 2 (1965). Download references ACKNOWLEDGEMENTS The authors would like to thank the staffs at the BARC-TIFR Pelletron accelerator

facility for smooth operation of the machine. We thank D. Misra for his various helps during the measurements. P.F.W would like to thank the Sandia National Laboratories which is a

multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S.

Department of Energy’s National Nuclear Security Administration under Contract DE-NA0003525. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Tata Institute of Fundamental Research, Department

of Nuclear and atomic Physics, Homi Bhabha Road, Colaba, Mumbai, 400 005, India Shubhadeep Biswas & Lokesh C. Tribedi * Université Bordeaux 1, CNRS/IN2P3 Centre d’Études Nucléaires de

Bordeaux Gradignan (CENBG) Chemin du Solarium, BP120, 33175, Gradignan, France Christophe Champion * Sandia National Laboratories, Albuquerque, New Mexico, 87185, USA P. F. Weck Authors *

Shubhadeep Biswas View author publications You can also search for this author inPubMed Google Scholar * Christophe Champion View author publications You can also search for this author

inPubMed Google Scholar * P. F. Weck View author publications You can also search for this author inPubMed Google Scholar * Lokesh C. Tribedi View author publications You can also search for

this author inPubMed Google Scholar CONTRIBUTIONS L.C.T. had the idea and planned this experiment. L.C.T. and S.B. executed the experiment, analysis and interpretation. C.C. and P.F.W.

provided the model calculations in which P.F.W. provided the wave functions of the molecules whereas C.C. contributed towards the CB1 model calculations. L.C.T., S.B. and C.C. prepared the

paper which was reviewed by all the authors. CORRESPONDING AUTHOR Correspondence to Lokesh C. Tribedi. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare that they have no competing

interests. ADDITIONAL INFORMATION CHANGE HISTORY: A correction to this article has been published and is linked from the HTML version of this paper. The error has been fixed in the paper.

PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. A correction to this article is available online at

https://doi.org/10.1038/s41598-017-17041-6. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Biswas, S., Champion, C., Weck, P.F. _et al._ Differential electron emission from polycyclic aromatic hydrocarbon molecules under fast ion

impact. _Sci Rep_ 7, 5560 (2017). https://doi.org/10.1038/s41598-017-05149-8 Download citation * Received: 31 January 2017 * Accepted: 24 May 2017 * Published: 17 July 2017 * DOI:

https://doi.org/10.1038/s41598-017-05149-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative