The ribosome lowers the entropic penalty of protein folding

ABSTRACT Most proteins fold during biosynthesis on the ribosome1, and co-translational folding energetics, pathways and outcomes of many proteins have been found to differ considerably from

those in refolding studies2,3,4,5,6,7,8,9,10. The origin of this folding modulation by the ribosome has remained unknown. Here we have determined atomistic structures of the unfolded state

of a model protein on and off the ribosome, which reveal that the ribosome structurally expands the unfolded nascent chain and increases its solvation, resulting in its entropic

destabilization relative to the peptide chain in isolation. Quantitative 19F NMR experiments confirm that this destabilization reduces the entropic penalty of folding by up to 30 kcal mol−1

and promotes formation of partially folded intermediates on the ribosome, an observation that extends to other protein domains and is obligate for some proteins to acquire their active

conformation. The thermodynamic effects also contribute to the ribosome protecting the nascent chain from mutation-induced unfolding, which suggests a crucial role of the ribosome in

supporting protein evolution. By correlating nascent chain structure and dynamics to their folding energetics and post-translational outcomes, our findings establish the physical basis of

the distinct thermodynamics of co-translational protein folding. SIMILAR CONTENT BEING VIEWED BY OTHERS THE RIBOSOME STABILIZES PARTIALLY FOLDED INTERMEDIATES OF A NASCENT MULTI-DOMAIN

PROTEIN Article Open access 04 August 2022 NASCENT CHAINS DERIVED FROM A FOLDABLE PROTEIN SEQUENCE INTERACT WITH SPECIFIC RIBOSOMAL SURFACE SITES NEAR THE EXIT TUNNEL Article Open access 29

May 2024 INTERACTIONS BETWEEN NASCENT PROTEINS AND THE RIBOSOME SURFACE INHIBIT CO-TRANSLATIONAL FOLDING Article Open access 14 October 2021 MAIN Most proteins fold co-translationally during

biosynthesis on the ribosome1. There is increasing evidence of a direct role for the ribosome in regulating folding of the nascent chain2,3,4,5,6,7,8,9,10, with increasing clarity on how it

interacts with the elongating nascent chain7,11,12,13, which is thought to contribute to alterations to nascent chain thermodynamic stability6,7,8,9,10 and folding and unfolding rates5,8.

Consequently, co-translational folding (coTF) differs from in vitro refolding studies of analogous, isolated counterparts3,5,6,14,15,16, with unique intermediate conformations in

coTF3,5,6,14,15,17, folding in the absence of the complete protein sequence4,14, and the ability of the ribosome to mitigate misfolding-prone destabilizing mutations4 among the many

discriminating observations whose origins remain poorly understood. This is a crucial gap in our understanding of proteostasis as many proteins reach an active conformation following coTF,

whereas post-translational unfolding–refolding in the cell is generally avoided owing to high kinetic stabilities, and when proteins are unfolded (in vitro), they often do not refold

spontaneously, but instead misfold and aggregate1,18,19. In contrast to refolding studies, the unfolded state on the ribosome exists under native conditions7, and is adopted by all proteins

during early biosynthesis. The ribosome-bound unfolded state has not been characterized in structural detail owing to technical challenges, yet is likely to be crucial to understanding

folding thermodynamics and pathways20,21,22. Here, using paramagnetic relaxation enhancement (PRE) NMR spectroscopy (PRE-NMR) combined with atomistic molecular dynamics simulations, we have

determined structural ensembles of the unfolded state and found that the ribosome structurally expands the conformational ensemble. We infer an entropically driven destabilization of the

unfolded state on the ribosome relative to in isolation arising primarily from the increased solvation of the more expanded ensemble. Experiments show that this results in the ribosome

reducing the entropic penalty of protein folding by up to around 30 kcal mol−1. Despite previous suggestions that interactions between nascent chains and the ribosome surface influence

folding kinetics and thermodynamics5,6,7, we show here that these interactions account for a minor fraction of the energetic changes observed between protein folding on and off the ribosome.

Instead, we establish that the entropic destabilization of the unfolded state provides the fundamental basis for why protein folding on the ribosome is distinct to refolding in vitro.

STRUCTURES OF THE UNFOLDED STATE We investigated the unfolded state of a model immunoglobulin-like domain, FLN52,6,7,11,23,24,25, and determined a set of structural ensembles on and off the

ribosome. FLN5 folds reversibly in isolation, thus also facilitating detailed, quantitative comparisons of post-translational folding versus coTF thermodynamics6,7,11,23,24. The variant FLN5

A3A3 (Extended Data Fig. 1a) enables the characterization by NMR of conformational and dynamic preferences of unfolded FLN5 without the complication of folding7,24. For the ribosome–nascent

chain complex (RNC), FLN5 A3A3 is tethered to the ribosome peptidyl transferase centre (PTC) via a 31-amino acid linker (FLN5+31 A3A3), comprising the subsequent FLN6 domain and SecM

stalling sequence (Extended Data Fig. 1a). This construct has the entire FLN5 sequence emerged from the ribosomal exit tunnel and is the earliest linker length at which some folding is

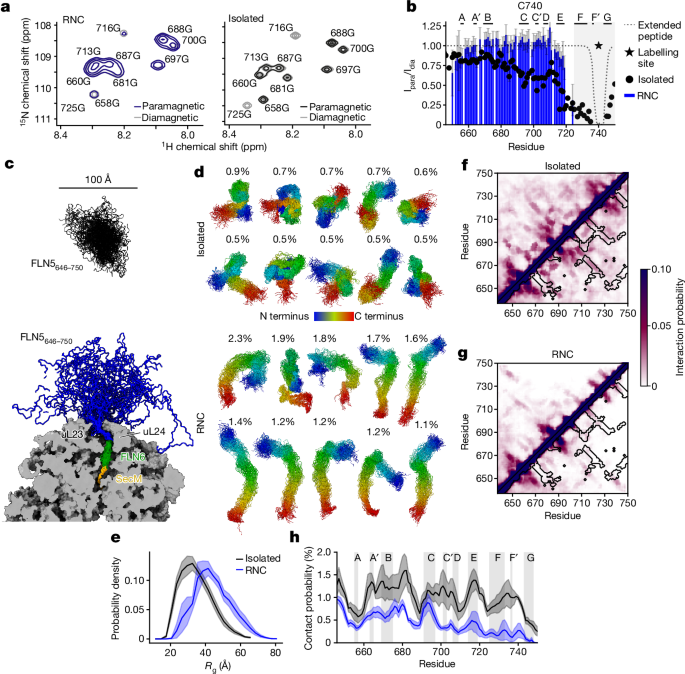
observed in wild-type FLN56,11. PRE-NMR experiments of FLN5 A3A3 showed less broadening for the RNC compared with the isolated proteins (Fig. 1a,b, Extended Data Figs. 1 and 2 and Methods),

suggesting that the conformational ensemble is less compact on the ribosome (Supplementary Notes 1–4). Restraints obtained from these experiments were used to reweight all-atom molecular

dynamics simulations with explicit solvent of the unfolded states (Methods and Supplementary Notes 5–7). Molecular dynamics simulations of the isolated protein were initially used to

identify a suitable force field for this protein (Extended Data Fig. 3 and Supplementary Note 5) and were subsequently validated against the radius of hydration (_R_h), NMR chemical shifts,

residual dipolar couplings (RDCs) and small-angle X-ray scattering (SAXS) data (Extended Data Fig. 4 and Supplementary Note 6). The simulations exhibited good convergence with respect to the

overall compactness, secondary structure and long-range contacts in the ensembles (Supplementary Note 7). The reweighted structural ensembles are in good agreement with both the PRE-NMR and

validation data on and off the ribosome (Extended Data Figs. 4 and 5). Both structural ensembles of the unfolded state on and off the ribosome display heterogeneity (Fig. 1c,d). An analysis

of the main structural clusters reveals that the isolated ensemble samples more compact and spherical states (Fig. 1d and Extended Data Fig. 6i) with the radius of gyration of the nascent

chain increasing by approximately 26% on the ribosome from 34.9 ± 1.0 Å to 44.1 ± 1.8 Å (Fig. 1e). This structural expansion (throughout this Article, ‘expansion’ refers to structural

expansion) of the ensemble is partly caused by steric exclusion from and tethering to the ribosome, but additional factors also contribute (Supplementary Note 8). Owing to the expansion, the

amount of β-strand secondary structure in the RNC ensemble decreases along the entire sequence from 3.2 ± 0.5% to 1.1 ± 0.3% in total (Extended Data Fig. 5f) and fewer contacts are observed

compared with the isolated protein (0.4 ± 0.1% and 1.0 ± 0.2% on average, respectively; Fig. 1h). Most of these transient contacts are non-native (Fig. 1f,g) and only 1.4 ± 0.2% and 1.0 ± 

0.1% of native contacts are formed off and on the ribosome, respectively. Long-range contacts are particularly reduced at the C terminus (residues N730–G750) of FLN5 A3A3 (Fig. 1h), which in

turn is bound to the ribosome surface around 80% of the time7 (Extended Data Fig. 5g,h). These nascent chain–ribosome interactions are driven predominantly by electrostatic effects and

mediated via ribosomal RNA and RNA-bound Mg2+ ions (Extended Data Fig. 5i,j), whereas contacts within the unfolded protein itself occur more frequently between hydrophobic amino acids

(Extended Data Fig. 5k). This structural analysis demonstrates that the ribosome significantly affects the global structural properties of the unfolded state. ENTROPIC DESTABILIZATION ON THE

RIBOSOME We utilized our structures of the unfolded state on and off the ribosome to estimate their effect on folding energetics from an enthalpic (Δ_H_) and entropic (Δ_S_) point of view,

both of which determine the folding free energy (Δ_G_ = Δ_H_ – _T_Δ_S_). Ribosome interactions have been shown to modulate folding thermodynamics and these interactions with the unfolded

FLN5+31 A3A3 nascent chain result in a destabilization of the folding free energy7 (ΔΔ_G_N-U,RNC-iso; where N, U, and iso are native state, unfolded state and isolated protein, respectively)

by +1 kcal mol−1. We explored whether the overall entropy of the unfolded state changes on the ribosome compared to off the ribosome (Δ_S_RNC-iso). Using our molecular dynamics ensembles,

we analysed the protein conformational entropy (Δ_S_conf) and solvation entropy (Δ_S_solv) (Methods), which together comprise the total entropy change (Δ_S_ = Δ_S_conf + Δ_S_solv). A

residue-specific analysis of the unfolded state shows distinct expanded regions on the ribosome (having an increased local radius of gyration; Fig. 2a). The same nascent chain regions (for

example, residues G700–N740) also show a significant reduction in the conformational entropy on the ribosome (Fig. 2b) and more restricted sampling of the Ramachandran map (Extended Data

Fig. 6e), which is consistent with a more elongated shape of the nascent chain ensemble26 (Fig. 1b and Extended Data Fig. 6h). We observed this decrease in conformational entropy

orthogonally through a cluster analysis, revealing fewer accessible conformational states on the ribosome relative to off the ribosome (Extended Data Fig. 6a,b). Notably, the entropic

destabilization is observed even for residues distal to the ribosome (for example, V664–I674), showing that the ribosome exerts a long-range entropic effect that arises from more than

ribosome interactions alone (Fig. 2b). The conformational restriction imposed by the ribosome is estimated to globally destabilize the unfolded state relative to the isolated unfolded

protein (−_T_Δ_S_RNC-iso,conf) by at least +2 kcal mol−1 at 298 K (Methods and Extended Data Fig. 6g). An increase in solvation entropy has long been described as the major driving force of

the hydrophobic collapse in protein folding27. The solvation entropy of the unfolded state was thus explored by analysing the solvent-accessible surface area (SASA) of FLN5. The SASA was

significantly increased on the ribosome compared to off the ribosome (+6 ± 1 nm2 in total; Extended Data Fig. 6i), particularly in regions where the nascent chain is locally expanded (Fig.

2c). On the basis of the changes in SASA, we estimated the resulting solvent entropy changes (Methods and Supplementary Note 9). These calculations show a reduced solvation entropy which

further destabilizes the unfolded state on the ribosome (−_T_Δ_S_RNC-iso,solv) by +11 ± 4 kcal mol−1 at 298 K. Both the conformational and solvation entropy are thus globally reduced

throughout the RNC ensemble (Fig. 2d,e). This results in a combined entropic destabilization of 13 ± 4 kcal mol−1, outcompeting both enthalpic gains in stability due to ribosome interactions

and increased solvation (Δ_H_RNC-iso,solv = −3 ± 4 kcal mol−1). The net increase in free energy of the unfolded state on compared to off the ribosome is therefore expected to be +9 ± 6 kcal

 mol−1 (Fig. 2f) at this nascent chain length. The strong contribution of solvation entropy effects was also verified using direct entropy calculations, resulting in an estimate of

approximately 30 ± 10 kcal mol−1 at 298 K (Supplementary Note 10). MEASUREMENTS OF FOLDING THERMODYNAMICS To experimentally consider these entropic effects, we sought to determine Δ_S_ and

Δ_H_ of folding by investigating the temperature dependence of folding for wild-type FLN5. The FLN5+34 RNC and the C-terminal truncation FLN5Δ6 variant24 as the analogous isolated protein

were selected, both of which enable the simultaneous observation of the unfolded and native states by 19F NMR spectroscopy6 within the same temperature range (278 K–303 K). Under these

conditions, we also observe two folding intermediates in the FLN5+34 RNC (I1 and I2) and one intermediate in the isolated FLN5Δ6 variant6,24 (Iiso) (Fig. 2g and Extended Data Fig. 7a,b). The

1D 19F NMR spectra were fitted to determine the population of each species, enabling quantification of thermodynamic parameters from a nonlinear fit of the equilibrium constant as a

function of temperature (Fig. 2h and Methods). Both on and off the ribosome, the apparent enthalpy of folding (Δ_H_N-U) is negative, whereas the apparent entropy of folding (−_T_Δ_S_N-U) is

positive—that is, the folding reaction is enthalpy-driven to compensate for an unfavourable entropic penalty. The heat capacity of folding (Δ_C_p,N-U) obtained for the isolated protein (−1.7

± 0.3 kcal mol−1 K−1) is as expected on the basis of protein size28 (−1.5 ± 0.2 kcal mol−1 K−1), but increases on the ribosome (ΔΔ_C_p,N-U,RNC-iso = +0.9 ± 0.4 kcal mol−1 K−1), presumably

owing to the increased water ordering and local ion concentration near the ribosome surface29. These experiments also show the temperature dependence of folding of the RNC to be

significantly attenuated compared to the corresponding isolated protein (Fig. 2g,h) with the magnitudes of Δ_H_ and −_T_Δ_S_ being strongly reduced on the ribosome (ΔΔ_H_N-U,RNC-iso = +32.9

± 3.2 kcal mol−1, −_T_ΔΔ_S_N-U,RNC-iso = −34.5 ± 3.2 kcal mol−1 at 298 K; Fig. 2i). Folding on the ribosome is consequently less enthalpically driven but also exhibits a lower entropic

penalty (Fig. 2i). The reduction in −_T_Δ_S_ on the ribosome experimentally confirms the predicted entropic destabilization of the unfolded state and is within the range of the estimated

solvation entropy change based on a solvation analysis of our molecular dynamics ensembles (30 ± 10 kcal mol−1; Supplementary Note 10). Of note, folding from the intermediate state(s) to the

native state is only marginally sensitive to temperature, both on and off the ribosome (Extended Data Fig. 7c,d), corroborating that the entropic differences originate predominantly from

modulation of the unfolded state. The less negative Δ_H_ on the ribosome must therefore predominantly result from the destabilization of the native state on the ribosome relative to off the

ribosome6 (Supplementary Note 11). Our thermodynamic experiments thus clearly show that the expansion of the unfolded state results in the lowering of the entropic penalty of folding

relative to the isolated protein. ENTROPY EFFECTS ARE SEQUENCE-INDEPENDENT Given the strong interactions of the unfolded FLN5 nascent chain with the negatively charged ribosome surface as

observed in our structures, we next examined its effect on the large folding enthalpy and entropy differences on and off the ribosome. We performed 19F NMR experiments of a polyglutamate

mutant (E6) (Extended Data Fig. 7e,f), which has reduced ribosome interactions7 (from 85 ± 5% to 10 ± 2%). Large changes in folding enthalpy and entropy (relative to an analogous isolated

protein) are still observed and only marginally reduced relative to wild-type (ΔΔ_H_N-U,RNC-iso = +22.6 ± 5.5 kcal mol−1, −_T_ΔΔ_S_N-U,RNC-iso = −20.6 ± 5.5 kcal mol−1 at 298 K, Extended

Data Fig. 7g,h). These results show that ribosome interactions only partially contribute to the large change in coTF energetics. This is consistent with the entropic effects originating

predominantly from the increased hydration of the expanded nascent chain (Fig. 2f), suggesting that this phenomenon may be sequence-independent. PERSISTENCE DURING BIOSYNTHESIS We reasoned

that the structural expansion of the unfolded state and re-balanced enthalpy–entropy of coTF should decrease in magnitude as the nascent chain elongates and the distance between FLN5 and the

ribosome surface increases. To test this, we performed PRE-NMR experiments on the unfolded nascent chain of two longer FLN5 RNCs (FLN5+47 A3A3 and FLN5+67 A3A3; Extended Data Fig. 8a–c).

The measured PRE intensity ratios decrease with increasing nascent chain length (Fig. 3a), showing that the expansion decreases as expected (see Supplementary Note 2). However, the intensity

ratios remain higher than those of the isolated protein, indicating that the unfolded nascent chain remains more expanded on the ribosome at all RNC lengths tested, highlighting the

long-range effect that the ribosome exerts on nascent chain structure. We next measured the enthalpy and entropy of folding of FLN5+67 using our 19F NMR approach (Fig. 3b and Extended Data

Fig. 8d–i). Correlating with the decreased structural expansion of the unfolded state at FLN5+67 (relative to FLN5+31), we observed that the change in folding entropy on the ribosome

persists but is reduced from −34.5 ± 3.2 kcal mol−1 at FLN5+34 to −10.1 ± 2.8 kcal mol−1. Likewise, the enthalpy of folding becomes more favourable as the nascent chain elongates from

FLN5+34 to FLN5+67 and the native state becomes less destabilized further away from the ribosome surface6,9,30,31. We conclude that the thermodynamic effects persist during biosynthesis but

progressively decrease in magnitude. These experiments also establish a direct relationship between the structure of the unfolded nascent chain and coTF thermodynamics. We then explored

whether the entropic destabilization of the unfolded nascent chain during biosynthesis could rationalize the observed differences in the folding of FLN5 on and off the ribosome, common to

other proteins3,5,8,9,10,17,30,31,32,33. Whereas the native state is destabilized on the ribosome relative to the native state in isolation6,7,25 (Extended Data Fig. 7i–k), FLN5

paradoxically populates two coTF intermediates that are significantly more stable than the single intermediate found in isolation (Iiso of FLN5∆6; Fig. 2g) and which are completely

undetectable in full-length isolated FLN56,24. The stabilities of the coTF intermediates are modulated by the nascent chain length, such that at FLN5+47, their stabilities are more than 4 

kcal mol−1 greater than that of Iiso (relative to their respective unfolded states6) (Fig. 3c). We quantified the contribution of ribosome binding to stabilizing the coTF intermediates by

estimating the population of intermediates bound to the ribosome surface based on their measured rotational correlation times—that is, how fast the domain tumbles in solution (Extended Data

Fig. 8j–p and Methods). These experiments indicate that such binding can only account for less than 0.1 kcal mol−1 of stabilization on the ribosome at FLN5+47 (Fig. 3c). Therefore, ribosome

interactions contribute only weakly to stabilizing coTF intermediates. These measurements are also consistent with the observed persistence of the intermediates within a broad folding

transition6 (that is, from approximately FLN5+31 to FLN5+67) and in a range of conditions that disrupt or reduce ribosome–nascent chain interactions, including changes in the distance from

the ribosome (Fig. 3c), high concentrations of salt and urea, nascent chain and ribosome surface mutations2,6 (Extended Data Fig. 7e–h), and temperature (Fig. 2g,h). We next built a model of

the free energies of coTF by comparison to the isolated protein. As the most stable intermediate off the ribosome, Iiso, is structurally similar to I2 (ref. 6), we used our measurements of

binding energies (Fig. 3c) to link the relative free energies of FLN5 on and off the ribosome (Fig. 3d). From this thermodynamic analysis, we can infer that the unfolded state in the FLN5+42

RNC (the longest linker length at which an unfolded population is observed6) is destabilized by at least 2.7 kcal mol−1 relative to the isolated unfolded protein (ΔΔ_G_U,RNC-iso; Fig. 3d).

Together, we conclude that the ribosome persistently destabilizes unfolded and folded FLN5 during biosynthesis to promote the formation of partially folded intermediates. THERMODYNAMIC

EFFECTS ACROSS PROTEINS As the entropic effects are at least partly sequence-independent (Extended Data Figs. 5l,m and 7), we examined whether the reduction of the folding entropy penalty on

the ribosome and its implications for coTF are also observed for other proteins. We investigated the folding of a structurally homologous domain, titin I27 (the 27th immunoglobulin-like

domain of titin; Fig. 4a) and the common oncoprotein HRAS34, a GTPase protein with an α/β-fold35 (Fig. 4b). In isolation, I27 has been shown to fold reversibly36, which, as for FLN5, enables

thermodynamic comparisons of folding on and off the ribosome. I27 exhibits two-state folding behaviour in urea (Fig. 4c) but populates one high-energy intermediate in a destabilized mutant

(Iiso; Extended Data Fig. 9a). Although a previous study suggested that the ribosome does not affect folding of I2737, our results show two folding intermediates being stabilized on the

ribosome (Fig. 4c, I1 and I2). Similarly, 19F NMR spectra of HRAS also show the population of stable coTF intermediates, even before complete translation, that are not populated in isolation

(Fig. 4d). The coTF intermediates of both proteins are partially folded, since they are completely destabilized by mutations that disrupt the native hydrophobic core37 (Extended Data Fig.

9c,e,f). Furthermore, as observed for FLN5, the temperature dependence of folding is reduced for I27 on the ribosome (Fig. 4e,f and Extended Data Fig. 9a,b), with a reduced enthalpy of

folding (ΔΔ_H_N-U,RNC-iso = +28.8 ± 10.1 kcal mol−1 at 298 K) and a lower entropic penalty of at least 18 kcal mol−1 on the ribosome (−_T_ΔΔ_S_N-U,RNC-iso = −28.5 ± 10.1 kcal mol−1 at 298 

K). Folding from the unfolded state to the first HRAS intermediate (I1, HRAS1–81 RNC) is similarly temperature-insensitive (Fig. 4g and Extended Data Fig. 9d) and exhibits an entropic

penalty (−_T_Δ_S_I1-U) of only +5.0 ± 2.0 kcal mol−1 (Fig. 4h). The thermodynamic effects reported in this work and the resulting population of stable coTF intermediates thus appear to be a

general phenomenon. Given the differences in folding thermodynamics and pathways on and off the ribosome, we sought to examine how coTF events may determine the post-translational fate of

nascent proteins. Whereas our model systems FLN5 and I27 have been shown to fold reversibly to their native state in isolation36,38, many proteins are not able refold off the

ribosome1,18,19. Indeed, the proteolytic stability of the KRAS isoform has been found to be modulated by codon usage39, and so we examined whether the acquisition of native HRAS structure is

also dependent on its coTF pathway. Consistent with prior observations on KRAS, refolded isolated HRAS showed reduced proteolytic stability compared with control or native HRAS (Extended

Data Fig. 9h), which also persisted when refolded in eukaryotic cell lysate (Extended Data Fig. 9i). A residue-specific analysis by 1H,15N NMR shows that refolded HRAS forms a native-like,

GDP-bound conformation, consistent with prior biophysical experiments40, but distinct structural regions, including the switch 2 region that is involved in nucleotide exchange41, show

increased NMR signal intensities—that is, probably altered backbone dynamics (Extended Data Fig. 9j). Indeed, when assessing HRAS function with a GDP/GTP nucleotide exchange assay, we found

that refolded HRAS is completely inactive, whereas HRAS purified from cells and the HRAS+20GS RNC are both active (Extended Data Fig. 9g). Subtle differences in structure and dynamics thus

alter the fate of refolded HRAS, which appears to be kinetically trapped in an inactive state. These results show that the thermodynamic modulation by the ribosome and resulting coTF pathway

appear to be obligate to the formation of functionally active HRAS. MUTATIONS ARE BUFFERED ON THE RIBOSOME We hypothesized that the ribosome additionally modulates the effect of

destabilizing mutations4. To test this, we designed nine variants of FLN5 that include disruptions to the hydrophobic core, proline isomerization24 and electrostatic charge7. For all

mutants, we measured the folding free energy on and off the ribosome using 19F NMR (Fig. 5a,b and Extended Data Fig. 10a,b,h,i). The mutants exhibited a wide range of stabilities (Δ_G_N-U)

from −0.7 to −5.4 kcal mol−1 off the ribosome (equal to a 4.7 ± 0.3 kcal mol−1 range in stabilities). However, on the ribosome, the stabilities of the mutants exhibited a narrower range of

1.5 ± 0.1 kcal mol−1 (Fig. 5a) and were all less destabilizing (ΔΔΔ_G_N-U) by 0.3–3.7 kcal mol−1 (Fig. 5b). We speculated that the re-balanced enthalpy–entropy compensation contributes to

this buffering effect. Given the large contribution from increased nascent chain solvation (Fig. 2f), we also measured the destabilization of four hydrophobic mutants in the presence of 2.5 

M urea (Extended Data Fig. 10c); urea weakens the hydrophobic effect by displacing several water molecules from the protein solvation shell42,43. By effectively reducing the gains in

solvation of the unfolded RNC, we find that the mutations are less strongly buffered in urea (Fig. 5c). In agreement with this, the differences in entropy and enthalpy of folding on the

ribosome (relative to the isolated protein) are reduced in urea compared with in pure water (Fig. 5d and Extended Data Fig. 10e–g). Thus, the magnitude and extent of mutation buffering

correlates with the reduced temperature dependence of protein folding on the ribosome. We conclude that an additional consequence of the destabilized unfolded and folded states is to buffer

and therefore mitigate the effect of destabilizing mutations during coTF folding. DISCUSSION Here we have determined an atomistic structural ensemble of a nascent, unfolded protein tethered

to the ribosome, analysed its differences to the protein in isolation, and studied its implications for coTF. Our structures reveal that the unfolded state on the ribosome is more

structurally expanded and samples fewer long-range contacts than off the ribosome. The ribosome thus has a key role in shaping the conformational space of the emerging nascent chain. The

expansion and increased solvation of the unfolded state on the ribosome (Fig. 6) result in reduced conformational and water entropies, a finding that constrasts with previous theoretical

studies44,45. The entropic destabilization observed in the unfolded nascent chain relative to the isolated protein outcompetes the enthalpic stabilization provided by electrostatic ribosome

interactions7 and increased solvation (Fig. 2f). Meanwhile, the native state structure or environment is perturbed (Extended Data Fig. 7i,j) and enthalpically destabilized on the ribosome

relative to its isolated form6 (Figs. 2i and 3d), probably owing to the space constraints near the exit vestibule30 and long-range electrostatic effects from the negatively charged ribosome

surface9,31. Together, these effects result in a marked re-balancing of the enthalpy–entropy compensation for protein folding that occurs on the ribosome (Fig. 6). The re-balanced

enthalpy–entropy compensation of coTF folding provides a physical rationale for understanding differences in the folding on and off the ribosome. It enables nascent proteins to fold via

distinct partially folded intermediates on the ribosome that are absent or significantly less stable in isolation6,24, as observed for multiple proteins3,6,14,15,17,32,33 including all three

model systems in this work (Figs. 3 and 4). Although the biological effect could be reduced for small proteins that unfold and refold post-translationally, the substantial physical,

thermodynamic changes on the ribosome are likely to affect the entire folded proteome during biosynthesis. Indeed, our analyses reveal that the expansion and destabilization of the unfolded

state is partially caused by the physical effects of steric exclusion and tethering (Extended Data Fig. 5l,m) and is not dependent on sequence-specific ribosome–nascent chain interactions

(Extended Data Fig. 7e–h). The ribosome can therefore act as a universal foldase, that in contrast to others is ATP-independent, and can promote the formation of functionally active

proteins, many of which do not spontaneously unfold and refold off the ribosome1,18,19, including HRAS (Extended Data Fig. 9g–j). The distinct thermodynamics of nascent chains may benefit

other co-translational processes that are also entropically disfavoured, such as chaperone binding46,47, translocation47 or protein assembly47,48,49. The high stabilities of coTF

intermediates across a wide folding transition, as observed for FLN56,24 and HRAS (Fig. 4d), may additionally provide a longer time frame for such processes to occur. Conversely, partially

folded intermediates may result in the formation of non-productive states, such as off-pathway or misfolded species4,50,51,52, highlighting that in the cellular environment there is indeed a

fine line between folding and misfolding on the ribosome. Finally, we present quantitative evidence of mutation buffering by the ribosome as an additional consequence of the thermodynamic

effects occurring co-translationally. Throughout evolution proteins diversify through mutations, most of which are destabilizing and impose limits on evolvability while maintaining a fold

and function53,54. Many destabilizing mutants studied here would be expected to be fully unfolded co-translationally in the absence of buffering, despite being completely natively folded in

isolation (Extended Data Fig. 10h), because folded structure is less stable on the ribosome (Fig. 3d). The buffering effect thus minimizes the increased population of unfolded nascent chain

resulting from a destabilizing mutation, effectively promoting coTF over post-translational folding and averting potentially harmful consequences for mutant proteins. For example,

accumulation of unfolded populations on the ribosome and failure of coTF have been linked to co-translational ubiquitination and degradation of nascent chains55. Additionally, lack of coTF

could be detrimental for nascent chains that rely on co-translational complex assembly (more than 20% of the proteome48), chaperone engagement46, or cannot fold into an active conformation

post-translationally1,18,19 (Extended Data Fig. 9g–j). Notably, cellular chaperones have also been implicated in mutation buffering and their availability has been linked to the rate at

which proteins evolve53,56,57,58,59,60. CoTF may therefore also have a universal role in mutation buffering and evolution during the initial stages of protein folding before transferring

nascent chains to chaperones47. In conclusion, we have demonstrated that the ribosome entropically destabilizes the unfolded state. This provides a general, physical explanation for the

fundamental differences in protein folding pathways and energetics observed in vitro versus on the ribosome. Beyond the effects of steric exclusion and tethering, other factors that

contribute to the destabilization of the unfolded and native states on the ribosome remain unexplored. Deeper insights may decipher additional physical principles behind what we propose to

be a universal phenomenon during de novo protein folding. METHODS PROTEIN EXPRESSION AND PURIFICATION DNA constructs of FLN5 were previously described7,11. Coding sequences for titin I27 and

HRAS were introduced into the pLDC-17 vector using standard procedures. Further mutations were introduced using site-directed mutagenesis; for 19F labelling, amber stop codons were

introduced6 in position 32 in HRAS, and residue 14 with an additional K87H point mutation in I27. FLN5 variants were expressed as His-tagged proteins and isotopically labelled in

_Escherichia coli_ BL21 DE3-Gold cells as previously described6,7; an identical protocol was used to produce purified samples of I27 and HRAS. RNC constructs comprised an arrest-enhanced

variant of the SecM stalling sequence, FSTPVWIWWWPRIRGPP, as previously described6. Purification of isolated FLN5 A3A3 was performed by affinity chromatography followed by size-exclusion

chromatography in the presence of 6 M urea prior to buffer exchange into Tico buffer (10 mM Hepes, 30 mM NH4Cl, 12 mM MgCl2, 1 mM EDTA). The full protein sequence of the FLN5 A3A3 is

deposited together with its chemical shift assignment on the BMRB (entry 51023). For the RDC, pulse-field gradient NMR (PFG-NMR) and PRE-NMR experiments, the additional mutation C747V

(referred to FLN5 A3A3 V747) was introduced to yield a cysteine-less construct for site-specific spin labelling. The protein concentration was determined using the BCA assay according to the

manufacturer’s instructions. RNCs were expressed, isotopically labelled uniformly with 15N, or site-specifically with 19F, and purified as previously described6,7. For samples for

intermolecular PRE-NMR experiments involving ribosome labelling, we generated modified _E. coli_ BL21 strains with cysteine mutations in uL23 and uL24 using CRISPR as previously described2.

RNC samples were prepared in Tico buffer for experiments. Western blot analyses were undertaken with an anti-hexahistidine horseradish peroxidase-linked antibody (Invitrogen, 1:5,000

dilution). FLUORESCENT AND PEG-MALEIMIDE LABELLING OF 70S AND RNC SAMPLES Ribosomes and RNCs were first reduced using 2 mM TCEP overnight at 277 K, then buffer exchanged into labelling

buffer. For fluorescein-5-maleimide and PEG-maleimide, labelling was performed in Tico at pH 7.5. ABD-MTS labelling was performed in labelling buffer (50 mM HEPES, 12 mM MgCl2, 20 mM NH4Cl,

1 mM EDTA, pH 8.0). Samples were labelled using a 10x molar excess of ABD-MTS, or fluorescein-5-maleimide. Cysteine mass-tagging by PEGylation was performed as previously described with

10,000-fold molar excess of PEG over sample7. ABD-MTS and PEGylation reactions were analysed using 12% Bis-Tris SDS–PAGE gels61. The fluorescein-labelled reactions were run on a 20% Tricine

SDS–PAGE gel, modified from ref. 62. NMR SPECTROSCOPY All NMR experiments were recorded with Topspin 3.5pl2. NMR experiments of FLN5 A3A3 were performed in Tico buffer at pH 7.5 and 283 K.

Chemical shifts were previously assigned7 and obtained from data recorded on a Bruker Avance III operating at 700 and 800 MHz equipped with TCI cryoprobes. All samples contained 10% (v/v)

D2O and 0.001% (w/v) DSS as a reference. Data were processed analysed using NMRPipe63 (v11.7), CCPN64 (v2.4) and MATLAB (R2017a, Mathworks). Amide 1H and 15N chemical shifts were obtained

from two-dimensional 1H–15N SOFAST-HMQC experiments65 using an acquisition time of 50 ms in the direct dimension. The inter-scan delay was 50 ms. Cα chemical shifts were obtained from 3D

BEST-HNCA experiments recorded at 800 MHz with acquisition times of ~50 ms and inter-scan delays of 150 ms. C’ chemical shifts were obtained from BEST HNCO experiments recorded at 700 MHz

using acquisition times of ~50 ms and inter-scan delays of 200 ms. RNC samples were doped with 20 mM NiDO2A (Ni(ii) 1,4,7,10-tetraazacyclododecane-1,7-bis(acetic acid)) to enhance

sensitivity66. Cosine-squared window functions were used in processing the spectra. For PRE-NMR experiments, we used a cysteine-less construct with the C747V mutation and introduced six and

eight labelling sites in the isolated and ribosome-bound protein, respectively. Samples were reduced overnight at 277 K in Tico supplemented with 2 mM TCEP. TCEP was then removed by buffer

exchange into labelling buffer (50 mM HEPES, 12 mM MgCl2, 20 mM NH4Cl, 1 mM EDTA, pH 8.0) and subsequently labelled overnight at 277 K with 10× molar excess of MTSL. Following labelling,

excess MTSL was removed by buffer exchanging the sample back into Tico buffer for NMR. The same labelling protocol was used for isolated protein and RNC samples. To measure the PREs, we

recorded the signal intensities with MTSL in the paramagnetic and diamagnetic state. Direct measurements of relaxation rates proved not feasible for RNC samples due sensitivity limitations.

2D 1H–15N SOFAST-HMQC experiments65 were recorded at 800 MHz and 283 K using ~100 μM of protein or ~10 μM of RNC. Experiments were recorded with an acquisition time of 100 ms and 35 ms, in

the direct and indirect dimension, respectively. The inter-scan delay was 450 ms to allow for complete relaxation. To acquire the diamagnetic data, the sample was reduced with 2.5 mM (RNC)

or 100× molar excess (isolated) sodium ascorbate. Following complete reduction, the same HMQC experiment was recorded. To extract the PREs, spectral peaks were first fitted to a Lorentzian

shape in both the direct and indirect dimension using NMRPipe63. Errors were obtained from the spectral noise (RMSE). From the fitted peaks, intensity ratios of Ipara/Idia were calculated

and converted to PRE rates for Bayesian ensemble reweighting by numerically solving equation S34 (see Supplementary Notes 3–4) for Γ2. Sample integrity was monitored using interleaved 1H,15N

SORDID diffusion measurements as previously described7. PFG-NMR experiments were used to measure the diffusion coefficients and the _R_h of FLN5 variants. 1D 1H,15N-XTSE diffusion

measurements were recorded at 700 (FLN5, FLN5 Δ6) and 800 MHz (FLN5 A3A3). Eight to sixteen gradient strengths ranging linearly from 5% to 95% of the maximum gradient strength of 0.556 T m−1

were used. By measuring the signal intensity at each gradient strength, diffusion coefficients could be obtained by fitting the data to the Stejskal–Tanner equation67, which were converted

to _R_h using the Stokes–Einstein equation. RDCs for isolated FLN5 A3A3 were measured in Tico buffer at 283 K and pH 7.5 in a PEG/octanol mixture68. RDCs are reported as the splitting of the

isotropic splitting subtracted from the aligned splitting, corrected for the negative gyromagnetic ratio of 15N. RDCs were measured by preparing a solution containing 4.6% (w/w)

pentaethylene glycol monooctyl ether (C8E5), 1-octonal (molar ratio 1-octanol:C8E5 = 0.94) and 110 μM of protein. Alignment was confirmed by measuring the D2O deuterium splitting at 283 K

(17.6 Hz). All RDC NMR experiments were acquired on a Bruker Avance III HD 800 MHz spectrometer equipped with a TCI cryoprobe. A set of four different RDCs (1DNH, 1DCαCO, 1DCαHα and 2DHNCO)

was measured per sample (isotropic and anisotropic) using the 3D BEST HNCO (JCOH and JCC) or BEST-HNCOCA (JCAHA) experiments69,70,71. The one-bond 1H−15N coupling was determined by recording

two 15N-HSQC sub-spectra, in-phase (IP) and anti-phase (AP). For the measurement of the 1H-13CO coupling constants a BEST HNCO-JCOH experiment was used with an introduced DIPSAP filter.

Such _J_-mismatch compensated DIPSAP spin-state filter offers an attractive approach for accurate measurement of small spin–spin coupling constants72. For that, three separate experiments

were recorded with different filter lengths (2_τ_ = 1/_J_) for each anisotropic and isotropic media, where the sub-spectra associated to the separated spin states (two in phase and one

anti-phase) are combined using a linear relation _k_ (IP) + (_k_ − 1) (IP) ± (AP) with _k_ = 0.73, the theoretical optimized scaling factor. The spectra were recorded with 144 × 104 × 1,536

complex points in the 13C(_t_1)/15N (_t_2)/1H (_t_3) dimensions, respectively, and with the spectral widths set to 15,244 Hz (1H), 2,070 Hz (15N) and 1,510 Hz (13C) for the HNCO-JCOH. For

the HNCO-JCC and HNCOCA-JCAHA 256 × 200 × 1,536 complex points were acquired in the 13C(_t_1)/15N (_t_2)/1H (_t_3) dimensions, with spectral widths of 15,244 Hz (1H), 1,900 Hz (15N) and

1,214 Hz/5050 Hz (13C). The recycle delay was set to 200 ms, the acquisition time to 100 ms with 16 scans per increment, and the data was acquired in the non-uniform sampling format (2246

points for HNCO-JCOH and 7680 for the HNCO-JCC/HNCOCA-JCAHA experiments were sampled using the schedule generator from the web portal nus@HMS

(http://gwagner.med.harvard.edu/intranet/hmsIST/). The time domain data was converted into the NMRPipe63 format and reconstructed using the sparse multidimensional iterative

lineshape-enhanced method (SMILE)73. Coupling constants were obtained from line splitting in the 13C or 15N dimension obtained with CCPN analysis software64. 19F NMR experiments were

recorded on a 500 MHz Bruker Avance III spectrometer equipped with a TCI cryoprobe at 298 K (unless otherwise indicated) using a 350 ms acquisition time and 1.5–3 s recycle delay as

previously described6. We used an amber-suppression strategy to incorporate the unnatural amino acid tfmF, as previously described6. Multiple experiments were recorded in succession to

monitor sample integrity over time also as previously described6. Data were processed using NMRPipe63. Spectra were baseline corrected, peaks were fit to Lorentzian functions and errors of

the linewidths and integrals (that is, populations) were estimated using bootstrapping (200 iterations, calculating the standard error of the mean), or from the spectral noise for states

whose resonance was not detectable, in MATLAB6. 19F-translational diffusion experiments were performed as previously described6. Thermodynamic parameters of folding (Δ_H_, Δ_S_ and Δ_C_p)

were obtained from a nonlinear fit to a modified Gibbs–Helmholtz equation, assuming Δ_C_p remains constant across the experimental temperature range:

$${\rm{ln}}\left({K}_{{\rm{eq}},T}\right)=-\left(\frac{\Delta {H}_{{T}_{0}}+\Delta {C}_{{\rm{p}}}(T-{T}_{0})}{R}\right)\left(\frac{1}{T}\right)+\left(\frac{\Delta {S}_{{T}_{0}}+\Delta

{C}_{{\rm{p}}}{\rm{ln}}\left(\frac{T}{{T}_{0}}\right)}{R}\right)$$ (S1) _K_eq is the equilibrium constant, _T_ is the temperature in Kelvin and _T_0 is the standard temperature (298 K). We

also fitted the data to the linear van’t Hoff equation (assuming Δ_C_p = 0). $${\rm{ln}}\left({K}_{{\rm{eq}}}\right)=-\left(\frac{\Delta H}{R}\right)\left(\frac{1}{T}\right)+\frac{\Delta

S}{R}$$ (S2) The Scipy package with optimize.curve_fit function was used to perform the fits74 and errors were estimated as one s.d. from the diagonal elements of the parameter covariance

matrix. All parameters (Δ_H_, Δ_S_, Δ_C_p) generally showed strong correlations with each other (_r_ ≥ 0.8), and thus, their uncertainties correlate also. These parameter correlations are

expected75. The magnitudes of Δ_H_ and −_T_Δ_S_ are also expected to correlate because we study the temperature dependence of folding in a range where Δ_G_ of folding is close to 0. Folding

free energies were calculated from the experimental populations using Δ_G_ = −_RT_ln(_K_). The folding free energy of the FLN5+67 wild-type RNC, where no unfolded state is observable, was

estimated on the basis of two destabilizing mutants FLN5(V664A/F665A) and FLN5(V707A). The stability of these mutants was measured using 19F NMR on and off the ribosome. The FLN5+67

wild-type folding energy (Δ_G_N-U) was then calculated as the average from the V664A/F665A and V707A mutants using Δ_G_WT,+67 = Δ_G_mut,+67 − ΔΔ_G_mut-WT,iso, where ΔΔ_G_mut-WT,iso is the

experimentally measured destabilization in isolation. Given that at FLN5+34, both mutants show a weaker destabilization than in isolation, we reasoned that this estimate of the FLN5+67

wild-type folding free energy is its lower bound (most negative). 19F transverse relaxation rate (_R_2) measurements were recorded using a Hahn-echo sequence and acquired as pseudo-2D

experiments with relaxation delays of 0.1 to 200 ms. Data were processed using NMRPipe and analysed using MATLAB. Data were fit to lineshapes and _R_2 was obtained by fitting the integrals

to single exponential functions. We also orthogonally determined _R_2 from linewidth measurements of spectra acquired by 1D 19F pulse-acquire experiments, which showed excellent

correlations. The lineshape-derived _R_2 values also showed good correlation with previously determined rotational correlation times25 (_τ_C). We additionally determined the _S_2_τ_C of FLN5

in 60% glycerol at 278 K by measurements of triple quantum build-up and single quantum relaxation as previously described76,77. Thus, our _R_2 values can be used to determine rotational

correlation times (_τ_C,exp). The obtained _τ_C,exp was used to estimate the bound population as \(\frac{{\tau }_{{\rm{C}},\exp }-{\tau }_{{\rm{C,iso}}}}{{\tau }_{{\rm{C,bound}}}-\,{\tau

}_{{\rm{C,iso}}}}\), where _τ_C,iso is the rotational correlation time of the isolated protein25 (7.7 ns at 298 K) and _τ_C,bound is the expected rotational correlation time of the bound

state. _τ_C,bound is taken as the rotational correlation time of the ribosome itself (~3,000 ns at 298 K) for a fully rigid bound state. From the bound populations (_p_B), the resulting

change in the folding free energies of the intermediates was calculated as ΔΔ_G_I-U,RNC-iso = _RT_(ln(1 − _p_B)). We report the estimate for a fully rigid bound state in the main text

(\({S}_{{\rm{bound}}}^{2}=1.0\)) but note that even one order of magnitude more flexibility in the bound state (\({S}_{{\rm{bound}}}^{2}=0.1\)) only accounts for up to 1.1 ± 0.6 and 0.4 ± 

0.1 kcal mol−1 of stabilization for I1 and I2 on the ribosome at FLN5+47, respectively. These estimates still cannot account for the >4 kcal mol−1 of intermediate stabilization observed

on the ribosome6. All NMR experiments of RNCs are recorded and continuously interleaved with a series of 1D 1H/19 F spectra and 1H,15N/19F diffusion measurements6,7,61,78. These provide the

most sensitive means to assess changes in the sample, and when alterations in signal intensities or linewidths (that is, transverse relaxation rates), chemical shifts or translational

diffusion measurements of the nascent chain are observed, data acquisition is halted. Only data corresponding to intact RNCs are summed together and subjected to a final round of analysis.

Where signal-to-noise remains low, datasets from multiple samples are compared to ensure identical spectra, before summation together into a single NMR spectrum. Biochemical assays provide

an orthogonal means to assess nascent chain attachment to the ribosome. Identical samples incubated in parallel with NMR samples are analysed by SDS–PAGE (under low pH conditions61) and

detected with nascent-chain-specific antibodies. Ribosome-bound species migrate with an addition ~17-kDa band-shift relative to released nascent chains due to the presence of the tRNA

covalently linked to the nascent chain. Combined with time-resolved NMR measurements, these analyses confirm that the reported NMR resonances originate exclusively from intact RNCs. MASS

SPECTROMETRY FLN5 A3A3 was buffer exchanged into 100 mM (NH4)2CO3 at pH 6.8 (using formic acid for pH adjustment). Analyses were run on the Agilent 6510 QTOF LC–MS system at the UCL

Chemistry Mass Spectrometry Facility. Samples contained ~10–20 μM of protein and 10 μl were injected onto a liquid chromatography column (PLRP-S, 1,000 Å, 8 μm, 150 mm × 2.1 mm, maintained

at 60 °C). The liquid chromatography was run using water with 0.1% formic acid as mobile phase A and acetonitrile with 0.1% formic acid as phase B with a gradient elution and a flow rate of

0.3 ml min−1. ESI mass spectra were continuously acquired. The data were processed to zero charge mass spectra with the MassHunter software, utilizing the maximum entropy deconvolution

algorithm. SMALL-ANGLE X-RAY SCATTERING We measured SAXS of an isolated FLN5 A3A3 C747V sample in Tico buffer supplemented with 1% (w/v) glycerol. Data collection was performed at the

DIAMOND B21 beamline (UK)79 with a beam wavelength of 0.9408 Å, flux of 4 × 1012 photons s−1 and an EigerX 4 M (Dectris) detector distanced at 3.712 m from the sample. A capillary with a 1.5

 mm diameter kept at 283 K was used for data acquisition. We acquired SAXS data at multiple protein concentrations (5.5, 2.75, 1.38, 0.69, 0.34 and 0.17 mg ml−1) to assess whether the sample

exhibited signs of aggregation or interparticle interference. At 5 mg ml−1, we observed weak signs of interparticle interference in the low _q_ region of the scattering profile, which is

also reflected in the _R_g obtained by Guinier analysis (using the autorg tool from ATSAS80; Supplementary Table 1). Data were recorded as a series of frames, non-defective frames were

averaged, and buffer subtracted with PRIMUS80. Size-exclusion chromatography–SAXS (SEC–SAXS) experiments were additionally performed in Tico buffer with 1% (w/v) glycerol using a KW402.5

(Shodex) column to confirm the monodispersity of the sample. We chose the 2.75 mg ml−1 dataset as the final dataset to compare with our molecular dynamics simulations. This dataset exhibited

the highest signal to noise ratio and did not show signs of interparticle interference, and accordingly, the _R_g obtained from the 2.75 mg ml−1 dataset is consistent with the value

obtained from lower concentrations and the main SEC–SAXS peak (Supplementary Table 1). CIRCULAR DICHROISM SPECTROSCOPY The circular dichroism (CD) spectrum of isolated FLN5 A3A3 V747 was

acquired in 10 mM Na2HPO4 pH 7.5 at 283 K. A Chirascan-plus CD spectrometer (Applied Photophysics), a protein concentration of 44 μM and a cuvette with a 0.5 cm pathlength were used. HRAS

REFOLDING EXPERIMENTS HRAS refolding experiments were performed with the HRAS G-domain (residues 1–166). The protein was unfolded overnight at 298 K in Tico buffer with 2 mM

β-mercaptoethanol, 8 M urea and protein concentration of 15 μM. The protein was then refolded by rapidly diluting into Tico buffer (supplemented with 2 mM β-mercaptoethanol and 50 μM GDP) to

reach final urea and protein concentrations of 0.94 M and 1.76 μM, respectively, and allowed to incubate at 298 K for 24 h. For NMR analyses of refolded samples, we prepared 18 μM of

refolded protein with the same urea concentrations and dilutions. We assayed the functional/activity state of HRAS using GDP/GTP nucleotide exchange (‘activity’) assay81 with fluorescently

labelled GTP that exhibits higher fluorescence when bound to HRAS than free in solution (BODIPY FL GTP, ThermoFisher). 0.4 μM of HRAS, 0.01 μM of BODIPY GTP and 1 μM of SOScat (the catalytic

domain of Son of sevenless) were incubated at room temperature and the maximum (plateau) fluorescence recorded and normalized by the signal of the buffer (signal/noise ratio). SOScat was

produced as previously described82. Fluorescence measurements were performed using the CLARIOstar microplate reader (BMG Labtech) with excitation and emission wavelengths set to 488 and 514 

nm, respectively. The proteolytic stability of HRAS was assayed with thermolysin at a concentration of 0.05 mg ml−1 incubated with HRAS samples over the course of 5 h in vitro and 9 h in

rabbit reticulocyte lysate (RRL, TNT coupled reticulocyte lysate, Promega). Reactions were quenched with 23 mM EDTA. Timepoints were analysed by western blot analysis using a pan-RAS

polyclonal antibody (ThermoFisher, 1:1,000 dilution), utilizing an anti-rabbit IgG horseradish peroxidase-linked secondary antibody (Cell Signaling Technology, 1:1,000 dilution).

Densitometry analyses were performed with ImageJ83. For the RRL experiments, refolding reactions were performed in RRL for 24 h at 298 K and a final HRAS concentration of 1.6 μM followed by

pulse proteolysis and we quantified the relative band intensities (refolded/control) for each time point to account for increased background on the western blot during the proteolysis

reaction. MOLECULAR DYNAMICS SIMULATIONS We used the FLN5 A3A3 C747V sequence for all simulations. A reliability and reproducibility checklist is provided in Supplementary Table 8. GROMACS

(version 2021)84 was used for all all-atom molecular dynamics simulations in explicit solvent. We employed the Charmm36m force field in combination with the CHARMM TIP3P water model (C36m)

and the CHARMM TIP3P water model with an increased water hydrogen LJ well-depth (denoted here as C36m+W)85. We also used the a99sb-disp force field together the a99sb-disp TIP4P-D water

model86. Default protonation states were used in all cases. Starting from a random extended conformation, for all force field combinations the system was solvated in a dodecahedron box with

151,135 water molecules and 12 mM MgCl2 (resulting in 455,116 atoms and an initial box volume of 4,688 nm3). Systems were then energy minimized using the steepest-decent algorithm. For the

following dynamics simulations, we used the LINCS algorithm87 to constrain all bonds connected to hydrogen and a timestep of 2 fs using the leap-frog algorithm for integration. Nonbonded

interactions were calculated with a cut-off at 1.2 nm (including a switching function at 1.0 nm for van der Waals interactions) and the particle mesh Ewald (PME) method88 was used for

long-range electrostatic calculations. We then equilibrated the systems in two phases. First, we performed a 500 ps equilibration simulation in the NVT ensemble with position restraints on

all protein heavy atoms. The temperature was kept at 283 K using the velocity rescaling algorithm89 and a time constant of 0.1 ps. Next, we further equilibrated the systems for 500 ps in the

NPT ensemble at 283 K and a pressure of 1 bar with a compressibility of 4.5 × 10−5 bar−1 using the Berendsen barostat90. Following equilibration, we relaxed our initial structure for 100 ns

at 283 K without any position restraints using the Parrinello–Rahman algorithm91 and then picked five structures from this simulation for production simulations. We ran a total of 5× 2 μs

(with different initial coordinates and velocities) yielding a total of 10 μs of sampling per force field. For the C36m+W combination we ran an additional 5× 2 μs starting from 5 new

starting structures yielding 20 μs in total. We also generated a prior ensemble with a physics-based coarse-grained (C-alpha) model. We generated the C-alpha model template from the FLN5

crystal structure using SMOG 2.392, where all bonded terms have a global energy minimum at the values taken in the crystal structure93. Nonbonded van der Waals interactions were modelled

using a 10–12 Lennard-Jones potential with _σ_ and _λ_ parameters described in the M1 parameter determined by Tesei et al.94 (equation (S3)). We used the arithmetic mean of two residues to

determine _σ_ and _λ_. Electrostatic interactions were modelled using the Debye–Hückel theory with parameters described previously7. Interactions between Cα beads separated by less than four

residues were excluded. We ran initial simulations at a range of reduced temperatures to determine the effect on the average compactness and ran final simulations at a reduced temperature

of 1.247 (150 K in GROMACS) as we did not observe a significant increase in average _R_g beyond this temperature. Simulations were run for a total of 3 × 109 steps with GROMACS (v2018.3).

$${u}_{{\rm{LJ}}}=\mathop{\sum }\limits_{i}^{N}\lambda \left[{5\left(\frac{\sigma }{r}\right)}^{12}-6{\left(\frac{\sigma }{r}\right)}^{10}\right]$$ (S3) After simulations, the coarse-grained

ensemble was backmapped to an all-atom structure using PULCHRA (v3.06)95. RNC simulations were parameterized using the C36m+W force field/water model combination85,96. We modelled the

ribosome using the structure PDB 4YBB97 as a template, which we previously refined against a cryo-EM map containing an FLN5 RNC98. As in our previous work, we only retained ribosome atoms

around the nascent chain exit tunnel and accessible surface outside the vestibule7. The FLN6 linker and SecM sequence were initially modelled using a cryo-EM map of a FLN5+47 RNC

(Mitropoulou et al., manuscript in preparation). The rest of the nascent chain (MHHHHHAS N-terminal tag and FLN5) was then built using PyMol version 2.3 (The PyMol Molecular Graphics System,

Schrödinger) and we generated a random initial starting structure with a short simulation using a structure-based force field, SMOG2.392, without native contacts. The FLN5+31 A3A3 RNC

(containing the C747V mutation) complex was then centred in a dodecahedral box, solvated using 1,030,527 water molecules and neutralized with 706 Mg2+ ions, resulting in a final system size

of 3,163,127 atoms. The initial box volume was 32,117 nm3. The large box size was necessary to accommodate the highly expanded unfolded state. We then used the same cut-offs and simulation

methods as for the isolated protein. We initially also ran a 500 ps equilibration simulation in the NVT ensemble using position restraints on all heavy atoms using a force constant of 1,000 

kJ mol−1 nm2 in along the _x_, _y_ and _z_ axes. We used a temperature of 283 K, which was held constant using the velocity rescaling algorithm89 and a time constant of 0.1 ps. Then, we ran

a 500 ps equilibration simulation in the NPT ensemble at 283 K using the same position restraints. The pressure was kept at 1 bar with a compressibility of 4.5 × 10−5 bar−1 using the

Berendsen barostat90. The position restraints for all nascent chain atoms (except the terminal residue at the PTC in the ribosome) were then removed, while the ribosome atoms kept being

position restrained. In this setup, we ran a 1 ns equilibration simulation at 283 K and 1 bar, using the Parrinello–Rahman algorithm91. All production simulations were performed using

position restraints for the ribosome atoms and C-terminal nascent chain residue at the PTC. Using the equilibrated configuration, we then ran two simulations of ~100 ns to picked ten

starting structures for production simulations. Then, ten production simulations of 1.5 μs each (15 μs) were initiated from these different starting structures using random initial

velocities. Before the production simulation, each structure was re-equilibrated at 283 K and 1 bar with a 500 ps NVT and 500 ps NPT simulation. Lastly, to compare our C36m+W simulations

with a model that only considers steric exclusion as a nonbonded interaction, we also ran simulations of a simple all-atom model, based on a structure-based model template92. We used the

FLN5 crystal structure to define the energy minima of all bond and dihedral angles and removed all native contacts. Simulations of isolated and ribosome-bound FLN5 A3A3 were run for 1 × 109

steps and 100,000 frames were harvested for analysis. This ensemble was used to compare the expansion of the ensemble, ribosome interactions and conformational entropy with the C36m+W

simulations. CALCULATION OF PRES The transverse PRE rates of backbone amide groups, _Γ__2_, were back-calculated from the ensembles using the Solomon–Bloembergen equation99,100 $${\varGamma

}_{2}=\frac{1}{15}{\left(\frac{{\mu }_{0}}{4\pi }\right)}^{2}{\gamma }_{{\rm{H}}}^{2}\,{g}_{{\rm{e}}}^{2}{\mu }_{{\rm{B}}}^{2}S(S-1)[4J(0)+3J({\omega }_{{\rm{H}}})]$$ (S4) where _μ_0 is the

permeability of space, _γ_H is the gyromagnetic ratio of the proton, _g_e is the electron g-factor, _γ_B is the Bohr magneton, _S_ is the proton nuclear spin and _J_(_ω_0) is the generalized

spectral density function. For flexible spin labels attached via rotatable bonds the spectral density can be expressed as in equation (S5)101. $$J({\omega }_{{\rm{H}}})=\langle

{r}^{-6}\rangle \left[\frac{{S}^{2}{\tau }_{{\rm{c}}}}{1+{({\omega }_{{\rm{H}}}{\tau }_{{\rm{c}}})}^{2}}+\frac{(1-{S}^{2}){\tau }_{{\rm{t}}}}{1+{({\omega }_{{\rm{H}}}{\tau

}_{{\rm{t}}})}^{2}}\right]$$ (S5) where \(\langle {r}^{-6}\rangle \) is the average of the electron–hydrogen distance (_r_) distribution, _S_2 is the generalized order parameter for the

electron–hydrogen interaction vector, _τ_C is the correlation time defined in terms of the rotational correlation time of the protein (_τ__r_) and the electron spin relaxation time (_τ__s_):

$${\tau }_{c}={\left({\tau }_{r}^{-1}+{\tau }_{s}^{-1}\right)}^{-1}$$ (S6) _τ__t_ is the total correlation time defined as: $${\tau }_{{\rm{t}}}={\left({\tau }_{r}^{-1}+{\tau

}_{s}^{-1}+{\tau }_{{\rm{i}}}^{-1}\right)}^{-1}$$ (S7) _τ__i_ is the internal correlation time of the spin label. Since for nitroxide labels electron spin relaxation occurs on a much slower

timescale than rotational tumbling101,102, _τ_C can be approximated to _τ__r_ such that expression for _τ__t_ simplifies to $${\tau }_{{\rm{t}}}={\left({\tau }_{{\rm{C}}}^{-1}+{\tau

}_{i}^{-1}\right)}^{-1}$$ (S8) Given that _τ__C_ is not known a priori, we iteratively scanned _τ__C_ values in the range of 1 to 15 ns to find a value for which optimal agreement with the

experimental data is achieved (as judged by the reduced _χ_2)94,103. The spin label correlation time104, _τ__i_ was set to 500 ps, in agreement with molecular dynamics simulations105 and

electron spin resonance measurement106. The generalized order parameter _S_2 for the electron–hydrogen interaction vector can be decomposed into its radial and angular components107:

$${S}_{{\rm{PRE}}}^{2}\approx {S}_{{\rm{PRE}},{\rm{angular}}}^{2}{S}_{{\rm{PRE}},{\rm{radial}}}^{2}$$ (S9) where the individual components are defined as

$${S}_{{\rm{PRE,angular}}}^{2}=\frac{4\pi }{5}\mathop{\sum }\limits_{m=-2}^{2}{\left|\langle {Y}_{2}^{m}({\varOmega }^{{\rm{mol}}})\rangle \right|}^{2}$$ (S10)

$${S}_{{\rm{PRE}},{\rm{radial}}}^{2}=\langle {r}^{-6}{\rangle }^{-1}\langle {r}^{-3}{\rangle }^{2}$$ (S11) and \({Y}_{2}^{m}\) are the second order spherical harmonics and _Ω_mol are the

Euler angles in the frame. A weighted ensemble average of _S_2 can be calculated by taking a weighted ensemble average of the individual radial and angular components. A previously published

rotamer library containing 216 MTSL rotamers108 was used to explicitly model the flexibility of the spin label, similar to other existing methods109,110. The rotamer library was aligned to

all employed labelling sites for each conformer using the backbone atoms of the labelling site and Cys-MTSL moiety. Clashing rotamers were discarded, where a steric clash between the rotamer

and the protein was defined using a 2.5 Å cut-off distance. Only backbone and Cβ atoms were considered for the protein, assuming sidechains can rearrange to accommodate the MTSL rotamer111.

For MTSL, only the sidechain was included (heavy atoms beyond the Cβ atom). Protein frames for which at least one labelling position cannot sterically allow any MTSL rotamers were

discarded. The rotamer library was used to calculate a weighted ensemble-averaged _Γ_2 over the rotamer ensemble for each protein conformer in the protein ensemble using equations (S3−S11).

The protein ensemble average can then be calculated by averaging _Γ_2 over the ensemble. PRE intensity ratios were then calculated from the ensemble-averaged PRE rate, \(\langle {\varGamma

}_{2}\rangle \), using $$\frac{{{\rm{I}}}_{{\rm{p}}{\rm{a}}{\rm{r}}{\rm{a}}}}{{{\rm{I}}}_{{\rm{d}}{\rm{i}}{\rm{a}}}}=\frac{{R}_{2}{{\rm{e}}}^{-2\Delta \langle {\varGamma }_{2}\rangle

}}{{R}_{2}+\langle {\varGamma }_{2}\rangle }\times \frac{{R}_{2,{\rm{M}}{\rm{Q}}}}{{R}_{2,{\rm{M}}{\rm{Q}}}+\langle {\varGamma }_{2}\rangle }$$ (S12) where _R_2 is the linewidth in the

proton dimension (residue-specific), _R_2,MQ is the linewidth in the nitrogen dimension (multiple-quantum term) and _Δ_ is the delay time in the HMQC experiment (5.43 ms). See Supplementary

Note 3 for additional details. For RNCs, we considered that that ribosome tethering may increase the correlation time of the electron–amide interaction vector due to restricted molecular

tumbling near the exit tunnel. We therefore calculated an order parameter, \({S}_{{\rm{NC}}}^{2}\), which quantifies the motion of the electron-interaction vector over the entire nascent

chain conformer ensemble (\({S}_{{\rm{NC}}}^{2}\) is distinct from the order parameter _S_2 that quantifies the motion of the MTSL rotamer library attached to a labelling site for a specific

protein conformer; equation (S9)). _S_2 is given by $${S}_{{\rm{NC}}}^{2}\approx {S}_{{\rm{NC,angular}}}^{2}{S}_{{\rm{NC,radial}}}^{2}$$ (S13) where \({S}_{{\rm{NC}},{\rm{angular}}}^{2}\)

and \({S}_{{\rm{NC}},{\rm{radial}}}^{2}\) are given by $${S}_{{\rm{PRE}},{\rm{angular}}}^{2}=\frac{4\pi }{5}\mathop{\sum }\limits_{m=-2}^{2}{| \langle {Y}_{2}^{m}({\varOmega

}^{{\rm{mol}}})\rangle | }^{2}$$ (S14) $${S}_{{\rm{PRE}},{\rm{radial}}}^{2}=\langle {r}^{-6}{\rangle }^{-1}\langle {r}^{-3}{\rangle }^{2}$$ (S15) and \({Y}_{2}^{{\rm{m}}}\) are the second

order spherical harmonics and _Ω_mol are the Euler angles in the frame. We approximated the position of the free electron with the Cα atom of the labelling site in this case. A

\({S}_{{\rm{NC}}}^{2}\) value of 0 indicates that the vector tumbles completely independent of the ribosome and that the correlation time of the electron–amide vector is the same as for the

isolated protein, _τ_C,iso. A \({S}_{{\rm{NC}}}^{2}\) value of 1 means that the vector tumbles with the same rotational correlation time as the ribosome (_τ_r,70S = 3.3 μs per cP, as

determined by fluorescence depolarization112, and _τ_r,70S = 4.3 μs at 283 K in H2O). The effective correlation time, _τ_C,eff, of each amide-electron vector is given by $${\tau

}_{{\rm{C,eff}}}\,={S}_{{\rm{NC}}}^{2}{\tau }_{{\rm{r,70S}}}+(1-{S}_{{\rm{NC}}}^{2}){\tau }_{{\rm{C,iso}}}$$ (S16) We used a value of 3 ns for _τ_C,iso, which was the optimal value

determined for isolated FLN5 A3A3. Generally, _τ__C_ (equation (S6)) is approximated as _τ_C ≈ _τ_r because the electron spin relaxation time, _τ_s, occurs on a much slower timescale. In

fact, measurements of the spin relaxation time of nitroxides have been measured to be on a timescale from hundreds of nanoseconds to several microseconds113,114,115. The calculated values of

_τ_C,eff are predominantly below 100 ns except for labelling sites C744, uL23 G90C and uL24 N53C, where values of up to ~250 ns are observed (Supplementary Tables 5 and 6). Thus, we still

expect _τ_C to be dominated by _τ_r and make use of the _τ_C ≈ _τ_ approximation. Finally, reference PRE profiles for a fully extended peptide were calculated from a linear polyalanine chain

using a _τ_C of 5 ns and _R_2,H_/R_2,MQ of 100 Hz. BAYESIAN INFERENCE REWEIGHTING We performed ensemble refinement by reweighting the molecular dynamics-derived ensembles against the

experimentally deduced _Γ_2 rates using the Bayesian Inference of Ensembles (BioEn) software and method described in the corresponding paper116,117. These calculations were performed using

in-house scripts of the software with the modification to incorporate upper and lower bound restraints in addition to regular restraints with gaussian errors. To this end, these inequality

restraints were treated as normal gaussian restraints but subjected to a conditional statement. Lower bound restraints (_Γ_2 > 64.5 s−1 for isolated FLN5 A3A3; _Γ_2 > 96.0 s−1 for the

RNCs) were applied only if the back-calculated _Γ_2 was below the lower bound value. Similarly, upper bound restraints (_Γ_2 < 2.2 s−1 for isolated FLN5 A3A3; _Γ_2 < 3.7 s−1 for the

RNCs) were applied only if the back-calculated average was above the upper bound. This effectively allows the back-calculated value to vary freely above the lower bound and below the upper

bound but imposes a penalty if the inequality condition is not met. The errors of the lower and upper bound values were taken as the combined relative error of that datapoint (that is, the

intensity ratio). As described by Köfinger et al.117, the reweighting optimization problem can be efficiently solved by minimizing the negative log-posterior function (_L_). $$L=\theta

{S}_{{\rm{KL}}}+\mathop{\sum }\limits_{i=1}^{M}\frac{{\left({\sum }_{\alpha =1}^{N}{w}_{\alpha }{y}_{i}^{\alpha }-{Y}_{i}\right)}^{2}}{2{\sigma }_{i}^{2}}$$ (S17) _θ_ expresses the

confidence in the initial ensemble, _N_ is the ensemble size, _M_ is the number of experimental restraints, _w__α_ is the vector of weights for the conformers in the ensemble,

\({y}_{i}^{\alpha }\) is the back-calculated experimental value _i_, _Y__i_ is the experimental restraint _i_, _σ__i_ is the uncertainty of experimental restraint _i_, and _S_KL is the

Kullback–Leibler divergence defined as $${S}_{{\rm{KL}}}=\mathop{\sum }\limits_{\alpha =1}^{N}{w}_{\alpha }{\rm{ln}}\frac{{w}_{\alpha }}{{w}_{\alpha }^{0}}$$ (S18) \({w}_{\alpha }^{0}\) is

the vector of initial weights (which were uniform). We used the log-weights method to minimize the negative log-posterior117 and performed reweighting calculations for a range of _θ_ values,

as the optimal value of _θ_ cannot be known a priori. Therefore, we conduct L-curve analysis117,118 by plotting _S_KL (entropy) on the _x_ axis and the goodness of fit, quantified by the

reduced _χ_2 value, on the _y_ axis. The reduced _χ_2 was calculated against the experimental intensity ratios (Ipara/Idia). This is an effective method to prevent overfitting and

introducing a minimal amount of bias into the prior ensemble117,119. After reweighting, we also calculated the effective fraction of frames contributing to the ensemble average119 as an

indication of the extent of fitting. $${N}_{{\rm{eff}}}=\exp (-{S}_{{\rm{KL}}})$$ (S19) For RNCs, we used the same approach with an additional modification. Since the PRE depends on _τ_C,eff

and \({S}_{{\rm{NC}}}^{2}\) which are a function of the weights of individual structures in the ensemble, this consequently leads to changes in _τ_C,eff and \({S}_{{\rm{NC}}}^{2}\) when

reweighting is performed. Therefore, the conformer-specific PRE values that were used for reweighting are not the same anymore after reweighting. To account for this, we performed 20

iterative rounds of reweighting where each additional round receives input weights and _τ_C,eff from the previous round. We found that this leads to convergence of the weights and

conformer-specific PREs. We found that for the ribosomal labelling sites, uL23 G90C and uL24 N53C, the reweighting results are sensitive to the specific ribosome structure used to fit the

MTSL rotamer library to, since small variations in the local structure of the labelling site can lead to different rotamer distributions. We tested two different rotamer distributions for

the ribosomal labelling sites (Extended Data Fig. 5a), finding that one of them (referred to as R2) gives better agreement with the intermolecular PRE data after reweighting and fits better

into the expected density or MTSL rotamers when rotamers are fitted to ten high-resolution ribosome structures (Extended Data Fig. 5a). The R2 rotamer distribution is more representative of

the expected variation from structural changes in the labelling sites and was therefore used for our final reweighting calculations. CALCULATION OF RDCS, _R_ H AND CHEMICAL SHIFTS FROM

MOLECULAR DYNAMICS SIMULATIONS To back-calculate the _R_h from static structures we used an approximate relationship between _R_g and _R_h values120, the latter being calculated from the

programme HYDROPRO121. Thus, we calculated the _R_g from Cα atoms using MDAnalysis122 and then converted it to _R_h using $${R}_{{\rm{h}}}=\frac{{R}_{{\rm{g}}}}{\frac{{\alpha

}_{1}\left({R}_{{\rm{g}}}-{\alpha }_{2}{N}^{0.33}\right)}{{N}^{0.60}-{N}^{0.33}}+{\alpha }_{3}}$$ (S20) _N_ is the number of amino acids, _α_1 takes a value of 0.216 Å−1, _α_2 takes a value

of 4.06 Å, and _α_3 has a value of 0.821. The estimated value of _R_h (relative to the HYDROPRO calculation) has an average relative uncertainty120 of 3%. HYDROPRO itself has a relative

uncertainty of ±4% with respect to experimental values121. Therefore, we treat the back-calculated ensemble-average _R_h with a total relative uncertainty of ±5%. The ensemble average was

calculated as previously described by Ahmed et al. for back-calculation of PFG-NMR derived values123 of _R_h $$\langle {R}_{{\rm{h}}}\rangle ={\rm{ln}}{\left(\langle \exp

\left(-{R}_{{\rm{h}}}^{-1}\right)\rangle \right)}^{-1}.$$ (S21) Chemical shifts were calculated using the SHIFTX2 software124 and RDCs were calculated using the global alignment prediction

method implemented in PALES125. We then scaled the magnitude (that is, the extent of alignment) of the calculated RDCs by a global factor to optimize the Q-factor for each ensemble.

CALCULATION OF SAXS PROFILES FROM MOLECULAR DYNAMICS SIMULATIONS We used Pepsi-SAXS126 to compute the theoretical scattering profiles of each conformer in the molecular dynamics ensembles.

We treated the contrast of the hydration layer _(δ_p) and the effective atomic radius (_r_0) as global parameters and used values of 3.34 e− nm−3 and 1.025 × _r_m (_r_m = average atomic

radius of the protein) in line with previous work that showed these parameters to well suited for flexible proteins127. The constant background and scale factor were also fitted globally

using least-squares regression103,127. The goodness of fit was assessed using the reduced _χ_2 metric, where _n_ is the number of datapoints, _q_ is the scattering angle,

\({I}_{q}^{{\rm{calc}}}\) and \({I}_{{q}}^{\text{exp}}\) are the calculated and experimental scattering intensities, respectively, and _σ__q_ is the experimental error: $${\chi

}_{r}^{2}=\frac{1}{n}\mathop{\sum }\limits_{{q}}^{n}\frac{{({I}_{{q}}^{\text{calc}}-{I}_{{q}}^{\text{exp}})}^{2}}{{\sigma }_{{q}}^{2}}$$ (S22) STRUCTURAL ANALYSIS The Python package

MDAnalysis122 and MDTraj128 were used for general analysis of the ensembles involving atomic coordinates. For native contact analysis, we calculated the fraction of native contacts (relative

to the native FLN5 crystal structure) as129 $$Q(X)=\frac{1}{N}\sum _{ij}\frac{1}{1+{{\rm{e}}}^{\left(\beta \left({r}_{i,j}-\lambda {r}_{i,j}^{0}\right)\right)}}$$ (S23) where _r__i_,_j_ and

\({r}_{i,j}^{0}\) are the distances between atoms _i_ and _j_ in frame _X_ and the template structure, respectively, _β_ modulates the smoothness of the switching function (default value 5 

Å−1 used) and _λ_ is a factor allowing for fluctuations of the contact distance (default value 1.8 used). Asphericity was calculated using MDAnalysis122 as defined by Dima and Thirumalai130:

$$\Delta =\frac{3}{2}\frac{{\sum }_{n=1}^{3}{\left({\lambda }_{i}-\bar{\lambda }\right)}^{2}}{tr{T}^{2}}$$ (S24) \(\bar{\lambda }\) represents the mean eigenvalue obtained from the inertia

tensor \(\bar{\lambda }=\,\frac{{\rm{trT}}}{3}\). For the intrachain contact analysis, we defined contacts between Cα–Cα distances of less than 10 Å. The contact features qualitatively were

unchanged when using lower cut-off values or when calculating contacts between all heavy atoms. Secondary structure populations were calculated using DSSP131 implemented in MDTraj. The SASA

was calculated using GROMACS84. Clustering was also performed in GROMACS using the GROMOS algorithm132 and Cα RMSD cut-offs in the range of 1.2–1.8 nm. ERROR ANALYSIS FROM ENSEMBLES Errors

from the molecular dynamics ensembles were estimated using a block analysis of the full concatenated ensembles (composed of multiple statistically independent simulations). We performed

block analysis for the concatenated ensembles to verify that the estimate of the standard error of the mean (s.e.m.) plateaus/fluctuates at block sizes larger than blocks corresponding to

the individual trajectories. The final block size was chosen either in the plateau region of block analysis plots or corresponding to the blocks of the statistically independent simulation

(10 independent simulations were run for the isolated and RNC systems with the C36m+W force field, and thus 10 blocks were chosen for block analysis and error estimation). The error after

reweighting with PRE-NMR data was calculated the same way using a weighted standard error, where blocks are weighted according to the weights obtained from reweighting with PRE-NMR data.

Exemplar block analysis plots are shown in Supplementary Fig. 8. ENERGETIC ANALYSES FROM STRUCTURAL ENSEMBLES The conformational entropy was calculated as defined by Baxa et al.133. Proline,

glycine and alanine entropies were calculated from the backbone probability distribution _P__i_(_Φ_,_Ψ_). Residues with a maximum of two sidechain torsion angles, _X__n_, the entropy was

calculated from the probability distribution _P__i_(_Φ_,_Ψ_,_X__1_,_X__2_), while residues with more sidechain torsion angles was calculated from the sum of entropies obtained using the

_P__i_(_Φ_,_Ψ_,_X__1_), and _P__i_(_X__n_), after subtraction of the entropy obtained from _P__i_(_X__1_). Entropies were calculated from probability distributions using

\(S={-k}_{{\rm{B}}}{\sum }_{i=1}^{n}{P}_{i}{\rm{ln}}({P}_{i})\). We used a block analysis from the pooled ensembles (i.e., all individual trajectories concatenated together) to check that

the entropy difference between on and off the ribosome is robust with respect to sampling by calculating entropy changes with increasing amounts of total sampling (from the 15 and 20μs of

concatenated sampling for the RNC and isolated protein, respectively). The errors were then also estimated from the same sampling/block sizes up to 7.5 μs of molecular dynamics sampling.

This is because the estimate of entropy differences trend increases up to total sampling times of 7.5 μs (Extended Data Fig. 6g). The energetic contributions due to changes in solvation were

estimated based on empirical relationships between changes in the polar and apolar accessible surface area75,134 (ΔASApolar and ΔASAapolar). The apolar and polar surface area of the protein

were defined based on the atomic partial charges in the C36m force field85. Atoms with an absolute charge of less than or equal to 0.3 were defined as apolar. The change in heat capacity of

hydration is related to these quantities by $$\Delta C=\Delta {C}_{{\rm{apolar}}}+\Delta {C}_{{\rm{polar}}}=\alpha \times \Delta {{\rm{ASA}}}_{{\rm{apolar}}}+\beta \times \Delta

{{\rm{ASA}}}_{{\rm{polar}}}$$ (S25) where _α_ and _β_ are 0.34 ± 0.11 and −0.12 ± 0.12 cal mol−1 K−1 Å−2, respectively. We obtained these values as an average and standard deviation of

parameters previously reported in the literature as summarized in ref. 135 to account for the uncertainty of the parameters in addition to the uncertainty coming from conformational sampling

in our simulations. The enthalpy change due to solvation is then obtained from75 $$\Delta {H}_{{\rm{solv}}}\left(333\,{\rm{K}}\right)=\gamma \times \Delta {{\rm{ASA}}}_{apolar}+\delta

\times \Delta {{\rm{ASA}}}_{polar}$$ (S26) $$\Delta {H}_{{\rm{solv}}}\left(T\right)=\Delta {H}_{{\rm{solv}}}\left(333\,{\rm{K}}\right)+\Delta C(T-333\,{\rm{K}})$$ (S27) _T_ is the

temperature and _γ_ and _δ_ constants taking on values of −8.44 and 31.4 cal mol−1 Å−2, respectively. While we are not aware of alternative parameter sets for the solvation enthalpy

(equation (S26)) in the literature, we treated these parameters with a relative uncertainty of 50% to show that even with such high levels of uncertainty our conclusions are not affected.

Finally, the solvation entropy and change in free energy are then calculated using $$\Delta {S}_{333{\rm{K}},{\rm{solv}}}=\Delta

{C}_{{\rm{apolar}}}\,{\rm{ln}}\left(\frac{T}{{T}_{{\rm{apolar}}}}\right)-\Delta {C}_{{\rm{polar}}}\,{\rm{ln}}\left(\frac{T}{{T}_{{\rm{polar}}}}\right)$$ (S28) $$\Delta

{G}_{{\rm{solv}}}=\Delta {H}_{{\rm{solv}}}-T\Delta {S}_{{\rm{solv}}}$$ (S29) where _T_apolar and _T_polar are the temperatures at which Δ_S_solv,apolar and Δ_S_solv,polar are 0 (385 K and

335 K, respectively). Our previous work indicated ribosome solvation changes during coTF is not a major factor in coTF thermodynamics (see Supplementary Note 9), we estimated the above

quantities using surface areas calculated excluding the ribosome. We regard these absolute quantities as an estimated upper bound for _ΔG_solv because it is likely that folding intermediates

and the native state also interact with the ribosome6, thus effectively cancelling out any reduction in SASA of the unfolded state due to ribosome interactions. However, in the following

section we describe an alternative, more direct approach for the solvation entropy that does not rely on this assumption. CALCULATION OF SOLVATION ENTROPY CHANGES USING THE 2PT METHOD The

water and solvation entropy changes were also assessed more directly from molecular dynamics simulations using the two-phase thermodynamic (2PT) method136 implemented in the DoSPT code

(https://dospt.org/index.php/DoSPT)137. For these calculations, we chose five snapshots from our isolated FLN5 A3A3 V747 simulations detailed above (that is, with different initial protein

conformations and solvent configuration) and use these to initiate short molecular dynamics simulations for entropy calculations. We first re-equilibrated the boxes for 10 ns at the target

temperature in the NPT ensemble at 1 bar using the velocity rescaling algorithm89 and the Parrinello–Rahman algorithm91 as detailed above and the velocity Verlet integration algorithm (md-vv

in GROMACS84). Production simulations were then run in the NVT ensemble at 283 K and 298 K (to assess the effect of temperature on the water entropy calculations) for 20 ps using the md-vv

integrator and saving coordinates and velocities for analysis every 4 fs. Control simulations of pure TIP3P (CHARMM TIP3P) water in a cubic box with a box vector length of 5 nm, resulting in

4,055 water molecules. Five independent simulations were performed by first energy minimizing the system using the steepest-decent algorithm. Then, using a 2 fs timestep and

thermostat/barostat settings as for the protein and the md-vv integrator we equilibrated the water box first in the NVT ensemble for 1 ns, followed by 1 ns in the NPT ensemble using the

Berendson barostat90. The water box was then further equilibrated in the NVT ensemble for 1 ns prior to the production simulation in the NVT ensemble for 20 ps, saving coordinates and

velocities every 4 fs. These production simulations were also performed at 283 K and 298 K and then used to calculate the molar entropies of pure water at these temperatures with DoSPT. For

water entropy calculations in the protein system, we first analysed the radial distribution function water surrounding the protein molecule using our 15 μs and 20 μs molecular dynamics

ensembles of the isolated protein and RNC and the GROMACS rdf functionality84 to identify the region of the first two hydration shells that show significantly reduced water dynamics. Using

this analysis, we chose a distance cut-off of 3.5 Å between the protein and water centre of mass to define the hydration layer around the protein. With this criterion we then calculated the

probability distribution and average number of water molecules in the hydration layer to assess the difference in solvation on and off the ribosome. Water molecules that remain within a

defined distance range from the protein during the entire 20 ps production simulation were then selected to calculate the average molar entropy per molecule of water in different

environments with DoSPT. The accessible volume for this subsystem was estimated by using the average volume occupied per water molecule in a pure water box under identical conditions

multiplied by the number of molecules. To obtain the change in solvation entropy (difference between the RNC and isolated system, Δ_S_solv,RNC-iso), we used $$\Delta

{S}_{{\rm{solv,RNC}}-{\rm{iso}}}={N}_{{\rm{diff}}}\Delta {S}_{{\rm{solv,water}}}$$ (S30) where _N_diff is the average difference in the number of water molecules in the hydration layer

(RNC-iso) and Δ_S_solv,water is the entropy difference between water molecules in the hydration layer (0–3.5 Å from the protein) and water molecules in bulk solution (defined here as 36–46 Å

from the protein). REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY Data are

available as source data with the figures. The NMR assignment of FLN5 A3A3 has been previously deposited in the Biological Magnetic Resonance Data Bank (BMRB) under the entry code 51023. The

structural ensembles of the unfolded states have been deposited on Zenodo (https://doi.org/10.5281/zenodo.11618750 (ref. 138)). This study made use of the following public datasets

deposited in the protein databank (PDB, https://www.rcsb.org/): 4YBB, 6PJ6, 6XZ7, 7K00, 7LVK, 7N1P, 7O1A, 7PJS, 7Z20, 7ZP8, 1QFH, 1TIT and 4Q21. Source data are provided with this paper.

CODE AVAILABILITY Python scripts used to calculate PRE-NMR data from the ensembles and to refine the ensembles by reweighting are available on Github

(https://github.com/julian-streit/PREreweighting). NMR pulse sequences are available on Github (https://github.com/chriswaudby/pp). Codes used to fit the 19F NMR spectra are available on

Github (https://github.com/shschan/NMR-fit). CHANGE HISTORY * _ 15 AUGUST 2024 In the Supplementary Information originally published online, the Supplementary references were inadvertently

omitted. The Supplementary Information file has now been updated. _ REFERENCES * Cassaignau, A. M. E., Cabrita, L. D. & Christodoulou, J. How does the ribosome fold the proteome? _Annu.

Rev. Biochem._ 89, 389–415 (2020). Article  CAS  PubMed  Google Scholar  * Ahn, M. et al. Modulating co-translational protein folding by rational design and ribosome engineering. _Nat.

Commun._ 13, 4243 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Holtkamp, W. et al. Cotranslational protein folding on the ribosome monitored in real time. _Science_

350, 1104–1107 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Plessa, E. et al. Nascent chains can form co-translational folding intermediates that promote post-translational folding

outcomes in a disease-causing protein. _Nat. Commun._ 12, 6447 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Kaiser, C. M., Goldman, D. H., Chodera, J. D., Tinoco, I.

Jr. & Bustamante, C. The ribosome modulates nascent protein folding. _Science_ 334, 1723–1727 (2011). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Chan, S. H. S. et al.

The ribosome stabilizes partially folded intermediates of a nascent multi-domain protein. _Nat. Chem._ 14, 1165–1173 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Cassaignau, A. M. E. et al. Interactions between nascent proteins and the ribosome surface inhibit co-translational folding. _Nat. Chem._ 13, 1214–1220 (2021). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Jensen, M. K., Samelson, A. J., Steward, A., Clarke, J. & Marqusee, S. The folding and unfolding behavior of ribonuclease H on the ribosome. _J. Biol. Chem._

295, 11410–11417 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Samelson, A. J., Jensen, M. K., Soto, R. A., Cate, J. H. & Marqusee, S. Quantitative determination of

ribosome nascent chain stability. _Proc. Natl Acad. Sci. USA_ 113, 13402–13407 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Liu, K., Rehfus, J. E., Mattson, E. &

Kaiser, C. M. The ribosome destabilizes native and non-native structures in a nascent multidomain protein. _Protein Sci._ 26, 1439–1451 (2017). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Cabrita, L. D. et al. A structural ensemble of a ribosome-nascent chain complex during cotranslational protein folding. _Nat. Struct. Mol. Biol._ 23, 278–285 (2016). Article  CAS

  PubMed  PubMed Central  Google Scholar  * Deckert, A. et al. Common sequence motifs of nascent chains engage the ribosome surface and trigger factor. _Proc. Natl Acad. Sci. USA_ 118,

e2103015118 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Knight, A. M. et al. Electrostatic effect of the ribosomal surface on nascent polypeptide dynamics. _ACS Chem.

Biol._ 8, 1195–1204 (2013). Article  CAS  PubMed  Google Scholar  * Frydman, J., Erdjument-Bromage, H., Tempst, P. & Hartl, F. U. Co-translational domain folding as the structural basis

for the rapid de novo folding of firefly luciferase. _Nat. Struct. Biol._ 6, 697–705 (1999). Article  CAS  PubMed  Google Scholar  * Evans, M. S., Sander, I. M. & Clark, P. L.

Cotranslational folding promotes β-helix formation and avoids aggregation in vivo. _J. Mol. Biol._ 383, 683–692 (2008). Article  CAS  PubMed  PubMed Central  Google Scholar  * Samelson, A.

J. et al. Kinetic and structural comparison of a protein’s cotranslational folding and refolding pathways. _Sci. Adv._ 4, eaas9098 (2018). Article  ADS  PubMed  PubMed Central  Google

Scholar  * Liutkute, M., Maiti, M., Samatova, E., Enderlein, J. & Rodnina, M. Gradual compaction of the nascent peptide during cotranslational folding on the ribosome. _eLife_ 9, e60895

(2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * To, P., Whitehead, B., Tarbox, H. E. & Fried, S. D. Nonrefoldability is pervasive across the _E. coli p_roteome. _J. Am.

Chem. Soc._ 143, 11435–11448 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Braselmann, E., Chaney, J. L. & Clark, P. L. Folding the proteome. _Trends Biochem. Sci._ 38,

337–344 (2013). Article  CAS  PubMed  PubMed Central  Google Scholar  * Shortle, D. & Ackerman, M. S. Persistence of native-like topology in a denatured protein in 8 M urea. _Science_

293, 487–489 (2001). Article  CAS  PubMed  Google Scholar  * Lindorff-Larsen, K., Piana, S., Dror, R. O. & Shaw, D. E. How fast-folding proteins fold. _Science_ 334, 517–520 (2011).

Article  ADS  CAS  PubMed  Google Scholar  * Modig, K. et al. Detection of initiation sites in protein folding of the four helix bundle ACBP by chemical shift analysis. _FEBS Lett._ 581,

4965–4971 (2007). Article  CAS  PubMed  Google Scholar  * Cabrita, L. D., Hsu, S. T. D., Launay, H., Dobson, C. M. & Christodoulou, J. Probing ribosome–nascent chain complexes produced

in vivo by NMR spectroscopy. _Proc. Natl Acad. Sci. USA_ 106, 22239–22244 (2009). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Waudby, C. A. et al. Systematic mapping of free

energy landscapes of a growing filamin domain during biosynthesis. _Proc. Natl Acad. Sci. USA_ 115, 9744–9749 (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Burridge,

C. et al. Nascent chain dynamics and ribosome interactions within folded ribosome–nascent chain complexes observed by NMR spectroscopy. _Chem. Sci._ 12, 13120–13126 (2021). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Yu, F. & Sukenik, S. Structural preferences shape the entropic force of disordered protein ensembles. _J. Phys. Chem. B_ 127, 4235–4244 (2023).

Article  CAS  PubMed  PubMed Central  Google Scholar  * Dill, K. A. Dominant forces in protein folding. _Biochemistry_ 29, 7133–7155 (1990). Article  CAS  PubMed  Google Scholar  *

Geierhaas, C. D., Nickson, A. A., Lindorff-Larsen, K., Clarke, J. & Vendruscolo, M. BPPred: a Web-based computational tool for predicting biophysical parameters of proteins. _Protein

Sci._ 16, 125–134 (2007). Article  CAS  PubMed  PubMed Central  Google Scholar  * Bogunia, M. et al. Influence of temperature and salt concentration on the hydrophobic interactions of

adamantane and hexane. _J. Phys. Chem. B_ 126, 634–642 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Kudva, R. et al. The shape of the bacterial ribosome exit tunnel

affects cotranslational protein folding. _eLife_ 7, e36326 (2018). Article  PubMed  PubMed Central  Google Scholar  * Tan, R. et al. Folding stabilities of ribosome-bound nascent

polypeptides probed by mass spectrometry. _Proc. Natl Acad. Sci. USA_ 120, e2303167120 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Kelkar, D. A., Khushoo, A., Yang, Z.

& Skach, W. R. Kinetic analysis of ribosome-bound fluorescent proteins reveals an early, stable, cotranslational folding intermediate. _J. Biol. Chem._ 287, 2568–2578 (2012). Article 

CAS  PubMed  Google Scholar  * Nilsson, O. B. et al. Cotranslational folding of spectrin domains via partially structured states. _Nat. Struct. Mol. Biol._ 24, 221 (2017). Article  CAS 

PubMed  Google Scholar  * Hobbs, G. A., Der, C. J. & Rossman, K. L. RAS isoforms and mutations in cancer at a glance. _J. Cell Sci._ 129, 1287–1292 (2016). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Pai, E. F. et al. Refined crystal structure of the triphosphate conformation of H-ras p21 at 1.35 Å resolution: implications for the mechanism of GTP hydrolysis.

_EMBO J._ 9, 2351–2359 (1990). Article  CAS  PubMed  PubMed Central  Google Scholar  * Fowler, S. B. & Clarke, J. Mapping the folding pathway of an immunoglobulin domain: structural

detail from Phi value analysis and movement of the transition state. _Structure_ 9, 355–366 (2001). Article  CAS  PubMed  Google Scholar  * Tian, P. et al. Folding pathway of an Ig domain is

conserved on and off the ribosome. _Proc. Natl Acad. Sci. USA_ 115, E11284–E11293 (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hsu, S. T., Cabrita, L. D., Fucini,

P., Dobson, C. M. & Christodoulou, J. Structure, dynamics and folding of an immunoglobulin domain of the gelation factor (ABP-120) from _Dictyostelium discoideum_. _J. Mol. Biol._ 388,

865–879 (2009). Article  CAS  PubMed  Google Scholar  * Fu, J., Dang, Y., Counter, C. & Liu, Y. Codon usage regulates human KRAS expression at both transcriptional and translational

levels. _J. Biol. Chem._ 293, 17929–17940 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Zhang, J. & Matthews, C. R. The role of ligand binding in the kinetic folding

mechanism of human p21(H-ras) protein. _Biochemistry_ 37, 14891–14899 (1998). Article  CAS  PubMed  Google Scholar  * Quilliam, L. A. et al. Involvement of the switch 2 domain of Ras in its

interaction with guanine nucleotide exchange factors. _J. Biol. Chem._ 271, 11076–11082 (1996). Article  CAS  PubMed  Google Scholar  * Zou, Q., Habermann-Rottinghaus, S. M. & Murphy, K.

P. Urea effects on protein stability: hydrogen bonding and the hydrophobic effect. _Proteins_ 31, 107–115 (1998). Article  CAS  PubMed  Google Scholar  * Kuharski, R. A. & Rossky, P. J.

Solvation of hydrophobic species in aqueous urea solution — a molecular-dynamics study. _J. Am. Chem. Soc._ 106, 5794–5800 (1984). Article  CAS  Google Scholar  * O’Brien, E. P.,

Christodoulou, J., Vendruscolo, M. & Dobson, C. M. New scenarios of protein folding can occur on the ribosome. _J. Am. Chem. Soc._ 133, 513–526 (2011). Article  PubMed  Google Scholar  *

Vu, Q. V., Jiang, Y., Li, M. S. & O’Brien, E. P. The driving force for co-translational protein folding is weaker in the ribosome vestibule due to greater water ordering. _Chem. Sci._

12, 11851–11857 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Stein, K. C., Kriel, A. & Frydman, J. Nascent polypeptide domain topology and elongation rate direct the

cotranslational hierarchy of Hsp70 and TRiC/CCT. _Mol. Cell_ 75, 1117–1130.e1115 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Kramer, G., Shiber, A. & Bukau, B.

Mechanisms of cotranslational maturation of newly synthesized proteins. _Annu. Rev. Biochem._ 88, 337–364 (2019). Article  CAS  PubMed  Google Scholar  * Bertolini, M. et al. Interactions

between nascent proteins translated by adjacent ribosomes drive homomer assembly. _Science_ 371, 57–64 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Shiber, A. et al.

Cotranslational assembly of protein complexes in eukaryotes revealed by ribosome profiling. _Nature_ 561, 268–272 (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Wang,

F., Durfee, L. A. & Huibregtse, J. M. A Cotranslational ubiquitination pathway for quality control of misfolded proteins. _Mol. Cell_ 50, 368–378 (2013). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Shishido, H., Yoon, J. S., Yang, Z. & Skach, W. R. CFTR trafficking mutations disrupt cotranslational protein folding by targeting biosynthetic intermediates.

_Nat. Commun._ 11, 4258 (2020). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Urrutia, J. et al. An epilepsy-causing mutation leads to co-translational misfolding of the Kv7.2

channel. _BMC Biol._ 19, 109 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Tokuriki, N. & Tawfik, D. S. Stability effects of mutations and protein evolvability. _Curr.

Opin. Struct. Biol._ 19, 596–604 (2009). Article  CAS  PubMed  Google Scholar  * Tokuriki, N., Stricher, F., Serrano, L. & Tawfik, D. S. How protein stability and new functions trade

off. _PLoS Comput. Biol._ 4, e1000002 (2008). Article  ADS  PubMed  PubMed Central  Google Scholar  * Duttler, S., Pechmann, S. & Frydman, J. Principles of cotranslational ubiquitination

and quality control at the ribosome. _Mol. Cell_ 50, 379–393 (2013). Article  CAS  PubMed  Google Scholar  * Tokuriki, N. & Tawfik, D. S. Chaperonin overexpression promotes genetic

variation and enzyme evolution. _Nature_ 459, 668–673 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Williams, T. A. & Fares, M. A. The effect of chaperonin buffering on protein

evolution. _Genome Biol. Evol._ 2, 609–619 (2010). Article  PubMed  PubMed Central  Google Scholar  * Iyengar, B. R. & Wagner, A. Bacterial Hsp90 predominantly buffers but does not

potentiate the phenotypic effects of deleterious mutations during fluorescent protein evolution. _Genetics_ 222, iyac154 (2022). Article  PubMed  PubMed Central  Google Scholar  * Pechmann,

S. & Frydman, J. Interplay between chaperones and protein disorder promotes the evolution of protein networks. _PLoS Comput. Biol._ 10, e1003674 (2014). Article  ADS  PubMed  PubMed

Central  Google Scholar  * Alvarez-Ponce, D., Aguilar-Rodriguez, J. & Fares, M. A. Molecular chaperones accelerate the evolution of their protein clients in yeast. _Genome Biol. Evol._

11, 2360–2375 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Cassaignau, A. M. et al. A strategy for co-translational folding studies of ribosome-bound nascent chain

complexes using NMR spectroscopy. _Nat. Protoc._ 11, 1492–1507 (2016). Article  PubMed  Google Scholar  * Schagger, H. Tricine-SDS–PAGE. _Nat. Protoc._ 1, 16–22 (2006). Article  PubMed 

Google Scholar  * Delaglio, F. et al. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. _J. Biomol. NMR_ 6, 277–293 (1995). Article  CAS  PubMed  Google Scholar  *

Vranken, W. F. et al. The CCPN data model for NMR spectroscopy: development of a software pipeline. _Proteins_ 59, 687–696 (2005). Article  CAS  PubMed  Google Scholar  * Schanda, P., Kupce,

E. & Brutscher, B. SOFAST-HMQC experiments for recording two-dimensional heteronuclear correlation spectra of proteins within a few seconds. _J. Biomol. NMR_ 33, 199–211 (2005). Article

  CAS  PubMed  Google Scholar  * Chan, S. H. S., Waudby, C. A., Cassaignau, A. M. E., Cabrita, L. D. & Christodoulou, J. Increasing the sensitivity of NMR diffusion measurements by

paramagnetic longitudinal relaxation enhancement, with application to ribosome–nascent chain complexes. _J. Biomol. NMR_ 63, 151–163 (2015). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Stejskal, E. O. & Tanner, J. E. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. _J. Chem. Phys._ 42, 288 (1965). Article  ADS  CAS

  Google Scholar  * Ruckert, M. & Otting, G. Alignment of biological macromolecules in novel nonionic liquid crystalline media for NMR experiments. _J. Am. Chem. Soc._ 122, 7793–7797

(2000). Article  Google Scholar  * Schanda, P., Van Melckebeke, H. & Brutscher, B. Speeding up three-dimensional protein NMR experiments to a few minutes. _J. Am. Chem. Soc._ 128,

9042–9043 (2006). Article  CAS  PubMed  Google Scholar  * Lescop, E., Schanda, P. & Brutscher, B. A set of BEST triple-resonance experiments for time-optimized protein resonance

assignment. _J. Magn. Reson._ 187, 163–169 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Rasia, R. M., Lescop, E., Palatnik, J. F., Boisbouvier, J. & Brutscher, B. Rapid

measurement of residual dipolar couplings for fast fold elucidation of proteins. _J. Biomol. NMR_ 51, 369–378 (2011). Article  CAS  PubMed  Google Scholar  * Brutscher, B. Accurate

measurement of small spin-spin couplings in partially aligned molecules using a novel J-mismatch compensated spin-state-selection filter. _J. Magn. Reson._ 151, 332–338 (2001). Article  ADS

  CAS  PubMed  Google Scholar  * Ying, J., Delaglio, F., Torchia, D. A. & Bax, A. Sparse multidimensional iterative lineshape-enhanced (SMILE) reconstruction of both non-uniformly

sampled and conventional NMR data. _J. Biomol. NMR_ 68, 101–118 (2017). Article  CAS  PubMed  Google Scholar  * Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing

in Python. _Nat. Methods_ 17, 261–272 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hilser, V. J., Garcia-Moreno, E. B., Oas, T. G., Kapp, G. & Whitten, S. T. A

statistical thermodynamic model of the protein ensemble. _Chem. Rev._ 106, 1545–1558 (2006). Article  CAS  PubMed  Google Scholar  * Sun, H., Kay, L. E. & Tugarinov, V. An optimized

relaxation-based coherence transfer NMR experiment for the measurement of side-chain order in methyl-protonated, highly deuterated proteins. _J. Phys. Chem. B_ 115, 14878–14884 (2011).

Article  CAS  PubMed  Google Scholar  * Waudby, C. A., Burridge, C. & Christodoulou, J. Optimal design of adaptively sampled NMR experiments for measurement of methyl group dynamics with

application to a ribosome–nascent chain complex. _J. Magn. Reson._ 326, 106937 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Chan, S. H. S., Waudby, C. A. &

Christodoulou, J. NMR snapshots of nascent chains emerging from the ribosome during biosynthesis. Preprint at https://doi.org/10.26434/chemrxiv-2022-0lmsp (2022). * Cowieson, N. P. et al.

Beamline B21: high-throughput small-angle X-ray scattering at Diamond Light Source. _J. Synchrotron Radiat._ 27, 1438–1446 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Manalastas-Cantos, K. et al. ATSAS 3.0: expanded functionality and new tools for small-angle scattering data analysis. _J. Appl. Crystallogr._ 54, 343–355 (2021). Article  ADS  CAS  PubMed 

PubMed Central  Google Scholar  * Kopra, K. & Harma, H. Methods to monitor Ras activation state. _Methods Mol. Biol._ 2262, 137–167 (2021). Article  CAS  PubMed  Google Scholar  *

Killoran, R. C. & Smith, M. J. Conformational resolution of nucleotide cycling and effector interactions for multiple small GTPases determined in parallel. _J. Biol. Chem._ 294,

9937–9948 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH Image to ImageJ: 25 years of image analysis. _Nat.

Methods_ 9, 671–675 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Abraham, M. J. et al. GROMACS: high performance molecular simulations through multi-level parallelism from

laptops to supercomputers. _SoftwareX_ 1-2, 19–25 (2015). Article  ADS  Google Scholar  * Huang, J. et al. CHARMM36m: an improved force field for folded and intrinsically disordered

proteins. _Nat. Methods_ 14, 71–73 (2017). Article  CAS  PubMed  Google Scholar  * Robustelli, P., Piana, S. & Shaw, D. E. Developing a molecular dynamics force field for both folded and

disordered protein states. _Proc. Natl Acad. Sci. USA_ 115, E4758–E4766 (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hess, B., Bekker, H., Berendsen, H. J. C. &

Fraaije, J. G. E. M. LINCS: a linear constraint solver for molecular simulations. _J. Comput. Chem._ 18, 1463–1472 (1997). Article  CAS  Google Scholar  * Darden, T., York, D. &

Pedersen, L. Particle Mesh Ewald — an _N_.log(_N_) method for Ewald sums in large systems. _J. Chem. Phys._ 98, 10089–10092 (1993). Article  ADS  CAS  Google Scholar  * Bussi, G., Donadio,

D. & Parrinello, M. Canonical sampling through velocity rescaling. _J. Chem. Phys._ 126, 014101 (2007). Article  ADS  PubMed  Google Scholar  * Berendsen, H. J. C., Postma, J. P. M.,

Vangunsteren, W. F., Dinola, A. & Haak, J. R. Molecular-dynamics with coupling to an external bath. _J. Chem. Phys._ 81, 3684–3690 (1984). Article  ADS  CAS  Google Scholar  *

Parrinello, M. & Rahman, A. Polymorphic transitions in single-crystals — a new molecular-dynamics method. _J. Appl. Phys._ 52, 7182–7190 (1981). Article  ADS  CAS  Google Scholar  *

Noel, J. K. et al. SMOG 2: A versatile software package for generating structure-based models. _PLoS Comput. Biol._ 12, e1004794 (2016). Article  PubMed  PubMed Central  Google Scholar  *

McCoy, A. J., Fucini, P., Noegel, A. A. & Stewart, M. Structural basis for dimerization of the _Dictyostelium_ gelation factor (ABP120) rod. _Nat. Struct. Biol._ 6, 836–841 (1999).

Article  CAS  PubMed  Google Scholar  * Tesei, G., Schulze, T. K., Crehuet, R. & Lindorff-Larsen, K. Accurate model of liquid-liquid phase behavior of intrinsically disordered proteins

from optimization of single-chain properties. _Proc. Natl Acad. Sci. USA_ 118, e2111696118 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Rotkiewicz, P. & Skolnick, J.

Fast procedure for reconstruction of full-atom protein models from reduced representations. _J. Comput. Chem._ 29, 1460–1465 (2008). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Denning, E. J., Priyakumar, U. D., Nilsson, L. & Mackerell, A. D. Jr. Impact of 2′-hydroxyl sampling on the conformational properties of RNA: update of the CHARMM all-atom additive force

field for RNA. _J. Comput. Chem._ 32, 1929–1943 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Noeske, J. et al. High-resolution structure of the _Escherichia coli_

ribosome. _Nat. Struct. Mol. Biol._ 22, 336–341 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Javed, A. et al. Visualising nascent chain dynamics at the ribosome exit

tunnel by cryo-electron microscopy. Preprint at _bioRxiv_ https://doi.org/10.1101/722611 (2019). * Solomon, I. Relaxation processes in a system of 2 spins. _Phys. Rev._ 99, 559–565 (1955).

Article  ADS  CAS  Google Scholar  * Bloembergen, N. & Morgan, L. O. Proton relaxation times in paramagnetic solutions effects of electron spin relaxation. _J. Chem. Phys._ 34, 842

(1961). Article  ADS  CAS  Google Scholar  * Iwahara, J., Schwieters, C. D. & Clore, G. M. Ensemble approach for NMR structure refinement against H-1 paramagnetic relaxation enhancement

data arising from a flexible paramagnetic group attached to a macromolecule. _J. Am. Chem. Soc._ 126, 5879–5896 (2004). Article  CAS  PubMed  Google Scholar  * Gillespie, J. R. &

Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. II. Distance restraints from paramagnetic relaxation and calculation of an ensemble of

structures. _J. Mol. Biol._ 268, 170–184 (1997). Article  CAS  PubMed  Google Scholar  * Thomasen, F. E., Pesce, F., Roesgaard, M. A., Tesei, G. & Lindorff-Larsen, K. Improving Martini

3 for disordered and multidomain proteins. _J. Chem. Theory Comput._ 18, 2033–2041 (2022). Article  CAS  PubMed  Google Scholar  * Salmon, L. et al. NMR characterization of long-range order

in intrinsically disordered proteins. _J. Am. Chem. Soc._ 132, 8407–8418 (2010). Article  CAS  PubMed  Google Scholar  * Sezer, D., Freed, J. H. & Roux, B. Simulating electron spin

resonance spectra of nitroxide spin labels from molecular dynamics and stochastic trajectories. _J. Chem. Phys._ 128, 165106 (2008). Article  ADS  PubMed  PubMed Central  Google Scholar  *

Sezer, D., Freed, J. H. & Roux, B. Parametrization, molecular dynamics simulation, and calculation of electron spin resonance spectra of a nitroxide spin label on a polyalanine α-helix.

_J. Phys. Chem. B_ 112, 5755–5767 (2008). Article  CAS  PubMed  PubMed Central  Google Scholar  * Bruschweiler, R. et al. Influence of rapid intramolecular motion on NMR cross-relaxation

rates — a molecular-dynamics study of antamanide in solution. _J. Am. Chem. Soc._ 114, 2289–2302 (1992). Article  Google Scholar  * Polyhach, Y., Bordignon, E. & Jeschke, G. Rotamer

libraries of spin labelled cysteines for protein studies. _Phys. Chem. Chem. Phys._ 13, 2356–2366 (2011). Article  CAS  PubMed  Google Scholar  * Tesei, G. et al. DEER-PREdict: software for

efficient calculation of spin-labeling EPR and NMR data from conformational ensembles. _PLoS Comput. Biol._ 17, e1008551 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Stelzl, L. S., Fowler, P. W., Sansom, M. S. & Beckstein, O. Flexible gates generate occluded intermediates in the transport cycle of LacY. _J. Mol. Biol._ 426, 735–751 (2014). Article 

CAS  PubMed  PubMed Central  Google Scholar  * Newby, F. N. et al. Structure-free validation of residual dipolar coupling and paramagnetic relaxation enhancement measurements of disordered

proteins. _Biochemistry_ 54, 6876–6886 (2015). Article  CAS  PubMed  Google Scholar  * Lavalette, D., Amand, B. & Pochon, F. Rotational relaxation of 70S ribosomes by a depolarization

method using triplet probes. _Proc. Natl Acad. Sci. USA_ 74, 1407–1411 (1977). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Pyka, J., Ilnicki, J., Altenbach, C., Hubbell, W.

L. & Froncisz, W. Accessibility and dynamics of nitroxide side chains in T4 lysozyme measured by saturation recovery EPR. _Biophys. J._ 89, 2059–2068 (2005). Article  ADS  CAS  PubMed 

PubMed Central  Google Scholar  * Jun, S., Becker, J. S., Yonkunas, M., Coalson, R. & Saxena, S. Unfolding of alanine-based peptides using electron spin resonance distance measurements.

_Biochemistry_ 45, 11666–11673 (2006). Article  CAS  PubMed  Google Scholar  * Thomas, D. D., Dalton, L. R. & Hyde, J. S. Rotational diffusion studied by passage saturation transfer

electron paramagnetic resonance. _J. Chem. Phys._ 65, 3006–3024 (1976). Article  ADS  CAS  Google Scholar  * Hummer, G. & Kofinger, J. Bayesian ensemble refinement by replica simulations

and reweighting. _J. Chem. Phys._ 143, 243150 (2015). Article  ADS  PubMed  Google Scholar  * Kofinger, J. et al. Efficient ensemble refinement by reweighting. _J. Chem. Theory Comput._ 15,

3390–3401 (2019). Article  PubMed  PubMed Central  Google Scholar  * Hansen, P. C. & Oleary, D. P. The use of the L-curve in the regularization of discrete III-posed problems. _SIAM J.

Sci. Comput._ 14, 1487–1503 (1993). Article  MathSciNet  Google Scholar  * Bottaro, S., Bengtsen, T. & Lindorff-Larsen, K. Integrating molecular simulation and experimental data: a

Bayesian/maximum entropy reweighting approach. _Methods Mol. Biol._ 2112, 219–240 (2020). Article  CAS  PubMed  Google Scholar  * Nygaard, M., Kragelund, B. B., Papaleo, E. &

Lindorff-Larsen, K. An efficient method for estimating the hydrodynamic radius of disordered protein conformations. _Biophys. J._ 113, 550–557 (2017). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Ortega, A., Amoros, D. & de la Torre, J. G. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models.

_Biophys. J._ 101, 892–898 (2011). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Michaud-Agrawal, N., Denning, E. J., Woolf, T. B. & Beckstein, O. MDAnalysis: a toolkit

for the analysis of molecular dynamics simulations. _J. Comput. Chem._ 32, 2319–2327 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Ahmed, M. C., Crehuet, R. &

Lindorff-Larsen, K. Computing, analyzing, and comparing the radius of gyration and hydrodynamic radius in conformational ensembles of intrinsically disordered proteins. _Methods Mol. Biol._

2141, 429–445 (2020). Article  CAS  PubMed  Google Scholar  * Han, B., Liu, Y., Ginzinger, S. W. & Wishart, D. S. SHIFTX2: significantly improved protein chemical shift prediction. _J.

Biomol. NMR_ 50, 43–57 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Zweckstetter, M. NMR: prediction of molecular alignment from structure using the PALES software. _Nat.

Protoc._ 3, 679–690 (2008). Article  CAS  PubMed  Google Scholar  * Grudinin, S., Garkavenko, M. & Kazennov, A. Pepsi-SAXS: an adaptive method for rapid and accurate computation of

small-angle X-ray scattering profiles. _Acta Crystallogr. D_ 73, 449–464 (2017). Article  ADS  CAS  Google Scholar  * Pesce, F. & Lindorff-Larsen, K. Refining conformational ensembles of

flexible proteins against small-angle x-ray scattering data. _Biophys. J._ 120, 5124–5135 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * McGibbon, R. T. et al. MDTraj:

a modern open library for the analysis of molecular dynamics trajectories. _Biophys. J._ 109, 1528–1532 (2015). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Best, R. B.,

Hummer, G. & Eaton, W. A. Native contacts determine protein folding mechanisms in atomistic simulations. _Proc. Natl Acad. Sci. USA_ 110, 17874–17879 (2013). Article  ADS  CAS  PubMed 

PubMed Central  Google Scholar  * Dima, R. I. T. D. Asymmetry in the shapes of folded and denatured states of proteins. _J. Phys. Chem. B_ 108, 6564–6570 (2004). Article  CAS  Google Scholar

  * Kabsch, W. & Sander, C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. _Biopolymers_ 22, 2577–2637 (1983). Article  CAS 

PubMed  Google Scholar  * Daura, X. et al. Peptide folding: when simulation meets experiment. _Angew Chem. Int. Ed._ 38, 236–240 (1999). Article  CAS  Google Scholar  * Baxa, M. C.,

Haddadian, E. J., Jumper, J. M., Freed, K. F. & Sosnick, T. R. Loss of conformational entropy in protein folding calculated using realistic ensembles and its implications for NMR-based

calculations. _Proc. Natl Acad. Sci. USA_ 111, 15396–15401 (2014). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hilser, V. J. & Whitten, S. T. Using the COREX/BEST server

to model the native-state ensemble. _Methods Mol. Biol._ 1084, 255–269 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Theisen, F. F. et al. Quantification of conformational

entropy unravels effect of disordered flanking region in coupled folding and binding. _J. Am. Chem. Soc._ 143, 14540–14550 (2021). Article  CAS  PubMed  Google Scholar  * Lin, S. T., Maiti,

P. K. & Goddard, W. A. III. Two-phase thermodynamic model for efficient and accurate absolute entropy of water from molecular dynamics simulations. _J. Phys. Chem. B_ 114, 8191–8198

(2010). Article  CAS  PubMed  Google Scholar  * Caro, M. A., Laurila, T. & Lopez-Acevedo, O. Accurate schemes for calculation of thermodynamic properties of liquid mixtures from

molecular dynamics simulations. _J. Chem. Phys._ 145, 244504 (2016). Article  ADS  PubMed  Google Scholar  * Streit, J. O. The ribosome lowers the entropic penalty of protein folding.

_Zenodo_ https://doi.org/10.5281/zenodo.11618750 (2024). * Nielsen, J. T. & Mulder, F. A. A. POTENCI: prediction of temperature, neighbor and pH-corrected chemical shifts for

intrinsically disordered proteins. _J. Biomol. NMR_ 70, 141–165 (2018). Article  CAS  PubMed  Google Scholar  * Riback, J. A. et al. Innovative scattering analysis shows that hydrophobic

disordered proteins are expanded in water. _Science_ 358, 238–241 (2017). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Camilloni, C., De Simone, A., Vranken, W. F. &

Vendruscolo, M. Determination of secondary structure populations in disordered states of proteins using nuclear magnetic resonance chemical shifts. _Biochemistry_ 51, 2224–2231 (2012).

Article  CAS  PubMed  Google Scholar  * Cox, J. D., Wagman, D. D. & Medvedev, V. A. _CODATA Key Values for Thermodynamics_ (Hemisphere Publishing, 1989). Download references

ACKNOWLEDGEMENTS This work was supported by a Wellcome Trust Investigator Award (to J.C., 206409/Z/17/Z). The authors thank I. Chen (St. Jude Research) for helpful general comments on the

manuscript; M. Smith (Université de Montréal) for the gift of the plasmid encoding the protein SOScat; and S. Mukherjee and L. Schäfer (Ruhr University Bochum) for advice on the water

entropy calculations. We acknowledge use of the UCL Biomolecular NMR Centre. The Francis Crick Institute is also acknowledged for provision of access to the MRC Biomedial NMR Centre and

receives its core funding from Cancer Research UK (FC001029), the UK Medical Research Council (FC001029) and the Wellcome Trust (FC001029). J.O.S. was supported by a BBSRC London

Interdisciplinary Biosciences Doctoral Programme studentship. L.F.W. and C.R.H. were supported by MRC Doctoral Training studentships. We thank Diamond and N. Cowieson for access and

technical help to acquire the SAXS data on the B21 beamline. This project made use of time on HPC resources on Archer2 (ARCHER2 UK National Supercomputing service, https://www.archer2.ac.uk)

granted via the UK High-End Computing Consortium for Biomolecular Simulation, HECBioSim (https://www.hecbiosim.ac.uk), supported by EPSRC (grant no. EP/R029407/1 and EP/X035603/1). We also

acknowledge the EuroHPC Joint Undertaking for awarding this project access to the EuroHPC supercomputer LUMI, hosted by CSC (Finland) and the LUMI consortium through a EuroHPC Regular Access

call and the Baskerville Tier 2 HPC service (https://www.baskerville.ac.uk/). Baskerville was funded by the EPSRC and UKRI through the World Class Labs scheme (EP/T022221/1) and the Digital

Research Infrastructure programme (EP/W032244/1) and is operated by Advanced Research Computing at the University of Birmingham. We additionally acknowledge the use of the UCL Myriad and

Kathleen High Performance Computing Facility (Myriad@UCL and Kathleen@UCL), and associated support services, in the completion of this work. AUTHOR INFORMATION Author notes * These authors

contributed equally: Julian O. Streit, Ivana V. Bukvin, Sammy H. S. Chan AUTHORS AND AFFILIATIONS * Institute of Structural and Molecular Biology, Department of Structural and Molecular

Biology, University College London, London, UK Julian O. Streit, Ivana V. Bukvin, Sammy H. S. Chan, Shahzad Bashir, Lauren F. Woodburn, Tomasz Włodarski, Angelo Miguel Figueiredo, Gabija

Jurkeviciute, Haneesh K. Sidhu, Charity R. Hornby, Christopher A. Waudby, Lisa D. Cabrita, Anaïs M. E. Cassaignau & John Christodoulou * Department of Biological Sciences, Birkbeck

College, London, UK John Christodoulou Authors * Julian O. Streit View author publications You can also search for this author inPubMed Google Scholar * Ivana V. Bukvin View author

publications You can also search for this author inPubMed Google Scholar * Sammy H. S. Chan View author publications You can also search for this author inPubMed Google Scholar * Shahzad

Bashir View author publications You can also search for this author inPubMed Google Scholar * Lauren F. Woodburn View author publications You can also search for this author inPubMed Google

Scholar * Tomasz Włodarski View author publications You can also search for this author inPubMed Google Scholar * Angelo Miguel Figueiredo View author publications You can also search for

this author inPubMed Google Scholar * Gabija Jurkeviciute View author publications You can also search for this author inPubMed Google Scholar * Haneesh K. Sidhu View author publications You

can also search for this author inPubMed Google Scholar * Charity R. Hornby View author publications You can also search for this author inPubMed Google Scholar * Christopher A. Waudby View

author publications You can also search for this author inPubMed Google Scholar * Lisa D. Cabrita View author publications You can also search for this author inPubMed Google Scholar *

Anaïs M. E. Cassaignau View author publications You can also search for this author inPubMed Google Scholar * John Christodoulou View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS Conceptualization: J.O.S., I.V.B., S.H.S.C., T.W., C.A.W., A.M.E.C., L.D.C. and J.C. Methodology: J.O.S., I.V.B., S.H.S.C., C.A.W., T.W., A.M.E.C.,

L.D.C. and J.C. Investigation: J.O.S., I.V.B., S.H.S.C., S.B., L.F.W., A.M.F., G.J., H.K.S., C.R.H., A.M.E.C., L.D.C. and J.C. Visualization: J.O.S., I.V.B. and S.H.S.C. Funding acquisition:

J.O.S., A.M.E.C., T.W., L.D.C. and J.C. Project administration: A.M.E.C., L.D.C. and J.C. Supervision: S.H.S.C., T.W., C.A.W., A.M.E.C., L.D.C. and J.C. Writing the original draft: J.O.S.,

L.D.C. and J.C. Reviewing the paper and editing: J.O.S., I.V.B., S.H.S.C., L.D.C. and J.C. CORRESPONDING AUTHORS Correspondence to Sammy H. S. Chan, Anaïs M. E. Cassaignau or John

Christodoulou. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature_ thanks the anonymous reviewer(s) for their

contribution to the peer review of this work. Peer reviewer reports are available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. EXTENDED DATA FIGURES AND TABLES EXTENDED DATA FIG. 1 PRE ANALYSIS OF UNFOLDED FLN5 ON AND OFF THE RIBOSOME. (A) Schematics of the

constructs used for the PRE experiments. The RNC is comprised of an N-terminal His-tag (for purification), FLN5 A3A3, the subsequent domain FLN6, and an enhanced version of the SecM-AE1

stalling sequence6,7. The FLN5 A3A3 mutant was previously described7. (B) (Left) The annotated crystal structure (PDB 1QFH93) is shown from two views towards the two main β-sheets,

highlighting the PRE labelling sites used for both the isolated protein and the RNC. (Right) The secondary structure of folded FLN5 and labelling sites are shown. (C) Region of an exemplar

1H-15N HMQC NMR spectrum of isolated FLN5 A3A3 spin-labelled at C657 (see Supplementary Fig. 1 for full spectrum). The paramagnetic and diamagnetic spectrum are overlayed. (D) PRE intensity

ratio profiles for six different labelling sites (indicated with the black star) on (blue) and off (black) the ribosome. NMR data were recorded at 800 MHz, 283 K. Theoretical reference

profiles expected for a fully extended polypeptide are also shown as dashed lines (see methods). The secondary structure elements (β-strands) of native FLN5 are indicated at the top. The

shaded region at the C-terminus represents the region of FLN5 that is broadening beyond detection through ribosome interactions (N730-K746, in the RNC)7. The second panel with grey bars

under each dataset shows the difference between the RNC and isolated data. (E) (Top) The annotated crystal structure (PDB 1QFH93) of FLN5 is shown with two additional labelling sites used

for the RNC construct. (Bottom) Annotated MTSL labelling sites (yellow circles) on the ribosome structure near the exit tunnel. (F) PRE intensity ratio profiles for the two addition

labelling sites within FLN5 A3A3 and two ribosomal MTSL labelling sites recorded at 800 MHz, 283 K. All data show the fitted mean NMR intensities ± RMSE propagated from spectral noise. See

Supplementary Fig. 1 for NMR spectra. Source data EXTENDED DATA FIG. 2 MTSL LABELLING, QUALITY CONTROL AND OPTIMISATION OF PRE-NMR EXPERIMENTS. (A-B) Mass spectrometry analysis of

MTSL-labelled FLN5 A3A3 cysteine variants C699 V747 (A) and C744 V747 (B). Black arrows indicate the mass of unlabelled FLN5 A3A3 and red arrows the mass of MTSL-labelled protein. (C)

Fluorescent gel (12% BisTris) of purified 70 S and RNC (FLN5 + 31 A3A3 C699 V747) samples labelled with a fluorescent MTSL analogue (ABD-MTS) at pH 8.0 for the indicated time. The gel shows

a distinct band for the NC in addition to the ribosome background. Ribosomal proteins are also annotated based on molecular weight estimates. The experiment was performed three times (n = 3)

and a representative gel image is shown (see supplementary information, Supplementary Fig. 2 for uncropped gel images). (D) Representative anti-hexahistidine western blot (12% BisTris gel)

of FLN5 + 31 A3A3 V747 with a cysteine at C699 and C744 during reaction time-course with molar excess (10000x) of PEG maleimide at pH 7.5 to probe the accessibility and reactivity of the

cysteine variants. The fraction PEGylated (mean ± SD; n = 2 for C699; n = 3 for C744) was estimated by densitometry and plotted as a function of time (see supplementary information,

Supplementary Fig. 3 for uncropped gel images). (E) A representative Coomassie and fluorescent gel (20% Tricine) of purified WT, L23 G90C and L24 N53C 70 S ribosomes after overnight

incubation with 10x molar excess fluorescein maleimide at pH 7.5. (See supplementary information, Supplementary Fig. 4 for uncropped gel images; n = 2 for L23 G90C; n = 3 for WT and L24

N53C). (F) PRE intensity ratios of the FLN5 + 31 A3A3 variant without any cysteines in the NC (C747V, Δcys). (G) Chemical shift perturbations (CSPs) along the protein sequence for all

MTSL-labelled isolated protein (upper row) and RNC (lower row) variants measured in the 1H-15N SOFAST-HMQC spectra of FLN5 + 31 A3A3 RNC cysteine variants relative to the isolated FLN5 A3A3

protein and the FLN5 + 31 A3A3 RNC, respectively. The labelling sites are indicated with a star (*). The dotted line indicates a threshold of 0.06 ppm. (H) Integrity of RNCs during PRE

experiments was monitored with 15N-SORDID diffusion measurements. The calculated diffusion coefficient D is shown throughout NMR acquisition (centre), highlighting the paramagnetic (grey)

and the diamagnetic acquisition timeframe (red). (I) Optimisation of the recycle delay (d1) time chosen for PRE SOFAST-HMQC experiments to provide maximum sensitivity while also allowing the

signal to relax completely before the subsequent scan is initiated. 1D 1H spectra at d1 values ranging from 50-800 ms (top, yellow to red gradient); total signal intensity dependence on the

d1 value (middle); time-averaged signal (bottom). 450 ms was chosen for PRE experiments. (J) Diffusion coefficients of the DSS reference and isolated FLN5 A3A3 in different concentrations

of glycerol. The extracted radius of hydration (Rh) for the protein is also shown. The values at 5% and 18% of glycerol were calculated taking into account the increase in viscosity from the

DSS diffusion measurements. (K) PRE analysis of isolated FLN5 A3A3 C740 V747 in different concentrations of glycerol. The upper panel shows all individual datapoints while the lower panel

shows the data averaged over a window of three residues for ease of visualisation. (L) Theoretical effect of increasing viscosity on the PRE intensity ratios (Ipara/Idia). The upper panel

shows the predicted PRE profile of the FLN5 A3A3 ensemble obtained after reweighting using different values of τC (shown in legend in nanoseconds) and the lower panel shows an overlay of the

experimental data at 0 and 18% glycerol with the MD profiles using τC of 3 and 12 ns. (M) Theoretical effect of increasing residue-specific τC values towards the C-terminus for a tethered

polymer, using Eq. S16 and \({S}_{{NC}}^{2}\) = _(1/d) x_ \({S}_{{NC},{\max }}^{2}\) where _d_ is the distance to the C-terminal residue (in amino acids) and \({S}_{{NC},{\max }}^{2}\) the

maximum order parameter that the C-terminal residue can reach (set to 0.1 for this illustrative example). The top plot shows the experimental RNC PRE-NMR data and isolated PREs (computed

from the reweighted MD ensemble) with either a uniform _τ__C_ of 3 ns across the sequence or the tethering _τ__C_ values from the panel below. Unless otherwise indicated, all NMR data are

presented as the fitted mean ± RMSE propagated from the spectral noise. Source data EXTENDED DATA FIG. 3 ANALYSIS AND REWEIGHTING OF MD SIMULATIONS FOR ISOLATED FLN5 A3A3. (A) Probability

distributions of the all-atom radius of gyration (Rg) for the different ensembles (mean ± SEM from block averaging). (B) Probability distributions of the fraction of native contacts (Q,

relative to natively folded FLN5, mean ± SEM from block averaging). (C) Ensemble-averaged properties including Rg, Q and secondary structure populations are summarised (mean ± SEM from block

averaging). (D) Average secondary structure propensities (mean ± SEM from block averaging) along the protein sequence determined using the DSSP algorithm (C = coil, E = strand, H =

helix)131. The vertical shaded areas highlight the regions of β-strands (annotated as strands A-G) in natively folded FLN5. (E) Average contact maps of the ensembles (zoomed in to a

probability of 0.2 for clarity). Contacts were defined as Cα- Cα distances of less than 10 Å. The black contours highlight the native contact map of folded FLN5. Above and below the diagonal

are identical. (F) Overlay of experimental data (shown in transparent orange bars) with the calculated PREs of the four ensemble before and after (H) reweighting. Colours are as in panels

A-B. (G) Determination of optimal τC for each ensemble by computing the reduced _χ_2 statistic against the experimental PRE-NMR data (Extended Data Fig. 1). Values of _τ__C_ were scanned in

steps of 1 ns from 1 to 15 ns and the optimal value found is displayed in the figure legend. Colours are as in panels A-B. (I) L-curve analysis to identify an optimal balance between the

prior ensemble and agreement with experimental data117. The entropy term on the x-axis represents the Kullback-Leibler divergence and quantifies the extent of deviation from the prior

ensemble. The optimal value of _τ__c_ as determined from the prior ensemble as well as the _χ_2, RMSD and _N__eff_ (fraction of effective frames contributing to the ensemble average

calculated as ln(-Entropy)119) are displayed in each panel for the corresponding elbow of the L-curve, which is the final solution chosen from the reweighting analysis (see methods). Source

data EXTENDED DATA FIG. 4 VALIDATION OF THE ENSEMBLES AGAINST ORTHOGONAL DATA NOT USED IN THE REWEIGHTING PROCESS. (A) Diffusion coefficients (mean ± RMSE propagated from NMR intensity fits)

and radius of hydration (Rh) (see methods) as measured for folded FLN5, FLN5 A3A3 and the unfolded state of FLN5Δ6, a previously characterised truncation variant24. (B) Comparison between

the experimental Rh (32.6 ± 0.1 Å, plotted as a horizontal line in magenta) and the calculated Rh of the ensembles before (black bar) and after (yellow bar) reweighting. The error bars

represent the uncertainty around the ensemble average expected from the forward model (see methods). The right panel shows the corresponding _χ_2 values, quantifying the agreement with the

experimental data. (C) Secondary Cα chemical shifts of FLN5 A3A3 using the random coil shifts predicted by POTENCI139. (D) Comparison between experimental and calculated chemical shifts from

the MD ensembles before (black bars) and after (yellow bar) reweighting for each nucleus. The table above the plot summarises a global agreement score, calculated by adding the nucleus

specific RMSD values normalised by the error of the forward model. The forward model error is plotted as a horizontal line in the bar plots, taken as the RMSE values reported by the

method124. (E) Comparison between the experimental RDCs (grey bars) measured in PEG/octanol with the simulated RDCs before (dotted line) and after reweighting with the PRE data (solid line).

The RDC Q-factors are used to quantify the agreement. (F) Guinier region and linear fit (red line) to the experimental SAXS data (black circles). The bottom plot shows the residuals. (G)

Experimental SAXS profile shown as a double log plot (mean ± errors propagated as determined by the ATSAS package80). (H) Ensemble-averaged Rg values obtained from the MD ensembles before

(prior) and after reweighting (posterior) compared with the experimental value from the Guinier analysis in panel F, obtained with the autorg tool80, and the molecular form factor (MFF)

analysis140. (I) Comparison of the experimental and theoretical SAXS profiles obtained from the MD ensembles before and after reweighting. The goodness of fit is quantified with the reduced

_χ__2_ and residuals are shown below the main plot for the prior and posterior ensembles. (J) CD spectrum of isolated FLN5 A3A3 recorded at 283 K. (K) Secondary structure populations

obtained from the NMR chemical shifts with δ2D141 compared with average populations observed in the MD ensembles before (in parantheses) and after reweighting (mean ± SEM from block

averaging). Source data EXTENDED DATA FIG. 5 ANALYSIS OF UNFOLDED STATE ENSEMBLE ON THE RIBOSOME OBTAINED FROM ALL-ATOM MD SIMULATIONS. (A) Modelling of MTSL rotamer distribution on ribosome

labelling sites uL23 G90C and uL24 N53C. Ten _E. coli_ ribosome PDB models (highest resolution models available to date: 4YBB, 6PJ6, 6XZ7, 7K00, 7LVK, 7N1P, 7O1A, 7PJS, 7Z20, 7ZP8) were

aligned to the simulation ribosome frame in PyMOL (v2.3). For each ribosome model, MTSL rotamers were fitted to the labelling sites as described in methods. The transparent cloud represents

the rotamer cloud from these ten ribosome models, highlighting how small fluctuations in the labelling site can lead to different rotamer distributions. R1 represents the rotamer

distribution fitted to the ribosome model utilised in the all-atom MD simulations, while R2 is the rotamer distribution fitted to the ribosome model utilised in our previous work6. We find

the RNC ensembles to be in better agreement after reweighting with the R2 rotamer distribution compared to the R1 distribution and used the R2 distribution for the results presented here.

(B) Bayesian reweighting of the FLN5 + 31 A3A3 RNC ensemble using the experimental PRE data is shown (see methods). The final _χ_2 and _N__eff_ obtained at the elbow of the curve are shown

on the plot. (C) Comparison of back-calculated PREs from MD and the experimental data (black bars, Extended Data Fig. 1) before (dotted blue line) and after reweighting (solid blue line).

(D) Secondary Cα chemical shifts of FLN5 + 31 A3A3 measured at 283 K using the POTENCI random coil values139. (E) Average agreement (reported as the RMSD in ppm) between MD (calculated) and

experimental chemical shifts before (black) and after (yellow) reweighting with the PRE data. The dotted horizontal line represents the error of the forward model124. (F) β-strand secondary

structure propensity (mean ± SEM from block averaging). (G) NC interactions with the ribosome mapped onto the surface of the ribosome. (H) Left: Interactions between the NC and ribosome

surface along the protein sequence (mean ± SEM from block averaging). The black cross indicates the experimentally estimated interaction for the C-terminal binding site (within the dotted

rectangle) from our previous work7. Right: A comparison of amide S2 order parameters from MD simulations with relative NMR intensities7 further supports the accuracy of NC-ribosome

interactions observed in the MD simulations. The decrease in NMR intensities towards the C-terminus around residue 720 coincides with an increase in the amide _S_2 (restricted dynamics due

to ribosome binding). A steric-only model (see methods) does not predict this increase correctly, only showing an increase in the amide _S_2 around at ~residue 740. (I-J) The

residue-specific interaction contributions from Lennard-Jones (LJ) and Coulombic energies (mean ± SEM from block averaging) of the N-terminal (I) and C-terminal (J) ribosome-binding segments

are shown. Ribosome interactions are driven by positively charged C-terminal residues (R734, K739, K746) with the rRNA and E749 interacting with RNA-bound Mg2+ ions and K47 within the uL24

loop. (K) Analysis of intramolecular contacts within FLN5 A3A3 on and off the ribosome between different types of residues (oppositely charged and hydrophobic). (L-M) Probability

distributions of the FLN5 A3A3 steric-only model on and off the ribosome and comparison between the steric-only model and C36m+W ensemble of the NC-ribosome interaction probability along the

FLN5 sequence (mean ± SEM from block averaging). (N) Rg and (O) SASA probability distributions for isolated and RNC FLN5 A3A3 before reweighting (prior) and after reweighting with different

datasets (see Supplementary Tables 2–4). Source data EXTENDED DATA FIG. 6 ENTROPY ANALYSIS OF THE UNFOLDED STATE ON AND OFF THE RIBOSOME. (A) Convergence of the number of clusters visited

(see methods for clustering details) for several different cut-off values was assessed by plotting number of clusters as a function of simulation time. This confirmed that for the higher

cut-off values (1.4–1.8 nm), sampling has been sufficient to reach a plateau in the number of clusters visited. This was analysed to ensure that differences between the RNC and isolated

protein are not due to differences in sampling. (B) The average Gibbs entropy (\(-{\sum }_{i}^{n}{p}_{i}\,\times {\rm{ln}}\left({p}_{i}\right)\), where n is the number of

clusters/microstates and p the population of each microstate) was then estimated from the full ensembles after reweighting with the PRE data. (C) and (D) show the same analysis as in panels

A-B but for a simple all-atom steric model of the unfolded state (see Methods). (E) Exemplar Ramachandran free energy landscapes of A721 on and off the ribosome. (F) The average entropy (S)

summed over all residues for each ensemble is shown (mean ± SEM from block averaging). The average difference per residue is shown above the plot. Structures were sampled every 20 ps with

equal statistical weights (to avoid differences due to differences in reweighting between the ensembles). (G) The resulting effect on free energy (−TΔS for the entire protein at 298 K, mean 

± SEM) was calculated using different block sizes of total sampling and number of bins (legend of plot). We observe a convergence towards +1.9 ± 0.2 kcal mol−1 (estimated from 7.5 μs

sampling and 50 bins). (H) Asphericity (Δ, see methods) of the ensembles shown as probability distributions (mean ± SEM from block averaging). (I) Probability distribution (mean ± SEM from

block averaging) of the total (i), apolar (ii) and polar (iii) solvent-accessible surface area (SASA) of FLN5 (residues 646–750) is shown for each ensemble. (iv) The thermodynamic parameters

of the solvation free energy difference between the unfolded state on and off the ribosome were calculated based on the apolar and polar changes in surface area and

experimentally-parameterised functions of the heat capacity, _C__p_, entropy, _S_, and enthalpy, _H_75,134,135 (see methods for more details). (J) Average radial distribution function of the

protein (all atoms) to water (centre of mass) distance for the isolated and RNC ensemble. The vertical line represents the 3.5 Å distance cut-off chosen to define the hydration layer

consisting of the first and second hydration shell. (K) Probability distributions of the number of water molecules in the first hydration layer before (dashed line) and after (solid line)

reweighting with PRE-NMR data and (L) ensemble-averaged number of water molecules in the hydration layer (mean ± SEM from block averaging). (M) Molar water entropy of obtained with the

two-phase thermodynamic method (2PT) as a function of distance from the FLN5 A3A3 protein at 283 K for both the C36m and C36m+W parameters (which differ only in their water hydrogen LJ

parameter). The horizontal line represents the bulk molar entropy of water obtained from a pure water box at 283 K (panel O). The solvation entropy (Ssolv) is the difference of the molar

entropy of water in the hydration layer (0–3.5 Å) and in bulk (36–46 Å value used). Values are shown as mean ± SEM obtained from five independent simulations (n = 5, see Methods). (N) Molar

water entropy as a function of distance from the FLN5 A3A3 protein with the C36m+W force field at 283 and 298 K (mean ± SEM from n = 5). Their respective bulk values obtained from pure water

boxes (panel P) are shown as horizontal lines. (O) Comparison of molar entropy of water obtained from experiments142, in previous work in the literature with the TIP3P water model136, and

values obtained in this work with C36m and C36m+W at 298 K (mean ± SEM form n = 5). (P) Difference in solvation entropy on and off the ribosome (RNC-isolated, mean ± SEM) obtained by using

the solvation entropies per water molecule from panel N and difference in the number of water molecules in the hydration shells of the RNC and isolated ensemble (see methods). This quantity

is shown for the ensembles before (prior) and after (posterior) reweighting with PRE-NMR data. Source data EXTENDED DATA FIG. 7 DEPENDENCE OF THE FOLDING EQUILIBRIUM CONSTANT ON TEMPERATURE

AND STRUCTURAL PERTURBATIONS OBSERVED IN THE NATIVE STATE ON THE RIBOSOME. (A-B) 19F NMR spectra of FLN5 on and off (Δ6 truncation) the ribosome recorded at a 19F-Larmor frequency of 470 

MHz. Raw spectra are shown in grey, lineshape fits in colour and the total fit in black. Residuals after fitting are shown below each spectrum. (C-D) Nonlinear fits to a modified

Gibbs-Helmholtz equation (see methods) of the equilibrium constants on and off the ribosome measured by 19F NMR (from panels A-B) shown as the mean ± SEM propagated from NMR line shape fits

(panel C) and the resulting thermodynamic parameters (mean ± SD from fits, panel D). (E-F) 19F NMR spectra of the FLN5 mutant E6 on and off the ribosome (Δ2 truncation) recorded at a

19F-Larmor frequency of 470 MHz. The FLN5Δ2 E6 was chosen due to its suitable stability in this temperature range to quantify both [U] and [N]. Raw spectra are shown in grey, lineshape fits

in colour and the total fit in black. Residues after fitting are shown below each spectrum. (G-H) Nonlinear fits to a modified Gibbs-Helmholtz equation (see methods) of the equilibrium

constants on and off the ribosome measured by 19F NMR (from panels E-F) shown as the mean ± SEM propagated from NMR line shape fits (panel G) and the resulting thermodynamic parameters (mean

 ± SD from fits, panel H). (I) Left: Chemical shift perturbations (CSPs) measured by NMR (1H-13C HMQC) for methyl groups of natively folded FLN5 (RNCs relative to the isolated protein)25.

The black datapoints represent the mean ± SD from five different RNC lengths for ease for visualisation. Right: Average CSPs mapped on the crystal structure of FLN593. (J) CSPs (RNC relative

to isolated protein) measured for FLN5 labelled with three different 19F-tfmF labelling sites by 19F NMR at linker lengths of 47 and 67 amino acids6. (K) Correlation plots (along with

Pearson correlation coefficients) of methyl relaxation parameters (\({S}_{{axis}}^{2}\)_τ__C_) for natively folded FLN525 in different concentrations of glycerol (left panel) and correlating

FLN5 on and off the ribosome (right panel). Source data EXTENDED DATA FIG. 8 EXPANSION AND ENTROPIC DESTABILISATION OF THE UNFOLDED STATE ON THE RIBOSOME PERSIST AT LONGER NC LINKER

LENGTHS. (A-C) PRE-NMR analysis of FLN5 A3A3 (labelled at C740, black star) in isolation and at three different RNC linker lengths (FLN5 + 31, FLN5 + 47, FLN5 + 67). Panel A shows a window

average over three residues for ease of visualisation. Panels B and C show all datapoints as the fitted mean ± RMSE propagated from spectral noise. The colour scheme in panels B-C is the

same as in panel A. Theoretical reference profiles expected for a fully extended polypeptide are also shown as dashed lines. The shaded region at the C-terminus represents the region of FLN5

that is broadening beyond detection through ribosome interactions (N730-K746, in the RNC)7. (D-E) 19F NMR spectra of FLN5 (F672A) on and off the ribosome recorded at a 19F-Larmor frequency

of 470 MHz. A destabilising variant (F672A) is used to enable measurements of the unfolded state populations at FLN5 + 67. Raw spectra are shown in grey, lineshape fits in colour and the

total fit in black. Residuals after fitting are shown below each spectrum. (F) Nonlinear fit to a modified Gibbs-Helmholtz equation of the equilibrium constants on and off the ribosome

measured by 19F NMR (mean ± SEM propagated from NMR line shape fits). (G) Thermodynamic parameters estimated from the nonlinear fits in panel F (mean ± SD). FLN5 F672A and FLN5 Δ6 have

indistinguishable thermodynamics, validating 672A as a pseudo wild-type system. (H) Nonlinear fit to a modified Gibbs-Helmholtz equation of the equilibrium constants (all constants relative

to the unfolded state) on and off the ribosome measured by 19F NMR (mean ± SEM propagated from NMR line shape fits). (I) Thermodynamic parameters estimated from the nonlinear fits in panel H

(mean ± SD). (J) Transverse relaxation rate (R2) measurements of isolated full-length (FL) FLN5 labelled at position 655 with tfmF recorded at a 19F-Larmor frequency of 470 MHz and 298 K.

(K) 1D 19F NMR spectra of isolated, full-length FLN5 in different concentrations of glycerol, fitted spectra in blue, raw spectra in grey. (L) Fitting of R2 rates for FL-FLN5 in different

concentrations of glycerol. (M) Correlation between measured R2 rates (panel L) and those obtained from the linewidths of the peaks in the 1D spectra (panel K). Points are shown as the mean 

± SEM propagated from NMR line shape fits. (N) Correlation between the 19F linewidth/R2 rate obtained from line shape fitting (mean ± SEM) and previously determined rotational correlation

times of FLN5 in different concentrations of glycerol25. (O) 1D 19F NMR spectrum of FLN5 + 47 used in panel (P). (P) Estimated populations of coTF intermediates I1 and I2 bound to the

ribosome based on the experimental 19F linewidth at 298 K6 and linear correlation between linewidth and rotational correlation time (panel N). The ribosome-bound populations were estimated

with an \({S}_{{bound}}^{2}=1.0\) (_τ__R,bound_ = 3003 ns) and are shown as the mean ± SEM propagated from fitted NMR linewidths. Source data EXTENDED DATA FIG. 9 CO- AND POST-TRANSLATIONAL

FOLDING THERMODYNAMICS OF I27 AND HRAS. (A) 19F NMR spectra of isolated titin I27 (F73A variant), (B) titin I27 + 34 RNC, (C) titin I27 + 34 W34E RNC (a fully unfolded variant37) and (D)

HRAS1-81 on the ribosome recorded at different temperatures (at a 19F-Larmor frequency of 470 MHz). (E) The linewidths of all four states in the wild-type and unfolded state of the mutant

I27 + 34 RNC are shown as the mean ± SEM from fitted NMR lineshapes. (F) 19F NMR spectrum of HRAS1-81 on the ribosome with two destabilising mutations V8E/V14E recorded at 298 K and a

19F-Larmor frequency of 470 MHz. Analysis of the NMR data in the time domain (as described in ref. 6) shows that the fit is better for a single state compared to two states for the mutant

(BIC = 6,897 and BIC = 6,894, respectively). Wild-type HRAS1-81 fits better to two states than a single state (BIC = 17,900 and BIC = 17,721, respectively). The right panel shows the

linewidths of the two states in wild-type HRAS1-81 (Fig. 4d) and the mutant shown here. The bars represent the mean ± SEM from fitted NMR lineshapes. (G) HRAS GDP/GTP nucleotide exchange

assay (schematic on top shows exchange from GDP- to GTP-bound state for RNC, released (control) and refolded HRAS). The plot shows the GDP/GTP exchange activity (mean ± SEM) from three

independent refolding reactions (n = 3). We measured the activity as the maximum signal/noise fluorescence ratio obtained relative to buffer (see Methods). Values of ≤ 1 signify no activity.

(H) Pulse proteolysis experiments of refolded and native (control) HRAS. The proteolytic stability of HRAS was assayed with thermolysin (see schematic on top). Exemplar western blots are

shown and densitometry analyses from three independent refolding repeats (n = 3) are globally fit to an exponential decay with the obtained degradation rate indicated on the plot (mean ± SD

from fitted parameters are shown). See Supplementary Fig. 6 for uncropped gel images. (I) Pulse proteolysis experiments (with thermolysin) of refolded (R) and native (control, C) HRAS in

rabbit reticulocyte lysate (RRL). Exemplar western blots are shown comparing relative refolded/GDP band intensities at 0 and 9 h time points. Densitometry analyses (mean ± SEM) with n = 3

for the 0, 2 and 5 h time points and n = 2 refolding reactions for the 9 h time point are shown in the bottom bar plot. See Supplementary Fig. 7 for uncropped gel images. (J) 1H-15N

SOFAST-HMQC NMR spectra of refolded and native (control) HRAS for two independent refolding reactions (left and right, recorded at 298 K and 700 and 800 MHz, respectively). The chemical

shift perturbations (CSPs) and signal intensities (mean ± RMSE obtained from spectral noise) of refolded relative to native HRAS are shown below the spectra. The shaded grey areas highlight

switch regions 1 and 2, respectively, and the relative signal intensities are also coloured on the HRAS structure (PDB 4Q21). Source data EXTENDED DATA FIG. 10 NMR ANALYSES OF DESTABILISING

FLN5 MUTANTS ON AND OFF THE RIBOSOME. All data were recorded at a 1H-Larmor frequency of 500 MHz (19F-Larmor frequency of 470 MHz), 298 K. (A) Mutations mapped on the structure of FLN593.

(B) 19F NMR spectra of wild-type and mutant FLN5 RNCs. The spectrum of FLN5 + 34 P742A was previously reported6. (C) 19F NMR spectra of wild-type and four mutant FLN5 RNCs in the presence of

2.5 M Urea. The spectral noise was used to estimate the maximum population of the native state to calculate a lower bound of its folding free energy in urea. (D) 19F NMR translational

diffusion experiment on FLN5 + 67 672 A RNC in 2.5 M urea to monitor the integrity of the sample in urea. The diffusion coefficient does not change significantly throughout the course of the

NMR experiment and is consistent with a ribosome-bound species6. (E) 19F NMR spectra of the FLN5 + 34 RNC in 1.5 M urea at different temperatures recorded at a 19F-Larmor frequency of 470 

MHz. Raw spectra are shown in grey, lineshape fits in colour and the total fit in black. Residuals after fitting are shown below each spectrum. (F) Nonlinear fits to a modified

Gibbs-Helmholtz equation for FLN5 + 34 in 1.5 M urea and isolated FLN5Δ6 as a reference. Values are shown as the mean ± SEM propagated from NMR line shape fits. (G) The resulting

thermodynamic parameters including the ones of FLN5 + 34 without urea (−urea) for reference are shown as mean ± SD obtained from the fits. (H) 19F NMR spectra of wild-type and mutant FLN5 in

isolation. Stabilities were quantified from the unfolded and folded state populations under native conditions, and where 3.5 M urea was used to quantify the stability of less destabilising

variants relative to wild-type (assuming a constant m-value7). (I) 1H-15N SOFAST-HMQC spectra of mutant FLN5 variants in isolation (purple) overlaid with wild-type (black). The chemical

shift perturbations (CSPs) are mapped onto the crystal structure of FLN5. The thermodynamic stability and CSPs of isolated FLN5 variants P742A and E6 were previously reported and

characterised7,24. Source data SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Description of additional analyses as supplementary notes, including methodological background and quality

control for PRE-NMR experiments, comparison of molecular dynamics force fields, validation of molecular dynamics simulations against experimental data, convergence of molecular dynamics

simulations, and a description of additional energetic analyses. The Supplementary Information also contains supplementary tables and figures. REPORTING SUMMARY PEER REVIEW FILE SOURCE DATA

SOURCE DATA FIG. 1 SOURCE DATA FIG. 2 SOURCE DATA FIG. 3 SOURCE DATA FIG. 4 SOURCE DATA FIG. 5 SOURCE DATA EXTENDED DATA FIG. 1 SOURCE DATA EXTENDED DATA FIG. 2 SOURCE DATA EXTENDED DATA

FIG. 3 SOURCE DATA EXTENDED DATA FIG. 4 SOURCE DATA EXTENDED DATA FIG. 5 SOURCE DATA EXTENDED DATA FIG. 6 SOURCE DATA EXTENDED DATA FIG. 7 SOURCE DATA EXTENDED DATA FIG. 8 SOURCE DATA

EXTENDED DATA FIG. 9 SOURCE DATA EXTENDED DATA FIG. 10 RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Streit, J.O., Bukvin, I.V., Chan, S.H.S. _et al._ The ribosome lowers the entropic penalty of protein folding. _Nature_ 633, 232–239

(2024). https://doi.org/10.1038/s41586-024-07784-4 Download citation * Received: 10 August 2023 * Accepted: 04 July 2024 * Published: 07 August 2024 * Issue Date: 05 September 2024 * DOI:

https://doi.org/10.1038/s41586-024-07784-4 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative