Particle–hole symmetry protects spin-valley blockade in graphene quantum dots

ABSTRACT Particle–hole symmetry plays an important role in the characterization of topological phases in solid-state systems1. It is found, for example, in free-fermion systems at half

filling and it is closely related to the notion of antiparticles in relativistic field theories2. In the low-energy limit, graphene is a prime example of a gapless particle–hole symmetric

system described by an effective Dirac equation3,4 in which topological phases can be understood by studying ways to open a gap by preserving (or breaking) symmetries5,6. An important

example is the intrinsic Kane–Mele spin-orbit gap of graphene, which leads to a lifting of the spin-valley degeneracy and renders graphene a topological insulator in a quantum spin Hall

phase7 while preserving particle–hole symmetry. Here we show that bilayer graphene allows the realization of electron–hole double quantum dots that exhibit near-perfect particle–hole

symmetry, in which transport occurs via the creation and annihilation of single electron–hole pairs with opposite quantum numbers. Moreover, we show that particle–hole symmetric spin and

valley textures lead to a protected single-particle spin-valley blockade. The latter will allow robust spin-to-charge and valley-to-charge conversion, which are essential for the operation

of spin and valley qubits. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your

institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $29.99 / 30 days cancel any time Learn more Subscribe to this journal

Receive 51 print issues and online access $199.00 per year only $3.90 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may

be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support

SIMILAR CONTENT BEING VIEWED BY OTHERS SPIN-VALLEY COUPLING IN SINGLE-ELECTRON BILAYER GRAPHENE QUANTUM DOTS Article Open access 02 September 2021 KONDO EFFECT AND SPIN–ORBIT COUPLING IN

GRAPHENE QUANTUM DOTS Article Open access 14 October 2021 SPIN SKYRMION GAPS AS SIGNATURES OF STRONG-COUPLING INSULATORS IN MAGIC-ANGLE TWISTED BILAYER GRAPHENE Article Open access 21

October 2023 DATA AVAILABILITY The data supporting the findings are available in a Zenodo repository under accession code https://doi.org/10.5281/zenodo.7821944. CODE AVAILABILITY The

simulation code is available in a Zenodo repository under accession code https://doi.org/10.5281/zenodo.7821944 REFERENCES * Zirnbauer, M. R. Particle-hole symmetries in condensed matter.

_J. Math. Phys._ 62, 021101 (2021). Article  ADS  MathSciNet  MATH  Google Scholar  * Maurice, D. P. A. A theory of electrons and protons. _Proc. R. Soc. Lond. A Math. Phys. Sci._ 126,

360–365 (1930). MATH  Google Scholar  * McCann, E. & Koshino, M. The electronic properties of bilayer graphene. _Rep. Prog. Phys._ 76, 056503 (2013). Article  ADS  PubMed  Google Scholar

  * Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. _Rev. Mod. Phys._ 81, 109–162 (2009). Article  ADS  CAS  Google

Scholar  * Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the “parity anomaly”. _Phys. Rev. Lett._ 61, 2015–2018 (1988). Article 

ADS  MathSciNet  CAS  PubMed  Google Scholar  * Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. _Rev. Mod. Phys._ 83, 1057–1110 (2011). Article  ADS  CAS  Google

Scholar  * Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. _Phys. Rev. Lett._ 95, 226801 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Konschuh, S., Gmitra, M.,

Kochan, D. & Fabian, J. Theory of spin-orbit coupling in bilayer graphene. _Phys. Rev. B_ 85, 115423 (2012). Article  ADS  Google Scholar  * Kurzmann, A. et al. Kondo effect and

spin-orbit coupling in graphene quantum dots. _Nat. Commun._ 12, 6004 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Banszerus, L. et al. Spin-valley coupling in

single-electron bilayer graphene quantum dots. _Nat. Commun._ 12, 5250 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Wojtaszek, M., Vera-Marun, I. J., Whiteway, E.,

Hilke, M. & van Wees, B. J. Absence of hyperfine effects in 13C-graphene spin-valve devices. _Phys. Rev. B_ 89, 035417 (2014). Article  ADS  Google Scholar  * Fischer, J. & Loss, D.

Dealing with decoherence. _Science_ 324, 1277–1278 (2009). Article  CAS  PubMed  Google Scholar  * Icking, E. et al. Transport spectroscopy of ultraclean tunable band gaps in bilayer

graphene. _Adv. Electron. Mater._ 8, 2200510 (2022). Article  CAS  Google Scholar  * Eich, M. et al. Coupled quantum dots in bilayer graphene. _Nano Lett._ 18, 5042–5048 (2018). Article  ADS

  CAS  PubMed  Google Scholar  * Banszerus, L. et al. Electron-hole crossover in gate-controlled bilayer graphene quantum dots. _Nano Lett._ 20, 7709–7715 (2020). Article  ADS  CAS  PubMed 

PubMed Central  Google Scholar  * Banszerus, L. et al. Gate-defined electron-hole double dots in bilayer graphene. _Nano Lett._ 18, 4785–4790 (2018). Article  ADS  CAS  PubMed  Google

Scholar  * Banszerus, L. et al. Single-electron double quantum dots in bilayer graphene. _Nano Lett._ 20, 2005–2011 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Tong, C. et al.

Tunable valley splitting and bipolar operation in graphene quantum dots. _Nano Lett._ 21, 1068–1073 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Knothe, A. & Fal’ko, V. Influence

of minivalleys and Berry curvature on electrostatically induced quantum wires in gapped bilayer graphene. _Phys. Rev. B_ 98, 155435 (2018). Article  ADS  CAS  Google Scholar  * Laird, E. A.

et al. Quantum transport in carbon nanotubes. _Rev. Mod. Phys._ 87, 703–764 (2015). Article  ADS  MathSciNet  CAS  Google Scholar  * Banszerus, L. et al. Tunable interdot coupling in

few-electron bilayer graphene double quantum dots. _Appl. Phys. Lett._ 118, 103101 (2021). Article  ADS  CAS  Google Scholar  * Banszerus, L. et al. Observation of the spin-orbit gap in

bilayer graphene by one-dimensional ballistic transport. _Phys. Rev. Lett._ 124, 177701 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Johnson, A. C., Petta, J. R., Marcus, C. M.,

Hanson, M. P. & Gossard, A. C. Singlet-triplet spin blockade and charge sensing in a few-electron double quantum dot. _Phys. Rev. B_ 72, 165308 (2005). Article  ADS  Google Scholar  *

Borselli, M. G. et al. Pauli spin blockade in undoped Si/SiGe two-electron double quantum dots. _Appl. Phys. Lett._ 99, 063109 (2011). Article  ADS  Google Scholar  * Tong, C. et al. Pauli

blockade of tunable two-electron spin and valley states in graphene quantum dots. _Phys. Rev. Lett._ 128, 067702 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Bonet, E., Deshmukh, M.

M. & Ralph, D. C. Solving rate equations for electron tunneling via discrete quantum states. _Phys. Rev. B_ 65, 045317 (2002). Article  ADS  Google Scholar  * Möller, S. et al. Probing

two-electron multiplets in bilayer graphene quantum dots. _Phys. Rev. Lett._ 127, 256802 (2021). Article  ADS  PubMed  Google Scholar  * Sichau, J. et al. Resonance microwave measurements of

an intrinsic spin-orbit coupling gap in graphene: a possible indication of a topological state. _Phys. Rev. Lett._ 122, 046403 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Lyon, T.

J. et al. Probing electron spin resonance in monolayer graphene. _Phys. Rev. Lett._ 119, 066802 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Trauzettel, B., Bulaev, D. V., Loss, D.

& Burkard, G. Spin qubits in graphene quantum dots. _Nat. Phys._ 3, 192–196 (2007). Article  CAS  Google Scholar  * Koppens, F. H. L. et al. Driven coherent oscillations of a single

electron spin in a quantum dot. _Nature_ 442, 766–771 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise

and fidelity higher than 99.9%. _Nat. Nanotechnol._ 13, 102–106 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Philips, S. G. J. et al. Universal control of a six-qubit quantum

processor in silicon. _Nature_ 609, 919–924 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Sousa de Almeida, A. J. et al. Ambipolar charge sensing of few-charge quantum

dots. _Phys. Rev. B_ 101, 201301 (2020). Article  ADS  CAS  Google Scholar  * Bandurin, D. A. et al. Resonant terahertz detection using graphene plasmons. _Nat. Commun._ 9, 5392 (2018).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Bordoloi, A., Zannier, V., Sorba, L., Schönenberger, C. & Baumgartner, A. Spin cross-correlation experiments in an electron

entangler. _Nature_ 612, 454–458 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Wang, G. et al. Singlet and triplet Cooper pair splitting in hybrid superconducting nanowires. _Nature_

612, 448–453 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Tan, Z. B. et al. Cooper pair splitting by means of graphene quantum dots. _Phys. Rev. Lett._ 114, 096602 (2015). Article 

ADS  CAS  PubMed  Google Scholar  * Leijnse, M. & Flensberg, K. Parity qubits and poor man’s Majorana bound states in double quantum dots. _Phys. Rev. B_ 86, 134528 (2012). Article  ADS

  Google Scholar  * Dvir, T. et al. Realization of a minimal Kitaev chain in coupled quantum dots. _Nature_ 614, 445–450 (2023). Article  ADS  CAS  PubMed  Google Scholar  * Knothe, A.,

Glazman, L. I. & Fal’ko, V. I. Tunneling theory for a bilayer graphene quantum dot’s single- and two-electron states. _New J. Phys._ 24, 043003 (2022). Article  ADS  MathSciNet  Google

Scholar  * Banszerus, L. et al. Pulsed-gate spectroscopy of single-electron spin states in bilayer graphene quantum dots. _Phys. Rev. B_ 103, L081404 (2021). Article  ADS  CAS  Google

Scholar  * Banszerus, L. et al. Dispersive sensing of charge states in a bilayer graphene quantum dot. _Appl. Phys. Lett._ 118, 093104 (2021). Article  ADS  CAS  Google Scholar  * Kurzmann,

A. et al. Excited states in bilayer graphene quantum dots. _Phys. Rev. Lett._ 123, 026803 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Thess, A. et al. Crystalline ropes of metallic

carbon nanotubes. _Science_ 273, 483–487 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Lee, Y. et al. Tunable valley splitting due to topological orbital magnetic moment in bilayer

graphene quantum point contacts. _Phys. Rev. Lett._ 124, 126802 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Knothe, A. & Fal’ko, V. Quartet states in two-electron quantum dots

in bilayer graphene. _Phys. Rev. B_ 101, 235423 (2020). Article  ADS  CAS  Google Scholar  * Island, J. O. et al. Spin-orbit-driven band inversion in bilayer graphene by the van der Waals

proximity effect. _Nature_ 571, 85–89 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Gmitra, M. & Fabian, J. Proximity effects in bilayer graphene on monolayer WSe2: field-effect

spin valley locking, spin-orbit valve, and spin transistor. _Phys. Rev. Lett._ 119, 146401 (2017). Article  ADS  PubMed  Google Scholar  * Shchepetilnikov, A. V., Nefyodov, Y. A., Kukushkin,

I. V. & Dietsche, W. Electron g-factor in GaAs/AlGaAs quantum wells of different width and barrier Al concentrations. _J. Phys. Conf. Ser._ 456, 012035 (2013). Article  CAS  Google

Scholar  * Giorgioni, A., Paleari, S., Cecchi, S., Vitiello, E. & Pezzoli, F. Strong confinement-induced engineering of the g factor and lifetime of conduction electron spins in Ge

quantum wells. _Nat. Commun._ 7, 13886 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Yang, C. H. et al. Spin-valley lifetimes in a silicon quantum dot with tunable

valley splitting. _Nat. Commun._ 4, 2069 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Hendrickx, N. W. et al. A single-hole spin qubit. _Nat. Commun._ 11, 3478 (2020). Article  ADS 

CAS  PubMed  PubMed Central  Google Scholar  * Albrecht, W., Moers, J. & Hermanns, B. HNF – Helmholtz Nano Facility. _J. Large Scale Res. Facil._ 3, 112 (2017). Article  Google Scholar 

Download references ACKNOWLEDGEMENTS We thank H. Bluhm, K. Flensberg, F. Haupt and L. Schreiber for helpful discussions, and F. Lentz, S. Trellenkamp and D. Neumaier for help with sample

fabrication. This project received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 881603 (Graphene Flagship); from the European

Research Council (grant agreement no. 820254) from Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy—Cluster of Excellence Matter and Light for Quantum Computing (ML4Q) EXC

2004/1 0 390534769, through DFG (STA 1146/11-1); and from the Helmholtz Nano Facility54. K.W. and T.T. acknowledge support from JSPS KAKENHI (grant nos. 19H05790, 20H00354 and 21H05233).

AUTHOR INFORMATION Author notes * These authors contributed equally: L. Banszerus and S. Möller AUTHORS AND AFFILIATIONS * JARA-FIT and 2nd Institute of Physics A, RWTH Aachen University,

Aachen, Germany L. Banszerus, S. Möller, K. Hecker, E. Icking, C. Volk & C. Stampfer * Peter Grünberg Institute (PGI-9), Forschungszentrum Jülich, Jülich, Germany L. Banszerus, S.

Möller, K. Hecker, E. Icking, C. Volk & C. Stampfer * Research Center for Functional Materials, National Institute for Materials Science, Tsukuba, Japan K. Watanabe * International

Center for Materials Nanoarchitectonics, National Institute for Materials Science, Tsukuba, Japan T. Taniguchi * JARA-Institute for Quantum Information, RWTH Aachen University, Aachen,

Germany F. Hassler Authors * L. Banszerus View author publications You can also search for this author inPubMed Google Scholar * S. Möller View author publications You can also search for

this author inPubMed Google Scholar * K. Hecker View author publications You can also search for this author inPubMed Google Scholar * E. Icking View author publications You can also search

for this author inPubMed Google Scholar * K. Watanabe View author publications You can also search for this author inPubMed Google Scholar * T. Taniguchi View author publications You can

also search for this author inPubMed Google Scholar * F. Hassler View author publications You can also search for this author inPubMed Google Scholar * C. Volk View author publications You

can also search for this author inPubMed Google Scholar * C. Stampfer View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS L.B., C.V. and C.S.

conceived the experiment. L.B., S.M., K.H. and E.I. fabricated the device. L.B., S.M. and C.V. performed measurements and analysed data. S.M. and F.H. performed simulations of the current.

K.W. and T.T. synthesized hBN crystals. C.V. and C.S. supervised the project. L.B., S.M., C.V., F.H. and C.S. wrote the manuscript with contributions from all authors. L.B. and S.M.

contributed equally to this work. CORRESPONDING AUTHOR Correspondence to C. Stampfer. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER

REVIEW INFORMATION _Nature_ thanks Ivan Borzenets, Patrik Recher and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are

available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. EXTENDED DATA

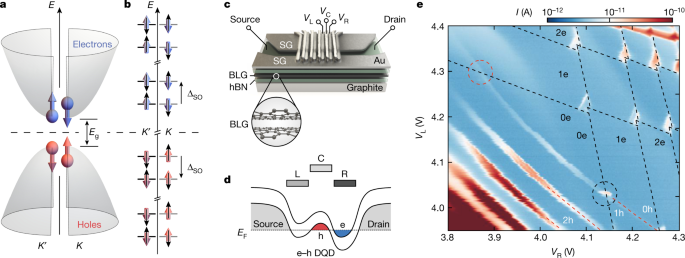
FIGURES AND TABLES EXTENDED DATA FIG. 1 CHARGE STABILITY DIAGRAMS FOR OPPOSITE BIAS VOLTAGES IN DQD #1. A,B, Charge stability diagrams of DQD #1 (as in Fig. 1d) measured at a bias voltage of

_V_SD = 1 mV (A) and _V_SD = −1 mV (B) (_T_ = 10 mK). The dashed circles mark the formation of single electron – single hole DQDs using the hole QD and an electron QD to the left (DQD #3,

red) or right (DQD #1, black) of the hole QD. C,D, Schematics of the valence and conduction band edge profiles along the p-type channel. An electron-hole double quantum dot is formed using

the hole QD and the electron QD underneath the left (right) FG (see red (black) circles in Extended Data Figs. 1a,b). EXTENDED DATA FIG. 2 EXTRACTING ΔSO FROM MEASUREMENTS ON A

SINGLE-ELECTRON DQD IN THE SAME DEVICE. A, Charge stability diagrams of the (1_e_, 0_e_) ↔ (0_e_, 1_e_) transition of an electron-electron DQD measured at _V_SD = 1 mV and _B_⊥ = 0 T (_T_ = 

10 mK). A ground state and an excited state transition are visible (see black arrows). B, Cut along the yellow dashed line in A. Two Lorentzian peaks (dashed lines) are fitted to the data.

Inset, schematic energy diagrams of an electron-electron DQD in the finite bias regime for different interdot detuning energies _ε_, illustrating resonant transport from the left (L) to the

right (R) QD through the ground state of each QD (transition (i)) and resonant transport at _ε_ = ΔSO (transition (ii)). Data taken from ref. 10. EXTENDED DATA FIG. 3 ADDITIONAL DATA SET FOR

ANOTHER ELECTRON-HOLE DOUBLE QUANTUM DOT (DQD #2) IN THE SAME DEVICE. A,B, Gate configurations used to form the DQDs #1, #3 and #2 in the device, respectively. C, Charge stability diagram

of an e-h DQD formed with the second set of gate fingers (DQD #2, see panel b). The dashed circle marks the (0_h_, 0_e_) → (1_h_, 1_e_) transition. _V_SD = 1 mV (_T_ = 10 mK). D,E, Close-ups

of the (0_h_, 0_e_) → (1_h_, 1_e_) triple point measured at _V_SD = 0.5 mV and _V_SD = 1.5 mV, respectively. Transport only occurs via the _α_ and _β_ transition. F, Charge stability

diagram as in panel E measured at _B_⊥ = 0.6 T. G, Charge stability diagram as in panel E at _B_∥ = 0.7 T. H,I, Charge stability diagrams as in panels D,E at _V_SD = − 0.5 mV and _V_SD = 

−1.5 mV. Transport is strongly suppressed; only co-tunnelling can be observed. J,K, Charge stability diagrams as in panels F,G measured at _B_⊥ = 0.6 T and _B_∥ = 0.7 T and _V_SD = −1.5 mV.

EXTENDED DATA FIG. 4 PROBING THE SINGLE-PARTICLE PARTICLE-HOLE SYMMETRIC SPECTRUM. A, Energy dispersion of single-particle states in the first orbital for electrons and holes as a function

of in-plane (_B_∥, left) and out-of-plane (_B_⊥, right) magnetic fields. States and transitions are labelled as in Fig. 3a. B, Current through DQD #2 as a function of the detuning energy

\(\widetilde{\varepsilon }\) (see yellow dashed line in Extended Data Fig. 3e) and _B_⊥ at _V_SD = 1.5 mV. The white dashed line marks the onset of the bias transport window. C, Current

through the device as a function of \(\widetilde{\varepsilon }\) and _B_∥ at _V_SD = 1.5 mV. D,E, Data acquired in the blockade regime (_V_SD = −1.5 mV). The current has been measured as a

function of _B_⊥ and _B_∥, respectively. Data have been symmetrized around _B_ = 0. EXTENDED DATA FIG. 5 CHARGE STABILITY DIAGRAMS OF THE FIRST TRIPLE POINT SIMULATED BY SOLVING THE RATE

EQUATION. A–C, The forward bias direction (_V_SD = 1 mV) for different magnetic fields, showing the same features as the experimental data presented in Fig. 2. D–F, The blocked bias

direction (_V_SD = − 1 mV) for the same magnetic fields. For zero magnetic field, the blockade is lifted at the corners of the bias triangle, where back and forth tunneling to source (or

drain) allows lifting the blockade. The effect is even larger at finite parallel magnetic fields, where the spins are tilted into the plane of the BLG. EXTENDED DATA FIG. 6 COMPARISON OF THE

SINGLE PARTICLE ELECTRON-HOLE BLOCKADE AND SINGLET-TRIPLET PAULI BLOCKADE. A,B, Schematic of the chemical potentials in an electron-hole DQD for A _ϵ_ = 0 and B _ϵ_ = Δorb. For clearity the

energy axis of the schematic is drawn to scale, such that _E_g = 10Δorb = 100ΔSO. It can be seen that the band gap energy protects the blockade to be lifted by detuning. C,D, The same

configurations in a unipolar DQD in (1,1) → (2,0) configuration. The singlet-triplet splitting ΔS-T is chosen to be equal to the orbital splitting Δorb in A,B. Is can be seen that the

blockade is lifted as soon as _ϵ_ = ΔS-T. Additionally, it can be lifted by relaxation of the triplet (1,1) state into the singlet (1,1) state. EXTENDED DATA FIG. 7 TRANSPORT PROPERTIES

SIMULATED FOR ASYMMETRIC VALLEY G-FACTORS IN THE ELECTRON AND HOLE QDS. A–H, Calculation of the current through the device as a function of the detuning energy \(\widetilde{\varepsilon }\)

(see arrow in Fig. 2c) and perpendicular magnetic field at a finite bias of _V_SD = 2 mV (A–D) and _V_SD = −2 mV (E–H). In A, the valley g-factors of the two QDs are chosen asymmetrically

(\({g}_{{\rm{v}}}^{{\rm{e}}}=15\) for the electron QD and \({g}_{{\rm{v}}}^{{\rm{h}}}=20\) for the hole QD), resulting in a splitting of both, the _α_ and _β_ transition, which scales with

the difference in the valley g-factors. In B, the valley g-factors of the two QDs are chosen less asymmetrically (\({g}_{{\rm{v}}}^{{\rm{e}}}=15\) for the electron QD and

\({g}_{{\rm{v}}}^{{\rm{h}}}=17\) for the hole QD), resulting in a smaller splitting of both, the _α_ and _β_ transition, which scales with the difference in the valley g-factors. In C the

valley g-factors are chosen symmetrically (_g_v = 15), and no dependence on _B_⊥ is observed. In D, the experimentally observed g-factor difference of \({g}_{{\rm{v}}}^{{\rm{e}}}=15\) and

\({g}_{{\rm{v}}}^{{\rm{h}}}=15.1\) is used for the simulation. E–H, For reverse bias, the single-particle blockade remains robust and the current is zero, independent of the chosen valley

g-factor asymmetry, as the spin and valley texture, that is, the level ordering remains symmetrical. EXTENDED DATA FIG. 8 DETERMINING THE G-FACTOR ASYMMETRY. A, Exemplary line trace of the

tunnelling current at _B_⊥ = 0 as a function of the detuning. The sum of two Gauss curves with width Γ is fitted to the data (see dashed line). B, Γ extracted from the line fits as shown in

A, as a function of _B_⊥. Attributing the linear broadening of _α_ and _β_ to an asymmetry of valley g-factors between electron and hole QD yields Δ_g_ ≈ 0.11. SUPPLEMENTARY INFORMATION PEER

REVIEW FILE RIGHTS AND PERMISSIONS Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s)

or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Banszerus, L., Möller, S., Hecker, K. _et al._ Particle–hole symmetry protects spin-valley blockade in graphene quantum dots. _Nature_

618, 51–56 (2023). https://doi.org/10.1038/s41586-023-05953-5 Download citation * Received: 30 September 2022 * Accepted: 14 March 2023 * Published: 03 May 2023 * Issue Date: 01 June 2023 *

DOI: https://doi.org/10.1038/s41586-023-05953-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is

not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative