Experimental observation of vortex rings in a bulk magnet

Letter Published: 30 November 2020 Experimental observation of vortex rings in a bulk magnet Claire Donnelly  ORCID: orcid.org/0000-0002-9942-24191,2,3, Konstantin L. Metlov  ORCID:

orcid.org/0000-0002-3929-56654,5, Valerio Scagnoli  ORCID: orcid.org/0000-0002-8116-88702,3, Manuel Guizar-Sicairos  ORCID: orcid.org/0000-0002-8293-36343, Mirko Holler3, Nicholas S.

Bingham2,3, Jörg Raabe  ORCID: orcid.org/0000-0002-2071-68963, Laura J. Heyderman  ORCID: orcid.org/0000-0003-3843-66112,3, Nigel R. Cooper  ORCID: orcid.org/0000-0002-4662-12541 &

…Sebastian Gliga  ORCID: orcid.org/0000-0003-1729-10703 Show authors Nature Physics volume 17, pages 316–321 (2021)Cite this article

7523 Accesses

131 Altmetric

Metrics details

Vortex rings are remarkably stable structures that occur in a large variety of systems, such as in turbulent gases (where they are at the origin of weather phenomena)1, fluids (with

implications for biology)2, electromagnetic discharges3 and plasmas4. Although vortex rings have also been predicted to exist in ferromagnets5, they have not yet been observed. Using X-ray

magnetic nanotomography6, we imaged three-dimensional structures forming closed vortex loops in a bulk micromagnet. The cross-section of these loops consists of a vortex–antivortex pair and,

on the basis of magnetic vorticity (a quantity analogous to hydrodynamic vorticity), we identify these configurations as magnetic vortex rings. Although such structures have been predicted

to exist as transient states in exchange ferromagnets5, the vortex rings we observe exist as static configurations, and we attribute their stability to the dipolar interaction. In addition,

we observe stable vortex loops intersected by point singularities7 at which the magnetization within the vortex and antivortex cores reverses. We gain insight into the stability of these

states through field and thermal equilibration protocols. The observation of stable magnetic vortex rings opens up possibilities for further studies of complex three-dimensional solitons in

bulk magnets, enabling the development of applications based on three-dimensional magnetic structures.

Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution

options: Log in Learn about institutional subscriptions Read our FAQs Contact customer support Fig. 1: Measuring and reconstructing the magnetic structure and magnetic vorticity within a

GdCo2 pillar.Fig. 2: Structure of a vortex ring with circulating magnetic vorticity.Fig. 3: Structure of a vortex loop containing magnetization singularities.Fig. 4: Magnetic vorticity plots

measured for a similar micropillar at remanence showing the effect of different field histories. Similar content being viewed by others Controlled creation and decay of singly-quantized

vortices in a polar magnetic phase Article Open access 12 March 2021 Vortex phases and glassy dynamics in the highly anisotropic superconductor HgBa2CuO4+δ Article Open access 24 June 2020

Vortex confinement through an unquantized magnetic flux Article Open access 06 September 2024 Data availability

Experimental data and analysis codes used for this manuscript can be found at https://doi.org/10.5281/zenodo.4041745.

References Yao, J. & Lundgren, T. Experimental investigation of microbursts. Exp. Fluids 21, 17–25 (1996).

Article  Google Scholar 

Kilner, P. J. et al. Asymmetric redirection of flow through the heart. Nature 404, 759–761 (2000).

Article  Google Scholar 

Stenhoff, M. Ball Lightning: An Unsolved Problem in Atmospheric Physics 1st edn (Springer, 1999).

Akhmetov, D. G. Vortex Rings 1st edn (Springer, 2009).

Cooper, N. R. Propagating magnetic vortex rings in ferromagnets. Phys. Rev. Lett. 82, 1554–1557 (1999).

Article  ADS  Google Scholar 

Donnelly, C. et al. Three-dimensional magnetization structures revealed with X-ray vector nanotomography. Nature 547, 328–331 (2017).

Article  ADS  Google Scholar 

Feldtkeller, E. Mikromagnetisch Stetige und unstetige Magnetisierungskonfigurationen. Zeitschrift. Angew. Phys. 19, 530–536 (1965).

Google Scholar 

Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).

Article  ADS  Google Scholar 

Wachowiak, A. et al. Direct observation of internal spin structure of magnetic vortex cores. Science 298, 577–580 (2002).

Article  ADS  Google Scholar 

Guslienko, K. Magnetic vortex state stability reversal and dynamics in restricted geometries. J. Nanosci. Nanotechnol. 8, 2745–2760 (2008).

Article  Google Scholar 

Choe, S.-B. et al. Vortex core-driven magnetization dynamics. Science 304, 420–422 (2004).

Article  ADS  Google Scholar 

Van Waeyenberge, B. et al. Magnetic vortex core reversal by excitation with short bursts of an alternating field. Nature 444, 461–464 (2006).

Article  ADS  Google Scholar 

Hertel, R., Gliga, S., Fähnle, M. & Schneider, C. M. Ultrafast nanomagnetic toggle switching of vortex cores. Phys. Rev. Lett. 98, 117201 (2007).

Article  ADS  Google Scholar 

Pigeau, B. et al. A frequency-controlled magnetic vortex memory. Appl. Phys. Lett. 96, 132506 (2010).

Article  ADS  Google Scholar 

Hertel, R. & Schneider, C. M. Exchange explosions: magnetization dynamics during vortex–antivortex annihilation. Phys. Rev. Lett. 97, 177202 (2006).

Article  ADS  Google Scholar 

Gliga, S., Yan, M., Hertel, R. & Schneider, C. M. Ultrafast dynamics of a magnetic antivortex: micromagnetic simulations. Phys. Rev. B 77, 060404 (2008).

Article  ADS  Google Scholar 

Gliga, S., Hertel, R. & Schneider, C. M. Switching a magnetic antivortex core with ultrashort field pulses. J. Appl. Phys. 103, 07B115 (2008).

Article  Google Scholar 

Neudert, A. et al. Bloch-line generation in cross-tie walls by fast magnetic-field pulses. J. Appl. Phys. 99, 08F302 (2006).

Article  Google Scholar 

Papanicolaou, N. in Singularities in Fluids, Plasmas and Optics Vol. 404 (ASI Series C404, NATO, 1993).

Belavin, A. A. & Polyakov, A. M. Metastable states of two-dimensional isotropic ferromagnet. ZETP Lett. 22, 245–247 (1975).

ADS  Google Scholar 

Senthil, T., Vishwanath, A., Balents, L., Sachdev, S. & Fisher, M. P. A. Deconfined quantum critical points. Science 303, 1490–1494 (2004).

Article  ADS  Google Scholar 

Ackerman, P. J. & Smalyukh, I. I. Diversity of knot solitons in liquid crystals manifested by linking of preimages in torons and hopfions. Phys. Rev. X 7, 011006 (2017).

Google Scholar 

Donnelly, C. et al. High-resolution hard X-ray magnetic imaging with dichroic ptychography. Phys. Rev. B 94, 064421 (2016).

Article  ADS  Google Scholar 

Donnelly, C. et al. Tomographic reconstruction of a three-dimensional magnetization vector field. New J. Phys. 20, 083009 (2018).

Article  ADS  Google Scholar 

Chikazumi, S. in International Series of Monographs on Physics 2nd edn, Vol. 94 (Oxford Univ. Press, 2010).

Arrott, A., Heinrich, B. & Aharoni, A. Point singularities and magnetization reversal in ideally soft ferromagnetic cylinders. IEEE Trans. Magn. 15, 1228–1235 (1979).

Article  ADS  Google Scholar 

Ackerman, P. J. & Smalyukh, I. I. Static three-dimensional topological solitons in fluid chiral ferromagnets and colloids. Nat. Mater. 16, 426–432 (2016).

Article  ADS  Google Scholar 

Lee, T. & Pang, Y. Nontopological solitons. Phys. Rep. 221, 251–350 (1992).

Article  MathSciNet  Google Scholar 

Malozemoff, A. & Slonczewski, J. in Magnetic Domain Walls in Bubble Materials (eds Malozemoff, A. & Slonczewski, J.) Ch. IV, 77–121 (Academic Press, 1979).

Miltat, J. & Thiaville, A. Vortex cores—smaller than small. Science 298, 555–555 (2002).

Article  Google Scholar 

Kerr, R. M. & Brandenburg, A. Evidence for a singularity in ideal magnetohydrodynamics: implications for fast reconnection. Phys. Rev. Lett. 83, 1155–1158 (1999).

Article  ADS  Google Scholar 

Smalyukh, I. I., Lansac, Y., Clark, N. A. & Trivedi, R. P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids.

Nat. Mater. 9, 139–145 (2009).

Article  ADS  Google Scholar 

Kim, D.-H. et al. Bulk Dzyaloshinskii–Moriya interaction in amorphous ferrimagnetic alloys. Nat. Mater. 18, 685–690 (2019).

Article  ADS  Google Scholar 

Liu, Y., Lake, R. K. & Zang, J. Binding a hopfion in a chiral magnet nanodisk. Phys. Rev. B 98, 174437 (2018).

Article  ADS  Google Scholar 

Sutcliffe, P. Hopfions in chiral magnets. J. Phys. A 51, 375401 (2018).

Article  MATH  Google Scholar 

Tai, J.-S. B. & Smalyukh, I. I. Static Hopf solitons and knotted emergent fields in solid-state noncentrosymmetric magnetic nanostructures. Phys. Rev. Lett. 121, 187201 (2018).

Article  ADS  Google Scholar 

Chen, B. G.-G, Ackerman, P. J., Alexander, G. P., Kamien, R. D. & Smalyukh, I. I. Generating the Hopf fibration experimentally in nematic liquid crystals. Phys. Rev. Lett. 110, 237801

(2013).

Article  ADS  Google Scholar 

Donnelly, C. et al. Time-resolved imaging of three-dimensional nanoscale magnetisation dynamics. Nat. Nanotechnol. 15, 356–360 (2020).

Article  ADS  Google Scholar 

Pokrovskii, V. L. & Uimin, G. V. Dynamics of vortex pairs in a two-dimensional magnetic material. JETP Lett. 41, 128 (1985).

ADS  Google Scholar 

Papanicolaou, N. & Spathis, P. N. Semitopological solitons in planar ferromagnets. Nonlinearity 12, 285–302 (1999).

Article  ADS  MathSciNet  MATH  Google Scholar 

Cooper, N. R. Solitary waves of planar ferromagnets and the breakdown of the spin-polarized quantum Hall effect. Phys. Rev. Lett. 80, 4554–4557 (1998).

Article  ADS  Google Scholar 

Huang, Y., Kang, W., Zhang, X., Zhou, Y. & Zhao, W. Magnetic skyrmion-based synaptic devices. Nanotechnology 28, 08LT02 (2017).

Article  Google Scholar 

Fernández-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).

Article  ADS  Google Scholar 

Holler, M. et al. OMNY PIN—a versatile sample holder for tomographic measurements at room and cryogenic temperatures. Rev. Sci. Instrum. 88, 113701 (2017).

Article  ADS  Google Scholar 

Holler, M. et al. High-resolution non-destructive three-dimensional imaging of integrated circuits. Nature 543, 402–406 (2017).

Article  ADS  Google Scholar 

Pfeiffer, F. X-ray ptychography. Nat. Photon. 12, 9–17 (2017).

Article  ADS  Google Scholar 

Rodenburg, J. M. et al. Hard-X-ray lensless imaging of extended objects. Phys. Rev. Lett. 98, 034801 (2007).

Article  ADS  Google Scholar 

Wakonig, K. et al. PtychoShelves, a versatile high-level framework for high-performance analysis of ptychographic data. J. Appl. Crystallogr. 53, 574–586 (2020).

Article  Google Scholar 

Scagnoli, V. et al. Linear polarization scans for resonant X-ray diffraction with a double-phase-plate configuration. J. Synch. Radiat. 16, 778–787 (2009).

Article  Google Scholar 

Donnelly, C. Hard X-ray Tomography of Three Dimensional Magnetic Structures. PhD thesis, ETH Zurich (2017).

van Heel, M. & Schatz, M. Fourier shell correlation threshold criteria. J. Struct. Biol. 151, 250–262 (2005).

Article  Google Scholar 

Ahrens, J., Geveci, B. & Law, C. ParaView: An End-User Tool for Large Data Visualization. Visualisation Handbook (Elsevier, 2005).

Wilczek, F. & Zee, A. Linking numbers, spin and statistics of solitons. Phys. Rev. Lett. 51, 2250–2252 (1983).

Article  ADS  MathSciNet  Google Scholar 

Gross, D. J. Meron configurations in the two-dimensional O(3) σ-model. Nucl. Phys. B 132, 439–456 (1978).

Article  ADS  MathSciNet  Google Scholar 

Usov, N. A. & Peschany, S. E. Magnetization curling in a fine cylindrical particle. J. Magn. Magn. Mater. 118, L290–L294 (1993).

Article  ADS  Google Scholar 

Huber, E. E., Smith, D. O. & Goodenough, J. B. Domain-wall structure in permalloy films. J. Appl. Phys. 29, 294–295 (1958).

Article  ADS  Google Scholar 

Metlov, K. L. Simple analytical description of the cross-tie domain wall structure. Appl. Phys. Lett. 79, 2609–2611 (2001).

Article  ADS  Google Scholar 

Download references

X-ray magnetic tomography measurements were performed at the cSAXS beamline at the Swiss Light Source, Paul Scherrer Institute (PSI), Switzerland, and X-ray microcrystallography measurements

at the X06DA beamline at the Swiss Light Source, PSI, Switzerland. We thank A. Bogatyrëv for his careful reading of the manuscript and valuable remarks, R. Cowburn for discussions and V.

Olieric for microcrystallography measurements. We thank R. M. Galera for providing and performing magnetic characterizations of the GdCo2 nugget, S. Stutz for the sample fabrication and E.

Müller from the Electron Microscopy Facility at PSI for the focused ion beam preparation of the pillar samples. C.D. is supported by the Leverhulme Trust (ECF-2018-016), the Isaac Newton

Trust (18-08) and the L’Oréal-UNESCO UK and Ireland Fellowship for Women in Science. S.G. was funded by the Swiss National Science Foundation, Spark project no. 190736. K.L.M. acknowledges

the support of the Russian Science Foundation under project no. RSF 16-11-10349. N.R.C. was supported by EPSRC grant EP/P034616/1 and by a Simons Investigator Award.

Author informationAuthors and Affiliations Cavendish Laboratory, University of Cambridge, Cambridge, UK

Claire Donnelly & Nigel R. Cooper

Laboratory for Mesoscopic Systems, Department of Materials, ETH Zürich, Zürich, Switzerland

Claire Donnelly, Valerio Scagnoli, Nicholas S. Bingham & Laura J. Heyderman

Paul Scherrer Institute, Villigen, Switzerland

Claire Donnelly, Valerio Scagnoli, Manuel Guizar-Sicairos, Mirko Holler, Nicholas S. Bingham, Jörg Raabe, Laura J. Heyderman & Sebastian Gliga

Donetsk Institute for Physics and Engineering, Donetsk, Ukraine

Konstantin L. Metlov

Institute for Numerical Mathematics RAS, Moscow, Russia

Konstantin L. Metlov

AuthorsClaire DonnellyView author publications You can also search for this author inPubMed Google Scholar

Konstantin L. MetlovView author publications You can also search for this author inPubMed Google Scholar

Valerio ScagnoliView author publications You can also search for this author inPubMed Google Scholar

Manuel Guizar-SicairosView author publications You can also search for this author inPubMed Google Scholar

Mirko HollerView author publications You can also search for this author inPubMed Google Scholar

Nicholas S. BinghamView author publications You can also search for this author inPubMed Google Scholar

Jörg RaabeView author publications You can also search for this author inPubMed Google Scholar

Laura J. HeydermanView author publications You can also search for this author inPubMed Google Scholar

Nigel R. CooperView author publications You can also search for this author inPubMed Google Scholar

Sebastian GligaView author publications You can also search for this author inPubMed Google Scholar

The study of topological magnetic features in three dimensions was conceived by S.G., C.D. and K.L.M., and originated from a larger project on 3D magnetic systems conceived by L.J.H. and

J.R. C.D., M.G.-S., S.G., V.S., M.H. and J.R. performed the experiments. Magnetometry measurements of the material were performed by N.S.B. and V.S. C.D. performed the magnetic

reconstruction with support from M.G.-S. and V.S. C.D. analysed the data and N.R.C. conceived the calculation of the magnetic vorticity. C.D., K.L.M., N.R.C. and S.G. interpreted the

magnetic configuration. K.L.M. developed the analytical model. C.D., K.L.M., N.R.C. and S.G. wrote the manuscript with contributions from all authors.

Corresponding authors Correspondence to Claire Donnelly, Konstantin L. Metlov or Sebastian Gliga.

The authors declare no competing interests.

Peer review information Nature Physics thanks Paul Sutcliffe and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

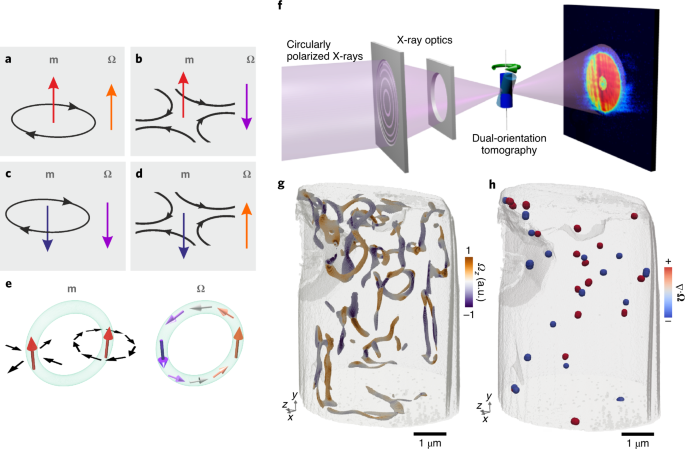
of the vortex ring with circulating magnetic vorticity (presented in Fig. 2), shown in successive slices through the loop.

The magnetization within each slice is represented by the streamlines. The colourscale in the top row indicates the \(\hat{x}\) component of the magnetization, while the colour scale in the

bottom row indicates the \(\hat{x}\) component of the vorticity. The vorticity associated with the vortex structure extending throughout the pillar changes sign in slice d due to the

presence of a Bloch point, while the vortex–antivortex pair conserves its vorticity throughout. In slices b and c, the magnetization forms a structure similar to that of a cross-tie wall,

which dissolves as the pair unwinds, at slices a and d, resulting in a single vortex.

Top, middle and bottom rows: Magnetization, pre-images and vorticity distribution for the different 2+1 dimensional analytical models. The magnetization plots (top row) only include the

projection of the magnetization onto the shown plane, while the rings correspond to the positions of the vortex and antivortex centres. The colour indicates the mz component of the

magnetization. The pre-images are shown as volumes where the magnetization vectors deviate only slightly from certain directions di, indicated by the colour-coded arrows on each

corresponding sphere. The opacity and colour on the vorticity plots indicate the magnitude of local vorticity vectors. The structure in c is comparable to the vortex rings in Fig. 2, while

the structure in d is comparable to that in Fig. 3.

successive slices through the loop.

The magnetization within each slice is represented by the streamlines. The colour scale in the top row indicates the \(\hat{x}\) component of the magnetization, while the colourscale in the

bottom row indicates the \(\hat{x}\) component of the vorticity. The vorticity along the vortex core reverses between slices b and c, while the vorticity along the antivortex core reverses

between slices c and d. f, The white isosurface, plotted along with the vortex loop, corresponds to mx=0 and separates regions of mx=+1 and mx=−1, thus highlighting the presence of a

complicated domain wall structure. The Bloch points are located at the intersection of the loop with this isosurface (locations indicated by the dashed circles).

vortex loop containing magnetization singularities (presented in Fig. 3) seen from multiple directions.

The vortex loop containing Bloch points is plotted using the isosurfaces mx= ± 1 (a,c) and pre-images (b,d). In a and b, the vortex loop and its pre-images have the same spatial orientation

as in Fig. 3a. In c and d, the loop and pre-images are presented with the same orientation as in Fig. 3g.

presence and distribution of regions of high magnetic vorticity, and magnetization singularities.

a,c, Vorticity distribution following the application of a 7 T saturating field (a) and following saturation and field cooling (c). b, Regions of high divergence of the magnetic vorticity

indicate the presence of Bloch points (red) and anti-Bloch points (blue) at remanence, following saturation. d, In the same way, singularities are identified after heating at 400 K and field

cooling in a 7 T field. Noticeably fewer magnetic structures with high vorticity are present following the field-cooling procedure.

GdCo2 pillar.

The substructure of the Bragg peaks, magnified in the inset to the right, indicates the polycrystalline nature of the material.

following the two different protocols.

The position of the central vortex core is plotted using red and blue isosurfaces for the remanent magnetic structure after (red) the application of a 7 T magnetic field, and after (blue)

the application of the field-cooling protocol. After both protocols, the vortex core occupies almost the same position.

Rights and permissions Reprints and permissions

About this articleCite this article Donnelly, C., Metlov, K.L., Scagnoli, V. et al. Experimental observation of vortex rings in a bulk magnet. Nat. Phys. 17, 316–321 (2021).

https://doi.org/10.1038/s41567-020-01057-3

Download citation

Received: 03 April 2020

Accepted: 07 September 2020

Published: 30 November 2020

Issue Date: March 2021

DOI: https://doi.org/10.1038/s41567-020-01057-3

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative