Anomalous josephson coupling and high-harmonics in non-centrosymmetric superconductors with s-wave spin-triplet pairing

ABSTRACT We study the Josephson effects arising in junctions made of non-centrosymmetric superconductors with spin-triplet pairing having _s_-wave orbital-singlet symmetry. We demonstrate

that the orbital dependent character of the spin-triplet order parameter determines its non-trivial texture in the momentum space due to the inversion symmetry breaking and spin-orbit

interactions. The emergence of this pattern is responsible for the occurrence of an anomalous Josephson coupling and a dominance of high-harmonics in the current phase relation. Remarkably,

due to the spin-orbital couplings, variations in the electronic structure across the heterostructure can generally turn the ground state of the junction from 0- to a generic value of the

Josephson phase, thus realizing the so-called _φ_-junction. Hallmarks of the resulting Josephson behavior, apart from non-standard current-phase relation, are provided by an unconventional

temperature and magnetic field dependence of the critical current. These findings indicate the path for the design of superconducting orbitronics devices and account for several observed

anomalies of the supercurrent in oxide interface superconductors. SIMILAR CONTENT BEING VIEWED BY OTHERS LARGE JOSEPHSON CURRENT IN WEYL NODAL LOOP SEMIMETALS DUE TO ODD-FREQUENCY

SUPERCONDUCTIVITY Article Open access 25 June 2020 EXTREMELY LONG-RANGE, HIGH-TEMPERATURE JOSEPHSON COUPLING ACROSS A HALF-METALLIC FERROMAGNET Article 02 December 2021 JOSEPHSON DIODE

EFFECT FROM COOPER PAIR MOMENTUM IN A TOPOLOGICAL SEMIMETAL Article Open access 15 August 2022 INTRODUCTION In the presence of conventional Cooper pairing the current-phase relation (CPR) of

a superconductor-insulator-superconductor junction is given by \({I}_{J}={I}_{c}\sin (\phi )\)1, with _I__c_ being the critical current and _ϕ_ the phase difference. While the sinusoidal

shape is not always preserved2, as in extended superconductor-normal metal-superconductor junction or narrow ballistic weak links3,4,5,6,7, a vanishing supercurrent and non-degenerate

minimum of the Josephson energy at _ϕ_ = 0 are robust marks of the CPR in conventional Josephson junctions (JJ). In this context, progress in materials science and nanofabrication have led

to several physical cases with an unconventional CPR. Deviations from standard CPR indeed can manifest as a Josephson energy offset of a fractional flux quantum, leading to the so called

_φ_0-junction8,9,10,11,12,13,14,15,16,17,18 that violates time-reversal symmetry. On the other hand, for an offset of half-integer flux quantum a _π_-junction19 is realized. Apart from

anomalous phase shifts, the energy of the Josephson junction can keep the symmetry of phase-inversion but exhibits a minimum at values of the phase which is different from 0 or _π_, setting

out a _φ_-Josephson junction. Typical requirements to achieve a _φ_-junction are (i) combination of 0- and _π_- Josephson couplings20,21,22,23,24, (ii) specific parameters range and

geometric configuration of the junction25,26,27,28, or (iii) higher harmonics20. Observations of CPR in form of _φ_0 or _φ_-junctions as well as 0-_π_ transitions have been reported in a

variety of devices based on InSb nanowires29, ferromagnetic heterostructures23,30, superconducting spin valves31,32, and junctions with superconducting materials having non-trivial gap

symmetry (e.g., iron picnitides33, oxides interface34,35, and cuprates25,26,36). Here, competing 0- and _π_-Josephson channels lead to a vanishing first harmonic with a consequent dominant

role of the second harmonic in determining the Josephson CPR. Having a CPR with non-negligible harmonics higher than the second one is however quite unusual and difficult to achieve without

fine tuning. Recently, the combination of inversion symmetry breaking and multiple orbital degrees of freedom has emerged as an innovative route to tailor unconventional Josephson effects.

This is mostly due to the expectation in acentric materials of a superconducting order parameter that goes beyond the canonical singlet-triplet mixed parity37, as for the inter-band

anti-phase pairing (e.g., _s_+− and _s_+−−)38,39 or pure even-parity inter-orbital spin-triplet pairs40. Striking experimental evidences of anomalous Josephson effects and supercurrents have

been indeed reported in noncentrosymmetric superconductors based on oxides interface34,35,41 which have been ascribed to the occurrence of competing 0- and _π_-Josephson channels as well as

to second harmonics in the CPR. The microscopic origin of the observed effects is however not yet fully settled. Motivated by this challenge and, in general, by the origin of anomalous

Josephson effects in low-dimensional non-centrosymmetric superconductors (NCSs), we demonstrate how to achieve 0-, _π_- and _φ_- Josephson couplings together with robust high-harmonics in

Josephson junction by exploiting multi-orbital degrees of freedom. In spin-triplet superconductors the Cooper pairs are typically described by the so-called D-vector whose components express

the amplitude of the zero spin projection of the spin-triplet pairing states42. Here, we find that the Josephson effects are a striking manifestation of the non-trivial orientations of the

D-vector in momentum space arising from the intertwining of its orbital dependent character with the inversion symmetry breaking and spin-orbit couplings. We demonstrate that 0 to _π_

transitions and _φ_-Josephson phase can be generally realized and manipulated by varying the character of the electronic structure and the strength of inversion symmetry breaking

interaction, thus being highly tunable through gating or electric field. Hallmarks of a Josephson junction based on this type of NCSs are: (i) CPR with _φ_-phase and dominant high-harmonics,

(ii) anomalous temperature dependence of the critical current with a linear upturn at low temperature and (iii) maximum of the critical current at finite applied magnetic field in the

Fraunhofer pattern. We discuss how this type of pairing can account for the recent observations on supercurrents behavior in oxides interface superconductors34,35. RESULTS ORBITAL-SINGLET

SPIN-TRIPLET PAIRS AND _D_-VECTOR PROFILE ALONG THE FERMI LINES We consider a multi-orbital 2D electronic system with spin-triplet _s_-wave pairing. In the normal state we have three bands

arising from atomic orbitals spanning an _L_ = 1 angular momentum subspace, such as _d__a_ orbitals with _a_ = (_y__z_, _z__x_, _x__y_). Here, we refer to _d_-orbitals localized at the site

of a square lattice assuming a _C_4_v_ point group symmetry. The breaking of mirror symmetry, in the plane of the junction, sets out a polar axis _z_ leading to an orbital Rashba interaction

(_α_OR) that couples the atomic angular momentum L with the crystal wave-vector K in the standard form \(\sim [{\hat{L}}_{x}\sin ({k}_{y})-{\hat{L}}_{y}\sin ({k}_{x})]\)39,43,44,45,46. The

atomic spin-orbit coupling (_λ_SO) expresses the interaction between the spin and angular momentum at each site. Taking the basis of the local creation operator of electrons of _d_-orbitals,

\({\hat{C}}_{{{{\boldsymbol{k}}}}}^{{\dagger} }=[{c}_{yz,\uparrow {{{\boldsymbol{k}}}}}^{{\dagger} },{c}_{zx,\uparrow {{{\boldsymbol{k}}}}}^{{\dagger} },{c}_{xy,\uparrow

{{{\boldsymbol{k}}}}}^{{\dagger} },{c}_{yz,\downarrow {{{\boldsymbol{k}}}}}^{{\dagger} },{c}_{zx,\downarrow {{{\boldsymbol{k}}}}}^{{\dagger} },{c}_{xy,\downarrow

{{{\boldsymbol{k}}}}}^{{\dagger} }]\), the Hamiltonian can be generally expressed as

$$\hat{{{{\mathcal{H}}}}}=\mathop{\sum}\limits_{{{{\boldsymbol{k}}}}}{\hat{C}}_{{{{\boldsymbol{k}}}}}^{{\dagger} }\hat{H}({{{\boldsymbol{k}}}}){\hat{C}}_{{{{\boldsymbol{k}}}}},$$ (1) whose

details of the matrix structure and the electronic dispersion with nearest-neighbor hoppings are provided in the Methods. In the superconducting state, the Bogoliubov-de Gennes (BdG)

Hamiltonian is then directly constructed by including the pair potential \(\hat{{{\Delta }}}({{{\boldsymbol{k}}}})\). In the present study, our focus is on the symmetry allowed local

(_s_-wave) spin-triplet pairing with orbital-singlet character and B1 symmetry in the _C_4_v_ group. This type of pairing is energetically favorable when considering that inter-orbital

interactions are dominant with respect to the intra-orbital ones40. The B1 order parameter is described40,47,48 by a _K_-independent D-vector with _d__x_ (_d__y_) components corresponding to

local electron pairs between {_d__z__x_, _d__x__y_} ({_d__z__y_, _d__x__y_}) orbitals, respectively. By introducing orbital indices to label the D-vector, we have that

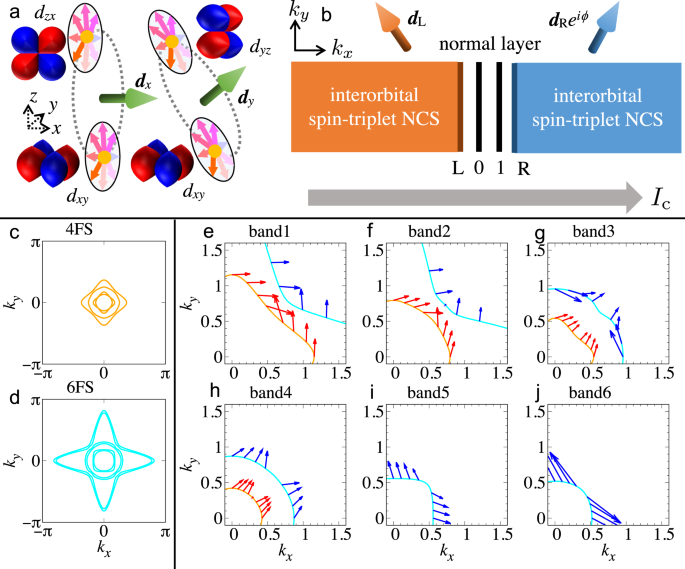
\({d}_{x}^{(xy,zx)}={d}_{y}^{(xy,yz)}\). A schematic illustration of the spin and orbital structure of the Cooper pair is shown in Fig. 1a. This type of pairing exhibits nodal points along

the diagonal of the Brillouin zone ([110] direction) with nonzero topological number that is due to the chiral symmetry of the BdG Hamiltonian40,47,48,49,50,51,52. Before analysing the

Josephson effects in the junction formed by interfacing NCS [Fig. 1b], it is useful to consider the structure of the spin-triplet pairing in momentum space along the Fermi lines. This is

evaluated by considering the anomalous components of the Green’s function (see Methods for details). To this aim we choose two representative configurations whose electron density yields

four [Fig. 1c] and six [Fig. 1d] Fermi lines around the Γ point. The inner Fermi lines are more isotropic, while the outer ones exhibit a more pronounced anisotropy. For the examined 2D

tetragonal configuration, the _x__y_ orbital at _k_ = 0 is lower in energy as compared to the (_z__x_, _y__z_) bands. We start by observing how the orientation of the D-vector at a given

_K_-point is modified along the Fermi lines. For those bands having large Fermi momentum, i.e., bands 1 and 2 in Fig. 1e, f, we have obtained that the D-vector is mostly pointing along the

_x_ (_y_) direction for crystal wave vectors above (below) the diagonal. This is because the electronic configurations at the Fermi level have dominant _x__y_ character and mixing with

_z__x_ and _y__z_ states through the spin-orbit and the orbital Rashba couplings. When we consider the bands closer to the center of the Brillouin zone (Fig. 1g–j), we observe that the

D-vector exhibits a completely different pattern which is marked by an orientation that is mostly along the [110] direction (Fig. 1g, h) or perpendicular to it (Fig. 1i, j). Such behavior is

mostly due to the dominant (_z__x_, _y__z_) character of the electronic states and the fact that the B1 pairing does not involve a direct coupling between such orbital states, thus implying

an equal weight for _d__x_ and _d__y_ components. The results in Fig. 1c–j provide evidence of the Cooper pairs along the Fermi lines having a spin-triplet configuration not uniform in

orientation and amplitude that strongly depends on the orbital character of the corresponding electronic states. MISALIGNMENT OF _D_-VECTORS ACROSS THE INTERFACE AND 0-_Φ_ JOSEPHSON COUPLING

Let us now consider the Josephson current in the NCS-NCS junction. For the computation of the Josephson current, we adopt the recursive Green’s function method53,54 assuming two

semi-infinite superconductors and setting the pair potential in the Josephson junction as \({\hat{{{\Delta }}}}_{{{{\rm{L}}}}}={\hat{{{\Delta }}}}_{{{{\rm{B1}}}}}\) and \({\hat{{{\Delta

}}}}_{{{{\rm{R}}}}}={\hat{{{\Delta }}}}_{{{{\rm{B1}}}}}{e}^{i\phi }\), with _ϕ_ being the phase difference between the superconductors forming the junction (Fig. 1b). Below the critical

temperature _T_c, Josephson current _I_c(_ϕ_) at the temperature _T_ is then determined48,55 as $${I}_{{{{\rm{c}}}}}(\phi )=-\frac{ie{k}_{{{{\rm{B}}}}}T}{\hslash }\int\nolimits_{-\pi }^{\pi

}d{k}_{y}{{{\rm{Tr}}}}^{\prime} \mathop{\sum}\limits_{i{\varepsilon }_{n}}[{\tilde{t}}_{{{{\rm{N}}}}}^{{\dagger} }{\hat{G}}_{01}({k}_{y},i{\varepsilon }_{n},\phi

)-{\tilde{t}}_{{{{\rm{N}}}}}{\hat{G}}_{10}({k}_{y},i{\varepsilon }_{n},\phi )],$$ (2) with \({\tilde{t}}_{{{{\rm{N}}}}}\) being the nearest-neighbor hopping matrix in the normal layer, the

non-local Green’s functions \({\hat{G}}_{01}({k}_{y},i{\varepsilon }_{n},\phi )\) and \({\hat{G}}_{10}({k}_{y},i{\varepsilon }_{n},\phi )\) (Fig. 1b and Methods), and the fermionic Matsubara

frequency _i__ε__n_ = _i_(2_n_ + 1)_π__k_B_T_. Here, \({{{\rm{Tr}}}}^{\prime}\) means that the trace is only in the electron space. Having demonstrated that the D-vector has a non-trivial

texture along the Fermi lines, we expect that the relative orientation of D-vectors in the two sides of the junction has a key role in setting out the Josephson effect. To this aim we employ

two representative D-vectors configurations with a distribution of misalignment angles _γ_ that can be ~0 or close to _π_/2. The D-vector along the four Fermi lines of the left (L) NCS

(Fig. 2a) and right (R) NCS (Fig. 2b) is evaluated by considering different values for the electron filling via _μ_, and the spin-orbital couplings through _α_OR and _λ_SO (Supplementary

Figs. 1, 2, 3). Here, we focus on the region of momentum space where the left- and right-side Fermi lines mostly overlap. We start considering electronic configurations that result into

D-vectors that are about collinear on the two sides of the junction (Fig. 2c). Hence, taking into account those spin-triplet tunneling processes, we find that the derivative of Josephson

current is positive at low _ϕ_ and the CPR has a standard profile with maximum at about _ϕ_ ~ _π_/2 (Fig. 2d). Next, as reported in Fig. 2e–g, the texture of D-vector in the region nearby

the diagonal of the Brillouin zone at the crossings of the left- and right-side Fermi lines indicate that the misalignment angle is about _π_/2. On the other hand, for momentum along the

[100] or [010] directions, the D-vectors are mostly aligned. In this case, the resulting Josephson current [Fig. 2h] is marked by a change of sign in the derivative of Josephson current at

low _ϕ_ together with vanishing critical current for _ϕ_ different from the time-reversal points at _ϕ_ = 0 or _π_. This implies that the ground state realizes the so called _φ_-Josephson

configuration. By tuning the amplitude of the orbital Rashba coupling or of the spin-orbit interaction it is possible to induce 0 to _π_ Josephson phases and observe CPR dominated by

harmonics higher than the second one close to the critical points (Figs. S2, S3 in the Supplementary Information). To understand these Josephson effects, we recall that as shown in ref. 56

for a specific geometrical design of the junction, the Josephson current _J_(_ϕ_) between spin-triplet superconductors marked by D-vectors that are misaligned by an angle _γ_ is expressed as

$$J(\phi )\propto \frac{\sin (\phi +\gamma )}{\sqrt{1-| {Z}_{t}{| }^{2}{\sin }^{2}\left(\frac{\phi +\gamma }{2}\right)}}+\frac{\sin (\phi -\gamma )}{\sqrt{1-| {Z}_{t}{| }^{2}{\sin

}^{2}\left(\frac{\phi -\gamma }{2}\right)}}$$ (3) with _ϕ_ being the applied phase difference and _Z__t_ the transmission amplitude across the junction. This expression indicates that in the

tunneling process the spin-triplet pairs with opposite spin polarization undergo an antiphase shift to keep the time-reversal symmetry with an amount that is proportional to the

misalignment angle _γ_. Here, it is immediate to deduce that for a value of _γ_ that is about _π_/2, the current _J_(_ϕ_) at small phase difference can change sign, thus turning the

Josephson phase behavior from 0 to _π_. Since for the examined NCS-NCS junction the D-vector has a variation of the orientation in the momentum space, it is useful to consider the Josephson

behavior resulting from the superposition of different misaligned D-vectors. Taking the representative case of a pair of Josephson channels with different configurations of D-vector

misalignment, as in Fig. 3a, b, one can find that when the angles _γ_ and _γ_1 are both close to _π_/2, the resulting current is marked by non-vanishing and comparable amplitude of the first

four harmonics (i.e. _I_1,_I_2,_I_3,_I_4). In this case, the CPR has a profile that yields a _φ_-Josephson coupling. Another peculiar hallmark of the Josephson current in the examined

NCS-NCS junction is represented by the occurrence of high-harmonics in the CPR with nonvanishing and comparable amplitude. We find that this behavior can be also ascribed to the nontrivial

misalignment of the D-vectors across the junction and the superposition of different configurations along the Fermi lines. Indeed, let us consider the Josephson current obtained by summing

up only two channels (Fig. 3b), one with a given misalignment angle (_γ_1) and the other one (_γ_) to vary in the range [ − _π_, _π_] (Fig. 3c). Within this effective description, we find

that high-harmonics generally occur in the CPR (Fig. 3d). The CPR has an anomalous profile with a positive derivative at low _ϕ_ and multiple oscillations due to the competing high

harmonics. Since the D-vector texture is not homogeneous along the Fermi lines, it is natural to expect that various channels with inequivalent mismatch angles and transmission amplitudes

cooperate to build up such behavior for the supercurrent. In Fig. 3e, f, we provide evidence of the CPR for the NCS-NCS junction, whose profile is significantly marked by high-harmonics at

low temperature which in turn tend to get suppressed by increasing the temperature towards the transition into the normal state. Finally, we evaluate the response to an applied magnetic

field that acts to modulate the critical current amplitude (details in the Supplementary Information). We find that the resulting Fraunhofer pattern (Fig. 3i, j), as a consequence of the

intrinsic competing 0 and _π_ Josephson couplings, does not have a maximum at zero magnetic flux, as expected in conventional spin-singlet JJ. Interestingly, even for a CPR with a

0-Josephson coupling, as in Fig. 3i, the critical current has a local minimum rather than a maximum at zero applied magnetic field (Fig. 3i, j). This demonstrates that the intrinsic tendency

of having competing Josephson channels in the case of NCS superconductors with _s_-wave orbital-singlet and spin-triplet pairing has clearcut and detectable signatures in the magnetic field

response. DISCUSSION We now discuss the impact of our findings in SrTiO3 based hetero-structures, such as LaAlO3/SrTiO3 (LAO-STO)57,58. The LAO-STO is an ideal 2D electron system with

non-centrosymmetric multi-orbital superconductivity38,40,59 exhibiting a remarkable control of the superconducting critical temperature by electrostatic gating60,61,62 together with Rashba

spin-orbit coupling63,64 and the occupation of the Ti 3d orbitals (_d__x__y_,_d__z__x_,_d__y__z_)65,66. The superconducting phase exhibits several anomalous properties that cannot be easily

addressed within a conventional spin-singlet scenario. Clearcut unconventional observations are provided by the superconducting gap suppression nearby the Lifshitz transition67,68, the

anomalous magnetic field dependence of critical current in weak links34,41 and uniform nanowires69, and several in-gap bound states probed by tunneling spectroscopy70. The significant role

of inhomogeneities also poses fundamental questions on the nature of the superconducting state in LAO-STO interface, excluding _p_-wave spin-triplet pairing as a candidate, and pointing to

an even-parity (_s_-wave) multi-band superconductivity which is robust to disorder. Recently, superconducting transport measurements in nano-devices34,35 have provided direct and significant

evidences of an orbital dependent unconventional pairing. The central experimental findings demonstrate: i) an anomalous enhancement of the critical current at weak applied magnetic field,

ii) an asymmetric response with respect to the magnetic field direction, and iii) the supercurrent anomalies are gate dependent, getting pronounced when reaching the Lifshitz transition at

the onset of the occupation of the (_d__z__x_,_d__y__z_) bands. In this context, our results can account for the central observations of the superconductng transport measurements. Our

analysis is based on planar 2D junctions as for the experimental configuration and the unveiled Josephson effect, due to the inter-orbital spin-triplet pairing, leads to _π_-phase and

high-harmonics in the Josephson current. As demonstrated by the analysis of the Fraunhofer pattern, the combination of _π_-phase and high-harmonics provides the enhancement of the critical

current at weak applied magnetic field and we find it to be robust with respect to variations of the electronic parameters in the two sides of the junction. This result can be particularly

relevant for the LAO-STO where the gating is related to an inhomogeneous distribution of the electron density in the 2D electron gas and of the inversion symmetry breaking at the interface.

Concerning the asymmetric response with respect to the magnetic field direction, our results indicate that the combination of _π_-phase and high-harmonics is not sufficient to yield the

effect. One has to consider it in a spatially inhomogeneous array of Josephson junctions35. Hence, we expect that the observed asymmetry of the Fraunhofer pattern with respect to the

magnetic field can be dependent on the spatially homogeneity of the superconductor in terms of granularity and inclusion of nanometric sized islands. Our findings highlight the relevant role

of _s_-wave inter-orbital spin-triplet pairing in noncentrosymmetric junctions for achieving competing 0- and _π_-Josephson couplings together with high-harmonics in the current phase

relation. Differently to single-band superconductors, the resulting CPR is tied to the character of the electronic structure and thus can be potentially tuned in a controlled way by changing

the electron density and the Rashba coupling through gating. This aspect has a direct impact on the transport properties of LAO-STO junctions and points to distinct design of Josephson

devices. We also point out that the distribution of the spin moment of the Cooper pairs in momentum space is a key quantum resource for the generation of CPR with dominance of

high-harmonics. Remarkably, in all these configurations the magnetic field response reveals a Fraunhofer pattern with a minimum of the critical current at vanishing field. While nonstandard

magneto-electric effects71,72,73,74 are based on the magnetic field tunability of the D-vector orientation52,71,75, our findings highlight the role of the orbital rather than the spin degree

of freedom. Hence, in perspective, due to the demonstrated intrinsic orbital tunability of the D-vector texture by orbital Rashba coupling, our findings set out innovative routes to design

orbitally driven magneto-electric effects and Josephson devices for superconducting orbitronics with orbital control of the supercurrent. METHODS MODEL The Hamiltonian in the normal state

\(\hat{H}({{{\boldsymbol{k}}}})\) is given by $$\hat{H}({{{\boldsymbol{k}}}})={\hat{H}}_{0}({{{\boldsymbol{k}}}})+{\hat{H}}_{{{{\rm{SO}}}}}+{\hat{H}}_{{{{\rm{is}}}}}({{{\boldsymbol{k}}}}).$$

(4) where \({\hat{H}}_{0}({{{\boldsymbol{k}}}})\) denotes the kinetic term, $$\hat{H}({{{\boldsymbol{k}}}})=\hat{\varepsilon }({{{\boldsymbol{k}}}})\otimes {\hat{\sigma }}_{0},$$ (5)

$$\hat{\varepsilon }({{{\boldsymbol{k}}}})=\left(\begin{array}{ccc}{\varepsilon }_{yz}({{{\boldsymbol{k}}}})&0&0\\ 0&{\varepsilon }_{zx}({{{\boldsymbol{k}}}})&0\\

0&0&{\varepsilon }_{xy}({{{\boldsymbol{k}}}})\end{array}\right),$$ (6) $${\varepsilon }_{yz}({{{\boldsymbol{k}}}})=2{t}_{1}(1-\cos {k}_{y})+2{t}_{3}(1-\cos {k}_{x}),$$ (7)

$${\varepsilon }_{zx}({{{\boldsymbol{k}}}})=2{t}_{1}(1-\cos {k}_{x})+2{t}_{3}(1-\cos {k}_{y}),$$ (8) $${\varepsilon }_{xy}({{{\boldsymbol{k}}}})=4{t}_{2}-2{t}_{2}(\cos {k}_{x}+\cos

{k}_{y})+{{{\Delta }}}_{{{{\rm{t}}}}}.$$ (9) \({\hat{H}}_{{{{\rm{SO}}}}}\) and \({\hat{H}}_{{{{\rm{is}}}}}({{{\boldsymbol{k}}}})\) stand for the atomic spin-orbit coupling and inversion

symmetry breaking terms, $${\hat{H}}_{{{{\rm{SO}}}}}={\lambda }_{{{{\rm{SO}}}}}\hat{{{{\boldsymbol{L}}}}}\cdot \hat{{{{\boldsymbol{\sigma }}}}},$$ (10)

$${\hat{H}}_{{{{\rm{is}}}}}({{{\boldsymbol{k}}}})={\alpha }_{{{{\rm{OR}}}}}[{\hat{L}}_{y}\sin {k}_{x}-{\hat{L}}_{x}\sin {k}_{y}],$$ (11) respectively. Here, \({\hat{\sigma }}_{i = 0,x,y,z}\)

denote the Pauli matrices in spin space and \({\hat{L}}_{j = 0,x,y,z}\) the _t_2_g_-orbital angular momentum operators projected onto _L_ = 2,

$${\hat{L}}_{x}=\left(\begin{array}{ccc}0&0&0\\ 0&0&i\\ 0&-i&0\end{array}\right),$$ (12) $${\hat{L}}_{y}=\left(\begin{array}{ccc}0&0&-i\\ 0&0&0\\

i&0&0\end{array}\right),$$ (13) $${\hat{L}}_{z}=\left(\begin{array}{ccc}0&i&0\\ -i&0&0\\ 0&0&0\end{array}\right),$$ (14) in the [_d__y__z_, _d__z__x_, 

_d__x__y_] basis. For the (100) oriented surface, the local term \(\tilde{u}({k}_{y})\) and nearest neighbor hopping matrix \(\tilde{t}({k}_{y})\) can be explicitly derived. The local term

\(\tilde{u}({k}_{y})\) is given by $$\tilde{u}({k}_{y})=\left(\begin{array}{cc}\hat{u}({k}_{y})&{\hat{{{\Delta }}}}_{{{{\rm{B1}}}}}\\ {\hat{{{\Delta }}}}_{{{{\rm{B1}}}}}^{{\dagger}

}&-{\hat{u}}^{* }(-{k}_{y})\end{array}\right),$$ (15) $$\hat{u}({k}_{y})={\hat{u}}_{0}({k}_{y})+{\hat{u}}_{{{{\rm{SO}}}}}+{\hat{u}}_{{{{\rm{is}}}}}({k}_{y}),$$ (16)

$${\hat{u}}_{0}({k}_{y})=\left(\begin{array}{ccc}{\tilde{\varepsilon }}_{yz}({k}_{y})&0&0\\ 0&{\tilde{\varepsilon }}_{zx}({k}_{y})&0\\ 0&0&{\tilde{\varepsilon

}}_{xy}({k}_{y})\end{array}\right)\otimes {\hat{\sigma }}_{0},$$ (17) $${\tilde{\varepsilon }}_{yz}({k}_{y})=2{t}_{1}(1-\cos {k}_{y})+2{t}_{3},$$ (18) $${\tilde{\varepsilon

}}_{zx}({k}_{y})=2{t}_{1}+2{t}_{3}(1-\cos {k}_{y}),$$ (19) $${\tilde{\varepsilon }}_{xy}({k}_{y})=4{t}_{2}-2{t}_{2}\cos {k}_{y}+{{{\Delta }}}_{{{{\rm{t}}}}},$$ (20)

$${\hat{u}}_{{{{\rm{SO}}}}}={\hat{H}}_{{{{\rm{SO}}}}},$$ (21) $${\hat{u}}_{{{{\rm{is}}}}}({k}_{y})=-{\alpha }_{{{{\rm{OR}}}}}{\hat{L}}_{x}\otimes \hat{{\sigma }_{0}}\sin {k}_{y},$$ (22) and

the nearest neighbor hopping \(\tilde{t}({k}_{y})\), $$\tilde{t}({k}_{y})=\left(\begin{array}{cc}\hat{t}({k}_{y})&0\\ 0&-{\hat{t}}^{* }(-{k}_{y})\end{array}\right),$$ (23)

$$\hat{t}({k}_{y})=\left(\begin{array}{ccc}-{t}_{3}&0&\frac{{\alpha }_{{{{\rm{OR}}}}}}{2}\\ 0&-{t}_{1}&0\\ -\frac{{\alpha

}_{{{{\rm{OR}}}}}}{2}&0&-{t}_{2}\end{array}\right)\otimes \hat{{\sigma }_{0}}.$$ (24) RECURSIVE GREEN FUNCTION METHOD In the superconducting state the Green’s function is expressed

as $$\tilde{G}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})=\frac{1}{i{\varepsilon

}_{n}-{\hat{H}}_{{{{\rm{BdG}}}}}({{{\boldsymbol{k}}}})}=\left(\begin{array}{cc}\hat{G}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})&\hat{F}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})\\

\bar{F}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})&\bar{G}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})\end{array}\right),$$ (25) with the anomalous Green’s function for the orbital indices

(_α_, _β_) which is given by $${\hat{F}}^{(\alpha ,\beta )}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})=\left(\begin{array}{cc}{F}_{\uparrow \uparrow }^{(\alpha ,\beta

)}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})&{F}_{\uparrow \downarrow }^{(\alpha ,\beta )}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})\\ {F}_{\downarrow \uparrow }^{(\alpha ,\beta

)}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})&{F}_{\downarrow \downarrow }^{(\alpha ,\beta )}({{{\boldsymbol{k}}}},i{\varepsilon }_{n})\end{array}\right).$$ (26) Since we consider the

interorbital even-frequency/spin-triplet/orbital-singlet/_s_-wave pair potential, we focus on the D-vector in this pair amplitude. We define the D-vector for the interorbital

even-frequency/spin-triplet/orbital-singlet/_s_-wave pair amplitude, $${{{{\boldsymbol{d}}}}}^{(\alpha ,\beta )}=({d}_{x}^{(\alpha ,\beta )},{d}_{y}^{(\alpha ,\beta )},{d}_{z}^{(\alpha

,\beta )}),$$ (27) $${d}_{x}^{(\alpha ,\beta )}=\frac{1}{2}\left[{F}_{\downarrow \downarrow }^{(\alpha ,\beta )}-{F}_{\uparrow \uparrow }^{(\alpha ,\beta )}\right],$$ (28) $${d}_{y}^{(\alpha

,\beta )}=\frac{1}{2i}\left[{F}_{\uparrow \downarrow }^{(\alpha ,\beta )}+{F}_{\downarrow \downarrow }^{(\alpha ,\beta )}\right],$$ (29) $${d}_{z}^{(\alpha ,\beta )}={F}_{\uparrow

\downarrow +\downarrow \uparrow }^{(\alpha ,\beta )},$$ (30) Then, we also define $${{{{\boldsymbol{d}}}}}^{(j)}=({d}_{x}^{(j)},{d}_{y}^{(j)},{d}_{z}^{(j)}),$$ (31)

$${d}_{x}^{(j)}={d}_{xj}^{(xy,yz)}+{d}_{xj}^{(xy,zx)},$$ (32) $${d}_{y}^{(j)}={d}_{yj}^{(xy,yz)}+{d}_{yj}^{(xy,zx)},$$ (33) $${d}_{z}^{(j)}={d}_{zj}^{(xy,yz)}+{d}_{zj}^{(xy,zx)},$$ (34) with

_j_ = _L_, _R_ superconductors, respectively. In the numerical calculation, both _D_(_L_) and _D_(_R_) are real number. Thus, the misalignment of D-vectors between two superconductors is

obtained by $$\gamma (a,b)={\theta }_{{{{\rm{R}}}}}(b)-{\theta }_{{{{\rm{L}}}}}(a),$$ (35) with \({\theta }_{j}(a)=\arg [{d}_{x}^{(j)}+i{d}_{y}^{(j)}]\) for the band indices _a_ and _b_.

Here, we report the main steps for the determination of the Josephson current by the recursive Green’s function method54. $${\tilde{u}}_{{{{\rm{L}}}}}({k}_{y})=-{\mu

}_{{{{\rm{L}}}}}{\hat{L}}_{0}\otimes {\hat{\sigma }}_{0}+\tilde{u}({k}_{y}),$$ (36) $${\tilde{t}}_{{{{\rm{L}}}}}=\tilde{t}({k}_{y}),$$ (37) $${\tilde{u}}_{{{{\rm{R}}}}}({k}_{y})=-{\mu

}_{{{{\rm{R}}}}}{\hat{L}}_{0}\otimes {\hat{\sigma }}_{0}+\tilde{u}({k}_{y}),$$ (38) $${\tilde{t}}_{{{{\rm{R}}}}}=\tilde{t}({k}_{y}),$$ (39) $${\tilde{u}}_{{{{\rm{N}}}}}({k}_{y})=-{\mu

}_{{{{\rm{N}}}}}{\hat{L}}_{0}\otimes {\hat{\sigma }}_{0}+\left(\begin{array}{cc}\hat{u}({k}_{y})&0\\ 0&-{\hat{u}}^{* }(-{k}_{y})\end{array}\right),$$ (40)

$${\tilde{t}}_{{{{\rm{N}}}}}=\tilde{t}({k}_{y}),$$ (41) with the chemical potentials in left (right)-side superconductors _μ_L (_μ_R), and the normal layer _μ_N, respectively.

$${\hat{t}}_{{{{\rm{L0}}}}}={\hat{t}}_{{{{\rm{1R}}}}}={t}_{{{{\rm{int}}}}}\tilde{t}({k}_{y}),$$ (42) with the transparency _t_int. In this calculation, we fix the transparency as _t_int = 

1.0. First, we calculate the semi-infinite surface Green’s function \({\hat{G}}_{{{{\rm{L}}}}}\) and \({\hat{G}}_{{{{\rm{R}}}}}\) in the left and right-side superconductors, respectively54.

When we add a normal layer, we obtain the surface Green’s functions \({\hat{G}}_{{{{\rm{L0}}}}}({k}_{y},i{\varepsilon }_{n})\) and \({\hat{G}}_{{{{\rm{R1}}}}}({k}_{y},i{\varepsilon

}_{n},\phi )\), $${\hat{G}}_{{{{\rm{L0}}}}}({k}_{y},i{\varepsilon }_{n})={[i{\varepsilon }_{n}-{\tilde{u}}_{{{{\rm{N}}}}}-{\hat{t}}_{{{{\rm{L0}}}}}^{{\dagger}

}{\hat{G}}_{{{{\rm{L}}}}}{\hat{t}}_{{{{\rm{L0}}}}}]}^{-1},$$ (43) $${\hat{G}}_{{{{\rm{R1}}}}}({k}_{y},i{\varepsilon }_{n},\phi )={[i{\varepsilon

}_{n}-{\tilde{u}}_{{{{\rm{N}}}}}-{\hat{t}}_{{{{\rm{1R}}}}}{\hat{G}}_{{{{\rm{R}}}}}{\hat{t}}_{{{{\rm{1R}}}}}^{{\dagger} }]}^{-1},$$ (44) with the local term in the normal layer

\({\tilde{u}}_{{{{\rm{N}}}}}\), the tunnel Hamiltonian \({\hat{t}}_{{{{\rm{L0}}}}}={\hat{t}}_{{{{\rm{1R}}}}}\), and the fermionic Matsubara frequency _i__ε__n_ = _i__π_(2_n_ + 1)_k_B_T_. For

the connection of two superconductors with a normal layer, we calculate the local Green’s functions, $${\hat{G}}_{00}({k}_{y},i{\varepsilon }_{n},\phi

)={[{\hat{G}}_{{{{\rm{L0}}}}}^{-1}-{\tilde{t}}_{{{{\rm{N}}}}}{\hat{G}}_{{{{\rm{R1}}}}}{\tilde{t}}_{{{{\rm{N}}}}}^{{\dagger} }]}^{-1},$$ (45) $${\hat{G}}_{11}({k}_{y},i{\varepsilon }_{n},\phi

)={[{\hat{G}}_{{{{\rm{R1}}}}}^{-1}-{\tilde{t}}_{{{{\rm{N}}}}}^{{\dagger} }{\hat{G}}_{{{{\rm{L0}}}}}{\tilde{t}}_{{{{\rm{N}}}}}]}^{-1},$$ (46) and the nonlocal Green’s functions,

$${\hat{G}}_{01}({k}_{y},i{\varepsilon }_{n},\phi )={\hat{G}}_{{{{\rm{L0}}}}}{\tilde{t}}_{{{{\rm{N}}}}}{\hat{G}}_{11},$$ (47) $${\hat{G}}_{10}({k}_{y},i{\varepsilon }_{n},\phi

)={\hat{G}}_{{{{\rm{R1}}}}}{\tilde{t}}_{{{{\rm{N}}}}}^{{\dagger} }{\hat{G}}_{00}.$$ (48) DATA AVAILABILITY The data that support the findings of this study are available from the

corresponding author upon reasonable request. CODE AVAILABILITY The code that supports the findings of this study is available from the corresponding author upon reasonable request.

REFERENCES * Josephson, B. D. Possible new effects in superconductive tunnelling. _Phys. Lett._ 1, 251–253 (1962). Article  ADS  MATH  Google Scholar  * Likharev, K. K. Superconducting weak

links. _Rev. Mod. Phys._ 51, 101–159 (1979). Article  ADS  Google Scholar  * Bardeen, J. & Johnson, J. L. Josephson current flow in pure superconducting-normal-superconducting junctions.

_Phys. Rev. B_ 5, 72–78 (1972). Article  ADS  Google Scholar  * Ishii, C. Josephson currents through junctions with normal metal barriers. _Prog. Theor. Phys._ 44, 1525–1547 (1970). Article

  ADS  Google Scholar  * Kulik, I. O. Nonlinear high-frequency properties of thin superconducting films. _Sov. Phys. JETP_ 30, 329–337 (1970). ADS  Google Scholar  * Kulik, I. O. &

Omelyanchuk, A. N. Josephson effect in superconductive bridges: microscopic theory. _J. Phys. Colloq._ 39, 546–547 (1978). Article  Google Scholar  * Furusaki, A. & Tsukada, M. Dc

Josephson effect and Andreev reflection. _Solid State Commun._ 78, 299–302 (1991). Article  ADS  Google Scholar  * Buzdin, A. Direct coupling between magnetism and superconducting current in

the Josephson _φ_0 junction. _Phys. Rev. Lett._ 101, 107005 (2008). Article  ADS  Google Scholar  * Tanaka, Y., Yokoyama, T. & Nagaosa, N. Manipulation of the Majorana fermion, Andreev

reflection, and Josephson current on topological insulators. _Phys. Rev. Lett._ 103, 107002 (2009). Article  ADS  Google Scholar  * Yokoyama, T., Eto, M. & Nazarov, Y. V. Anomalous

Josephson effect induced by spin-orbit interaction and Zeeman effect in semiconductor nanowires. _Phys. Rev. B_ 89, 195407 (2014). Article  ADS  Google Scholar  * Golubov, A. A., Kupriyanov,

M. Y. & Il’ichev, E. The current-phase relation in Josephson junctions. _Rev. Mod. Phys._ 76, 411–469 (2004). Article  ADS  Google Scholar  * Tanaka, Y. & Kashiwaya, S. Phase

dependent energy levels of bound states and d.c. Josephson current in unconventional superconductor / ferromagnetic insulator / unconventional superconductor junctions. _J. Phys. Soc. Jpn._

69, 1152–1161 (2000). Article  ADS  Google Scholar  * Asano, Y., Tanaka, Y., Sigrist, M. & Kashiwaya, S. Josephson current in s-wave-superconductor/Sr2RuO4 junctions. _Phys. Rev. B_ 67,

184505 (2003). Article  ADS  Google Scholar  * Grein, R., Eschrig, M., Metalidis, G. & Schön, G. Spin-dependent Cooper pair phase and pure spin supercurrents in strongly polarized

ferromagnets. _Phys. Rev. Lett._ 102, 227005 (2009). Article  ADS  Google Scholar  * Eschrig, M. & Löfwander, T. Triplet supercurrents in clean and disordered half-metallic ferromagnets.

_Nat. Phys._ 4, 138–143 (2008). Article  Google Scholar  * Silaev, M. A., Tokatly, I. V. & Bergeret, F. S. Anomalous current in diffusive ferromagnetic Josephson junctions. _Phys. Rev.

B_ 95, 184508 (2017). Article  ADS  Google Scholar  * Konschelle, F. & Buzdin, A. Magnetic moment manipulation by a Josephson current. _Phys. Rev. Lett._ 102, 017001 (2009). Article  ADS

  Google Scholar  * Alidoust, M., Shen, C. & Žutić, I. Cubic spin-orbit coupling and anomalous Josephson effect in planar junctions. _Phys. Rev. B_ 103, L060503 (2021). Article  ADS 

Google Scholar  * Van Harlingen, D. J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—evidence for \({d}_{{x}^{2}-{y}^{2}}\) symmetry.

_Rev. Mod. Phys._ 67, 515–535 (1995). Article  ADS  Google Scholar  * Goldobin, E., Koelle, D., Kleiner, R. & Buzdin, R. A. Josephson junctions with second harmonic in the current-phase

relation: Properties of _φ_ junctions. _Phys. Rev. B_ 76, 224523 (2007). Article  ADS  Google Scholar  * Goldobin, E., Koelle, D., Kleiner, R. & Mints, R. G. Josephson junction with a

magnetic-field tunable ground state. _Phys. Rev. Lett._ 107, 227001 (2011). Article  ADS  Google Scholar  * Yerin, Y. S. & Omelyanchouk, A. N. Frustration phenomena in Josephson point

contacts between single-band and three-band superconductors. _Low. Temp. Phys._ 40, 943–950 (2014). Article  ADS  Google Scholar  * Sickinger, H. et al. Experimental evidence of a _φ_

Josephson junction. _Phys. Rev. Lett._ 109, 107002 (2012). Article  ADS  Google Scholar  * Guarcello, C., Chirolli, L., Mercaldo, M. T., Giazotto, F. & Cuoco, M. Frustration-driven

Josephson phase dynamics. _Phys. Rev. B_ 105, 134503 (2022). Article  ADS  Google Scholar  * Tanaka, Y. & Kashiwaya, S. Theory of the josephson effect in _d_-wave superconductors. _Phys.

Rev. B_ 53, R11957–R11960 (1996). Article  ADS  Google Scholar  * Tanaka, Y. & Kashiwaya, S. Theory of josephson effects in anisotropic superconductors. _Phys. Rev. B_ 56, 892–912

(1997). Article  ADS  Google Scholar  * Barash, Y. S., Burkhardt, H. & Rainer, D. Low-temperature anomaly in the Josephson critical current of junctions in _d_-wave superconductors.

_Phys. Rev. Lett._ 77, 4070–4073 (1996). Article  ADS  Google Scholar  * Kashiwaya, S. & Tanaka, Y. Tunnelling effects on surface bound states in unconventional superconductors. _Rep.

Prog. Phys._ 63, 1641–1724 (2000). Article  ADS  Google Scholar  * Szombati, D. B. et al. Josephson _ϕ_0-junction in nanowire quantum dots. _Nat. Phys._ 12, 568–572 (2016). Article  Google

Scholar  * Ahmad, H. et al. Coexistence and tuning of spin-singlet and triplet transport in spin-filter Josephson junctions. _Commun. Phys._ 5, 2 (2022). Article  ADS  Google Scholar  *

Gingrich, E. C. et al. Controllable 0-_π_ josephson junctions containing a ferromagnetic spin valve. _Nat. Phys._ 12, 564–567 (2016). Article  Google Scholar  * Di Bernardo, A. et al. Nodal

superconducting exchange coupling. _Nat. Mater._ 18, 1194–1200 (2019). Article  ADS  Google Scholar  * Chen, C.-T., Tsuei, C. C., Ketchen, M. B., Ren, Z.-A. & Zhao, Z. X. Integer and

half-integer flux-quantum transitions in a niobium-iron pnictide loop. _Nat. Phys._ 6, 260–264 (2010). Article  Google Scholar  * Stornaiuolo, D. et al. Signatures of unconventional

superconductivity in the LaAlO3/SrTiO3 two-dimensional system. _Phys. Rev. B_ 95, 140502(R) (2017). Article  ADS  Google Scholar  * Singh, G. et al. Gate-tunable pairing channels in

superconducting non-centrosymmetric oxides nanowires. _NPJ Quantum Mater._ 7, 2 (2022). Article  ADS  Google Scholar  * Kirtley, J. R. Probing the order parameter symmetry in the cuprate

high temperature superconductors by squid microscopy. _Comptes Rendus Phys._ 12, 436–445 (2011). Article  ADS  Google Scholar  * Frigeri, P. A., Agterberg, D. F., Koga, A. & Sigrist, M.

Superconductivity without inversion symmetry: MnSi versus CePt3Si. _Phys. Rev. Lett._ 92, 097001 (2004). Article  ADS  Google Scholar  * Scheurer, M. S. & Schmalian, J. Topological

superconductivity and unconventional pairing in oxide interfaces. _Nat. Commun._ 6, 6005 (2015). Article  ADS  Google Scholar  * Mercaldo, M. T., Solinas, P., Giazotto, F. & Cuoco, M.

Electrically tunable superconductivity through surface orbital polarization. _Phys. Rev. Appl._ 14, 034041 (2020). Article  ADS  Google Scholar  * Fukaya, Y. et al. Inter-orbital topological

superconductivity in spin-orbit coupled superconductors with inversion symmetry breaking. _Phys. Rev. B_ 97, 174522 (2018). Article  ADS  Google Scholar  * Bal, V. V. et al. Gate-tunable

superconducting weak link behavior in top-gated LaAlO3-SrTiO3. _Appl. Phys. Lett._ 106, 212601 (2015). Article  ADS  Google Scholar  * Sigrist, M. & Ueda, K. Phenomenological theory of

unconventional superconductivity. _Rev. Mod. Phys._ 63, 239–311 (1991). Article  ADS  Google Scholar  * Park, S. R., Kim, C. H., Yu, J., Han, J. H. & Kim, C. Orbital-angular-momentum

based origin of Rashba-type surface band splitting. _Phys. Rev. Lett._ 107, 156803 (2011). Article  ADS  Google Scholar  * Park, J.-H., Kim, C. H., Rhim, J.-W. & Han, J. H. Orbital

Rashba effect and its detection by circular dichroism angle-resolved photoemission spectroscopy. _Phys. Rev. B_ 85, 195401 (2012). Article  ADS  Google Scholar  * Khalsa, G., Lee, B. &

MacDonald, A. H. Theory of _t_2_g_ electron-gas Rashba interactions. _Phys. Rev. B_ 88, 041302(R) (2013). Article  ADS  Google Scholar  * Kim, P., Kang, K. T., Go, G. & Han, J. H. Nature

of orbital and spin Rashba coupling in the surface bands of SrTiO3 and KTaO3/. _Phys. Rev. B_ 90, 205423 (2014). Article  ADS  Google Scholar  * Fukaya, Y. et al. Spin-orbital hallmarks of

unconventional superconductors without inversion symmetry. _Phys. Rev. B_ 100, 104524 (2019). Article  ADS  Google Scholar  * Fukaya, Y., Yada, K., Tanaka, Y., Gentile, P. & Cuoco, M.

Orbital tunable 0-_π_ transitions in Josephson junctions with noncentrosymmetric topological superconductors. _Phys. Rev. B_ 102, 144512 (2020). Article  ADS  Google Scholar  * Sato, M.,

Tanaka, Y., Yada, K. & Yokoyama, T. Topology of Andreev bound states with flat dispersion. _Phys. Rev. B_ 83, 224511 (2011). Article  ADS  Google Scholar  * Yada, K., Sato, M., Tanaka,

Y. & Yokoyama, T. Surface density of states and topological edge states in noncentrosymmetric superconductors. _Phys. Rev. B_ 83, 064505 (2011). Article  ADS  Google Scholar  * Brydon,

P. M. R., Schnyder, A. P. & Timm, C. Topologically protected flat zero-energy surface bands in noncentrosymmetric superconductors. _Phys. Rev. B_ 84, 020501(R) (2011). Article  ADS 

Google Scholar  * Mercaldo, M. T., Cuoco, M. & Kotetes, P. Magnetic-field-induced topological reorganization of a _p_-wave superconductor. _Phys. Rev. B_ 94, 140503(R) (2016). Article 

ADS  Google Scholar  * Lee, P. A. & Fisher, D. S. Anderson localization in two dimensions. _Phys. Rev. Lett._ 47, 882–885 (1981). Article  ADS  Google Scholar  * Umerski, A. Closed-form

solutions to surface Green’s functions. _Phys. Rev. B_ 55, 5266–5275 (1997). Article  ADS  Google Scholar  * Kawai, K. et al. Josephson effect in a multiorbital model for Sr2RuO4. _Phys.

Rev. B_ 95, 174518 (2017). Article  ADS  Google Scholar  * Asano, Y. Josephson spin current in triplet superconductor junctions. _Phys. Rev. B_ 74, 220501 (2006). Article  ADS  Google

Scholar  * Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. _Nature_ 427, 423–426 (2004). Article  ADS  Google Scholar  * Reyren, N. et al.

Superconducting interfaces between insulating oxides. _Science_ 317, 1196–1199 (2007). Article  ADS  Google Scholar  * Fernandes, R. M., Haraldsen, J. T., Wölfle, P. & Balatsky, A. V.

Two-band superconductivity in doped SrTiO3 films and interfaces. _Phys. Rev. B_ 87, 014510 (2013). Article  ADS  Google Scholar  * Caviglia, A. D. et al. Electric field control of the

LaAlO3/SrTiO3 interface ground state. _Nature_ 456, 624–627 (2008). Article  ADS  Google Scholar  * Thierschmann, H. et al. Transport regimes of a split gate superconducting quantum point

contact in the two-dimensional LaAlO3/SrTiO3 superfluid. _Nat. Commun._ 9, 2276 (2018). Article  ADS  Google Scholar  * Hurand, S. et al. Field-effect control of superconductivity and Rashba

spin-orbit coupling in top-gated LaAlO3/SrTiO3 devices. _Sci. Rep._ 5, 12751 (2015). Article  ADS  Google Scholar  * Caviglia, A. D. et al. Tunable Rashba spin-orbit interaction at oxide

interfaces. _Phys. Rev. Lett._ 104, 126803 (2010). Article  ADS  Google Scholar  * Ben Shalom, M., Sachs, M., Rakhmilevitch, D., Palevski, A. & Dagan, Y. Tuning spin-orbit coupling and

superconductivity at the LaAlO3/SrTiO3 interface: A magnetotransport study. _Phys. Rev. Lett._ 104, 126802 (2010). Article  ADS  Google Scholar  * Joshua, A., Pecker, S., Ruhman, J., Altman,

E. & Ilani, S. A universal critical density underlying the physics of electrons at the LaAlO3/SrTiO3 interface. _Nat. Commun._ 3, 1129 (2012). Article  ADS  Google Scholar  * Herranz,

G. et al. Engineering two-dimensional superconductivity and Rashba spin-orbit coupling in LaAlO3/SrTiO3 quantum wells by selective orbital occupancy. _Nat. Commun._ 6, 6028 (2015). Article 

ADS  Google Scholar  * Singh, G. et al. Gap suppression at a Lifshitz transition in a multi-condensate superconductor. _Nat. Mater._ 18, 948–954 (2019). Article  ADS  Google Scholar  *

Trevisan, T. V., Schütt, M. & Fernandes, R. M. Unconventional multiband superconductivity in bulk SrTiO3 and LaAlO3-SrTiO3 interfaces. _Phys. Rev. Lett._ 121, 127002 (2018). Article  ADS

  Google Scholar  * Kalaboukhov, A. et al. Homogeneous superconductivity at the LaAlO3-SrTiO3 interface probed by nanoscale transport. _Phys. Rev. B_ 96, 184525 (2017). Article  ADS  Google

Scholar  * Kuerten, L. et al. In-gap states in superconducting LaAlO3-SrTiO3 interfaces observed by tunneling spectroscopy. _Phys. Rev. B_ 96, 014513 (2017). Article  ADS  Google Scholar  *

Brydon, P. M. R. & Manske, D. 0-_π_ transition in magnetic triplet superconductor josephson junctions. _Phys. Rev. Lett._ 103, 147001 (2009). Article  ADS  Google Scholar  * Mercaldo, M.

T., Kotetes, P. & Cuoco, M. Magnetoelectrically tunable Andreev bound state spectra and spin polarization in p-wave Josephson junctions. _Phys. Rev. B_ 100, 104519 (2019). Article  ADS

  Google Scholar  * Kotetes, P., Mercaldo, M. T. & Cuoco, M. Synthetic Weyl points and chiral anomaly in Majorana devices with nonstandard andreev-bound-state spectra. _Phys. Rev. Lett._

123, 126802 (2019). Article  ADS  MathSciNet  Google Scholar  * Sakurai, K. et al. Nodal Andreev spectra in multi-Majorana three-terminal Josephson junctions. _Phys. Rev. B_ 101, 174506

(2020). Article  ADS  Google Scholar  * Gentile, P. et al. Spin-orbital coupling in a triplet superconductor-ferromagnet junction. _Phys. Rev. Lett._ 111, 4 (2013). Article  Google Scholar 

Download references ACKNOWLEDGEMENTS This research has recevied funding by ERA-NET QUANTERA European Union’s Horizon H2020 project “QUANTOX” under Grant Agreement No. 731473. M.C., P.G., and

Y.F. acknowledge support by the project “Two-dimensional Oxides Platform for SPINorbitronics nanotechnology (TOPSPIN)” funded by the MIUR-PRIN Bando 2017 - grant 20177SL7HC. M.C.

acknowledges support by the EU’s Horizon 2020 research and innovation program under Grant Agreement nr. 964398 (SUPERGATE). This work is supported by the JSPS KAKENHI (Grants No. JP18H01176,

No. JP18K03538, No. JP20H00131, and No. JP20H01857) from MEXT of Japan, Researcher Exchange Program between JSPS and RFBR (Grant No. JPJSBP120194816), and the JSPS Core-to-Core program

Oxide Superspin international network (Grants No. JPJSCCA20170002). We acknowledge valuable discussions with C. Guarcello and M.T. Mercaldo. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS *

CNR-SPIN, c/o Universitá di Salerno, I-84084 Fisciano, Salerno, Italy Yuri Fukaya, Paola Gentile & Mario Cuoco * Department of Applied Physics, Nagoya University, Nagoya, 464-8603, Japan

Yuri Fukaya, Yukio Tanaka & Keiji Yada Authors * Yuri Fukaya View author publications You can also search for this author inPubMed Google Scholar * Yukio Tanaka View author publications

You can also search for this author inPubMed Google Scholar * Paola Gentile View author publications You can also search for this author inPubMed Google Scholar * Keiji Yada View author

publications You can also search for this author inPubMed Google Scholar * Mario Cuoco View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS The

project was designed and supervised by M.C. Y.F. carried out the theoretical computation concerning the behavior of the Josephson current, the analysis of the order parameter texture, and

their dependence on the electronic and thermal parameters. All authors contributed extensively to the discussion, the conception and the analysis of the results presented in this paper. The

paper has been written by M.C. and Y.F. with substantial contributions from all authors. CORRESPONDING AUTHOR Correspondence to Mario Cuoco. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION 41535_2022_509_MOESM1_ESM.PDF Supplemental Material: Anomalous Josephson Coupling and High-Harmonics in Non-Centrosymmetric Superconductors with

s-wave Spin-Triplet Pairing RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,

adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a

credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted

use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT

THIS ARTICLE CITE THIS ARTICLE Fukaya, Y., Tanaka, Y., Gentile, P. _et al._ Anomalous Josephson coupling and high-harmonics in non-centrosymmetric superconductors with _S_-wave spin-triplet

pairing. _npj Quantum Mater._ 7, 99 (2022). https://doi.org/10.1038/s41535-022-00509-8 Download citation * Received: 23 March 2022 * Accepted: 13 September 2022 * Published: 28 September

2022 * DOI: https://doi.org/10.1038/s41535-022-00509-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable

link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative