Angle-dependent magnetoresistance and its implications for lifshitz transition in w2as3

ABSTRACT Lifshitz transition represents a sudden reconstruction of Fermi surface structure, giving rise to anomalies in electronic properties of materials. Such a transition does not

necessarily rely on symmetry-breaking and thus is topological. It holds a key to understand the origin of many exotic quantum phenomena, for example, the mechanism of extremely large

magnetoresistance (MR) in topological Dirac/Weyl semimetals. Here, we report studies of the angle-dependent MR (ADMR) and the thermoelectric effect in W2As3 single crystal. The compound

shows a large unsaturated MR (of about 7000% at 4.2 K and 53 T). The most striking finding is that the ADMR significantly deforms from the horizontal dumbbell-like shape above 40 K to the

vertical lotus-like pattern below 30 K. The window of 30–40 K also corresponds substantial changes in Hall effect, thermopower and Nernst coefficient, implying an abrupt change of Fermi

surface topology. Such a temperature-induced Lifshitz transition results in a compensation of electron-hole transport and the large MR as well. We thus suggest that the similar method can be

applicable in detecting a Fermi-surface change of a variety of quantum states when a direct Fermi-surface measurement is not possible. SIMILAR CONTENT BEING VIEWED BY OTHERS EMERGENCE OF

FERMI ARCS DUE TO MAGNETIC SPLITTING IN AN ANTIFERROMAGNET Article 23 March 2022 TEMPERATURE-DEPENDENT FERMI SURFACE PROBED BY SHUBNIKOV–DE HAAS OSCILLATIONS IN TOPOLOGICAL SEMIMETAL

CANDIDATES DYBI AND HOBI Article Open access 20 December 2023 EVIDENCE OF SUPERCONDUCTING FERMI ARCS Article Open access 07 February 2024 INTRODUCTION A Lifshitz transition means an abrupt

change of the Fermi surface topology of metals without symmetry breaking,1 therefore, it is also termed as electronic topological transition. Conventional Lifshitz transition is _quantum_

phase transition at zero temperature, driven by chemical doping, magnetic field, pressure or uniaxial stress, in the vicinity of which the topology of the Fermi surface deforms.2,3,4,5

Indeed, such Lifshitz transition is associated with a variety of emergent quantum phenomena such as van-Hove singulary, non-Fermi-liquid behavior, unconventional superconductivity et al. A

recent famous example is Sr2RuO4, whose \(\gamma\)-Fermi sheet hits the edge of Brillouine zone and forms a van-Hove singularity under uniaxial stress. The critical transition temperature

increases from \(\sim\)1.5 K up to \(\sim\)3.5 K,5 and meanwhile transport, magnetic and thermodynamic properties change correspondingly.6,7 Besides those quantum control parameters,

temperature can be regarded as another driving force to induce a Lifshitz transition, because the chemical potential (\({\mu }_{F}\)) is temperature-dependence and its shift can modify the

Fermi surface structure.8 However, such realistic examples are rare9,10,11 due to the stringent requirements: (i) small Fermi energy (\({\varepsilon }_{F}\) in the order of

\({k_B}T\;\lesssim\; 100\) meV), so that the varying temperature can be influential to \({\mu }_{F}\) with respect to \({\varepsilon }_{F}\); (ii) band structure near the Fermi energy

displaying anomalous dispersion, so that the contoured Fermi surface experiences an abrupt change. Recently, a wide spectrum of topological semimetals have been extensively studied including

Dirac semimetals (DSM),12,13,14 Weyl semimetals (WSM)15,16,17,18,19,20 as well as nodal-line semimetals.21,22,23 These topological semimetals have bearing on a common feature: the extremely

large magnetoresistance (MR),11,24,25,26,27,28,29 here the MR is defined as the percentage of the change of resistance in an applied magnetic field. Unlike previously colossal/giant MR

observed in some magnetic materials, these newly discovered topological semimetals are generally nonmagnetic. Different mechanisms have been proposed to be responsible for the extremely

large MR, including conventional electron-hole compensation,24 topological protection,30 open-orbit effect,31 and quantum limit.32 Therefore, what is the origin of MR in these semimetals is

still under debate. In addition, these compounds usually hold of small \({\varepsilon }_{F}\) and complicated band structure near Fermi level, and hence set up a natural platform to search

for new examples of temperature-induced Lifshitz transition. On the other hand, the Fermi surface in materials plays a key role in unveiling the mechanism of MR, because its topology

translates into charge carriers trajectory, and hence electrical conductivities, in magnetic fields. For some topological semimetals with multi-band Fermi sheets, their Fermi surfaces are

very complex and actually material-dependence, and the extrinsic control parameters can tune the deformation of Fermi surface topology. Therefore, a direct Fermi-surface measurement is

usually very hard and high-intensive. At this point, the measurements of angular dependent magnetoresistance (ADMR), as a simple and effective method to probe the information of Fermi

surface or the possible topological phase transition in these materials, are highly required. In this work, we first report a temperature-induced Lifshitz transition between 30 and 40 K in a

candidate topological semimetal W2As3 by ADMR measurements. In the window of temperature the extremely large MR starts to appear correspondingly. We speculate that a downward shift of

chemical potential as \(T\) decreases has caused the emergence of a new hole pocket below 30 K, which fulfills the electron-hole compensation and leads to the extremely large MR. All of Hall

effect, thermopower and Nernst effect measurements further lend support for this conclusion. We thus demonstrate the important role of electron-hole compensation to the extremely large MR

in such kind of topological semimetal. Apart from this, we also suggest that the simple ADMR measurements can be applicable in detecting a Fermi-surface change in a variety of quantum states

at a low expense, especially when a direct Fermi-surface measurement is not possible. RESULTS AND DISCUSSION Before displaying our experimental results, it is necessary to briefly elucidate

the ADMR as an effective technique to detect the Fermi surface anisotropy. For more details, the readers may refer to the refs. 33,34 In uncorrelated compounds, MR typically originates from

the bending of carrier trajectory. Watching in the momentum space, electrons (or holes) perform orbits about Fermi surface cross-sections perpendicular to \({\bf{B}}\). Considering a simple

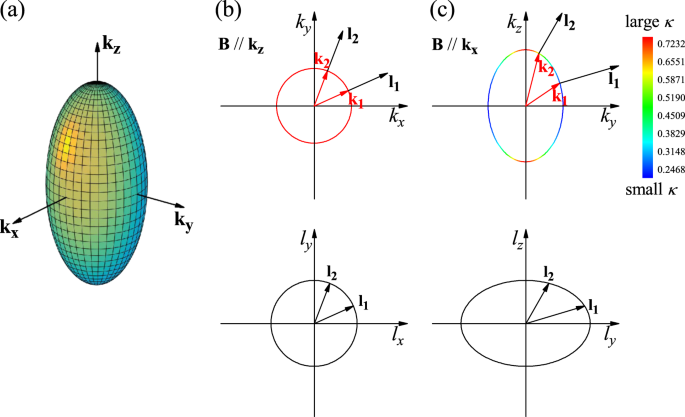
case, an ellipsoidal Fermi surface elongates along \({{\bf{k}}}_{{\bf{z}}}\), as shown in Fig. 1. For \({\bf{B}}\parallel {{\bf{k}}}_{{\bf{z}}}\) (Fig. 1b), the Fermi surface cross-section

perpendicular to \({\bf{B}}\) is a circle. The scattering path length vector, defined as \({{\bf{l}}}_{{\bf{k}}}={{\bf{v}}}_{{\bf{k}}}\tau\) (where \({{\bf{v}}}_{{\bf{k}}}=\frac{1}{\hslash

}{\nabla }_{{\bf{k}}}{\varepsilon }_{{\bf{k}}}\)), sweeps out a circle in the \({\bf{l}}\) space. Whereas for \({\bf{B}}\parallel {{\bf{k}}}_{{\bf{x}}}\) (Fig. 1c), the Fermi surface

cross-section now is an ellipse with variable local curvature \(\kappa\). The swept out \({\bf{l}}\) curve also becomes non-uniform. The anisotropic shape of the Fermi surface causes

different cyclotron masses and \({{\bf{v}}}_{{\bf{k}}}\) (which depends on the local curvature of FS) under various field orientations, which has an effect on the ease of trajectory bending

under magnetic fields and the value of MR as well. The situation becomes more interesting in a semimetal with multiple Fermi surfaces, as the anisotropy now further affects the degree of

carrier compensation and leads to strongly angular dependent MR.34 ADMR, thus, is deemed as a powerful method to reflect the change of Fermi surface in transports. The Fermi surface topology

can be more complicated in realistic materials, e.g., multiple Fermi surface pockets, open Fermi surface, or Fermi surface with anomalous curvatures. Such ADMR measurements, however, are

still useful to unveil the Fermi surface characteristics. A typical example is the conventional semimetal Bismuth.35,36 The compound studied in this work, W2As3, was originally synthesized

over a half century ago.37 It crystalizes in a monoclinic structure C2/\(m\) (No. 12) with the angle spanned by A and C being _β_ = 124.7°. For many decades, the physical properties of W2As3

have remained unclear until recently, Li et al. reported the large MR and the Shubnikov de Hass (SdH) quantum oscillations.38 The topological nature was also suggested by first-principles

calculation. Besides that, the abnormal transport properties in this system, such as angular dependent magnetoresistance (ADMR) and thermoelectric effect, which are associated with the

anisotropy of Fermi surface and the possible topological phase transition, are really of absence. Figure 2a displays the longitudinal resistivity (\(\rho \equiv {\rho }_{xx}\)) of W2As3 as a

function of temperature (\(T\)) down to 2 K with the electrical current \({\bf{I}}\parallel {\bf{b}}\) and the applied magnetic field \({\bf{B}}\parallel {\bf{a}}\) (cf. Fig. 3b). For \(B\)

 = 0, \({\rho }_{xx}(T)\), displays highly metallic behavior, attains a magnitude of 315 μΩ cm at room temperature but falls to 1.04 μΩ cm (=\({\rho }_{0}\)) at 2 K, yielding a large

residual resistivity ratio RRR = 303, comparable with the previous finding.38 The \({\rho }_{xx}(T)\) decreases sublinearly for _T_ > 80 K, and gradually evolves into a power-law for _T_ 

< 40 K. We write down the formula \({\rho }_{xx}\;=\;{\rho }_{0}\;+\;A{T}^{n}\), and display the results of \(\mathrm{log}({\rho }_{xx}-{\rho }_{0})\) vs. \(\mathrm{log}(T)\) in the inset

of Fig. 2a, giving rise to the exponent \(n\) = 3.32(6). The \(n\) value accidently falls in between \(n=\) 2 for \(e-e\) scattering and \(n=\) 5 for electron-phonon (\(e-ph\)) scattering

process according to the Bloch-Gruneisen theory,39 and is very close to \(n=\) 3 and 4 for LaBi and LaSb.26,40 The application of a magnetic field does not change the resistivity too much in

the high temperature region, but enhances it substantially below \({T}_{m}\;\approx\;30-40\) K. The origin of \({T}_{m}\) will be discussed in detail later on. For low fields, \({\rho

}_{xx}(T)\) tends to saturate at low temperatures; as \(B\) increases, the field-induced upturn in \({\rho }_{xx}(T)\) becomes more and more prominent, resulting in the large

magnetoresistance \(\mathrm{MR}\;\equiv\;(\rho (B)-\rho (0))/\rho (0)\). Similar behavior has been observed in many other topological semimetals.18,24,26 The MR as a function of \(B\) for

several selected temperatures is shown in Fig. 2b. The positive MR with a parabolic field-dependence reaches a value of 2300% at 9 T and 2 K. The MR decreases rapidly with increasing

temperature and finally holds less than a few percentages at 200 K, analogous to the most of topological semimetals. To verify the unsaturated MR at the higher magnetic field, we perform the

pulsed-field measurements up to 53 T at 4.2 K, as shown in the inset to Fig. 2b. The magnitude of MR reaches about 70,000% at 53 T without any signature of saturation. Different to the

Dirac semi-metal Cd3As2 with the linear MR,30 here the MR follows a nearly perfect parabolic field-dependence, implying the perfectly compensated electron and hole system predicted by the

two-band theory,24,39 $${\rho }_{xx}(B)=\frac{1}{e}\frac{({n}_{h}{\mu }_{h}+{n}_{e}{\mu }_{e})+({n}_{h}{\mu }_{e}+{n}_{e}{\mu }_{h}){\mu }_{h}{\mu }_{e}{B}^{2}}{{({n}_{h}{\mu

}_{h}+{n}_{e}{\mu }_{e})}^{2}+{({n}_{h}-{n}_{e})}^{2}{\mu }_{h}^{2}{\mu }_{e}^{2}{B}^{2}},$$ (1) where \({n}_{e}\) (\({n}_{h}\)) and \({\mu }_{e}\) (\({\mu }_{h}\)) are electron (hole)

carrier densities and mobilities, respectively. The equality of \({n}_{e}\) and \({n}_{h}\) gives rise to exact \({B}^{2}\) law of \({\rho }_{xx}(B)\), therefore, the compensated semimetals

usually exhibit the large MR, such as in WTe2, TaAs2 and LaSbTe.24,28,41 In addition, the increase of carrier mobilities (see Fig. 4c) in these semimetals is also beneficial to the large MR,

because the MR (\(\propto {\mu }_{h}{\mu }_{e}{B}^{2}\)) is proportional to the mobility at low temperatures. The wiggles on top of the parabolic background stemming from the SdH

oscillations will be discussed further hereafter. Another striking finding in our sample W2As3 is the deformation of ADMR below \({T}_{m}\). The geometry of our measurement is depicted in

Fig. 3b. The field-rotation is about \({\bf{b}}\)-axis and thus is kept to be perpendicular to electric current. One can clearly see the ADMR, and more interestingly, these patterns change

dramatically with temperature. In Fig. 3c–i, we show the ADMR in polar plots at selected temperatures between 2 and 50 K. Above 35 K, the ADMR exhibits strong twofold symmetry at 9 T (Fig.

3c), highly consistent with the configuration of centro-symmetry crystal structure in W2As3. This dumbbell-like pattern suggests anisotropy Fermi surface. The maximum of resistance occurs at

\(\theta =0\) (\({\bf{B}}\parallel {\bf{a}}\)), and the minimum localizes at _θ_ = 90°, while no clear feature can be identified at around \(\theta =\beta\) (i.e., \({\bf{B}}\parallel

{\bf{c}}\)). As \(T\) decreases to 34 K, four extra lobes show up around \(n\pi /3\) (\(n\;=\;\pm1,\;\pm2\)). Further decreasing temperature, the resistivity for _θ_  =  90° grows very

rapidly, and finally this takes over the maximum (Fig. 3e–h). The similar feature retains down to 2 K. Over the full temperature range 2–50 K, the resistivity for \(\theta =0\) keeps a local

maximum although a very shallow dip emerges in the vicinity of \({\bf{B}}\parallel {\bf{a}}\) at very low temperatures. Whereas, what attracts us most is that the pattern of ADMR changes

from a horizontal dumbbell-like to a vertical lotus-like, in the temperature range from 40 to 30 K. This reminds us of the Lifshitz transition of which the topology of Fermi surface

undergoes a substantial reconstruction. Hall effect and thermoelectric effect are very sensitive to the electronic structure of sample. We present the results of Hall resistivity (\({\rho

}_{yx}\)), thermopower (\(S\)), and Nernst coefficient (\(\upsilon\)) in Fig. 4. The Hall resistivity, as shown in Fig. 4a, is essentially negative for all the measured temperatures (2–100 

K) and fields (0–9 T), manifesting that electrons are the majority carrier. For \(T\;>\) 70 K, \({\rho }_{yx}(B)\) is essentially linear with \(B\). It starts to decrease gradually and

bends strongly at high magnetic fields below 50 K. As T \(\le\) 30 K, a positive slope in \({\rho }_{yx}\)(B) above \(\sim\)6 T is observed. The slope extends gradually to low magnetic

fields and becomes more prominent until 15 K, where \({\rho }_{yx}\) becomes slightly positive at 9 T. The reversed slope between 40 and 30 K gives also a clue to the change of electronic

structure. Below 10 K, \({\rho }_{yx}\)(B) increases reversely, recovers the nearly linear behavior and holds the negative slope in the measured magnetic field range. The changed slope and

the non-linear field-dependence in \({\rho }_{yx}\)(B) strongly suggest a multi-band system in W2As3, as reported in other semimetals.25,26,42 For simplicity, we adopt a two-band model, with

one electron- and one hole-bands. In this model, the Hall conductivity \(\left ({\sigma }_{xy}=\frac{{\rho }_{yx}}{{\rho }_{xx}^{2}+{\rho }_{yx}^{2}}\right)\) reads as,39 $${\sigma

}_{xy}(B)=eB \left[\frac{{n}_{h}{{\mu }_{h}}^{2}}{1+{({\mu }_{h}B)}^{2}}-\frac{{n}_{e}{{\mu }_{e}}^{2}}{1+{({\mu }_{e}B)}^{2}}\right].$$ (2) Particular attention was paid to this fitting

(see “Method” section), and the derived results are summarized in Fig. 4c. At 100 K, electron-type carrier density \({n}_{e}\) dominates, while the mobilities of electron and hole are

essentially the same, indicating that at this temperature the system can more or less be regarded as a single-band system, which is in contrast to the majority of hole-type carrier density

in the previous report.38 Lowering temperature, the \({n}_{e}\) only slightly decreases with \(T\) (be noted the \(\mathrm{log}\) scale of \({n}_{e,h}\)) while the \({n}_{h}\) significantly

increases in the temperature range 30–40 K. For \(T\le\) 25 K, \({n}_{e,h}\) tends to saturate and becomes comparable, confirming a nearly compensated electron-hole carrier densities in

W\({}_{2}\)As\({}_{3}\). On the other hand, the mobility shows a large divergency below 40 K, with the value \({\mu }_{e}\) much larger than \({\mu }_{h}\) at low temperature, consistent

with the recovered negative slope in \({\rho }_{xy}\)(B). All these features suggest a change of electronic structure at around 30–40 K. The region 30–40 K from now on will be termed as

\({T}_{m}\). Considering the rapid increase of \({n}_{h}\) near \({T}_{m}\), it is reasonable to assume that a new hole pocket shows up, and thus drastically modifies the electronic

structure. Similar behaviors were observed in WTe\({}_{2}\) and MoTe\({}_{2}\) semimetals.9,11 This also gives an explanation to the change of ADMR near \({T}_{m}\), as the new hole pocket

inevitably will change the anisotropy of Fermi surface. As the extracted carrier mobilities (\({\mu }_{e,h}\)) are in the range of 103–4 cm2/Vs, we thus can calculate the value of \({\omega

}_{c}\tau =\mu B \sim 3\) as \(B\) = 3 T, which is still far away from the high field regime (\({\omega }_{c}\tau \gg 1\)). In addition, the MR in a conventional metal should be saturated in

the high field regime.43 However, in our sample such saturation behavior is not observed and the extremely large MR still follows the parabolic field-dependence even for the field up to 53 

T. This implies that simply entering high field regime is not sufficient in this context, and the carrier compensation effect should be more important. Additional evidences for such a

temperature-induced Lifshitz transition can be provided by thermoelectric measurements. The thermopower is negative from 2 to 300 K, confirming again electrons as the majority carrier. The

zero-field thermopower divided by temperature (\(S/T\)) in Fig. 4d shows a non-monotonic temperature-dependence with a local maximum (in magnitude) at 40 K. Although this might be

reminiscent of the phonon drag effect, the region that it starts to drop agrees surprisingly well with \({T}_{m}\), it, therefore, is more likely that such behavior is of electronic origin.

Applying a magnetic field up to 9 T obviously enhances the magnitude of \(S\) and suppresses the local maximum of thermopower towards the low temperatures (Fig. 3d). Such behavior is in

contrast to the robust thermopower under magnetic fields caused by the phonon drag effect, as reported in FeGa\({}_{3}\).44 We also measured the transverse magneto-thermoelectric transport,

viz. Nernst effect. Here we adopt a classical sign convention by which the Nernst effect caused by vortex motion is positive. It is apparently seen that above 50 K, the Nernst coefficient

divided by temperature (\(\upsilon /T\)) is negligibly small. It is well known that for a single-band, nonsuperconducting and nonmagnetic metal, the Nernst signal is vanishing, due to the

so-called Sondheimer cancellation.45 Such a cancellation is violated below 40 K, and the magnitude of \(\upsilon /T\) increases rapidly. A relevant example of large Nernst effect is the

compensated semimetal Bi46 because of the equal density of electrons and holes in bands. The change in \(\upsilon /T\) observed near \({T}_{m}\) in W\({}_{2}\)As\({}_{3}\), again, is in

agreement with a temperature-induced Lifshitz transition. Turning now to the SdH quantum oscillations. Since systematic SdH studies have been reported recently in ref., 38 we do not plan to

get into too many details. After subtracting a smooth polynomial background from the total resistivity, the remaining part, \(\rho\)−\(\langle \rho \rangle\), is shown in Fig. 5a as a

function of \(1/B\). The clear SdH oscillations were observed and the most of oscillation patterns consist of a main frequency \(F\) = 337 T, in spite of some sub-features observed only for

field above 50 T that is potentially due to the Zeeman effect. More SdH frequencies can be visible if we take Fast Fourier Transform (Data not shown here). Since \({\rho

}_{xx}(B)\)\(\gg\)\({\rho }_{yx}\) in W\({}_{2}\)As\({}_{3}\), the maxima of the SdH oscillations in \({\rho }_{xx}(B)\) is assigned as integer Landau level (LL) indices \(n\) (See e.g.,

ref. 47), as shown in Fig. 5b. A linear extrapolation of \(n\) versus 1/\(B\) to the infinite field limit yields the intercept of −0.10(3). According to the Lifshitz-Kosevich formula, this

intercept corresponds to \(1/2-{\Phi }_{B}/2\pi -\delta\),48 where \({\Phi }_{B}\) is the Berry phase, and \(-1/8\le \delta \le 1/8\) is an additional phase shift stemming from the curvature

of the Fermi surface topology. This means that a trivial (non-trivial) Berry phase gives rise to an intercept close to 0 (0.5). The intercept derived here, \(\sim\)−0.10(3), falls between

\(\pm\)1/8, and thus should point to a non-trivial topological feature. In short, from SdH-oscillation measurements we confirm W2As3 is a topological semimetal. This same conclusion was also

drawn by Li et al.;38 there more Fermi sheets with different Berry phases were resolved. The Fermi surface structure has also been reported in Li’s work,38 and several _close_ pockets, both

electron- and hole-types, are shown by DFT calculations. For simplicity, a _schematic_ band structure of W2As3 can be proposed based on all these results, see Fig. 5c. The compound should

contain at least one topological band that has Dirac-like, linear dispersion. Considering a much higher electron mobility than hole mobility, it is more likely that this non-trivial band is

of electron-type, as seen in Fig. 5c. At high temperature, the chemical potential \({\mu }_{F}\) passes through this Dirac band only. The top of valence band is supposed to sit right below

\({\mu }_{F}\). As temperature decreases, the chemical potential moves downward and when \(T\;=\;{T}_{m}\;\sim\;30-40\) K, \({\mu }_{F}\) hits the top of a valence band, generating a great

amount of holes that lead to the electron-hole compensation and large MR at low temperature. The emergence of the new hole pocket changes the anisotropy of Fermi surface, bearing the

consequence for the modification of ADMR patterns. The thermoelectric properties also change correspondingly. To be more straightforward, a semi-quantitative density of states [DOS,

\(N(\varepsilon )\)] can be drawn in this picture [cf. Fig. 5d]. Note that a three dimensional Dirac dispersion renders \(N(\varepsilon )\propto {\varepsilon }^{2}\) (see the red curve in

Fig. 5d). For \(T\;\to\;0\), \({\mu }_{F}\) resides inside the valence band. A rule of thumb about the movement of chemical potential with raising temperature is that it shifts towards the

side that has _smaller_ DOS, which in our case is to move up. This is because the electron density is $${n}_{e}={\int_{{\mu }_{F}}^{+\infty}}N(\varepsilon )f(\varepsilon )d\varepsilon ,$$

(3) and the hole density is $${n}_{h}={\int_{-\infty}^{{\mu }_{F}}}N(\varepsilon )[1-f(\varepsilon )]d\varepsilon ,$$ (4) where \(f(\varepsilon )\) = \(\frac{1}{1\;+\;\exp

(\varepsilon\;-\;{\mu }_{F})/T}\) is Fermi-Dirac distribution function. The electron (for \(\varepsilon\) above \({\mu }_{F}\)) and hole (for \(\varepsilon\) below \({\mu }_{F}\))

distributions have been depicted by the pink and magenta areas in the right panel of Fig. 5d, respectively. As \(T\) increases, \(f(\varepsilon )\) becomes more smeared-out, and therefore,

\({n}_{h}\) increases faster than \({n}_{e}\); \({\mu }_{F}\) has to move up to compensate. According to the Mott relation,39 the thermopower is \(S=\frac{{\pi }^{2}{k}_{B}^{2}T}{3e{\sigma

}_{xx}}\frac{\partial {\sigma }_{xx}(\varepsilon )}{\partial \varepsilon }{| }_{\varepsilon ={\mu }_{F}}\). Previous theoretic work by Blanter et al. predicted a maximum in thermopower when

\({\mu }_{F}-{\varepsilon }_{c}\)\(\to\)0,49 where \({\varepsilon }_{c}\) is the critical energy as a Lifshitz transition takes place. In our case this corresponds to the top of valence

band. Such a maximum of thermopower (in magnitude) is indeed seen in our experiment as shown in Fig. 4d. The realistic band structure of W\({}_{2}\)As\({}_{3}\), although, is more

complicated,38 but such a temperature-induced Lifshitz transition seems rather likely. Finally, it is worthwhile to mention that, one difficulty that we have to confront when comparing the

experimental results to the theoretical calculations is that we do not know exactly where the chemical potential pins to. DFT calculation loses its power in this context because it varies in

realistic samples, depending on the content of nonstoichiometry and disorder. Angle-resolved photoemission spectroscopy (ARPES) is required to further clarify the problem, as it is the case

in WTe2.9 In conclusion, compared with the previous study in W2As3,38 besides the large unsaturated MR, more importantly, we first find that the ADMR of W2As3 depends strongly on

temperature, and undergoes an obvious deformation from the horizontal dumbbell-like shape above 40 K to the vertical lotus-like pattern below 30 K. Such feature implies a dramatic

reconstruction of Fermi surface. Hall effect measurements indicate an abnormal increase in hole carrier density below 40 K, around which thermopower exhibits a large reversal while Nernst

coefficient increases abnormally. All of these experimental results point to an interesting Lifshitz transition occurring between 30–40 K, which in turn leads to the compensated

electron-hole carrier density, as well as the large MR in W2As3. Our works not only pave an important path to investigate the origin of large MR, but also suggest that the simple ADMR

measurement will be applicable in detecting a Fermi-surface change of a variety of quantum states at a low expense but high convenience, especially when a direct Fermi-surface measurement is

not possible. METHOD Single crystals W2As3 were grown through chemical vapor transport reaction using iodine as transport agent. Polycrystalline samples of W2As3 were first synthesized by

solid state reaction using high purified Tungsten powders and Arsenic powders in a sealed quartz tube at 973 K for three days. The final powders together with a transport agent iodine

concentration of 10 mg/cm3 were mixed thoroughly and then sealed in a quartz tube with a low vacuum-pressure of \(\le\)10−3 Pa. The tube was heated in a horizontal tube furnace with a

temperature gradient of 120 °C between 1120 °C and 1000 °C for 1–2 weeks. The obtained high-quality single crystals are shiny and black with the hexagonal-shape. X-ray diffraction patterns

were performed using a D/Max-rA diffractometer with CuK\({}_{\alpha }\) radiation and a graphite monochromator at the room temperature. The single crystal X-ray diffraction determines the

crystal grown orientation. The energy dispersive X-ray (EDX) spectroscopy was employed to verify the composition of the crystals, yielding a fairly homogenous stoichiometric ratio. No iodine

impurity can be detected in these single crystals. Electrical transport measurements were performed using the standard six-terminal method with electric current flowing in parallel to the

\({\bf{b}}\)-axis. Ohmic contacts were carefully prepared on the crystal in a Hall-bar geometry. The low contact resistance was obtained after annealing the silver paste at 573 K for an

hour. Thermoelectric properties were measured by a steady-state technique and a pair of differential type-E thermocouples was used to measure the temperature gradient. The field dependence

of thermocouple was pre-calibrated carefully. All these measurements were carried out in a commercial Quantum Design PPMS-9 system with a rotator insert. The resistivity measurements under a

pulsed magnetic field up to 53 T were performed in Wuhan National High Magnetic Field Center. In Fig. 4, we performed the fitting of two band model in Hall data by two ways. First, we

started to independently fit the Hall data at 100 K, and yielded the carrier densities and mobilities. For the next temperature 70 K, we employed the values at 100 K as the initial

parameters, and thus gets the reliable fitting for 80 K. The same procedure keeps on until we finished the last temperature 2 K. Second, in order to get a further check, we also

_independently_ started the fitting at 2 K, and gradually moved back to 100 K. The obtained two sets of parameters by this opposite way are in good agreement. Such self-consistent fitting

method makes our fitting results reliable. DATA AVAILABILITY All data generated or analyzed during this study are included in the present paper. REFERENCES * Lifshitz, I. M. Anomalies of

electron characteristics of a metal in the high pressure region. _Sov. Phys. JETP_ 11, 1130–1135 (1960). Google Scholar  * Liu, C. et al. Evidence for a lifshitz transition in electron-doped

iron arsenic superconductors at the onset of superconductivity. _Nat. Phys._ 6, 419–423 (2010). Article  Google Scholar  * Li, C. H. et al. Pressure-induced topological phase transitions

and strongly anisotropic magnetoresistance in bulk black phosphorus. _Phys. Rev. B_ 95, 125417 (2017). Article  ADS  Google Scholar  * Pfau, H. et al. Interplay between kondo suppression and

lifshitz transitions in YbRh2Si2 at high magnetic fields. _Phys. Rev. Lett._ 110, 256403 (2013). Article  ADS  Google Scholar  * Steppke, A. et al. Strong peak in \({T}_{c}\) of Sr2RuO4

under uniaxial pressure. _Science_ 355, 6321 (2017). Article  Google Scholar  * Barber, M. E., Gibbs, A. S., Maeno, Y., Mackenzie, A. P. & Hicks, C. W. Resistivity in the vicinity of a

van Hove Singularity: Sr2RuO4 under uniaxial pressure. _Phys. Rev. Lett._ 120, 076602 (2018). Article  ADS  Google Scholar  * Luo, Y. K. et al. Normal state 17O NMR studies of Sr2RuO4 under

uniaxial stress. _Phys. Rev. X_ 9, 021044 (2019). Google Scholar  * Ashcroft, N. W. & Mermin, N. D. _Solid State Phys_. (Harcourt College Publishers, 1976). * Wu, Y. et al.

Temperature-induced lifshitz transition in WTe2. _Phys. Rev. Lett._ 115, 166602 (2015). Article  ADS  Google Scholar  * Zhang, Y. et al. Electronic evidence of temperature-induced lifshitz

transition and topological nature in ZrTe5. _Nat. Commun._ 8, 15512 (2017). Article  ADS  Google Scholar  * Zhou, Q. et al. Hall effect within the colossal magnetoresistive semimetallic

state of MoTe2. _Phys. Rev. B_ 94, 121101 (2016). Article  ADS  Google Scholar  * Wang, Z. J. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). _Phys. Rev. B_

85, 195320 (2012). Article  ADS  Google Scholar  * Liu, Z. K. et al. Discovery of a three-dimensional topological dirac semimetal, Na3Bi. _Science_ 343, 864–867 (2014). Article  ADS  Google

Scholar  * Jeon, S. et al. Landau quantization and quasiparticle interference in the three-dimensional dirac semimetal Cd3As2. _Nat. Mater._ 13, 851–856 (2014). * Weng, H. M., Fang, C.,

Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. _Phys. Rev. X_ 5, 011029 (2015). Google Scholar  * Lv, B. Q. et al.

Observation of Weyl nodes in TaAs. _Nat. Phys._ 11, 724–727 (2015). Article  Google Scholar  * Lv, B. Q. et al. Experimental discovery of weyl semimetal TaAs. _Phys. Rev. X_ 5, 031013

(2015). Google Scholar  * Xu, S. Y. et al. Discovery of a weyl fermion semimetal and topological fermi arcs. _Science_ 349, 613–617 (2015). Article  ADS  Google Scholar  * Shekhar, C. et al.

Extremely large magnetoresistance and ultrahigh mobility in the topological weyl semimetal candidate NbP. _Nat. Phys._ 11, 645–649 (2015). Article  Google Scholar  * Ghimire, N. J. et al.

Magnetotransport of single crystalline NbAs. _J. Phys.: Condens. Mat._ 27, 152201 (2015). ADS  Google Scholar  * Fang, C., Weng, H. M., Dai, X. & Fang, Z. Topological nodal line

semimetals. _Chin. Phys. B_ 25, 117106 (2016). Article  ADS  Google Scholar  * Bian, G. et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2. _Nat. Commun._ 7, 10556 (2016).

Article  ADS  Google Scholar  * Neupane, M. et al. Observation of topological nodal fermion semimetal phase in ZrSiS. _Phys. Rev. B_ 93, 201104 (2016). Article  ADS  Google Scholar  * Ali,

M. N. et al. Large, non-saturating magnetoresistance in WTe\({}_{2}\). _Nature_ 514, 205–208 (2014). Article  ADS  Google Scholar  * Luo, Y. et al. Hall effect in the extremely large

magnetoresistance semimetal WTe2. _Appl. Phys. Lett._ 107, 182411 (2015). Article  ADS  Google Scholar  * Tafti, F. F., Gibson, Q. D., Kushwaha, S. K., Haldolaarachchige, N. & Cava, R.

J. Resistivity plateau and extreme magnetoresistance in LaSb. _Nat. Phys._ 12, 3581 (2015). Google Scholar  * Li, Y. K. et al. Resistivity plateau and negative magnetoresistance in the

topological semimetal TaSb2. _Phys. Rev. B_ 94, 121115 (2016). Article  ADS  Google Scholar  * Luo, Y. K. et al. Anomalous electronic structure and magnetoresistance in TaAs2. _Sci. Rep._ 6,

27294 (2016). Article  ADS  Google Scholar  * Yuan, Z. J., Lu, H., Liu, Y. J., Wang, J. F. & Jia, S. Large magnetoresistance in compensated semimetals TaAs2 and NbAs2. _Phys. Rev. B_

93, 184405 (2016). Article  ADS  Google Scholar  * Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the dirac semimetal Cd3As2. _Nat. Mat._ 14, 280–284 (2015). Article 

Google Scholar  * Pippard, A. B. _Magnetoresistance in Metals_. (Cambridge University Press, 1989). * Abrikosov, A. A. Quantum magnetoresistance. _Phys. Rev. B_ 58, 2788 (1998). Article  ADS

  Google Scholar  * Ong, N. P. Geometric interpretation of the weak-field hall conductivity in two-dimensional metals with arbitrary fermi surface. _Phys. Rev. B_ 43, 193–201 (1991). Article

  ADS  Google Scholar  * Zhang, S. N., Wu, Q. S., Liu, Y. & Yazyev, O. V. Magnetoresistance from fermi surface topology. _Phys. Rev. B_ 99, 035142 (2019). Article  ADS  Google Scholar  *

Zhu, Z. W., Collaudin, A., Fauque, B., Kang, W. & Behnia, K. Fieldinduced polarization of dirac valleys in bismuth. _Nat. Phys._ 8, 89 (2011). Article  Google Scholar  * Collaudin, A.,

Fauque, B., Fuseya, Y., Kang, W. & Behnia, K. Angle dependence of the orbital magnetoresistance in bismuth. _Phys. Rev. X_ 5, 021022 (2015). Google Scholar  * Jensen, P., Kjekshus, A.

& Skansen, T. Crystal structures of Mo2As3 and W2As3. _Acta Chemica Scandinavica_ 20, 1003–1015 (1966). Article  Google Scholar  * Li, Y. P. et al. Quantum transport in a compensated

semimetal W2As3 with nontrivial Z\({}_{2}\) indices. _Phys. Rev. B_ 98, 115145 (2018). * Ziman, J. M. _Electrons and phonons: the theory of transport phenomena in solids_. (Oxford University

Press, 1960). * Sun, S. S., Wang, Q., Guo, P. J., Liu, K. & Lei, H. C. Large magnetoresistance in LaBi: Origin of field-induced resistivity upturn and plateau in compensated semimetals.

_New J. Phys._ 18, 082002 (2016). Article  ADS  Google Scholar  * Singha, R., Pariari, A., Satpati, B. & Mandal, P. Magnetotransport properties and evidence of topological insulating

state in LaSbTe. _Phys. Rev. B_ 96, 245138 (2017). Article  ADS  Google Scholar  * Zhang, C. L. et al. Electron scattering in tantalum monoarsenide. _Phys. Rev. B_ 95, 085202 (2017). Article

  ADS  Google Scholar  * Du, X., Tsai, S. W., Maslov, D. L. & Hebard, A. F. Metal-insulator-like behavior in semimetallic bismuth and graphite. _Phys. Rev. Lett._ 94, 166601 (2005).

Article  ADS  Google Scholar  * Wagner-Reetz, M. et al. Phonon-drag effect in FeGa3. _Phys. Rev. B_ 90, 195206 (2014). Article  ADS  Google Scholar  * Sondheimer, E. H. The theory of the

galvanomagnetic and thermomagnetic effects in metals. _Proc. R. Soc. A_ 193, 484–512 (1948). * Behnia, K., Méasson, M. & Kopelevich, Y. Nernst effect in semimetals: The effective mass

and the figure of merit. _Phys. Rev. Lett._ 98, 076603 (2007). Article  ADS  Google Scholar  * Xiang, F. X., Wang, X. L., Veldhorst, M., Dou, S. X. & Fuhrer, M. S. Observation of

topological transition of fermi surface from a spindle torus to a torus in bulk rashba spin-split BiTeCl. _Phys. Rev. B_ 92, 035123 (2015). Article  ADS  Google Scholar  * Murakawa, H. et

al. Detection of Berrys phase in a bulk Rashba semiconductor. _Science_ 342, 1490–1493 (2013). Article  ADS  Google Scholar  * Blanter, Y. M., Kaganov, M. I., Pantsulaya, A. V. &

Varlamov, A. A. The theory of electronic topological transitions. _Phys. Rep._ 245, 159–257 (1994). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This research was

supported in part by the NSF of China (under Grants No. 11874136, U1932155, U1732274). Yu-Ke Li was supported by an open program from Wuhan National High Magnetic Field Center (2016KF03).

Jie Cheng was supported by the General Program of Natural Science Foundation of Jiangsu Province of China (No. BK20171440). Y. Luo acknowledges the 1000 Youth Talents Plan of China. AUTHOR

INFORMATION Author notes * These authors contributed equally: Jialu Wang, Haiyang Yang AUTHORS AND AFFILIATIONS * Department of Physics and Hangzhou Key Laboratory of Quantum Matters,

Hangzhou Normal University, Hangzhou, 311121, China Jialu Wang, Haiyang Yang, Wei You, Chao Cao, Jianhui Dai & Yuke Li * School of Science, Westlake Institute for Advanced Study,

Westlake University, Hangzhou, 310024, China Jialu Wang * Wuhan National High Magnetic Field Center and School of Physics, Huazhong University of Science and Technology, Wuhan, 430074, China

Linchao Ding, Yongkang Luo & Zengwei Zhu * High Magnetic Field Laboratory, Chinese Academy of Sciences, Hefei, 230031, China Chuanying Xi & Mingliang Tian * College of Science,

Center of Advanced Functional Ceramics, Nanjing University of Posts and Telecommunications, Nanjing, Jiangsu, 210023, China Jie Cheng * School of Physics and Key Laboratory of MEMS of the

Ministry of Education, Southeast University, Nanjing, 211189, China Zhixiang Shi Authors * Jialu Wang View author publications You can also search for this author inPubMed Google Scholar *

Haiyang Yang View author publications You can also search for this author inPubMed Google Scholar * Linchao Ding View author publications You can also search for this author inPubMed Google

Scholar * Wei You View author publications You can also search for this author inPubMed Google Scholar * Chuanying Xi View author publications You can also search for this author inPubMed 

Google Scholar * Jie Cheng View author publications You can also search for this author inPubMed Google Scholar * Zhixiang Shi View author publications You can also search for this author

inPubMed Google Scholar * Chao Cao View author publications You can also search for this author inPubMed Google Scholar * Yongkang Luo View author publications You can also search for this

author inPubMed Google Scholar * Zengwei Zhu View author publications You can also search for this author inPubMed Google Scholar * Jianhui Dai View author publications You can also search

for this author inPubMed Google Scholar * Mingliang Tian View author publications You can also search for this author inPubMed Google Scholar * Yuke Li View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS Y. Li designed the research. J. Wang synthesized the samples. J. Wang and H. Yang performed the electronic and thermal transport

measurements. L. Ding performed the resistivity measurements under high magnetic fields in Wuhan. W. You performed the XRD measurements and analyzed the structure parameters. C. Xi and J.

Cheng assisted the measurements. Z. Shi, Y. Luo, Z. Zhu, C. Cao, J. Dai, Y. Li, and M. Tian discussed the data, interpreted the results. Y. Luo, J. Dai, and Y. Li wrote the paper.

CORRESPONDING AUTHORS Correspondence to Yongkang Luo, Jianhui Dai or Yuke Li. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION

PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is

licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, J., Yang, H., Ding, L. _et al._ Angle-dependent

magnetoresistance and its implications for Lifshitz transition in W2As3. _npj Quantum Mater._ 4, 58 (2019). https://doi.org/10.1038/s41535-019-0197-5 Download citation * Received: 23 January

2019 * Accepted: 29 October 2019 * Published: 29 November 2019 * DOI: https://doi.org/10.1038/s41535-019-0197-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative