Guessing probability in quantum key distribution

ABSTRACT On the basis of the existing trace distance result, we present a simple and efficient method to tighten the upper bound of the guessing probability. The guessing probability of the

final key K can be upper bounded by the guessing probability of another key \({\bf{k}}^{\prime}\), if \({\bf{k}}^{\prime}\) can be mapped from the final key K. Compared with the known

methods, our result is more tightened by thousands of orders of magnitude. For example, given a 10−9-secure key from the sifted key, the upper bound of the guessing probability obtained

using our method is 2 × 10−3277. This value is smaller than the existing result 10−9 by more than 3000 orders of magnitude. Our result shows that from the perspective of guessing

probability, the performance of the existing trace distance security is actually much better than what was assumed in the past. SIMILAR CONTENT BEING VIEWED BY OTHERS EXPERIMENTAL QUANTUM

KEY DISTRIBUTION CERTIFIED BY BELL'S THEOREM Article 27 July 2022 SECURITY OF QUANTUM KEY DISTRIBUTION FROM GENERALISED ENTROPY ACCUMULATION Article Open access 29 August 2023

EXPERIMENTAL DEMONSTRATIONS OF UNCONDITIONAL SECURITY IN A PURELY CLASSICAL REGIME Article Open access 18 February 2021 INTRODUCTION The first quantum key distribution (QKD) protocol has

been proposed by Bennett and Brassard in 1984; the protocol was based on the fundamentals of quantum mechanics1. Since then, the security of QKD has always been the central issue in the

quantum cryptographic field2. Trace distance is a very important security criterion3,4. It provides the universal composable security5,6, which can guarantee the security of key regardless

of its application such as one-time pad (OTP). This is why many studies choose trace distance for the security criterion3,4,7,8. In a classical practical cryptosystem, the impact of guessing

probability on security is very important9,10. Specifically, the key generated by the QKD protocol is not based on the presumed hardness of mathematical problems; thus, the eavesdropper Eve

can only guess the final key via the measurement result of her probe. The guessing probability intuitively describes the probability that Eve can correctly guess the final key, which can

reflect the number of guesses that Eve requires to obtain the final key. There are few studies on the guessing probability of QKD. Because there are more rigorous security criterions, such

as the trace distance5,6, which gives the composable security. This makes the theoretical foundation for security of QKD crucially important. However, in the real application of QKD

projects, customers often ask the question of guessing probability. The existing prior art results cannot give them a satisfactory upper bound11. Consequently, some people questioned the

security of QKD by relying on the prior art results of guessing probability12. For example, according to the existing result11, the guessing probability of the _ε_-secure key is

approximately 10−9 if _ε_ is approximately 10−9. From the perspective of guessing probability, the security of the value 10−9 is equivalent to that of a 30 perfect bits. The existing

classical computer systems can easily crack such key. In practice, it is not unusual to request a much smaller guessing probability such as 10−100 or 10−1000. Therefore, it is beneficial to

find a more tightened upper bound of guessing probability. As an important criterion in cryptography, guessing probability alone cannot guarantee the security of the final key. However, the

large value of the loose upper bound of the guessing probability does not indicate the insecurity of the final key12 because the value is not achievable by Eve, and one can find a more

tightened value for the upper bound of the guessing probability. Here, by applying the trace distance criterion2, we find such tightened bound. We show that the guessing probability is

actually smaller than the existing bound values by many orders of magnitude if one takes the privacy amplification by Toeplitz matrix. This shows that the trace distance criterion2 can

actually produce a much better result than what was assumed previously in the viewpoint of guessing probability. RESULTS We consider the security definitions of a practical QKD protocol with

finite size under the framework of composable security3,4,13,14. Suppose that Alice and Bob get two _N_-bit sifted key strings, S and \({\bf{s}}^{\prime}\). By performing an error

correction and private amplification scheme, Alice gets an _n_1-bit key K, and Bob gets an estimate key \(\hat{{\bf{k}}}\) of K from S and \({\bf{s}}^{\prime}\). The protocol is

_ε_cor-correct if \(P[{\bf{k}}\,\ne\, \hat{{\bf{k}}}]\le {\varepsilon }_{{\rm{cor}}}\). In general, the key K of Alice can be correlated with an eavesdropper system, and the density matrix

of Alice and Eve is _ρ_AE. The protocol outputs an _ε_-secure key7, if $$\frac{1}{2}\parallel {\rho }_{{\rm{AE}}}-{\rho }_{{\rm{U}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}\le \varepsilon

,$$ (1) where ∥ ⋅ ∥1 denotes the trace norm, _ρ_U is the fully mixed state of Alice’s system. The protocol is _ε_tol-secure if _ε_cor and _ε_ satisfy _ε_cor + _ε_ ≤ _ε_tol, which means that

it is _ε_tol-indistinguishable from a perfect protocol (which is correct and secret). Without any loss of generality, we consider the case of _ε_cor = _ε_ in this article. We define the

security level: DEFINITION 1 If key K is _ε_-secure, the _security level_ of key K is _ε_ For symbol clarity, we will use notation _ε_K for the security level of key K. With this definition,

we can say that the key K is _ε_K-secure or that its security level is _ε_K We define the guessing probability: DEFINITION 2 Let the final key generated by the QKD protocol be K; the

_guessing probability_ of K is defined as the success probability of the attacker Eve guessing the final key via her measurement result and is denoted as _p_(K). LEMMA 1 _The guessing

probability of_ _ε_K-_secure key_ K _with length_ _n_1 _is not larger than_ \(\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}}\) This is a conclusion from ref. 11. The proof has been

already given in ref. 11; for the convenience of readers, we write the proof again in the “Methods” section According to Lemma 1, the guessing probability of key K can be divided into two

parts; one part \({2}^{-{n}_{1}}\) is related to the length of the key, the other part _ε_K(_n_1) is related to the security level. Under the framework of universally composable security,

when calculating the final key length, we often make the security level to be between 10−9 and 10−24, which is much bigger than \({2}^{-{n}_{1}}\) because _n_1 is often 103, 104, or larger.

Therefore, \({2}^{-{n}_{1}}\) can be ignored and \(p({\bf{k}})\le \bar{p}({\bf{k}}) \sim {\mathcal{O}}(\varepsilon ({\bf{k}}))\). However, the guessing probability of a secure key with a

length of tens of bits can also reach this magnitude. Therefore, when the secure requirements are very high, it is clearly not enough for a key with a length of thousands of bits or even

longer if the upper bound of guessing probability only stops at this magnitude. Therefore, we cannot simply use this formula alone to obtain the upper bound of the guessing probability.

Fortunately, we have a much better way for tightening the bound. The approach will be presented below. LEMMA 2 _If key_ K _can be mapped to string_ \({\bf{k}}^{\prime}\) _by a map_ _M_ _that

is known to Eve, then the guessing probability of_ K _cannot be larger than the guessing probability of string_ \({\bf{k}}^{\prime}\), _i.e._, $$p({\bf{k}})\le p({\bf{k}}^{\prime} ).$$ (2)

_Here_ \(p({\bf{k}}),p({\bf{k}}^{\prime} )\) _are the guessing probabilities of_ K _and_ \({\bf{k}}^{\prime}\)_, respectively_ _Proof_. This lemma is clear because when Eve can correctly

guess K, Eve can obtain \({\bf{k}}^{\prime}\) by knowing the map _M_. Otherwise, Eve can still correctly guess the \({\bf{k}}^{\prime}\) with a probability not less than 0, i.e.,

\(p({\bf{k}}^{\prime} )=p({\bf{k}})+\delta ,\delta \ge 0\). THEOREM 1 _If the_ _ε_K-_secure key_ K _with a length_ _n_1 _can be mapped to the_ \({\varepsilon }_{{\bf{k}}^{\prime} }\)-_secure

key_ \({\bf{k}}^{\prime}\) _with length_ _n_2_, the guessing probability of_ K _cannot be larger than_ \({\bf{k}}^{\prime}\)_, i.e._, $$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime}

)=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} }.$$ (3) _Proof._ This theorem actually requires two conditions: * (i) the final key K can be mapped to the string

\({\bf{k}}^{\prime}\), * (ii) the string \({\bf{k}}^{\prime}\) can be regarded as a \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key. Using the above-mentioned conditions, the proof is

very simple. Given the condition (i), we can apply Lemma 2 to obtain $$p({\bf{k}})\le p({\bf{k}}^{\prime} ).$$ (4) Given the condition (ii), we can apply Lemma 1 to obtain

$$p({\bf{k}}^{\prime} )\le \bar{p}({\bf{k}}^{\prime} )=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} },$$ (5) where \(\bar{p}({\bf{k}}^{\prime} )\) is the upper bound of

\(p({\bf{k}}^{\prime} )\). According to Eqs. (4) and (5), we can obtain $$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime} )=\frac{1}{{2}^{{n}_{2}}}+{\varepsilon }_{{\bf{k}}^{\prime} }.$$ (6) This

ends our proof of Theorem 1 As discussed above, if the length of the final key K and the string \({\bf{k}}^{\prime}\) are very large, then \({2}^{-{n}_{1}}\) and \({2}^{-{n}_{2}}\) can be

ignored. Meanwhile, if _n_2 < _n_1 and \({\varepsilon }_{{\bf{k}}^{\prime} }\,<\,{\varepsilon }_{{\bf{k}}}\), then \({2}^{-{n}_{2}}+{\varepsilon }_{{\bf{k}}^{\prime} } \sim

{\varepsilon }_{{\bf{k}}^{\prime} }\le {\varepsilon }_{{\bf{k}}} \sim {2}^{-{n}_{1}}+{\varepsilon }_{{\bf{k}}}\). Thus, Theorem 1 can provide a tighter upper bound of guessing probability.

Using Theorem 1, it is now possible for us to obtain the upper bound of the guessing probability of the _ε_K-secure key K more tightly. Instead of directly applying Lemma 1, we choose to

first map _k_ to an _n_2-bit string \({\bf{k}}^{\prime} =M({\bf{k}})\). If the string \({\bf{k}}^{\prime}\) itself can be regarded as an \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure final

key, we can apply Theorem 1 by calculating \(\bar{p}({\bf{k}}^{\prime} )\). In addition, we can obtain a much smaller upper bound of the guessing probability of K if \({\varepsilon

}_{{\bf{k}}^{\prime} }\) is very small and _n_2 is not too small. Now, the remaining problems are to determine the map _M_, to make sure that \({\bf{k}}^{\prime} =M({\bf{k}})\) is another

key that is \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure, and to calculate \({\varepsilon }_{{\bf{k}}^{\prime} }\). We start our method with the hashing function in the key distillation.

OUR HASHING FUNCTION We use the key distillation with the random matrix. Denote _R__n__N_ as the _n_ × _N_ random matrix with each element being randomly chosen to be either 0 or 1. In

addition, we represent the _N_-bit sifted string S by a column vector, which contains _N_ elements. To obtain the _n_-bit final key, we use the calculation _R__n__N_S. It can be easily

confirmed that our random matrix belongs to the class of two-universal hashing function family2. Suppose we have distilled out the _n_1-bit key K from the _N_-bit sifted key S through

hashing by our random matrix \({R}_{{n}_{1}N}\). We can map the _n_1-bit key K into the _n_2-bit string \({\bf{k}}^{\prime} =M({\bf{k}})\) by deleting the last _n_1 − _n_2 bits from the key

string K. Clearly, this string \({\bf{k}}^{\prime}\) mapped from K can be also regarded as another final key distilled from the sift key S by the _n_2 × _N_ random hashing matrix

\({R}_{{n}_{2}N}\), which is a submatrix of \({R}_{{n}_{1}N}\). In summary, we have $${\bf{k}}^{\prime} =M({\bf{k}})={R}_{{n}_{2}N}{\bf{s}}.$$ (7) This means that \({\bf{k}}^{\prime}\) is a

string mapped from key K. Moreover, \({\bf{k}}^{\prime}\) can be regarded as another final key of length _n_2 distilled from the sifted key S. Because the two conditions in Theorem 1 are

satisfied, according to Theorem 1, we can obtain a tightened upper bound of _p_(K) with Eq. (3) if we know the security level of key \({\bf{k}}^{\prime}\), i.e., the value of \({\varepsilon

}_{{\bf{k}}^{\prime} }\). Because our random matrix is a class of two-universal hashing function, the value \({\varepsilon }_{{\bf{k}}^{\prime} }\) depends on _n__2_4. The details are shown

in the “Methods” section and explain the calculation of \({\varepsilon }_{{\bf{k}}^{\prime} }\) for _n_2. Hence, in the QKD protocol that uses a random hashing matrix presented here, to

obtain the upper bound of the guessing probability of the _n_1-bit final key K, we can summarize the procedure above by the following scheme: SCHEME (1) Given the _n_1-bit final key K, we

delete its last _n_1 − _n_2 bits and obtain a string \({\bf{k}}^{\prime}\). (2) We regard \({\bf{k}}^{\prime}\) as another possible final key that is \({\varepsilon }_{{\bf{k}}^{\prime}

}\)-secure. Compute the \({\varepsilon }_{{\bf{k}}^{\prime} }\) value of \({\bf{k}}^{\prime}\) with the input parameters _N_ and _n_2. (3) Calculate \(\bar{p}({\bf{k}})\) by Theorem 1

through Eq. (3). Because on our scheme the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) is dependent on _n_2, as shown in the “Methods” section, we can now replace \({\varepsilon

}_{{\bf{k}}^{\prime} }\) by a functional form, \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\). To obtain the tightened upper bound value of the guessing probability in scheme 1, we need to

choose an appropriate _n_2 value. In our calculation, we set the condition $${2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2}),$$ (8) for the appropriate _n_2. For any _n_ > 

_n_2, we have \({\varepsilon }_{{\bf{k}}}(n)\,>\,{\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})={2}^{-{n}_{2}}\); however, for any _n_ < _n_2, we have \({2}^{-n}\,>\,{2}^{-{n}_{2}}\).

In conclusion, if _n_ ≠ _n_2, \({2}^{-n}+{\varepsilon }_{{\bf{k}}}(n)\,>\,{2}^{-{n}_{2}}\). Therefore, in this study, we set \({2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime}

}({n}_{2})\), and obtain a tightened guessing probability \({2}^{-{n}_{2}+1}\). Once we determine the value _n_2 and the corresponding \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\), we

calculate \(\bar{p}({\bf{k}}^{\prime} )\) by Eq. (3). Clearly, this is the upper bound of the guessing probability of the final key K of length _n_1 provided that $${n}_{1}\,>\,{n}_{2}.$$

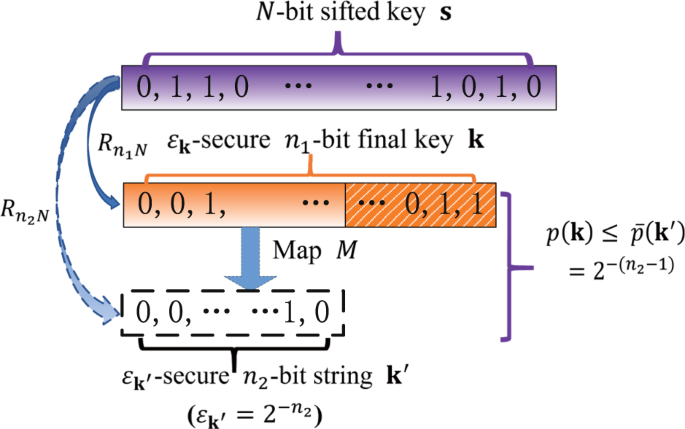
(9) Thus, we can actually use a more efficient scheme to obtain the upper bound of the guessing probability of key K, as the following Theorem 2: As shown in Fig. 1, the arrow between S and

K indicates that the _ε_K-secure _n_1-bit final key K can be distilled from the _N_-bit sifted key S using a random matrix \({R}_{{n}_{1}N}\), i.e. \({\bf{k}}={R}_{{n}_{1}N}{\bf{s}}\). The

arrow between K and \({\bf{k}}^{\prime}\) indicates that there exists a map _M_ that can map the key K into \({\bf{k}}^{\prime}\), i.e., \({\bf{k}}^{\prime} =M({\bf{k}})\). The arrow between

the sifted key S and \({\bf{k}}^{\prime}\) indicates that if a random hashing matrix \({R}_{{n}_{2}N}\) is used to distill the final key, we have \({\bf{k}}^{\prime}

={R}_{{n}_{2}N}{\bf{s}}\). Then if _n_2 satisfies the condition in Theorem 2, a tightened guessing probability of K can be obtained. There are two important points need to be noticed. First,

when applying our theorem to obtain the nontrivial upper bound of the guessing probability for the final key K, we do not really need to transform K to another string \({\bf{k}}^{\prime}\),

and we only need the existence of a map that can map K to \({\bf{k}}^{\prime}\) mathematically. That is to say, we use the final key K, but its guessing probability is calculated from the

shorter key \({\bf{k}}^{\prime}\). As shown above, the existence has been proven. Second, in this study, we use the random matrix _R__n__N_ as a family of two-universal hash functions to

distill the key to illustrate our conclusion more intuitively. Of course, we can also use the modified Toeplitz matrix8 instead of the random matrix _R__n__N_. Thus, the final key K can be

also mapped to the string \({\bf{k}}^{\prime}\), and the string \({\bf{k}}^{\prime}\) can also be regarded as the \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key. This means that the

proposed theorem in this study still holds. THEOREM 2 _In the QKD protocol, if the_ _n_1-_bit final key_ K _is distilled from the sifted key_ S _using a random matrix_ \({R}_{{n}_{1}N}\)_,

the guessing probability of_ _k_ _can be upper bounded by_ $$p({\bf{k}})\le \bar{p}({\bf{k}}^{\prime} )={2}^{-({n}_{2}-1)},$$ (10) _where_ \({\bf{k}}^{\prime}

=M({\bf{k}})={R}_{{n}_{2}N}{\bf{s}}\) _and_ _n_2 _satisfies_ \({2}^{-{n}_{2}}={\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2}),{n}_{2}\,<\,{n}_{1}.\) DISCUSSION Table 1 describes the upper

bounds of the guessing probability calculated by different _N_tol, where _N_tol is the length of the total string that includes the sifted keys for key generation and the string used to do

parameter estimation. In Table 1, _N_tol = 104, 105, and 106. Table 1 shows that when _N_tol = 106, _n_ = 4.90 × 105 and the guessing probabilities obtained using the methods of ref. 12 and

ref. 11 are approximately 10−6 and 10−9, respectively. However, using our method, the guessing probability can be reduced to 2 × 10−3277, which is more tightened by thousands of orders of

magnitude than prior art methods. With an increase in the length of _N_tol, the length of the final key also increases; however, the guessing probabilities in ref. 12 and ref. 11 almost

remain unchanged. Compared with ref. 12 and ref. 11, the guessing probability obtained by our method is considerably reduced, which is more realistic and tighter. It should be noted that we

calculate the case without the known-plaintext attack (KPA) in Table 1. Now, we consider the case of KPA in QKD using our method. Suppose that Eve knows the _t_ bits of the final _n_2-bit

key \({\bf{k}}^{\prime}\); then, the guessing probability of the \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure key \({\bf{k}}^{\prime}\) is \({p}_{{\rm{KPA}}}({\bf{k}}^{\prime} )\le

{2}^{-({n}_{2}-t-1)}\). Now, the upper bound of the guessing probability of key \({\bf{k}}^{\prime}\) is equal to that of an ideal (_n_2 − _t_ − 1)-bit key. Table 2 compares the length of

the _ε_-secure key _n_ and the length of \(\varepsilon ^{\prime}\)-secure key \(n^{\prime}\) when the total length of the sifted key is 104, 105, and 106. This table shows that if only using

Lemma 1 to obtain a smaller guessing probability, _ε_ needs to be reduced. Accordingly, the length of the final key and the key rate will be considerably reduced. For example, from Table 2,

when _N_tol = 106, if the customer wants to reduce the guessing probability from 10−9 to 2 × 10−3277, the length of the key will become \(n^{\prime} =1.1\times 1{0}^{4}\), and the key rate

will become \(r^{\prime} =0.01\). This result is much lower than the original key length _n_ = 4.9 × 105 and the key rate _r_ = 0.49. Using our result, there is actually no bit cost for a

much smaller bound value of guessing probability. For example, when _N_tol = 106, we can upper bound the guessing probability by 2 × 10−3277 by setting _ε_ = 10−9. Thus, without reducing the

value of _ε_, we can obtain a tightened upper bound of guessing probability \({p}_{{\rm{g}}}^{{\rm{Thm.2}}}\) of K, as can be seen from Table 1. Our result shows that in terms of guessing

probability, the performance of the existing trace distance security is much better than what has been assumed in the past. Incidentally, in ref. 11, a looser upper bound, 10−6 for Eve’s

guessing probability, was presented12. We emphasize that this looser upper bound does not in any sense challenge the validity of the existing security proof of QKD11. Although the large

value of _lower bound_ of Eve’s guessing probability can show insecurity, the large value of _upper bound_ cannot show insecurity. If one does not make any effort, one can also obtain a

large-value upper bound of 100% for Eve’s guessing probability. Such value is correct for the upper bound but not meaningful. If any new upper bound is larger than that in the prior art

result, it means that the “new upper bound” is trivial and meaningless rather than the prior art result is invalid. Thus, the looser upper bound presented by ref. 12 only shows that Eve’s

guessing probability of the key is smaller than 10−6. It does not conflict with more tightened results presented elsewhere. In this study, our goal is to obtain a tightened guessing

probability. On the basis of the existing secure criterion (Trace distance) and the general property of guessing probability, we propose a simple and efficient method to tighten the upper

bound of the guessing probability. We find that the guessing probability _p_(K) of K can be upper bounded by \({2}^{-({n}_{2}-1)}\), where _n_2 satisfies \({2}^{-{n}_{2}}={\varepsilon

}_{{\bf{k}}^{\prime} }({n}_{2})\) and _n_2 < _n_1. Specifically, a simple random matrix _R__n__N_ can be used to distill the final key. Compared with the prior art results, of which the

upper bound of the guessing probability of the _ε_-secure key is approximately _ε_, our method provides a more tightened upper bound. Therefore, the loose upper bound for the guessing

probability obtained in ref. 12 cannot be regarded as evidence to question the validity of existing the security proof of QKD. METHODS PROOF OF LEMMA 1 LEMMA 1 _The guessing probability of

the_ _ε_K-_secure key_ K _with length_ _n_1 _is not larger than_ \(\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}}\). This is a conclusion obtained from ref. 11. The proof has been already

presented in ref. 11. Here, for the convenience of the reader, we write the proof again. _Proof_. Let the _n_-bit string X be the _ε_X-secure key in \({\mathcal{X}}\). The density matrix of

Alice and Eve is _ρ_XE and satisfies $${\rho }_{{\rm{XE}}}=\sum _{{\bf{x}}\in {\mathcal{X}}}\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|\otimes {\rho }_{E}^{{\bf{x}}},$$ (11)

$$\frac{1}{2}\parallel {\rho }_{{\rm{XE}}}-{\rho }_{{{\rm{U}}}_{{\bf{x}}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}\le {\varepsilon }_{{\bf{x}}},$$ where \({\rho }_{{{\rm{U}}}_{{\bf{x}}}}\)

is the fully mixed state in \({\mathcal{X}}\). Then we have $$\frac{1}{2}\parallel {\rho }_{{\rm{XE}}}-{\rho }_{{{\rm{U}}}_{{\bf{x}}}}\otimes {\rho }_{{\rm{E}}}{\parallel }_{1}$$ $$\ge

\frac{1}{2}{\left\Vert {\sum \limits_{{\bf{x}}\in {\mathcal{X}}}}q({\bf{x}})\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|-\sum _{{\bf{x}}\in

{\mathcal{X}}}\frac{1}{{2}^{n}}\left|{\bf{x}}\right\rangle \left\langle {\bf{x}}\right|\right\Vert }_{1}$$ (12) $$=\frac{1}{2}{\sum \limits_{{\bf{x}}\in {\mathcal{X}}}}\left\vert

q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert .$$ Eve’s guessing probability of string X is _q_(X), and the maximum guessing probability is \({p}_{{\rm{g}}}={\max }_{{\bf{x}}\in

{\mathcal{X}}}\{q({\bf{x}})\}\). Without any loss of generality, it is possible to assume that the maximum guessing probability is \(q({\bf{x}}^{\prime} )\). Note that \({\sum }_{{\bf{x}}\in

{\mathcal{X}}}q({\bf{x}})=1\), then the following holds $$\frac{1}{2}{\sum }_{{\bf{x}}\in {\mathcal{X}}}\left\vert q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert$$ (13) $$=\frac{1}{2}\left\vert

q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert +\frac{1}{2}{\sum \limits_{{\bf{x}}\in {\mathcal{X}},{\bf{x}}\ne {\bf{x}}^{\prime}}}\left\vert q({\bf{x}})-\frac{1}{{2}^{n}}\right\vert$$

$$\ge \frac{1}{2}\left\vert q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert +\frac{1}{2}\left\vert {\sum \limits_{{\bf{x}}\in {\mathcal{X}},{\bf{x}}\ne

{\bf{x}}^{\prime}}}[q({\bf{x}})-\frac{1}{{2}^{n}}]\right\vert$$ $$=\left\vert q({\bf{x}}^{\prime} )-\frac{1}{{2}^{n}}\right\vert .$$ From Eqs. (11) to (13), we have \({p}_{{\rm{g}}}\le

{2}^{-{n}_{1}}+{\varepsilon }_{{\bf{x}}}\); thus, for the _n_1-bit _ε_K-secure key K, the guessing probability satisfies $$p({\bf{k}})\le

\bar{p}({\bf{k}})=\frac{1}{{2}^{{n}_{1}}}+{\varepsilon }_{{\bf{k}}},$$ (14) where \(\bar{p}({\bf{k}})\) is the upper bound of _p_(K). This ends our proof of Lemma 1. CALCULATION OF

\({\varepsilon }_{{\bf{k}}}^{\prime}\) We consider the security definitions of a practical QKD protocol with a finite size under the framework of composable security4,13,14. Suppose that

Alice and Bob get two _N_-bit sifted key strings. By performing an error correction and private amplification scheme, Alice get an _n_-bit final key K and Bob get an estimate

\(\hat{{\bf{k}}}\) of K. The protocol is _ε_cor-correct if \(P[{\bf{k}}\,\ne\, \hat{{\bf{k}}}]\le {\varepsilon }_{{\rm{cor}}}\). In general, the key K of Alice can be correlated with an

eavesdropper system, and the density matrix of Alice and Eve is _ρ_AE. The protocol outputs an _ε_K-secure key13, if $$\frac{1}{2}\parallel {\rho }_{{\rm{AE}}}-{\rho }_{{\rm{U}}}\otimes

{\rho }_{{\rm{E}}}{\parallel }_{1}\le {\varepsilon }_{{\bf{k}}},$$ (15) where ∥ ⋅ ∥1 denotes the trace norm, _ρ_U is the fully mixed state of Alice's system. The protocol is

_ε_tol-secure if _ε_cor and _ε_K satisfies _ε_cor + _ε_K ≤ _ε_tol, which means that it is _ε_tol-indistinguishable from an ideal protocol. Without any loss of generality, we consider the

case of _ε_cor = _ε_K. From Lemma 1, we can calculate \(\bar{p}({\bf{k}})\) given the _n_-bit _ε_K-secure key K. In this situation, \(\bar{p}({\bf{k}})={2}^{-n}+{\varepsilon }_{{\bf{k}}}\).

However, in our method, we only know _N_ and _n_2, which are the length of the sifted key and \({\bf{k}}^{\prime}\). (The string \({\bf{k}}^{\prime}\) itself can be also regarded as another

final key distilled from the sifted key.) To get a tightened upper bound of the guessing probability of K, we need to obtain the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\). According

to ref. 4, with _N_ and _n_2, the final key is \({\varepsilon }_{{\bf{k}}^{\prime} }\)-secure if \({\varepsilon }_{{\bf{k}}^{\prime} }\) satisfies the following equation: $${n}_{2}\le

N[1-h({Q}_{{\rm{tol}}}+\mu )]-fNh({Q}_{{\rm{tol}}})-\mathrm{log}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }^{3}},$$ (16) where \(\mu

=\sqrt{\frac{N+{N}_{z}}{N{N}_{z}}\frac{{N}_{z}+1}{{N}_{z}}\mathrm{ln}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }}}\), _N__z_ is the length of string used for parameter estimation, _f_ = 

1.1, _h_ denotes the binary Shannon entropy function, \(h(x)=-x\,{\log}\,x-(1-x){\log}\,(1-x)\) and _Q_tol represents the channel error tolerance. To obtain nontrivial results, we use

equality in Eq. (16) to calculate the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\), given the input _n_2. Since \({\varepsilon }_{{\bf{k}}^{\prime} }\) is dependent on _n_2, we use

notation \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\) for \({\varepsilon }_{{\bf{k}}^{\prime} }\). Here, \({\varepsilon }_{{\bf{k}}^{\prime} }({n}_{2})\), if _n_2 is given and we

numerically find the value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) by Eq. (16). In our calculation, we choose a specific _n_2-value that satisfies $${2}^{-{n}_{2}}={\varepsilon

}_{{\bf{k}}^{\prime} }({n}_{2}).$$ (17) In combination with Eq. (16), we obtain the following equation for the tightened \({\varepsilon }_{{\bf{k}}^{\prime} }\) value:

$$-{\log}\,{\varepsilon }_{{\bf{k}}^{\prime} }=N[1-h({Q}_{{\rm{tol}}}+\mu )]-fNh({Q}_{{\rm{tol}}})-{\log}\,\frac{2}{{\varepsilon }_{{\bf{k}}^{\prime} }^{3}},$$ (18) and we can calculate the

value of \({\varepsilon }_{{\bf{k}}^{\prime} }\) and then calculate the guessing probability by Eq. (8) in our main body text. DATA AVAILABILITY The data that support the findings of this

study are available from the corresponding authors upon reasonable request. REFERENCES * Bennett, C. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In

_Proc. IEEE International Conference on Computers, Systems, and Signal Processing_, Bangalore, India, 175−179 (IEEE Press, New York, 1984). * Renner, R. Security of quantum key distribution.

_Int. J. Quantum Inf._ 6, 1 (2008). Article  Google Scholar  * Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. _Nat. Commun._ 5, 3732

(2014). Article  ADS  Google Scholar  * Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. _Nat. Commun._ 3, 634 (2012). Article 

ADS  Google Scholar  * Ben-Or, M., Horodecki, M., Leung, D. W., Mayers, D. & Oppenheim, J. In _Theory of Cryptography Conference_, 386−406 (Springer, 2005). * Renner, R. & König, R.

In _Theory of Cryptography Conference_, 407−425 (Springer, 2005). * König, R., Renner, R., Bariska, A. & Maurer, U. Small accessible quantum information does not imply security. _Phys.

Rev. Lett._ 98, 140502 (2007). Article  ADS  Google Scholar  * Hayashi, M. & Tsurumaru, T. Concise and tight security analysis of the Bennett-Brassard 1984 protocol with finite key

lengths. _N. J. Phys._ 14, 093014 (2012). Article  Google Scholar  * Alimomeni, M. & Safavi-Naini, R. In _International Conference on Information Theoretic Security_, 1−13 (Springer,

2012). * Issa, I. & Wagner, A. B. Measuring secrecy by the probability of a successful guess. _IEEE Trans. Inf. Theory_ 63, 3783 (2017). Article  MathSciNet  Google Scholar  * Portmann,

C. & Renner, R. Cryptographic security of quantum key distribution. Preprint at: https://arxiv.org/abs/1409.3525 (2014). * Yuen, H. P. Security of quantum key distribution. _IEEE Access_

4, 724 (2016). Article  Google Scholar  * Canetti, R. In _Proceedings 2001 IEEE International Conference on Cluster Computing_, 136−145 (IEEE, 2001). * Müller-Quade, J. & Renner, R.

Composability in quantum cryptography. _N. J. Phys_ 11, 085006 (2009). Article  MathSciNet  Google Scholar  Download references ACKNOWLEDGEMENTS We acknowledge the financial support in part

by the Ministry of Science and Technology of China through The National Key Research and Development Program of China grant no. 2017YFA0303901; National Natural Science Foundation of China

grant nos. 11474182, 11774198, 11974204 and U1738142. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * State Key Laboratory of Low Dimensional Quantum Physics, Department of Physics, Tsinghua

University, 100084, Beijing, China Xiang-Bin Wang, Jing-Tao Wang, Ji-Qian Qin, Cong Jiang & Zong-Wen Yu * Jinan Institute of Quantum Technology, SAICT, 250101, Jinan, China Xiang-Bin

Wang * Shenzhen Institute for Quantum Science and Engineering, and Physics Department, Southern University of Science and Technology, 518055, Shenzhen, China Xiang-Bin Wang * Data

Communication Science and Technology Research Institute, 100191, Beijing, China Zong-Wen Yu Authors * Xiang-Bin Wang View author publications You can also search for this author inPubMed 

Google Scholar * Jing-Tao Wang View author publications You can also search for this author inPubMed Google Scholar * Ji-Qian Qin View author publications You can also search for this author

inPubMed Google Scholar * Cong Jiang View author publications You can also search for this author inPubMed Google Scholar * Zong-Wen Yu View author publications You can also search for this

author inPubMed Google Scholar CONTRIBUTIONS X.-B.W. developed the theory, J.-T.W. and J.-Q.Q. contributed equally to the calculation work, C.J. and Z.-W.Y. contributed to simulation work.

All authors contributed to the manuscript. CORRESPONDING AUTHORS Correspondence to Xiang-Bin Wang, Jing-Tao Wang or Zong-Wen Yu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare

no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS

AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in

any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, XB., Wang,

JT., Qin, JQ. _et al._ Guessing probability in quantum key distribution. _npj Quantum Inf_ 6, 45 (2020). https://doi.org/10.1038/s41534-020-0267-3 Download citation * Received: 26 September

2019 * Accepted: 25 March 2020 * Published: 22 May 2020 * DOI: https://doi.org/10.1038/s41534-020-0267-3 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative