A new carbon phase with direct bandgap and high carrier mobility as electron transport material for perovskite solar cells

ABSTRACT Rapid development of perovskite solar cells is challenged by the fact that current semiconductors hardly act as efficient electron transport materials that can feature both high

electron mobility and a well-matched energy level to that of the perovskite. Here we show that T-carbon, a newly emerging carbon allotrope, could be an ideal candidate to meet this

challenge. By using first-principles calculations and deformation potential theory, it is found that T-carbon is a semiconductor with a direct bandgap of 2.273 eV, and the energy level in

the conduction band is lower than that of perovskite by 0.5 eV, showing a larger force of electron injection. Moreover, the calculated electron mobility can reach up to 2.36 × 103 cm2 s–1 

V–1, superior to conventional electron transport materials such as TiO2, ZnO and SnO2, which will facilitate more efficient electron separation and more rapid diffusion away from their locus

of generation within the perovskite absorbers. Furthermore, the bandgap of T-carbon is highly sensitive to strain, thus providing a convenient method to tune the carrier transport

capability. Overall, T-carbon satisfies the requirements for a potential efficient electron transport material and could therefore be capable of accelerating the development of perovskite

solar cells. SIMILAR CONTENT BEING VIEWED BY OTHERS OVERCOMING C60-INDUCED INTERFACIAL RECOMBINATION IN INVERTED PEROVSKITE SOLAR CELLS BY ELECTRON-TRANSPORTING CARBORANE Article Open access

02 December 2022 METAL CHALCOGENIDE ELECTRON EXTRACTION LAYERS FOR _NIP_-TYPE TIN-BASED PEROVSKITE SOLAR CELLS Article Open access 01 November 2024 NON-FULLERENE ELECTRON-TRANSPORTING

MATERIALS FOR HIGH-PERFORMANCE AND STABLE PEROVSKITE SOLAR CELLS Article 04 March 2025 INTRODUCTION In recent years, organic and inorganic hybrid perovskite solar cells (PSCs), a highly

efficient newcomer to the solar cell family, has emerged with great commercial potential to become a leader of next-generation solar energy photovoltaic technology.1,2,3 The power conversion

efficiency (PCE) of PSCs has reached a certified value of 22.7% from 3.8% in a short span of nine years.4,5 PSCs mostly adopt the configuration of transparent electrode/electron transport

material (ETM)/perovskite/hole transport material (HTM)/metal electrode. To increase the PCE, it is essential to precisely manipulate the carriers along the entire pathway from the

perovskite absorber to both electrodes. The ETM is one of the most important components affecting the photovoltaic performance of PSCs by controlling the carrier concentration. A favorable

alignment between the ETM and perovskite allows for the efficient extraction of photogenerated carriers without inducing excessive interface recombination. At present, TiO2 is the most

common and efficient material used as the ETM in PSCs to collect and transport electrons from the perovskite absorber layer.6,7 Nevertheless, although the electron injection rates from the

perovskite absorber to TiO2 ETM are very fast, the electron recombination rates are also very high due to the low electron mobility. Furthermore, the production of conductive crystalline

TiO2 requires relatively high sintering temperatures (400–500 °C). These disadvantages limit its application widely.8 Therefore, the design of a new and efficient ETM is crucial and

imperative for the development of PSCs. An excellent ETM should possess two fundamental properties, where on the one hand, the material should possess high electron mobility to fulfill the

requirement for fast electron transport while avoiding interfacial electron recombination, on the other hand, its energy level is supposed to be well-matched to that of the perovskite to

facilitate electron injection and hole blocking simultaneously.9 Even now, many new ETMs have been reported, including inorganic materials ZnO,10 SnO2,11 WO_x_,12 organic materials C60,13

PC61BM, PC71BM,14,15 and so on. However, the limited improvement on the carrier mobility has not achieved the expectation desired for photovoltaic performance. Here we propose a new

potential ETM candidate, T-carbon, which was initially theoretically predicted to be structurally stable and have excellent electronic properties for wide potential applications by Su et

al.16 in 2011. Recently, Zhang et al.17 successfully turned the prophecy into reality by means of pseudo-topotactic conversion, where T-carbon can be produced from carbon nanotubes under

picosecond laser irradiation in methanol. Moreover, the optical absorption measurements and rough calculation indicate that bulk T-carbon is a semiconductor with a direct bandgap of about

3–5 eV. Up to now, the carrier transport behavior of T-carbon has not been reported in theory and experiment. Thus, in this work, by combining first-principles calculations and deformation

potential (DP) theory,18 the electronic structures and intrinsic mobility of bulk T-carbon are systematically investigated. The theoretical evidence shown in this study demonstrates that

T-carbon is a semiconductor with a desirable moderate direct bandgap of around 3 eV, and the band structure can be modified by the strain effect. Its conduction band energy level matches

well with that of the perovskite, giving it a better advantage in extracting the electron injection from the generation location to the ETM layer. In addition, T-carbon possesses better

carrier transport properties compared with traditional semiconductor materials, especially with respect to its electron transport performance, where its electron mobility can reach up to

2.36 × 103 cm2 s–1 V–1. The excellent properties discovered for T-carbon renders it to be an effective and appropriate candidate as the ETM for high-performance PSCs. RESULTS ELECTRONIC

PROPERTIES In this work, the geometric structure of T-carbon is optimized with the Perdew–Burke–Ernzerhof (PBE) method combined with vdW interactions. The detailed discussion on the lattice

constants and geometry are shown in Note S2 in Supplementary Information (SI). Our results illustrate that the calculated lattice constants are in good agreement with experimental results,

indicating that the method adopted is reliable. The structural stability of T-carbon is also investigated by considering the effect of thermal fluctuation. The root-mean-square deviation

(RMSD) and root-mean-square fluctuation (RMSF) are calculated by molecular dynamics and the results indicate that T-carbon can show good stability in the temperature range of 100–340 K,

which accords with the temperature of perovskites used in PSCs (further discussions are given in Note S2 and Figure S1). Based on the optimized configuration, the band structures of T-carbon

are predicted with PBE, PBEsol,19 and HSE06 functionals20 as well as with different vdW interaction methods including optB86b-vdW,21 optB88-vdW,22 vdW-DF2,23 DFT-D2.24 The detailed results

of the band structures from the above methods are discussed in Note S3. As shown in Fig. S2 and Table S2, it is found that all methods exhibit a direct bandgap character, with PBE and PBEsol

results giving similar bandgaps. Compared with PBE and PBEsol, HSE06 show larger bandgaps. Previous reports have pointed out that PBE and PBEsol functionals tend to underestimate the

bandgap of semiconductors, while the hybrid HSE06 functional can give more accurate results, which are comparable with experimental data.25,26 Moreover, the optB86b-vdW functional can give

further improvement in the description of the binding energy.27 Hence, HSE06 combined with the optB86b-vdW functional is the best selection for the description of electronic properties,

where T-carbon possesses a direct bandgap of 2.273 eV. Furthermore, the band structures near the valence band maximum (VBM) or the conduction band minimum (CBM) exhibit remarkable in-plane

dispersion behavior in the Г to M or Г to R direction in the Brillouin zone, which suggests that bulk T-carbon may have relatively high carrier mobilities. The computed band structure based

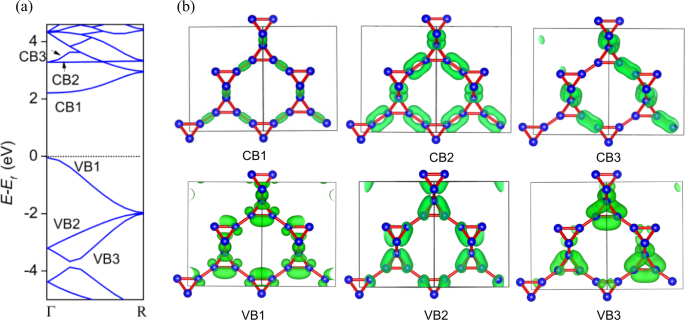
on the HSE06-optB86b-vdW functional is shown in Fig. 1a, from which the orbital charge density on different conduction and valence bands are analyzed (Fig. 1b). In the conduction bands

CB1–CB3, the charge densities are mainly located in the inter-tetrahedron bonds of the structure, while in the valence bands VB1–VB3, the charge densities are mainly distributed in the

tetrahedrons of the structure. Once the atoms in T-carbon experience electronic excitation, appreciable electrons will leap from the valence bands to the conduction bands, gathering holes

within the valence bands. In the excitation process, the electrons transfer from the original intra-tetrahedron bonds to inter-tetrahedron bonds, making the latter have much higher electron

densities with shorter bond characteristics. Therefore, the inter-tetrahedron bonds are relatively stronger than intra-tetrahedron bonds with a better ability to accumulate electrons. The

differences in bond lengths play a crucial role in achieving structural stability by balancing the strain from adjacent tetrahedrons. The corresponding electrostatic potential contour plots

of VB3–CB3 (Fig. S5–S10) show that the electrons are densely localized around the intra-tetrahedron bonds and display a strong covalent bonding feature. However, there is almost no electron

localization in the inter-tetrahedron bonds, which reflect their ionic nature. The interlaced bonding features manifest that each tetrahedron connects with each other through ionic bonds.

This special structural character of T-carbon will make the geometry more stable and is favorable for promoting electron transfer from intra-tetrahedron bonds to inter-tetrahedron bonds. The

three-dimensional contour plots of the VBM and CBM show different distributions and positions of peaks (Fig. 2a). The peaks where electrons accumulate uniformly and locally around the

surface in the CBM reflect antibonding states in the structure, while the conjoint peaks in the VBM means that there exist strong bonding states. Both kinds of peak distributions correspond

to the charge densities located in the CBM and VBM as shown in Fig. 1b. The different distributions in the contour plots shown in both the CBM and VBM reveal a distinct anisotropic behavior

near the Г point for both electrons and holes. A further DOS calculation (Figs. S11–S14) reveals that T-carbon possesses a distinct semiconductor character with strong orbital density in the

conduction bands and relatively weak density in the valence bands. Closer analyses of the electronic orbitals illustrated by the projected density of states (PDOS; Fig. 2b) show that the

conduction bands are dominated by C 2_s_ and 2_p_ orbitals, whereas the valence bands are mainly formed by C 2_p_ orbitals with a rather weak contribution from C 2_s_ orbitals. Besides, the

high hybridization and overlap between _s_ and _p_ orbitals from 3 eV to the top of the conduction band show a strong interactive movement of the excited electrons in the conduction bands,

where electrons will transfer from the lower to higher energy state via the interactive transmission between the different orbitals. This transmission can lead to anisotropic charge

distribution in the energy states where the charge densities are not homogeneously distributed on the intra-tetrahedron and inter-tetrahedron bonds, as shown in Fig. 1b. Similar orbital

hybridization can also be seen in the valence bands. Nevertheless, there is no hybridization at both the top of the valence bands and bottom of the conduction bands, where are singly

composed of 2_p_ and 2_s_ orbitals, respectively. In the band structure, the bandgap is formed between bonding (σ) and antibonding (σ*) orbitals located in the VBM and CBM, respectively. The

direct bandgap at the Г point means that the σ and σ* orbitals are derived from the contributions of 2_p_ and 2_s_ orbitals, respectively. Additionally, the band edges are relatively

dispersed in the vicinity of the Г point, indicative of good carrier transport mobilities.28 In efficient PSCs, the CBM of the ETM should be lower compared with that of the perovskite to

achieve fast electron injection. Previous work has shown that suitable energy level offset can promote the efficient injection of electrons from the perovskite to ETM.29,30,31,32 The energy

level arrangements of T-carbon, popular ETMs (TiO2, SnO2, and ZnO) and frequently used perovskites are provided in Fig. 3a. In the diagram, the CBM energy level of T-carbon is –4.4 eV, close

to that of both SnO2 and ZnO which have been testified to yield quicker charge injection rates as compared to TiO2.9,33,34,35 The similar energy level offset as with SnO2 and ZnO indicates

that T-carbon may also have faster electron injection rate than TiO2, and will thus facilitate more efficient electron acceptance and more rapid diffusion away from their locus of

generation, thereby effectively retarding geminate recombination. As an advantage, the ETM, similar to HTM, is supposed to be colorless, because the ultraviolet–visible (UV–Vis) light

absorption of the ETM would affect the light-harvesting efficiency of the perovskites.36 The optical absorption of T-carbon given by the HSE06-optB86b-vdW functional is shown in Fig. 3b. It

is found that T-carbon shows strong absorption in the ultraviolet range of 180–280 nm. In addition, a cluster model containing 200 atoms (Fig. 3c) based on the TD-B3LYP/6-31G level using

Gaussian 16 code is also calculated,37 for which the maximum absorption is at 249 nm (Fig. 3d), where the excitation energy is 4.94 eV. The dominant transition is from the highest occupied

molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). The HOMO is mainly localized on the center of T-carbon, while the LUMO is located close to the edge. Both the two

calculations manifest that there is no absorption in the visible region. For the classic TiO2 ETM, it has strong absorption at short wavelengths in the range of 300–400 nm.38,39 The optical

absorption of common perovskites are in the range of 300–800 nm.40,41 The overlapping absorption in the UV–Vis region between TiO2 and perovskite will promote competition for the extraction

of photogenerated electrons. Compared with TiO2, the optical calculation of T-carbon favorably highlights its preferential role as the ETM as it will not affect the absorption of perovskite

materials in the visible spectrum. CARRIER MOBILITY For potential ETMs, aside from having a matched energy level, a reasonable high carrier mobility is another indispensable factor. Previous

reports have verified that the high electron mobility of ETMs will facilitate fast extraction and transport photogenerated electrons from perovskites to ETMs, contributing towards improved

_J_SC and high efficiency with negligible _J_–_V_ hysteresis.8,30,31,33,42 For example, PSCs based on SnO2 or ZnO with suitable energy levels and high electron mobility have demonstrated

excellent photovoltaic properties.9,32,33 As shown in Table S3, the calculated carrier mobilities of black phosphorus, MoS2, graphene, etc. based on DP theory are in the same order of

magnitude as their experimental data, which indicates that the method we adopt here to calculate the carrier mobilities of T-carbon is reliable. As shown in Eq. (1), the effective mass has

an important effect on the carrier mobility. The calculated effective masses _m_* are listed in Table 1. Due to the intrinsic cubic structure, _m__x_ = _m__y_ = _m__z_, T-carbon shows an

isotropic transport character. The calculated electron and hole effective masses are 0.22_m_0 and 0.66_m_0, respectively, which are even comparable to those of perovskite MAPbI3/MASnI3

(0.2–1.3_m_0).43 Besides, the hole effective mass is three times larger than that of electrons, which means that the electron transport ability of T-carbon is better than its hole transport

ability. Besides the effective mass, the carrier mobility is also strongly influenced by the 3D elastic constant _C_3D and DP constant _E_1. To compute _C_3D and _E_1, the lattice of the

cell has been dilated and compressed by 1% along the transport direction. The total energies and positions of the VBM and CBM are calculated with respect to the degree of dilation and

compression. All atomic positions are fully relaxed at each dilation and compression step. The electronic energies are obtained at the HSE06-optB86b-vdW level. Figure 4a shows the variation

of total energy with applied uniaxial strain along the lattice direction and _C_3D can be obtained by fitting the energy vs strain curve. Figure 4b depicts the shifts of both band edges VBM

and CBM as a function of uniaxial strain, where _E_1 can be calculated from the slope of the fitted lines. Based on the obtained _m_*, _C_3D, and _E_1, the calculated electron mobility is

found to be 2.36 × 103 cm2 s–1 V–1, which is about 10 times higher than that of holes (2.7 × 102 cm2 s–1 V–1). As the strain range is widened from ±1% to ±2%, ±3%, ±4% and ±5%, respectively,

the variation of carrier mobility mainly depends on changes in _C_3D and _E_1 (Fig. S16 and Table S4). At each strain window setting, the ratio of electron to hole mobility retains the same

value of about 10. Carrier mobility first decreases for the strain range of ±2% before increasing as the strain range is widened from ±3% to ±5%, yet still remaining low with respect to the

initial strain range of ±1%. In view of the changes in carrier mobility subject to tensile strain, we find that the high electron mobility of T-carbon mainly originates from the low

electron effective mass _m_e*. It is worth to mention that the predicted carrier mobilities of T-carbon are comparable and even higher than those of many current popular 2D materials,

traditional semiconductor materials, and perovskites. For example, the electron mobility of T-carbon is distinctly higher than that of various popular 2D materials and semiconductor

materials, such as black phosphorus (103 cm2 s–1 V–1),44 TlO2 (3.3 × 103 cm2 s–1 V–1),45 Si (1.5 × 103 cm2 s–1 V–1),46 and TiO2 (5.24 × 10−2 cm2 s–1 V–1).47 For hole transport performance,

T-carbon reveals significant advantage compared with MoS2 (200 cm2 s–1 V–1),48 perovskite MAPbI3 (1–5 cm2 s–1 V–1),49,50 and TiO2 (0.16 cm2 s–1 V–1).47 In sum, compared with currently

available materials, T-carbon is prospected to have strong transmitting capacity, giving that its high electron mobility can lead to further improved short-circuit current density (_J_SC)

and efficiency.51 Considering the highly effective performance of T-carbon, it is anticipated to be a viable replacement for traditional TiO2 as the ETM. In addition, the strain effect on

the electronic properties of T-carbon (Fig. 5 and Fig. S17) is examined. For both tensile and compressive strain, T-carbon preserves its direct bandgap character. The bandgap increases

linearly from –5% to –2% and from –1 to 0% strain, beyond which it then increases in a soft growth way up to 5% strain where it has a slightly lower slope than that during the compressed

phases. Along with the variation of strain from –1 to 1%, the bandgap fluctuates in the range of –57 to 24 meV relative to that of the equilibrium structure. Interestingly, 1% compressive

strain has a larger effect on the bandgap variation than 1% tensile strain, which means that the compressive treatment has a greater effect on the electronic property of T-carbon than the

tensile stretch. But when the applied strain is higher than 2%, the tensile stretch has larger effect than the compressive treatment as the bandgap can increase by up to 305 meV with respect

to the pristine bandgap. The bandgap evolution under applied strain, as shown in Fig. 5f and Fig. S17i, reflects that T-carbon will show an increasing bandgap with tensile strain and a

declining bandgap with compressive strain. This may provide a new perspective for the development of new functionalities for T-carbon, which can show a tunable band structure according to

the different performance evolving from tensile and compressive strain. DISCUSSION In conclusion, we report a new carbon allotrope as the ETM in PSCs. The electronic properties and carrier

mobility of T-carbon are investigated by first-principles methods and DP theory. The results indicate that T-carbon is a natural semiconductor with a direct bandgap of 2.273 eV. The

conduction band energy level matches well with that of perovskites, which is in favor of electron injection from the point of generation into the ETM layer. Besides, its optical absorption

in the ultraviolet range will not compete against the light harvesting capacity of perovskites in the UV–Vis region. It is more important that T-carbon possesses a high electron mobility of

2.36 × 103 cm2 s–1 V–1, which is superior to that of familiar ETMs such as TiO2, ZnO, SnO2, and even MAPbI3 perovskite. These features portend that T-carbon will be an excellent ETM

candidate for high-performance PSCs. The different band structures that evolve from tensile and compressive strain suggest that imposed strain can be an effective approach to modulate its

transport properties. Based on its special structure and high potential applications, it will be intriguing to embark on experimental investigations to realize these predictions for a

variety of practical applications. METHODS DENSITY FUNCTIONAL THEORY CALCULATIONS For T-carbon, geometry optimization and electronic properties calculations are carried out using density

functional theory (DFT) methods within the generalized gradient approximation and PBE exchange correlation functional, as performed in the Vienna ab initio simulation package (VASP).52 The

ion–electron interactions are described by the projected augmented wave method,53 and the energy cut-off for the plane wave basis is set to 500 eV. Periodic boundary conditions are applied

to all systems. For geometry optimization, a 6 × 6 × 6 Monkhorst Pack grid is adopted, and all the structures are allowed to relax during this process with a conjugate gradient algorithm

until the energy on the atoms is less than 1.0 × 10−5 eV. The maximum force allowed on each atom is 0.01 eV Å−1. Since the van der Waals (vdW) interactions have a great impact on the

geometry and electronic properties,54,55 different vdW correction methods such as the optB86b exchange functional (optB86b-vdW),21,22 optB88 exchange functional (optB88-vdW),22 vdW-DF2

exchange functional23 as well as the DFT-D2 approach proposed by Grimme24 are considered here to accommodate the vdW interactions. For electronic structure calculations, a fine 8 × 8 × 8

grid mesh is used. Since the PBE functional has been known to underestimate the bandgap of semiconductors, PBEsol19 and hybrid HSE06 functional20 methods are also used here to obtain an

accurate bandgap based on the structures obtained from the full optimization with the consideration of vdW interactions. CARRIER MOBILITY CALCULATION For inorganic semiconductors, the

coherent wavelength of thermally activated electrons or holes at room temperature is close to the acoustic photon wavelength and is much larger than their lattice constant. The scattering of

the thermal electron or hole can be dominated by the electron–acoustic phonon coupling at low-energy regime,48,56,57,58 which can be calculated by the DP theory proposed by Bardeen and

Shockley.18 On the basis of effective mass approximation, the carrier mobility (_µ_) for 3D materials can be expressed as $$\mu ^{3{\mathrm D}} = \frac{{2\sqrt {2\pi} e\hbar

^4C^{3{\mathrm{D}}}} }{{3(\kappa _{\mathrm B}T)^{3/2}m^{ \ast 5/2}E_1^2}},$$ (1) where _κ_B is the Boltzmann’s constant, _ћ_ is the Planck’s constant, _T_ is the temperature, and _C_3D is

the 3D elastic constant, defined as _C_3D = [_∂_2_E/∂δ_2]/_V_0 with _V_0 being the cell volume at equilibrium, _E_ is the total energy, and _δ_ is the applied uniaxial strain. _E_1 is the DP

constant proportional to the band edge shift induced by applied strain along the transport direction. _E_1 is defined as ∆_V__i_/(∆_l_/_l_0), where ∆_V__i_ is the energy change of the _i_th

band subject to lattice dilation ∆_l_/_l_0 along the transport direction (calculated with a step of 0.5%). _m_* is the effective mass in the transport direction and defined as _m_* = 

_ћ_2(_∂_2_ɛ_(_k_)_/∂k_2)−1, where _k_ is the wave-vector magnitude in momentum space. The anisotropic relaxation-time _τ_ can be calculated from the elastic constant _C_3D, the DP constant

_E_1 and the effective mass _m_*, as defined by _τ_ = _µm_*/_e_. The temperature used for the calculations of carrier mobility and relaxation-time is at room temperature (300 K). DATA

AVAILABILITY All data generated or analyzed during this study are included in this published article (and its supplementary information files). REFERENCES * Jeon, N. J. et al. Compositional

engineering of perovskite materials for high-performance solar cells. _Nature_ 517, 476 (2015). Article  CAS  Google Scholar  * Zhou, H. et al. Interface engineering of highly efficient

perovskite solar cells. _Science_ 345, 542–546 (2014). Article  CAS  Google Scholar  * Yang, W. S. et al. High-performance photovoltaic perovskite layers fabricated through intramolecular

exchange. _Science_ 348, 1234–1237 (2015). Article  CAS  Google Scholar  * Kojima, A. et al. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. _J. Am. Chem.

Soc._ 131, 6050–6051 (2009). Article  CAS  Google Scholar  * Best Research-Cell Efficiencies. http://www.nrel.gov/ncpv/images/efficiency_chart.jpg (Accessed March 2018). * Moehl, T. et al.

Strong photocurrent amplification in perovskite solar cells with a porous TiO2 blocking layer under reverse bias. _J. Phys. Chem. Lett._ 5, 3931–3936 (2014). Article  CAS  Google Scholar  *

Ravi, V. K. et al. Hierarchical arrays of cesium lead halide perovskite nanocrystals through electrophoretic deposition. _J. Am. Chem. Soc._ 140, 8887–8894 (2018). Article  CAS  Google

Scholar  * Liu, D. & Kelly, T. L. Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques. _Nat. Photonics_ 8, 133

(2014). Article  CAS  Google Scholar  * You, J. et al. Improved air stability of perovskite solar cells via solution-processed metal oxide transport layers. _Nat. Nanotech._ 11, 75 (2016).

Article  Google Scholar  * Son, D.-Y. et al. 11% efficient perovskite solar cell based on ZnO nanorods: an effective charge collection system. _J. Phys. Chem. C_ 118, 16567–16573 (2014).

Article  CAS  Google Scholar  * Zhu, Z. et al. Enhanced efficiency and stability of inverted perovskite solar cells using highly crystalline SnO2 nanocrystals as the robust

electron‐transporting layer. _Adv. Mater_. 28, 6478–6484 (2016). * Wang, K. et al. Low-temperature and solution-processed amorphous WOX as electron-selective layer for perovskite solar

cells. _J. Phys. Chem. Lett._ 6, 755–759 (2015). Article  CAS  Google Scholar  * Wojciechowski, K. et al. C60 as an efficient n-type compact layer in perovskite solar cells. _J. Phys. Chem.

Lett._ 6, 2399–2405 (2015). Article  CAS  Google Scholar  * Seo, J. et al. Benefits of very thin PCBM and LiF layers for solution-processed p–i–n perovskite solar cells. _Energy Environ.

Sci._ 7, 2642–2646 (2014). Article  CAS  Google Scholar  * Jeng, J. Y. et al. Nickel oxide electrode interlayer in CH3NH3PbI3 perovskite/PCBM planar‐heterojunction hybrid solar cells. _Adv.

Mater._ 26, 4107–4113 (2014). Article  CAS  Google Scholar  * Sheng, X.-L. et al. T-carbon: a novel carbon allotrope. _Phys. Rev. Lett._ 106, 155703 (2011). Article  Google Scholar  * Zhang,

J. et al. Pseudo-topotactic conversion of carbon nanotubes to T-carbon nanowires under picosecond laser irradiation in methanol. _Nat. Commun._ 8, 683 (2017). Article  Google Scholar  *

Bardeen, J. & Shockley, W. Deformation potentials and mobilities in non-polar crystals. _Phys. Rev._ 80, 72 (1950). Article  CAS  Google Scholar  * Csonka, G. I. et al. Assessing the

performance of recent density functionals for bulk solids. _Phys. Rev. B_ 79, 155107 (2009). Article  Google Scholar  * Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based

on a screened Coulomb potential. _J. Chem. Phys._ 118, 8207–8215 (2003). Article  CAS  Google Scholar  * Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals

applied to solids. _Phys. Rev. B_ 83, 195131 (2011). Article  Google Scholar  * Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional.

_J. Phys. Condens. Mater._ 22, 022201 (2009). Article  Google Scholar  * Lee, K. et al. Higher-accuracy van der Waals density functional. _Phys. Rev. B_ 82, 081101 (2010). Article  Google

Scholar  * Grimme, S. Semiempirical GGA‐type density functional constructed with a long‐range dispersion correction. _J. Comput. Chem._ 27, 1787–1799 (2006). Article  CAS  Google Scholar  *

Vidal, J. et al. Effects of electronic and lattice polarization on the band structure of delafossite transparent conductive oxides. _Phys. Rev. Lett._ 104, 136401 (2010). Article  Google

Scholar  * Körner, W. et al. Prediction of subgap states in Zn-and Sn-based oxides using various exchange-correlation functionals. _Phys. Rev. B_ 90, 195142 (2014). Article  Google Scholar 

* Lazar, P. et al. The nature of bonding and electronic properties of graphene and benzene with iridium adatoms. _Phys. Chem. Chem. Phys._ 16, 20818–20827 (2014). Article  CAS  Google

Scholar  * Li, T. et al. Phase stability and electronic structure of prospective Sb-based mixed sulfide and iodide 3D perovskite (CH3NH3)SbSI2. _J. Phys. Chem. Lett._ 9, 3829–3833 (2018).

Article  CAS  Google Scholar  * Zhou, Z. et al. Interface engineering for high-performance perovskite hybrid solar cells. _J. Mater. Chem. A_ 3, 19205–19217 (2015). Article  CAS  Google

Scholar  * Rao, H. S. et al. Improving the extraction of photogenerated electrons with SnO2 nanocolloids for efficient planar perovskite solar cells. _Adv. Funct. Mater._ 25, 7200–7207

(2015). Article  CAS  Google Scholar  * Yang, D. et al. High efficiency planar-type perovskite solar cells with negligible hysteresis using EDTA-complexed SnO2. _Nat. Commun._ 9, 3239

(2018). Article  Google Scholar  * Li, S. et al. Interface engineering of high efficiency perovskite solar cells based on ZnO nanorods using atomic layer deposition. _Nano Res._ 10,

1092–1103 (2017). Article  CAS  Google Scholar  * Xiong, L. et al. Fully high‐temperature‐processed SnO2 as blocking layer and scaffold for efficient, stable, and hysteresis‐free mesoporous

perovskite solar cells. _Adv. Funct. Mater._ 28, 1706276 (2018). Article  Google Scholar  * Yang, G. et al. Reducing hysteresis and enhancing performance of perovskite solar cells using

low‐temperature processed Y‐doped SnO2 nanosheets as electron selective layers. _Small_ 13, 1601769 (2017). Article  Google Scholar  * Choi, K. et al. Thermally stable, planar hybrid

perovskite solar cells with high efficiency. _Energy Environ. Sci._ https://doi.org/10.1039/C8EE02242A (2018). Article  Google Scholar  * Chou, H.-H. et al. Zinc porphyrin–ethynylaniline

conjugates as novel hole-transporting materials for perovskite solar cells with power conversion efficiency of 16.6%. _ACS Energy Lett._ 1, 956–962 (2016). Article  CAS  Google Scholar  *

Frisch, M. et al. _Gaussian 16, Revision A. 03._ (Gaussian Inc., Wallingford CT, 2016). Google Scholar  * O’regan, B. & Grätzel, M. A low-cost, high-efficiency solar cell based on

dye-sensitized colloidal TiO2 films. _Nature_ 353, 737 (1991). Article  Google Scholar  * Ke, W. et al. Perovskite solar cell with an efficient TiO2 compact film. _ACS Appl. Mater.

Interfaces_ 6, 15959–15965 (2014). Article  CAS  Google Scholar  * Burschka, J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. _Nature_ 499,

316 (2013). Article  CAS  Google Scholar  * Tan, Z.-K. et al. Bright light-emitting diodes based on organometal halide perovskite. _Nat. Nanotechnol._ 9, 687–692 (2014). Article  CAS  Google

Scholar  * Xiong, L. et al. Performance enhancement of high temperature SnO2-based planar perovskite solar cells: electrical characterization and understanding of the mechanism. _J. Mater.

Chem. A_ 4, 8374–8383 (2016). Article  CAS  Google Scholar  * Umari, P., Mosconi, E. & De Angelis, F. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell

applications. _Sci. Rep._ 4, 4467 (2014). Article  Google Scholar  * Qiao, J. et al. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. _Nat. Commun._ 5,

4475 (2014). Article  CAS  Google Scholar  * Ma, Y., Kuc, A. & Heine, T. Single-layer Tl2O: a metal-shrouded 2D semiconductor with high electronic mobility. _J. Am. Chem. Soc._ 139,

11694–11697 (2017). Article  CAS  Google Scholar  * Murphy-Armando, F. & Fahy, S. First-principles calculation of carrier-phonon scattering in n-type Si1−xGex alloys. _Phys. Rev. B_ 78,

035202 (2008). Article  Google Scholar  * Tiwana, P. et al. Electron mobility and injection dynamics in mesoporous ZnO, SnO2, and TiO2 films used in dye-sensitized solar cells. _ACS Nano_ 5,

5158–5166 (2011). Article  CAS  Google Scholar  * Cai, Y., Zhang, G. & Zhang, Y.-W. Polarity-reversed robust carrier mobility in monolayer MoS2 nanoribbons. _J. Am. Chem. Soc._ 136,

6269–6275 (2014). Article  CAS  Google Scholar  * Oga, H. et al. Improved understanding of the electronic and energetic jandscapes of perovskite solar cells: high local charge carrier

mobility, reduced recombination, and extremely shallow traps. _J. Am. Chem. Soc._ 136, 13818–13825 (2014). Article  CAS  Google Scholar  * Motta, C., El-Mellouhi, F. & Sanvito, S. Charge

carrier mobility in hybrid halide perovskites. _Sci. Rep._ 5, 12746 (2015). Article  CAS  Google Scholar  * Yang, D. et al. Surface optimization to eliminate hysteresis for record

efficiency planar perovskite solar cells. _Energy Environ. Sci._ 9, 3071–3078 (2016). Article  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient

approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996). Article  CAS  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953 (1994). Article  Google

Scholar  * Román-Pérez, G. & Soler, J. M. Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes. _Phys. Rev. Lett._ 103, 096102

(2009). Article  Google Scholar  * Dion, M. et al. Van der Waals density functional for general geometries. _Phys. Rev. Lett._ 92, 246401 (2004). Article  CAS  Google Scholar  * Kaasbjerg,

K., Thygesen, K. S. & Jacobsen, K. W. Phonon-limited mobility in n-type single-layer MoS2 from first principles. _Phys. Rev. B_ 85, 115317 (2012). Article  Google Scholar  * Kaasbjerg,

K., Thygesen, K. S. & Jauho, A.-P. Acoustic phonon limited mobility in two-dimensional semiconductors: deformation potential and piezoelectric scattering in monolayer MoS2 from first

principles. _Phys. Rev. B_ 87, 235312 (2013). Article  Google Scholar  * Long, M.-Q. et al. Theoretical predictions of size-dependent carrier mobility and polarity in graphene. _J. Am. Chem.

Soc._ 131, 17728–17729 (2009). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors gratefully acknowledge financial support from Ministry of Education, Singapore

(Academic Research Fund TIER 1-RG128/14) and by Economic Development Board of Singapore and Infineon Technologies Asia Pacific Pte Ltd. through the Industrial Postgraduate Programme, Nanyang

Technological University, Singapore. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * School of Mechanical and Aerospace Engineering, Nanyang Technological University, 50 Nanyang Avenue,

Singapore, 639798, Singapore Ping-Ping Sun, Lichun Bai, Devesh R. Kripalani & Kun Zhou * SMRT-NTU Smart Urban Rail Corporate Laboratory, Nanyang Technological University, 50 Nanyang

Avenue, Singapore, 639798, Singapore Lichun Bai & Kun Zhou Authors * Ping-Ping Sun View author publications You can also search for this author inPubMed Google Scholar * Lichun Bai View

author publications You can also search for this author inPubMed Google Scholar * Devesh R. Kripalani View author publications You can also search for this author inPubMed Google Scholar *

Kun Zhou View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS P.-P.S. and K.Z. conceived and designed the project. P.-P.S. performed the DFT

calculations and related analysis. P.-P.S., L.B., D.R.K., and K.Z. analyzed the results. P.-P.S. wrote the manuscript, L.B., D.R.K., and K.Z. helped to revise the manuscript. All authors

discussed and commented on the manuscript. CORRESPONDING AUTHOR Correspondence to Kun Zhou. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL

INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Sun, PP., Bai, L., Kripalani, D.R. _et al._ A new carbon phase with direct bandgap and high carrier mobility as electron transport material for perovskite solar cells. _npj Comput

Mater_ 5, 9 (2019). https://doi.org/10.1038/s41524-018-0146-z Download citation * Received: 18 July 2018 * Accepted: 13 December 2018 * Published: 15 January 2019 * DOI:

https://doi.org/10.1038/s41524-018-0146-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative