120 gops photonic tensor core in thin-film lithium niobate for inference and in situ training

ABSTRACT Photonics offers a transformative approach to artificial intelligence (AI) and neuromorphic computing by enabling low-latency, high-speed, and energy-efficient computations.

However, conventional photonic tensor cores face significant challenges in constructing large-scale photonic neuromorphic networks. Here, we propose a fully integrated photonic tensor core,

consisting of only two thin-film lithium niobate (TFLN) modulators, a III-V laser, and a charge-integration photoreceiver. Despite its simple architecture, it is capable of implementing an

entire layer of a neural network with a computational speed of 120 GOPS, while also allowing flexible adjustment of the number of inputs (fan-in) and outputs (fan-out). Our tensor core

supports rapid in-situ training with a weight update speed of 60 GHz. Furthermore, it successfully classifies (supervised learning) and clusters (unsupervised learning) 112  × 112-pixel

images through in-situ training. To enable in-situ training for clustering AI tasks, we offer a solution for performing multiplications between two negative numbers. SIMILAR CONTENT BEING

VIEWED BY OTHERS SINGLE-CHIP PHOTONIC DEEP NEURAL NETWORK WITH FORWARD-ONLY TRAINING Article 02 December 2024 DEEP LEARNING WITH PHOTONIC NEURAL CELLULAR AUTOMATA Article Open access 08

October 2024 FULLY FORWARD MODE TRAINING FOR OPTICAL NEURAL NETWORKS Article Open access 07 August 2024 INTRODUCTION Artificial intelligence (AI) is increasingly being integrated into

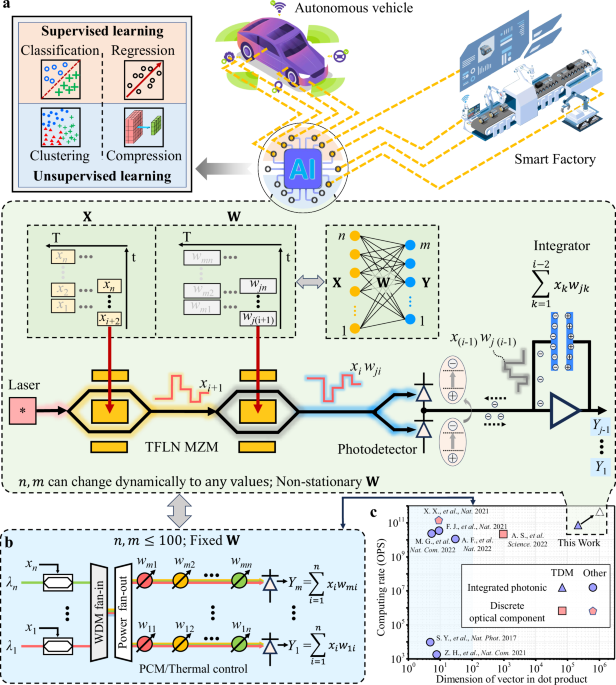
various sectors, including autonomous vehicles, smart buildings, and smart factories, as illustrated in Fig. 1a. At the heart of AI systems are tensor core processors, which are expected to

exhibit several key characteristics: * (1) High-speed, large-scale matrix-vector multiplication: These processors must efficiently process data from a variety of devices for tasks such as

classification (supervised learning) and clustering (unsupervised learning), as depicted in Fig. 1a. Crucially, they perform matrix-vector multiplication and dynamically adjust the input

(fan-in) and output (fan-out) sizes of each network layer as needed. * (2) Rapid weight updates: Accurate and efficient training necessitates the use of in situ training1,2,3,4. This method

incorporates real-time feedback from processors into the weight update loop, accounting for processor imperfections and environmental changes. Rapid weight updates speed up training and

facilitate “on-the-fly” or online learning, which is particularly beneficial for applications such as autonomous vehicles5. * (3) Low energy consumption and compact form factor: AI systems

often deploy multiple processors (see Fig. 1a), so these processors must be energy-efficient and compact to facilitate widespread integration. However, finding a tensor core processor that

meets all these requirements simultaneously is challenging6,7,8,9,10,11,12,13,14. Traditional digital computers struggle with the speed and energy efficiency required for matrix algebra due

to Joule heating, electromagnetic crosstalk, and parasitic capacitance15,16. In contrast, photonic integrated circuits (PICs)-based tensor core processors provide high computational speed,

low energy consumption, and compactness, effectively overcoming these issues15,17,18,19. Nonetheless, developing an integrated photonic tensor core (IPTC) capable of large-scale

matrix-vector multiplication with adjustable input (fan-in) and output (fan-out) sizes, alongside rapid weight updates, remains a significant challenge. For example, IPTCs utilizing

wavelength-division multiplexing (WDM) are inherently limited by the number of available wavelength channels, which constrains the fan-in size in a neural network layer (see Fig. 1b)13,20.

In addition, IPTCs based on interferometric meshes8,18 require a single laser source but face scalability issues due to the multitude of directional couplers and phase shifters involved. To

date, most IPTCs have been limited to using either static (non-volatile) weights, such as those employing phase change materials15,21, or volatile weights based on thermo-optic effects [18],

which are slow and power inefficient. These methods are unsuitable for in situ training22. Although some IPTC models that utilize two cascaded modulators can achieve rapid weight updates,

they still require summing in the digital domain, which strongly limits the final computational speed, or they need 2N modulators for performing dot product operations on two N-dimensional

vectors23,24,25,26. Recently, a solution first proposed by De Marinis et al.27, which uses photocurrent integrators to perform accumulation operations in a time-division multiplexing (TDM)

scheme, has been gaining attention28,29. Here, we introduce an IPTC with thin-film lithium niobate (TFLN) photonics and charge-integration photoreceivers (Fig. 1b), combining the advantages

of photonics and analog electronics. Our processor can perform large-scale matrix-vector multiplications at high computational speeds9,10,11,15,18,28,30, as quantified in Fig. 1c. This fully

integrated processor, comprises only two TFLN modulators, an III–V laser, and a charge-integration photoreceiver (Fig. 1b). By adjusting the integration time of the charge-integration

photoreceiver, we can flexibly modify the fan-in size for matrix-vector multiplications. Our processor can handle a fan-in size of 131,072–significantly surpassing the capacity of previously

reported IPTCs by four orders of magnitude (Fig. 1c). Leveraging the high modulation speed of TFLN modulators and the fast accumulation operation of charge-integration

photoreceivers31,32,33, our tensor core achieves a computational speed of 120 GOPS. Moreover, with a weight update speed of 60 GHz, our tensor core enables fast in situ training. Our device

successfully classifies (supervised learning) and clusters (unsupervised learning) 112 × 112-pixel images via in situ training. Notably, to the best knowledge, our device is the first to

provide a solution for performing multiplications between two negative numbers, thanks to the ability of TFLN modulators to operate across a wide wavelength range. Thus, our device is the

first one capable of performing in situ training for clustering images. For compactness, our tensor core employs hybrid integration techniques to combine the TFLN chip with III–V lasers and

photodetectors34,35. RESULTS CONCEPT AND PRINCIPLE Figure 1a presents a schematic of the proposed TDM-based IPTC, consisting of two cascaded TFLN Mach-Zehnder modulators, one laser, and one

charge-integration photoreceiver. Our device uses charge-integration photoreceivers for accumulative operations and leverages TFLN Mach-Zehnder modulators for high-speed multiplication

operations and weight updates. Therefore, using just four physical components, our IPTC can implement an entire layer of a neural network with _n_ fan-in and _m_ fan-out. _n_ and _m_ can be

dynamically adjusted as needed. In contrast, the conventional WDM-based IPTC requires _n_ modulators, _n_ × _m_ weight additions, and _m_ large-bandwidth photodetectors to implement a layer

with _n_ fan-in and _m_ fan-out (see Fig. 1b). The input data is flattened into a vector and modulated on a time basis becoming \(X(t)={\sum }_{j=1}^{n}{x}_{j}\int_{0}^{\infty }\delta

(t-j/{f}_{s})\,{{\rm{d}}}t\), where _n_ is the dimension of the input vector, _δ_ is the Dirac delta function, and _f__s_ is the baud rate of the modulator. Simultaneously, the weights of

the _i__t__h_ row are flattened into a vector becoming \({W}_{i}(t)=\mathop{\sum }_{j=1}^{n}{w}_{ij}\int_{0}^{\infty }\delta (t-j/{f}_{s}+\Delta T)\,{{\rm{d}}}t\), where _Δ__T_ is a delay

time that needs to be calibrated to guarantee each weight vector element can be correctly multiplied by the corresponding element of the input vector. At a time, _t_, _x__j_ is modulated by

_w__i__j_ performing the multiplying operation of the _j__t__h_ element. In this way, the multiplication of all of the elements of _X_(_t_) and _W__i_(_t_) are multiplied sequentially and

then summed by the integrator. Therefore, the dot product operation between the input and weight vectors, \({Y}_{i}=\mathop{\sum }_{j=1}^{n}{x}_{j}{w}_{ij}\), can be obtained by simply

reading the output voltage of the integrator through an analog-to-digital converter whose sampling rate only needs to be _f__s_/_n_. By adjusting the integration time of the integrator, _n_

can be changed and made to be very large. By computing the output of each node sequentially in a time series, our device can implement an entire layer of a neural network. Therefore, our

processor can offer the flexibility to dynamically change the sizes of fan-in and fan-out in a layer. Moreover, through this architecture, our device can perform fast in situ training

because it can update the weight vectors at the modulation speed of the modulator. PROTOTYPE Figure 2a presents a photo of a prototype of our device. In addition, Fig. 2b–e provides

zoomed-in micrographs of the fabricated TFLN chip, flip-chip photodetectors, traveling-wave electrodes of the modulator, and laser, respectively. More details regarding the fabrication of

the TFLN chip can be found in Methods. Using flip-chip bonding technology, two photodetectors (marked as PD1 and PD2), in a balanced detection scheme, were affixed above two grating

couplers, as shown in Fig. 2c. The laser and TFLN chip were connected using a photonic wire bond whose shape can be adapted to match the actual positions of the waveguide facets (see Fig. 

2e). As shown in the right side of Fig. 2c, we also connected our TFLN chip with a fiber array by photonic wire bonds for calibrating bias voltages and delay time, and assisting in the

multiplication involving two negative numbers. Details regarding the photonic wire bonding technology are shown in Methods and Supplementary Note 1. Figure 2f illustrates the relative

heights of the TFLN chip, laser, and photodetectors. Figure 2g presents the light-current-voltage (L-I-V) curves for the light coupled into the TFLN chip from the laser with a wavelength of

1307.22 nm. More detailed performances of the hybrid integrated laser are shown in Supplementary Note 2. Thanks to the periodic capacitively loaded traveling-wave electrodes (see Fig. 

2d)32,36,37, the 3-dB electro-optic bandwidth of our modulator is broader than 60 GHz (see Fig. 2h). The output voltage of the integrator linearly increases with the integration time for a

constant input optical power (see Fig. 2i). In a balanced detection scheme, when the optical power received by PD1 is lower than that received by PD2, the output voltage variation of the

integrator is positive and, when it is higher than that received by PD2, the output voltage variation of the integrator is negative. This means that the proposed photoreceiver can perform

add and subtract operations in the matrix-vector multiplication. More details regarding the charge integrator and the corresponding electrical controlling circuit can be found in

Supplementary Note 3. DOT PRODUCT ACCELERATOR In this section, we demonstrate how to perform a dot product operation between two vectors using our device. A schematic of data flows through

our device is shown in Fig. 3a. Python, an open-source programming language, was used to control all our devices. We recorded 3780 photonic dot product measurements using our device by

randomly varying the two vectors. The dimension of each vector was set at 131072, a limit imposed by our high-speed arbitrary waveform generator (AWG). The two vectors were modulated

separately by two modulators at a modulation rate of 60 Gbaud, enabling a computational speed of 120 GOPS, and a weight update speed of 60 GHz. The time delay between two vectors was

initially calibrated to guarantee that each element of the first vector can be correctly multiplied by the corresponding element of the second vector. More details regarding the experimental

setup can be found in Supplementary Note 4. The measured output voltage (_i.e_., dot product result), scaled between  − 1 and  + 1, as a function of the expected dot product result, is

shown in Fig. 3b. Compared with the expected dot product result, the error of the measured one has a standard deviation of 0.03 (6.04 bits)–more than the 4 bits of precision required for

performing AI tasks (details can be found in Supplementary Note 4)38. IMAGES CLASSIFICATION We built a multilayer perceptron (see Fig. 4a) and tested it against the MNIST large-scale

handwritten digit database39,40. Here, the multilayer perceptron includes 4 layers: an input layer, two hidden layers, and an output layer. Each handwritten digit image, having 112 × 112

pixels, was flattened into a 12544 × 1 vector as the input of the first layer. The number of nodes in the first and second hidden layers was set to 70 and 300, respectively, and the leaky

ReLU function was used for the nonlinear activation function41. Classification is a supervised learning AI task that requires labeled data to train the model. Our multilayer perceptron model

was trained with 2000 labeled digit images using an in situ training scheme (see Fig. 4b) that our IPTC performs forward propagation. At the same time, the electronic computer handles

nonlinearity function and backpropagation. Weight vectors were updated by the stochastic gradient descent method42, allowing individual samples to be trained iteratively. The training

process from forward propagation to backpropagation was repeated until convergence. Figure 4c shows the validation accuracy as a function of epoch for in situ training scheme compared to

that running on just a central processing unit (CPU). More details regarding the training algorithm and the interfaces between the central processing unit (CPU) and the optoelectronic

assembly can be found in the Methods and Supplementary Note 4. The confusion matrix for 500 images (Fig. 4d, e) shows an accuracy of 91.8 % for the generated predictions, in contrast to 92%

for the numerical results calculated on a CPU. Our IPTC achieved near theoretical accuracy, indicating that the in situ training scheme enables the system to inherently account for the

hardware nonidealities, including fabrication variations and noise. Essentially, the nonidealities are “baked into” the training process. This has also been experimentally demonstrated in

ref. 3. IMAGES CLUSTERING Supervised learning can successfully solve real-world challenges, but it has some drawbacks. One of the main limitations is that it requires a large number of

accurately labeled data to train the model43,44. Creating such a database is a time-consuming and resource-intensive task that may not always be feasible. In contrast, unsupervised learning

can be operated on unlabeled data to discover its underlying structure, offering an alternative approach for extracting data features. We demonstrate the potential of our device for

unsupervised learning AI tasks by utilizing it to cluster the MNIST large-scale handwritten digits with principle component analysis — one of the most commonly used unsupervised learning

models45. Principle component analysis simplifies high-dimensional data by geometrically projecting them onto a limited number of principal components (PCs), _i.e_., unit vectors, to obtain

the best summary of the data45. Clustering handwritten digits with principle component analysis involves two main steps: (1) finding the PCs for the unlabeled database, _i.e_., training the

model, and (2) projecting the data onto each PC. Here, we used the power method to find the PCs that46 $${{{\bf{b}}}}_{i+1}=\frac{{{\bf{A}}}{{{\bf{b}}}}_{i}}{\parallel

{{\bf{A}}}{{{\bf{b}}}}_{i}\parallel },$$ (1) where A = XTX, XT means the transpose of X, X is a _p_ × _n_ data matrix with column-wise zero empirical mean, and _p_ and _n_ are the total

number of handwritten digits and the pixels of each digit, respectively. B_i_ is a _n_ × 1 unit vector, obtained at the _i__t__h_ iteration, and B0 is a randomly generated unit vector. B_i_

converges to the first PC (PC1) when the variance of the projected points, XB_i_, achieves the maximum value. The subsequent PCs can be obtained by a similar approach after subtracting all

the previous PCs from X. More details regarding the power method can be found in Methods. Through Eq. (1), we can know that the training involves the multiplication between two negative

numbers. To achieve this, as illustrated in Fig. 5a, we found a solution that injects light with a wavelength of _λ_2 into the second modulator, in addition to injecting light with a

wavelength of _λ_1 into the first modulator. When the phase difference between the two arms of the first and second modulators is adjusted to _θ_1 and _θ_2, respectively, the output of the

balanced photodetectors becomes \({I}_{0}\sin {\theta }_{1}\sin {\theta }_{2}\), indicating that this method enables the multiplication between two numbers with any signs. More details

regarding the working principle can be found in Supplementary Note 4. The convergence speed of our device is comparable with that of the CPU (see Fig. 5b), demonstrating that a dot product

computing precision of 6.04 bits is enough to train the model using the power method. Using the power method discussed above, we can obtain all the principal components. However, in general,

the first few PCs are sufficient to summarize the data. In our example, the projections onto PC1-PC44 encompass 90% of the features. To visualize the clustering result of the handwritten

digits using our device, Fig. 5c and d present the projections onto PC1-PC3, accounting for 28.7% of the features. Although only the first three PCs are used, the unlabeled handwritten

digits can still be well clustered. Moreover, projecting the data onto the three PCs using our device is 5 times faster than a CPU (Intel i9-9900 @ 3.10 GHz). TDM AND WDM-BASED ARCHITECTURE

To show the scalability of our solution, we propose an end-to-end photonic neural network that combines the benefits of TDM and WDM methods, as illustrated in Fig. 6. This network is capable

of executing multiple AI tasks simultaneously, spanning from the input to the output layer, with nanoseconds latency, all without relying on a digital processor for assistance. As an

example, shown in Fig. 6, is a proposed neural network that includes 4 layers: an input layer, two hidden layers, and an output layer. (1) From the input layer to the hidden layer 1. The

information of _K_ AI tasks is encoded by _K_ input TFLN modulators and transmitted on _K_ corresponding wavelengths. These signals from input TFLN modulators are then split and channeled

into _m-_weighted TFLN modulators. Although some waveguides must pass through (_K_ − 1) crossings, the total insertion losses remain manageable, as an insertion loss of 0.02 dB per crossing

has been demonstrated47. Following this, each weighted TFLN modulator feeds into a _K_-channel WDM, which separates the wavelengths to _K_ charge-integration photoreceivers for generating

vector-vector dot products. _K_ commercial complementary metal-oxide-semiconductor (CMOS) switches48 control the output timings of these photoreceivers. In addition, a CMOS comparator, which

selects the maximum between the input and reference voltages, facilitates the ReLU activation function of each vector vector dot product49. The use of 90 wavelengths from a comb source for

photonic neural networks30 and a 64-channel integrated WDM50 have been previously demonstrated, making _K_, _m_ = 64 a practical choice. With this setup, we can achieve a computational speed

of 491 TOPS and an energy efficiency of 6.5 fJ/OP (_i.e_., 153 TOPS/W), factoring in a modulation speed of 60 Gbaud/s, including the energy consumption of the laser, DACs,

charge-integration photoreceivers, CMOS switches, and CMOS comparators. Further details are available in Supplementary Note 6. (2) From hidden layer 1 to 2, and from hidden layer 2 to the

output layer, conventional WDM-based architectures3,15 are employed. These parts are unaffected by limitations related to fan-in size, thanks to the relatively small numbers of nodes in the

hidden layers. The outputs of hidden layer 1 are fully connected to the _m_ neurons in hidden layer 2. Similarly, the _h_ outputs from hidden layer 2 are fully connected to the _p_ neurons

of the output layer, resulting in _p_ network outputs. This hybrid processor enables the sequential processing of 64 images, each with a resolution of 112 × 112 pixels, within 62.5 ns. Its

significant potential extends to various fields, including autonomous vehicles requiring simultaneous image processing from multiple cameras. DISCUSSION Our device’s computational speed,

compactness, and ability for large-scale dot product operations are summarized in Fig. 1c, where the performance of our device is compared to that of other state-of-the-art photonic

devices9,10,11,15,18,28,30. Our device can simultaneously achieve high performance across all these aspects. Note that “ability” refers to our processor to perform dot product operations

without the assistance of a digital processor for accumulation operations. According to the demonstrated performance of the TFLN modulator51, our IPTC can achieve a computational speed of

over 520 GOPS, and the vector dimension can extend to over one million (the dotted triangle shown in Fig. 1c) using more advanced modulator driver boasting higher speeds and larger memory

capacity. Compared to photonic processors based on free-space52 or discrete30 optics, our fully integrated processor is compact. However, the footprint of fast modulators is not the primary

reason for choosing the TFLN technology. The size of high-speed drivers, often the bottleneck in achieving an ultra-high compute density, must also be considered. Our choice of TFLN

modulators is driven by their ability to: (1) simultaneously achieve a low insertion loss, CMOS-compatible voltage, and a broad electro-optic bandwidth32. (2) Operate across a wide

wavelength range, perform multiplication of two negative numbers, and for their compatibility with hybrid TDM and WDM architectures, as previously discussed, and (3) exhibit no modulation

loss, unlike silicon modulators, which suffer from variable insertion loss depending on the applied voltage. In summary, we have experimentally demonstrated that our device can perform

large-scale matrix-vector multiplications with flexibly adjustable fan-in and fan-out sizes and facilitate rapid weight updates. Our device is the pioneering IPTC with the capability to

handle the multiplication between two negative numbers. It is capable of processing both supervised and unsupervised learning AI tasks through in situ training. Thanks to its compatibility

with current commercial optical transceivers, our solution has the potential to rapidly enter the commercial phase. By taking advantage of electronic and photonic analog computing, our

research paves the way for developing a universal IPTC. METHODS DESIGN AND FABRICATION OF TFLN CHIP The proposed TFLN chip was fabricated using a wafer (NanoLN) consisting of a 360 nm thick,

x-cut, y-propagating, LN thin film on a 500 μm thick quartz handle with a 2 μm SiO2 layer in between the two. The optical devices were patterned using optical lithography and etched using

inductively coupled plasma. Then, a cladding layer with a 1 μm thick SiO2 was deposited on the top of optical devices. Gold and heater electrodes were then patterned with a lift-off process.

To achieve a low-voltage, high-bandwidth electro-optic solution, we used 1 cm-long, capacitively loaded, traveling-wave electrodes on our TFLN modulators. Our modulators exhibit a 3-dB

electro-optic bandwidth broader than 67 GHz, a V_π_ of 2.4 V, and an extinction ratio larger than 20 dB. For the TDM and WDM-based architecture, We note that during the review process of

this paper, other teams were developing similar schemes, which constitute the first part of the photonic neural network shown in Fig. 6, using bulk fiber-optic modulators, with results

presented in conference proceedings25,26. PHOTONIC WIRE BONDING PROCESS Photonic wire bonding is a technique for building hybrid connections between disparate optical components, such as

TFLN chips, lasers, and fiber arrays, using three-dimensional (3D) polymer waveguides created by in situ, two-photon polymerization53. In our case, the photonic wire bonds were used between

the TFLN chip and the laser. We also used the photonic wire bonds in various locations of our hybrid photonic circuit for calibration and testing purposes. The hybridization process was

carried out as follows: first, the TFLN chip, a fiber array (used in calibration and testing), and the laser were glued to an aluminum submount with a low alignment precision using

ultraviolet curable epoxies; second, the photoresist was dispensed on the optical ports of the TFLN chip, fiber array, and laser; third, the photonic wire bonder (Vanguard Automation GmbH,

SONATA1000) was used to expose the photoresist and develop the shape of the interconnecting photonic wires. More detailed performances of photonic wire bonds and the hybrid integrated laser

are shown in Supplementary Note 2. EXPERIMENTAL SETUP A vector network analyzer (Agilent N5227A) with a bandwidth of up to 67 GHz was used to characterize the electro-optic response of the

fabricated modulator at a telecom wavelength of 1310 nm. To perform the dot product operation, our device was driven by an arbitrary wave generator (Keysight, M8194A). For comparison

purposes, the machine learning algorithms are also executed using a CPU (Intel i9-9900 @ 3.10GHz). More details can be found in Supplementary Note 4. THE PRINCIPLE OF THE STOCHASTIC GRADIENT

DESCENT METHOD For the multilayer perceptron, the weight vectors in this study were updated using the stochastic gradient descent method, allowing individual samples to be trained

iteratively. The training was implemented using a labeled dataset (X, T), where X is the network input, and T is the target to be compared with the network output. In the forward

propagation, the output vector, Z(_l_), of the _l__t__h_ layer can be given by $${{{\bf{z}}}}^{(l)}={{{\bf{w}}}}^{(l)}\cdot g({{{\bf{z}}}}^{(l-1)}),$$ (2) where W(_l_) represents the weight

matrix between the (_l_−1)_t__h_ and (_l_)_t__h_ layers, _g_(Z(_l_−1)) is the activation function for the output of the \(\left.\right({(l-1)}^{th}\) layer, and Z(1) = X. Through

backpropagation, the “error”, Δ(_l_−1), of the (_l_−1)_t__h_ layer can be calculated by $${{{\mathbf{\delta }}}}^{(l)}={({{{\bf{w}}}}^{(l)})}^{{{\rm{T}}}}\cdot {{{\mathbf{\delta

}}}}^{(l+1)},$$ (3) where \({({{{\bf{w}}}}^{(l)})}^{T}\) means the transpose of W(_l_), and Δ(4) = (T − Z(4)) in the case of our network only has 4 layers. Then, the weight matrix can be

updated by $${{{\bf{w}}}}^{(l)}={{{\bf{w}}}}^{(l)}+\Delta {{{\bf{w}}}}^{(l)},$$ (4) where \(\Delta {{{\bf{w}}}}^{(l)}=\gamma ({{{\mathbf{\delta }}}}^{(l+1)}\odot

g({{{\bf{z}}}}^{(l+1)}))\cdot {({{{\bf{z}}}}^{(l)})}^{{{\rm{T}}}},\gamma\) is the learning rate, and ⊙ is the Hadamard product (element-wise multiplication operator). In our “in situ"

training scheme, our IPTC performed forward propagation while the computer handled nonlinearity function and backpropagation. This training process from forward propagation to

backpropagation was repeated until convergence or all samples were trained. THE PRINCIPLE OF POWER METHOD FOR FINDING ALL PRINCIPLE COMPONENTS We can find each PC by repeating Eq. (1), but

the matrix A needs to be changed for different PCs. To find the kth PC, W(_k_), the matrix A can be given by $${{\bf{A}}}={\hat{{{\bf{X}}}}}_{k}^{{\bf{T}}}{\hat{{{\bf{X}}}}}_{k},$$ (5) where

$${\hat{{{\bf{X}}}}}_{k}={{\bf{X}}}-\sum_{s=1}^{k-1}{{\bf{X}}}{{{\bf{w}}}}_{(s)}{{{\bf{w}}}}_{(s)}^{{\mathsf{T}}}$$ (6) X is a _p_ × _n_ data matrix with column-wise zero empirical mean,

_p_ and _n_ are the number of samples and the pixels of each digit image, respectively. W(_s_) means the s_t__h_ PC. DATA AVAILABILITY The authors declare that the data supporting the

findings of this study are available within the paper and its Supplementary Information files. Source data can be found at https://doi.org/10.6084/m9.figshare.26965324. CODE AVAILABILITY The

code used in this study is available from the corresponding authors upon reasonable request. REFERENCES * Pai, S. et al. Experimentally realized in situ backpropagation for deep learning in

photonic neural networks. _Science_ 380, 398–404 (2023). Article  ADS  CAS  PubMed  Google Scholar  * Buckley, S.M., Tait, A.N., McCaughan, A.N. & Shastri, B.J. Photonic online

learning: a perspective. Nanophotonics 12, https://doi.org/10.1515/nanoph-2022-0553 (2023). * Filipovich, M. J. et al. Silicon photonic architecture for training deep neural networks with

direct feedback alignment. _Optica_ 9, 1323–1332 (2022). Article  ADS  CAS  Google Scholar  * Huang, C. et al. A silicon photonic–electronic neural network for fibre nonlinearity

compensation. _Nat. Electron._ 4, 837–844 (2021). Article  CAS  Google Scholar  * Pan, Y. et al. Imitation learning for agile autonomous driving. _Int. J. Robot. Res._ 39, 286–302 (2020).

Article  Google Scholar  * Lee, J. et al. UNPU: An energy-efficient deep neural network accelerator with fully variable weight bit precision. _IEEE J. Solid State Circuits_ 54, 173–185

(2018). Article  ADS  Google Scholar  * Mythic M1076 Analog matrix processor. https://mythic.ai/products/m1076-analog-matrix-processor/ (2022). * Fu, T. et al. Photonic machine learning with

on-chip diffractive optics. _Nat. Commun._ 14, 70 (2023). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Mourgias-Alexandris, G. et al. Noise-resilient and high-speed deep

learning with coherent silicon photonics. _Nat. Commun._ 13, 5572 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ashtiani, F., Geers, A. J. & Aflatouni, F. An

on-chip photonic deep neural network for image classification. _Nature_ 606, 501–506 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Zhang, H. et al. An optical neural chip for

implementing complex-valued neural network. _Nat. Commun._ 12, 457 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Thakur, C. S. et al. Large-scale neuromorphic spiking

array processors: A quest to mimic the brain. _Front. Neurosci._ 12, 891 (2018). Article  PubMed  PubMed Central  Google Scholar  * Shastri, B. J. et al. Photonics for artificial

intelligence and neuromorphic computing. _Nat. Photon._ 15, 102–114 (2021). Article  ADS  CAS  Google Scholar  * Song, S. et al. Recent progress of optoelectronic and all-optical

neuromorphic devices: A comprehensive review of device structures, materials, and applications. _Adv. Intell. Syst._ 3, 2000119 (2021). Article  Google Scholar  * Feldmann, J. et al.

Parallel convolutional processing using an integrated photonic tensor core. _Nature_ 589, 52–58 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Miller, D. A. Attojoule optoelectronics

for low-energy information processing and communications. _J. Lightwave Technol._ 35, 346–396 (2017). Article  ADS  CAS  Google Scholar  * Spall, J., Guo, X. & Lvovsky, A. I. Hybrid

training of optical neural networks. _Optica_ 9, 803–811 (2022). Article  ADS  Google Scholar  * Shen, Y. et al. Deep learning with coherent nanophotonic circuits. _Nat. Photon._ 11, 441–446

(2017). Article  ADS  CAS  Google Scholar  * Xu, S. et al. Optical coherent dot-product chip for sophisticated deep learning regression. _Light Sci. Appl._ 10, 221 (2021). Article  ADS  CAS

  PubMed  PubMed Central  Google Scholar  * Tait, A. N. et al. Neuromorphic photonic networks using silicon photonic weight banks. _Sci. Rep._ 7, 1–10 (2017). Article  CAS  Google Scholar  *

Zhou, W. et al. In-memory photonic dot-product engine with electrically programmable weight banks. _Nat. Commun._ 14, 2887 (2023). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar

  * Meng, X. et al. Compact optical convolution processing unit based on multimode interference. _Nat. Commun._ 14, 3000 (2023). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  *

Giamougiannis, G. et al. Analog nanophotonic computing going practical: silicon photonic deep learning engines for tiled optical matrix multiplication with dynamic precision. _Nanophotonics_

12, 963–973 (2023). Article  CAS  Google Scholar  * Giamougiannis, G. et al. Neuromorphic silicon photonics with 50 GHz tiled matrix multiplication for deep-learning applications. _Adv.

Photon._ 5, 016004–016004 (2023). Article  ADS  CAS  Google Scholar  * Pappas, C. et al. A 160 TOPS multi-dimensional AWGR-based accelerator for deep learning. In _Optical Fiber

Communication Conference_, pp. 4-3 (2024). * Pappas, C. et al. A TeraFLOP photonic matrix multiplier using time-space-wavelength multiplexed AWGR-based architectures. In _2024 Optical Fiber

Communications Conference and Exhibition (OFC)_, pp. 1–3 (2024). * De Marinis, L. et al. A codesigned integrated photonic electronic neuron. _IEEE J. Quantum Electron._ 58, 1–10 (2022).

Article  Google Scholar  * Sludds, A. et al. Delocalized photonic deep learning on the internet’s edge. _Science_ 378, 270–276 (2022). Article  ADS  CAS  PubMed  Google Scholar  * De

Marinis, L., Andriolli, N. & Contestabile, G. Analysis of integration technologies for high-speed analog neuromorphic photonics. _IEEE J. Quantum Electron._

https://doi.org/10.1109/JSTQE.2023.3273784 (2023). * Xu, X. et al. 11 TOPS photonic convolutional accelerator for optical neural networks. _Nature_ 589, 44–51 (2021). Article  ADS  CAS 

PubMed  Google Scholar  * Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. _Nature_ 562, 101–104 (2018). Article  ADS  CAS  PubMed 

Google Scholar  * Xu, M. et al. Dual-polarization thin-film lithium niobate in-phase quadrature modulators for terabit-per-second transmission. _Optica_ 9, 61–62 (2022). Article  ADS  CAS 

Google Scholar  * Lin, Z. et al. High-performance polarization management devices based on thin-film lithium niobate. _Light Sci. Appl._ 11, 93 (2022). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Billah, M. R. et al. Hybrid integration of silicon photonics circuits and InP lasers by photonic wire bonding. _Optica_ 5, 876–883 (2018). Article  ADS  CAS 

Google Scholar  * Wang, S. et al. High-performance integrated laser based on thin-film lithium niobate photonics for coherent ranging. _Laser Photon. Rev._ 2400224

https://doi.org/10.1002/lpor.202400224 (2024). * Chen, G. et al. High performance thin-film lithium niobate modulator on a silicon substrate using periodic capacitively loaded traveling-wave

electrode. _APL Photonics_ 7, 026103 (2022). Article  ADS  CAS  Google Scholar  * Kharel, P., Reimer, C., Luke, K., He, L. & Zhang, M. Breaking voltage–bandwidth limits in integrated

lithium niobate modulators using micro-structured electrodes. _Optica_ 8, 357–363 (2021). Article  ADS  Google Scholar  * Gokmen, T., Rasch, M.J. & Haensch, W. The marriage of training

and inference for scaled deep learning analog hardware. In _2019 IEEE International Electron Devices Meeting (IEDM)_, pp. 22-3 (2019). * Jansson, Y. & Lindeberg, T. Scale-invariant

scale-channel networks: Deep networks that generalise to previously unseen scales. _J. Math. Imaging Vis._ 64, 506–536 (2022). Article  MathSciNet  Google Scholar  * Pinkus, A. Approximation

theory of the MLP model in neural networks. _Acta Numerica_ 8, 143–195 (1999). Article  ADS  MathSciNet  Google Scholar  * Khotanzad, A. & Lu, J.-H. Classification of invariant image

representations using a neural network. _IEEE Trans. Acoust. Speech Signal Process._ 38, 1028–1038 (1990). Article  Google Scholar  * Amari, S.-i Backpropagation and stochastic gradient

descent method. _Neurocomputing_ 5, 185–196 (1993). Article  Google Scholar  * Dalal, K.R. Analysing the role of supervised and unsupervised machine learning in IoT. In _2020 International

Conference on Electronics and Sustainable Communication Systems (ICESC)_, pp. 75–79 (2020). * Lin, Z. et al. High-performance, intelligent, on-chip speckle spectrometer using 2D silicon

photonic disordered microring lattice. _Optica_ 10, 497–504 (2023). Article  ADS  CAS  Google Scholar  * Lever, J., Krzywinski, M. & Altman, N. Points of significance: Principal

component analysis. _Nat. Methods_ 14, 641–643 (2017). Article  CAS  Google Scholar  * Journée, M., Nesterov, Y., Richtárik, P., Sepulchre, R. Generalized power method for sparse principal

component analysis. _J. Mach. Learn. Res._ 11, 517–553 (2010). * Chang, W. & Zhang, M. Silicon-based multimode waveguide crossings. _J. Phys. Photon._ 2, 022002 (2020). Article  CAS 

Google Scholar  * Jaklin, M., García-Lesta, D., Lopez, P. & Brea, V.M. Global shutter CMOS vision sensors and event cameras for on-chip dynamic information. _Int. J. Circuit Theory

Appl._ 52, 3052–3065 (2024). * Dehkordi, M. A., Dousti, M., Mirsanei, S. M. & Zohoori, S. A dynamic power-efficient 4 GS/s CMOS comparator. _AEU Int. J. Electron. Commun._ 170, 154812

(2023). Article  Google Scholar  * Zou, J. et al. High resolution and ultra-compact on-chip spectrometer using bidirectional edge-input arrayed waveguide grating. _J. Light Technol._ 38,

4447–4453 (2020). Article  ADS  Google Scholar  * Mardoyan, H.et al. First 260-GBd single-carrier coherent transmission over 100 km distance based on novel arbitrary waveform generator and

thin-film lithium niobate I/Q modulator. In _European Conference and Exhibition on Optical Communication_, pp. 3-2 (2022). * Lin, X. et al. All-optical machine learning using diffractive

deep neural networks. _Science_ 361, 1004–1008 (2018). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Lindenmann, N. et al. Photonic wire bonding: a novel concept for chip-scale

interconnects. _Opt. Express_ 20, 17667–17677 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Mwase, C., Jin, Y., Westerlund, T., Tenhunen, H. & Zou, Z. Communication-efficient

distributed AI strategies for the IoT edge. _Future Gener. Comput. Syst._ 131, 292–308 (2022). * Beath, C., Becerra-Fernandez, I., Ross, J. & Short, J. Finding value in the information

explosion. MIT Sloan Manag. Rev. https://www.researchgate.net/publication/282560984_Finding_value_in_the_information_explosion (2012). * Rabah, K. Convergence of AI, IoT, big data and

blockchain: a review. _Lake Inst. J._ 1, 1–18 (2018). Google Scholar  Download references ACKNOWLEDGEMENTS X.C. acknowledges the Natural Science Foundation of China (Grant No. 62293523).

L.C. the SiEPICfab consortium, the B.C. Knowledge Development Fund (BCKDF), the Canada Foundation for Innovation (CFI), the Refined Manufacturing Acceleration Process (REMAP) network, the

Canada First Research Excellence Fund (CFREF), and the Quantum Materials and Future Technologies Program. Z.L. acknowledges the National Natural Science Funds of China (Grant No. 62405382).

The authors thank Simon Levasseur and Nathalie Bacon from the University of Laval for their technical support. The authors thank Xin Xin for his help in the experiment setup. We thank

Zhongguan Lin for his help in designing the electrical control circuits. The authors thank Xiaogang Qiang for his suggestion for Fig. 1. Part of the images shown in Fig. 1 were designed by

Freepik. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Electrical and Computer Engineering, The University of British Columbia, Vancouver, British Columbia, Canada Zhongjin

Lin, Shangxuan Yu, Jingxiang Song, Wangning Cai, Mustafa Hammood, Tianye Wang, Mohammed Al-Qadasi, Omid Esmaeeli, Matthew Mitchell, Nicolas A. F. Jaeger, Sudip Shekhar & Lukas

Chrostowski * State Key Laboratory of Optoelectronic Materials and Technologies, School of Electronics and Information Technology, Sun Yat-sen University, Guangzhou, Guangdong, China

Zhongjin Lin, Yuntao Zhu, Yanmei Lin, Wei Ke, Mengyue Xu, Siyuan Yu & Xinlun Cai * Department of Physics, Engineering Physics and Astronomy, Queen’s University, Kingston, Ontario, Canada

Bhavin J. Shastri & Hugh Morison * Department of Electrical and Computer Engineering, Université Laval, Québec City, Québec, Canada Arman Safarnejadian, Zibo Zheng, Leslie A. Rusch 

& Wei Shi * Advanced Electronics and Photonics Research Centre, National Research Council, Ottawa, Ontario, Canada Mohamed Rahim, Grzegorz Pakulski, Jens Schmid, Pedro Barrios & 

Weihong Jiang * Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, China Xun Guan Authors * Zhongjin Lin View author publications You can also search for this

author inPubMed Google Scholar * Bhavin J. Shastri View author publications You can also search for this author inPubMed Google Scholar * Shangxuan Yu View author publications You can also

search for this author inPubMed Google Scholar * Jingxiang Song View author publications You can also search for this author inPubMed Google Scholar * Yuntao Zhu View author publications You

can also search for this author inPubMed Google Scholar * Arman Safarnejadian View author publications You can also search for this author inPubMed Google Scholar * Wangning Cai View author

publications You can also search for this author inPubMed Google Scholar * Yanmei Lin View author publications You can also search for this author inPubMed Google Scholar * Wei Ke View

author publications You can also search for this author inPubMed Google Scholar * Mustafa Hammood View author publications You can also search for this author inPubMed Google Scholar *

Tianye Wang View author publications You can also search for this author inPubMed Google Scholar * Mengyue Xu View author publications You can also search for this author inPubMed Google

Scholar * Zibo Zheng View author publications You can also search for this author inPubMed Google Scholar * Mohammed Al-Qadasi View author publications You can also search for this author

inPubMed Google Scholar * Omid Esmaeeli View author publications You can also search for this author inPubMed Google Scholar * Mohamed Rahim View author publications You can also search for

this author inPubMed Google Scholar * Grzegorz Pakulski View author publications You can also search for this author inPubMed Google Scholar * Jens Schmid View author publications You can

also search for this author inPubMed Google Scholar * Pedro Barrios View author publications You can also search for this author inPubMed Google Scholar * Weihong Jiang View author

publications You can also search for this author inPubMed Google Scholar * Hugh Morison View author publications You can also search for this author inPubMed Google Scholar * Matthew

Mitchell View author publications You can also search for this author inPubMed Google Scholar * Xun Guan View author publications You can also search for this author inPubMed Google Scholar

* Nicolas A. F. Jaeger View author publications You can also search for this author inPubMed Google Scholar * Leslie A. Rusch View author publications You can also search for this author

inPubMed Google Scholar * Sudip Shekhar View author publications You can also search for this author inPubMed Google Scholar * Wei Shi View author publications You can also search for this

author inPubMed Google Scholar * Siyuan Yu View author publications You can also search for this author inPubMed Google Scholar * Xinlun Cai View author publications You can also search for

this author inPubMed Google Scholar * Lukas Chrostowski View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Z.L., X.C., and L.C. jointly

conceived the idea. Z.L. designed the device with help from Y.L., M.X., and T.W. M.R., G.P., J.S., P.B., and W.J. designed and fabricated DFB-buried heterostructure lasers with spot-size

converters. Y.Z. and W.K. fabricated the photonic chip. Z.L., S.X.Y., M.M., and J.S. performed the photonic wire bonding experiment. Z.L. assembled the entire device. Z.L. performed the

experiments with help from J.S., A.S., M.H., Z.Z., O.E., M.A.Q., and X.G. W.S., L.A.R., W.C., H.M., S.S., B.S., X.Q., N.J., and S.Y.Y. assisted with the theory and algorithm. Z.L., X.C.,

B.S., and L.C. supervised and coordinated the work. Z.L. and X.C., with help from B.S., wrote the manuscript with contributions from all co-authors. CORRESPONDING AUTHORS Correspondence to

Xinlun Cai or Lukas Chrostowski. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Leong

Chuan Kwek and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lin, Z., Shastri,

B.J., Yu, S. _et al._ 120 GOPS Photonic tensor core in thin-film lithium niobate for inference and in situ training. _Nat Commun_ 15, 9081 (2024). https://doi.org/10.1038/s41467-024-53261-x

Download citation * Received: 27 November 2023 * Accepted: 07 October 2024 * Published: 21 October 2024 * DOI: https://doi.org/10.1038/s41467-024-53261-x SHARE THIS ARTICLE Anyone you share

the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative