Point singularity array with metasurfaces

ABSTRACT Phase singularities are loci of darkness surrounded by monochromatic light in a scalar field, with applications in optical trapping, super-resolution imaging, and structured

light-matter interactions. Although 1D singular structures, like optical vortices, are common due to their robust topological properties, uncommon 0D (point) and 2D (sheet) singularities can

be generated by wavefront-shaping devices like metasurfaces. With the design flexibility of metasurfaces, we deterministically position ten identical point singularities using a single

illumination source. The phasefront is inverse-designed using phase-gradient maximization with an automatically-differentiable propagator and produces tight longitudinal intensity

confinement. The array is experimentally realized with a TiO2 metasurface. One possible application is blue-detuned neutral atom trap arrays, for which this field would enforce 3D

confinement and a potential depth around 0.22 mK per watt of incident laser power. We show that metasurface-enabled point singularity engineering may significantly simplify and miniaturize

the optical architecture for super-resolution microscopes and dark traps. SIMILAR CONTENT BEING VIEWED BY OTHERS ENGINEERING PHASE AND POLARIZATION SINGULARITY SHEETS Article Open access 07

July 2021 SINGULAR DIELECTRIC NANOLASER WITH ATOMIC-SCALE FIELD LOCALIZATION Article 17 July 2024 THREE-DIMENSIONAL OPTICAL TRAPPING WITH A LOW-NA OBJECTIVE USING A FLAT-TOP BEAM Article

Open access 16 May 2025 INTRODUCTION Optical singularities occur when some parameter of the electric field is undefined; for instance, phase singularities occur when the wavefront phase is

undefined at field zeros, and polarization singularities occur when at least one parameter of the polarization ellipse is undefined1. For random monochromatic scalar fields in a 3D space,

such as in speckle patterns, 1D linear singularities (lines or curves) are ubiquitous since they are robust against field perturbations. On the other hand, 0D (point) and 2D (sheet)

singularities are far less common as they do not share the same robustness. They tend to fragment into stable 1D linear singularities upon field perturbation2, such as stray light either

originating from external sources or deviations from the desired geometrical parameters of optical devices. Nevertheless, 2D singularities (membranes of darkness in 3D space) have been

engineered and experimentally realized using wavefront shaping devices like metasurfaces3. Such devices can be obtained by inverse design optimization so that the light field achieves a

large spatial gradient of the phase normal to the surface comprising the singularity. While it is straightforward to position bright spots of light using conventional computer generated

holography techniques such as Gerchberg-Saxton phase retrieval4,5, these methods perform poorly at structuring dark regions of subwavelength dimensions3. 0D point singularities require the

scalar field to vanish at only one point. These cold spots have been identified in the near-field of nanoparticles6 and individual spots may be controllably displaced by superposing plane

waves7. Lattices of points with vanishing intensity in a vector polarization field have also been generated in the transverse plane8,9. Here, we seek a method for deterministically placing

multiple 0D singularities that is not bound to periodic spacing and does not mandate the use of multiple beams. We present a straightforward method of deterministically positioning point

singularities in a cylindrically-symmetric field. This strategy produces singularities with tight confinement, i.e., small characteristic spatial dimensions with a rapid increase of the

field intensity (amplitude modulus squared) away from the singularity point. We begin by describing the physical intuition behind the phase gradient maximization technique based on the

geometrical structure of the 0D singularity. While the singularities are engineered for a scalar field corresponding to a fixed linear polarization, we also examine the full 3D polarization

distribution that would be generated by a realistic wavefront shaping device like a metasurface. We then experimentally realize a linear array of ten tightly confined point singularities in

the axial direction with a metasurface comprising TiO2 nanopillars on glass. As a potential application, we evaluate the suitability of the resultant singular fields for neutral atom

trapping in the blue-detuned regime, in which atoms are trapped in positions of darkness. While the engineered singularity array is very sensitive to the tilt of incident illumination, it is

robust to wavelength changes of the trapping laser and demonstrates 3D confinement with no escape channels. Metasurface-enabled traps have the potential to greatly simplify the optical

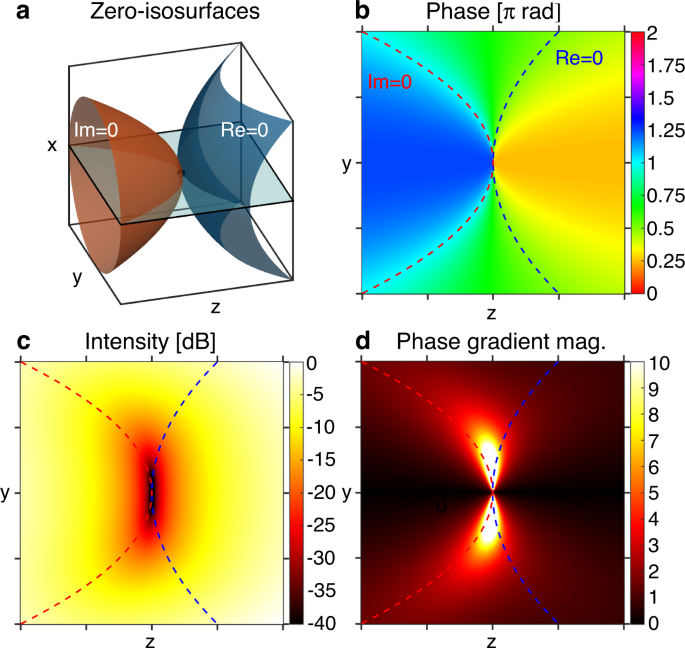
architecture required to produce dark optical traps for atoms or larger particles. RESULTS GEOMETRY AND TOPOLOGY OF 0D SINGULARITIES Point, i.e., 0D, phase singularities occur when a complex

scalar field _E_ is zero at only one point. That is, the real and imaginary zero-isosurfaces of _E_, loci of points for which Re(_E_) = 0 and Im(_E_) = 0, respectively, touch tangentially

at only one point (Fig. 1a). The field phase is defined for every point around the singularity except for the point itself (Fig. 1b) and the intensity decreases quadratically to zero towards

the singular point (Fig. 1c). Similar to 2D sheet-like singularities, 0D point singularities are uncommon and fragile. This is because they lack a property known as topological protection

and hence occur rarely in nature3,10. Nevertheless, they can be engineered to closely approximate 0D singularity behavior to within measurement uncertainties. Topological protection refers

to the robustness of a system against perturbations or defects, provided certain topological characteristics are preserved. For example, symmetry-protected bound states in the continuum

(BICs) are robust and continue to exist under small changes in system parameters, because of conserved and quantized topological charges that can only change under large system parameter

deviations11. In singular optics, topological protection refers to the persistent existence of the singularity under small changes in the surrounding medium or wave properties. They are

referred to as elementary optical singularities and include, for instance, the canonical orbital-angular-momentum (OAM) singularity in a scalar field or bright C-points in polarization

fields12. Upon perturbation, such elementary optical singularities are merely displaced and can only be annihilated by a large perturbation that merges two singularities of opposite charge.

Singularities that are not topologically protected, such as higher-order OAM modes, do not have this guarantee; they are destroyed or split into multiple topologically-protected

singularities under field perturbation. This is also observed in BICs when symmetry-breaking operations cause a V-point to fragment into topologically-protected C-points13. This fragility to

perturbation renders such singularities uncommon in nature10. ENGINEERING SINGULARITY CONFINEMENT As with singularities of other geometries, the 0D singularity is accompanied by a region of

large phase gradient magnitude |∇_ϕ_|2 = (∂_x__ϕ_)2 + (∂_y__ϕ_)2 + (∂_z__ϕ_)2 (Fig. 1d) which diverges to infinity at the position of the singularity. In optical fields, this phase

accumulation rate can be much larger than the field wavenumber _k_ = 2π/λ, indicating superoscillatory behavior14. While phase singularities can be engineered by enforcing perfect

destructive interference at a point, the confinement of the dark point is another critical parameter, especially in superresolution microscopy (e.g., STED15) and optical trapping. In these

applications, dark positions should ideally be fully surrounded by light (i.e., 3D confinement) with sharp field gradients (i.e., tightly confined/localized). These additional constraints on

the field distribution in the vicinity of a dark point cannot be satisfied by simply minimizing the field intensity at the target position of the 0D singularity. Here, we show that phase

gradient maximization can enforce singular behavior at a point while simultaneously achieving tight confinement around the singularity. To build intuition for this technique, we first

consider a complex field _E_ along a line, and compare the fields that are produced by a simple intensity minimization at _z_ = _0_ and a phase gradient maximization at that same point (Fig.

 2). To avoid plotting unrealistically high phase gradients, we show fields that have a finite minimum intensity ϵ>0. Such a system may not yield zero intensity due to fabrication

imperfections or optimization constraints. Optimization constraints arise when one seeks to balance multiple competing desired behaviors, e.g., in a multi-objective optimization for which

one simultaneously optimizes the field structure at different locations. Close to an intensity minimum, the real and imaginary field components (_E__r_ and _E__i_, respectively) are

approximately linear (Fig. 2a). Since engineering the singularity by minimizing the field intensity at _z_ = _0_ just enforces a small ϵ there, it is insensitive to the slopes of _E__r_ and

_E__i_ across the singularity, which can be shallow and thus produce a slowly varying field intensity minimum with weak localization. At _z_ = _0_, _E__r_ and _E__i_ change sign and thereby

produce a π phase shift across the field minimum. This shift in phase can be captured by the variation in phase gradient ∂_z__ϕ_, which has a broad and short peak at _z_ = _0_ (Fig. 2c).

Engineering a singularity by simply minimizing the intensity at the desired field minimum position does not give one control over the confinement there. On the other hand, maximizing the

phase gradient at _z_ = _0_ simultaneously achieves singular behavior and improves confinement. Intuitively, noting that the phase gradient can be written in terms of field gradients

∇_ϕ_=Im(∇_E_/_E_), maximizing ∇_ϕ_ not only minimizes the value of _E_ in the denominator but also maximizes the field gradients ∇_E_ in the numerator. This means that the slopes of _E__r_

and _E__i_ are steeper across the singularity, producing a more rapidly varying field intensity minimum with narrower spatial confinement (Fig. 2b). A higher peak phase gradient also yields

a taller and narrower phase gradient peak across the field minimum so that the accumulated phase across the minimum remains π (Fig. 2d). In three dimensions, 0D singularities are

characterized by large phase gradients in all directions. One has to simultaneously maximize the phase gradients at the same point to squeeze the singularity into a point, a task which poses

convergence difficulties since changing one directional gradient at a point inevitably affects the other gradients in the other directions. This problem is circumvented when the field is

constructed to be azimuthally (cylindrically) symmetric about the optical axis: i.e., the electric field E(_r,z_) is only a function of the radial distance from the optical axis _r_ and

longitudinal position along the optical axis _z_. One can produce 0D point singularities along the optical axis just by maximizing one directional gradient at each of the desired points: the

_z_-directed phase gradient. This exploitation of a system symmetry improves numerical convergence to an optimal design. OPTIMIZATION APPROACH FOR METASURFACE REALIZATION As a

proof-of-concept for 0D singularity engineering, we designed an array of ten 0D singularities spaced 3 µm apart (Fig. 3a) to be generated by a phase-only metasurface measuring 1 mm in

diameter, and illuminated by a narrowband laser centered at λ = 760 nm. Although we demonstrate a uniform array of singularities here, the algorithm can be applied to aperiodic singularity

patterns as well, and we show one such design in Supplementary Figure 1. Such a light field, structured longitudinally along the optical axis, is challenging to generate using conventional

holography methods that excel at designing only transverse field patterns. Full 3D holographic pattern generation with both transverse and longitudinal control remains an area of active

research16. We partition the cylindrically symmetric metasurface plane into 1001 annular regions, each 500 nm thick. Each annular region is assigned a transmission phase delay so that the

metasurface system can be parametrized by the 1001 phase delay values which serve as tunable optimization parameters. The phase profile from the metasurface is propagated into free space

(_z_ > 0) using a vectorial propagator17 built on an automatically differentiable platform (Tensorflow18), assuming that the incident field is linearly _x_-polarized for simplicity. The

process is generalizable to optimizing both transverse polarization components over the surface and is not restricted to single scalar fields. This automatically differentiable propagator

affords computationally efficient calculation of the exact numerical gradients of arbitrary objective functionals on the diffracted field. There are two steps in the optimization process. In

the first stage of optimization, we maximize the longitudinal phase gradient of the _x_-polarized _E__x_ field at ten equally-spaced target singularity positions from _z_ = 500 µm to _z_ = 

527 µm along the optical axis. The radially oriented phase gradient is identically zero due to azimuthal symmetry and continuity conditions for analytic fields: a nonzero radial phase

gradient along the optical axis will produce a kink in the phase gradient across the optical axis. This first step produces a 0D singularity at each of the target positions. The intensity

(i.e., |_E__x_ | 2 + |_E__y_ | 2 + |_E__z_ | 2) and _E__x_ phase profiles around each of the singular positions after this first step are plotted in Supplementary Figures 2 and 3,

respectively. In several positions, the real and imaginary zero-isolines come close but do not touch, indicating that these situations are close approximations of 0D singularities and not

mathematical 0D singularities. In the second stage of optimization, we use the optimized first stage result to equalize the phase gradient and second spatial derivative of |_E__x_ | 2 (as a

proxy for the intensity) over all the singularity positions and thus obtain nearly identical singularities across the array. The field intensity and phase profiles around each dark position

are plotted in Supplementary Figs. 4–5, respectively. The phase gradient profile of the _E__x_ field along the optical axis is plotted in Fig. 3b and shows identical large superoscillatory

values of 100_k__0_ at the singularity positions, as designed. High spatial resolution plots of the phase gradients around each singularity position are shown in Supplementary Fig. 6, which

also show that the full-width-at-half-maximum of the phase gradient magnitude is 2.3 nm for each singularity. The tight feature localization of optical singularities has been exploited for

precision displacement sensing19. The complex electric field components _E__x,y,z_ on the transverse plane under _x-_polarized illumination at the metasurface plane at each singularity

position are plotted in Supplementary Fig. 7 and the spatially-varying transverse polarization states (parametrized by the polarization ellipse distribution) are plotted in Supplementary

Fig. 8. The cross-polarized electric fields _E__y,z_ are generated from the vectorial propagation of the _x_-polarized field after the metasurface plane. _E__y,z_ vanishes on-axis due to

cylindrical symmetry and the fields close to the optical axis are predominantly _x_-polarized. An isolated zero field intensity position in a linearly polarized field is known as a V-point

polarization singularity20,21, thus if the metasurface is illuminated with linear polarized light, it produces an array of V-points. The inverse-designed phase profile along the metasurface

is unwrapped and plotted in Fig. 3c to show the long-range structure. Full details of the optimization process are in Supplementary Information section 1. The azimuthal symmetry of the

wavefront-shaping metasurface results in negligible OAM about the optical axis. Although singular optics and OAM are frequently discussed in the same context, they are distinct concepts in

complex beams comprising superpositions of many OAM eigenmodes22. The transverse OAM density about the optical axis and transverse components of the Poynting vector for each of the 0D

singularities (under _x_-polarized illumination) is plotted in Supplementary Fig. 9, which demonstrate negligible OAM and no energy circulation about the optical axis. Although optical

singularities are also located close to large intensity gradients, maximizing the _z_-directed intensity gradient instead of the phase gradient as a proxy for producing such singularities

does not afford precise control over the position of minimum intensity. The resultant positions of minimum intensity also do not have phase gradients appreciably larger than the vacuum

wavenumber. Supplementary Information section 2 discusses the result of optimizing the intensity gradients for a system of the same geometry and the resultant field profiles are plotted in

Supplementary Fig. 10. We fabricated a 1 mm diameter metasurface comprising 700 nm tall cylindrical TiO2 pillars on a fused silica substrate to enforce the required phase profile and

generate the ten 0D singularities. The fabrication process is similar to previously published work23 and involves electron beam lithography of the required nanopillar profile into electron

beam resist, followed by atomic layer deposition of amorphous TiO2 into the developed resist voids. Over-deposited TiO2 is etched back using reactive ion etching to leave free-standing

nanopillars. An opaque aluminum aperture is positioned around the metasurface to reduce stray light. Details of the nanofabrication process are in the Methods section and the nanopillar

library optical performance is plotted in Supplementary Fig. 11. At each metasurface position, we pick the nanopillar from the library that has the closest transmitted phase to the required

phase at that radial position. The non-uniform transmission amplitude of the meta-atom library introduces slight field deviations from the design field distribution, and we plot the

predicted field intensity and phase profiles incorporating these imperfections in Supplementary Figs. 12, 13, respectively. The field intensity structure is largely preserved but the phase

profile is slightly distorted near the intended singularity positions. This deviation arises because the 0D singularities are not topologically protected and were constructed by

finely-tuning the metasurface phase profile under the assumption of ideal uniform transmission. Non-idealities arising from a realistic nanopillar library thus slightly distort the dark

regions so that these positions are not mathematical singularities. While this deviation is likely not significant enough to impact applications which are sensitive to intensity profiles,

closer field behavior to the mathematical ideal can be obtained by including nonuniform transmission intensity of the nanopillar library during optimization24. Scanning electron microscope

images of the fabricated metasurface are shown in Fig. 3d. For characterization, the metasurface is illuminated with a narrowband distributed feedback diode laser (λ = 760.9 nm, 2 MHz

linewidth) coupled to a single mode fiber with collimated output, and the transmitted field through the metasurface is captured over 1201 longitudinal _z_-positions at steps of 50 nm, where

_z_ = 0 mm corresponds to the patterned surface of the metasurface, using a high magnification objective (×100, NA = 0.95) in a horizontal microscope system (Fig. 3e). The transmitted

intensity measurements are normalized to the incident power flux at the metasurface. Full experimental and data processing details are in Supplementary Information section 3. EXPERIMENTAL

LONGITUDINAL FIELD PROFILE The simulated cylindrically symmetric field intensity profile on the _xz_ plane in the vicinity of the ten 0D singularities is plotted in Fig. 4a. The experimental

intensity profiles in the longitudinal _xz_ and _yz_ planes are displayed in Fig. 4b, c, respectively, and demonstrate good agreement with the simulated profiles. The intensity profile

colormaps are adjusted to show the singularity region clearly and some parts of the surface plots are intentionally saturated to better show the singular regions. The unsaturated intensity

profiles are plotted in Supplementary Fig. 14. The maximum intensity value is indicated adjacent to each plot. The on-axis intensity comparison between the numerical and experimental cuts is

plotted in Fig. 4d. The longitudinal cuts were obtained by stacking the 1201 captures of the transverse field intensity. The captured transverse _xy_ field intensity at and between the ten

singular positions are shown in Fig. 4e, with rings of light around the dark singular points and bright on-axis spots in between singular positions. These transverse intensity pictures are

stacked in the longitudinal direction to produce the _xz_ and _yz_ cuts in Fig. 4b, c, respectively. The axial displacement of the experimental intensity profile with respect to the

simulated profile in the negative z-direction can be attributed to the incident laser wavelength of 760.9 nm being slightly longer than the design wavelength of 760 nm. We observe that the

experimental intensity is about a factor of four times smaller than the numerically predicted intensity. This is due to our intensity normalization choice and diffractive losses from the

breaking of the ideal periodic boundary condition that underlies our metasurface library. We underestimate the field intensity by measuring the transmitted field power profile after it

passes through the microscope objective and tube lens, thereby incorporating the reflective losses from multiple interfaces. We also overestimate the incident power by neglecting power loss

due to Fresnel reflections off the fused silica-air interface. EVALUATION OF ATOMIC TRAPPING POTENTIAL Due to their high intensity gradients, phase singularities are effective as optical

traps. Dielectric particles with a refractive index lower than the surrounding medium, reflective particles, and absorptive particles can all be trapped in the dark minimum of a beam, such

as that on the axis of a donut beam carrying orbital angular momentum25,26. For neutral atoms, depending on the sign of the detuning Δ _= ω-ω__0_ between the optical trap field frequency ω

and a strong atomic resonance frequency ω0, such atoms are attracted to either intensity maxima (red Δ < 0 detuning) or minima (blue Δ > 0 detuning)27. Most optical dipole traps for

neutral atoms are red traps which trap neutral atoms in arrays of tightly focused spots of light. Blue bottle traps with 3D spatial confinement, which trap the atoms in a dark spot

surrounded by light, are more difficult to realize but provide several key advantages over red traps. Atoms trapped in blue traps experience substantially lower scattering rates27 and

thereby longer coherence times28. Importantly, the trap laser can remain on during laser excitation with other coherent sources29. Techniques using a single structured beam have been able to

produce single blue traps28,30,31,32, more exotic bottle traps based on acoustic33,34 or ponderomotive35 forces, and arrays of blue traps in the transverse plane29,36. The state-of-the-art

blue trap array in active use is arguably the quantum gas microscope37, which holographically projects a two-dimensional optical lattice into a vacuum cell, thereby achieving thousands of

trap sites with individual optical access. A key challenge is ensuring that all traps have identical optical environments, including spatially-varying polarization states, as these would

shift the magnetic sublevels of the electronic states38. There is growing interest in using metasurfaces for the generation of atom traps39,40,41, where the multifunctional, compact

metasurface can replace multiple conventional optics and may even be located within the vacuum chamber. Recently, Hsu et al. performed single atom trapping with a red detuned trap generated

by a metalens inside the vacuum chamber41. The geometrical parameters of the 0D singularity array shown here are compatible with that of cold 87Rb Rydberg atom arrays42 (D2 line at 780.241 

nm) and may conceivably be deployed in the orthogonal geometry portrayed in Supplementary Fig. 15b, where a single metalens and single-sided illumination can generate the multiple blue traps

for optical interrogation in the transverse direction. This is in contrast to the in-line architecture of optical traps in which the trapping and optical interrogation is performed through

the same high numerical aperture objective. The trapping depth (in mK temperature units) per incident laser power is predicted to be 1.9 mK W−1 for the numerical simulation and 0.2 mK W−1

for the experimental intensity profile (Supplementary Information section 4). Both intensity profiles do not have any escape channels. Supplementary Information section 5 evaluates the

sensitivity of the structured optical field to changes in incident illumination tilt and incident wavelength on the metasurface (the longitudinal intensity profiles are visualized in

Supplementary Movie 1 and 2). Although the light field is tolerant to changes in the incident wavelength on the order of 10 nm, the effective angular bandwidth is around 2 mrad (0.11°). This

is similar to the field of view of 0.2° obtained in the previously reported metasurface red optical tweezer with NA = 0.5541. This limited angular bandwidth may be overcome with metasurface

angular dispersion engineering43 to obtain better angular performance by trading off unneeded chromatic bandwith44. Although the cross-polarized _E__y,z_ fields were not explicitly

controlled in the metasurface design process, the cross-sectional 3D polarization profile is highly similar across trap positions (Supplementary Fig. 7), producing similar optical

environments and hence equal magnetic sublevel shifts for trapped atoms. Passive metasurfaces excel in applications which afford very little volumetric and mass footprint while demanding

high performance under a narrow set of constraints. The latter is due to the inherent trade-off between chromatic control, angular dispersion, and efficiency44,45. Given the space

limitations in ultra-high-vacuum chambers and well-defined operational wavelengths for controlling and interrogating trapped particles in atomic physics, metasurfaces may be ideal for

compact, few-component atom trap architectures. The 0D singularities generated by such metasurfaces are suitable for deployment as blue-detuned trap arrays and can also be accentuated in

future work with dispersion engineering46 to perform additional functions under illumination with different laser wavelengths or capture fluorescent emissions from the trapped atoms. Beyond

optical traps, engineered 0D singularities may also be used in MINFLUX superresolution microscopy47 to capture information simultaneously from multiple points. METHODS COMPUTATIONAL DESIGN

OF METALENS The cylindrically symmetric phase-controlled metasurface at _z_ = 0 mm is parametrized by a set of 1001 annular rings, each of 500 nm radial extent, to produce a total lens with

a 500 µm radius. For each radial position, we assign a scalar _ϕ_ for the propagation phase delay of light there. This treats the metasurface as phase-only and cylindrically-symmetric. We

propagate this wavefront into the domain _z_ > 0 using the vectorial diffraction integral17 implemented on an automatically differentiable platform (Tensorflow18). For the first

optimization stage, at each singularity position, we compute the \(z\)-directed phase gradient of the field \(\partial \phi /\partial z\). The objective function \({F}_{1}\) to be minimized

is the negative minimum of the squares of the _z_-directed phase derivatives for each singularity position (Eq. 1). $${F}_{1}={-{{\min }}\left\{{\left(\frac{\partial {{{{{\rm{\phi

}}}}}}}{\partial {{{{{{\rm{z}}}}}}}_{{{{{{\rm{i}}}}}}}}\right)}^{2}\right\}}_{i=1,\ldots,{{{{{\rm{n}}}}}}}$$ (1) To improve convergence, we use a smooth approximation to the minimum

function, which is analytic instead of being piecewise continuous (Eq. 2). $${{\min }}\left({a}_{1},\ldots,\, {a}_{n}\right)=\frac{{{\log }}\left[{\sum }_{i}{{\exp }}\left(-s{\cdot

a}_{i}\right)\right]\,}{-s},\, s=\frac{100}{\frac{1}{n}{\sum }_{i}\left|{a}_{i}\right|} > 0$$ (2) In the second optimization stage, the objective function \({F}_{2}\) to be minimized is

the maximum of the deviations of the phase gradient to a large target phase gradient, set here to be 100 times the nominal field wavenumber \({k}_{0}\), plus penalty terms for differences in

the second spatial derivative of the on-axis intensity \(I\left(z\right)={\left|{E}_{x}(r=0,\, z)\right|}^{2}\) (Eq. 3). $${F}_{2}={{\max }}{\left(\frac{\partial \phi }{\partial

{z}_{i}}-100{k}_{0}\right)}_{i=1,\ldots,{{{{{\rm{n}}}}}}}^{2}+{c}_{1}\frac{\sigma {\left\{{\partial }_{z}^{2}I\left({z}_{i}\right)\right\}}_{i=1,\ldots,{{{{{\rm{n}}}}}}}}{\mu

{\left\{{\partial }_{z}^{2}I\left({z}_{i}\right)\right\}}_{i=1,\ldots,{{{{{\rm{n}}}}}}}}+{c}_{2}\frac{\sigma {\left\{{\partial

}_{r}^{2}I\left({z}_{i}\right)\right\}}_{i=1,\ldots,{{{{{\rm{n}}}}}}}}{\mu {\left\{{\partial }_{r}^{2}I\left({z}_{i}\right)\right\}}_{i=1,\ldots,{{{{{\rm{n}}}}}}}},$$ (3) where \(\sigma\)

refers to the population standard deviation and \(\mu\) is the population mean. \({c}_{1}\) and \({c}_{2}\) are weight parameters that are chosen so as to bring the three terms in

\({F}_{2}\) onto similar scales. We use a smooth approximation to the maximum function (Eq. 4) to improve convergence, which is analogous to the smooth approximation to the minimum function

described earlier. $${{\max }}\left({a}_{1},\ldots,{a}_{n}\right)=\frac{{{\log }}\left[{\sum }_{i}{{\exp }}\left(s{\cdot a}_{i}\right)\right]\,}{s},\,s=\frac{100}{\frac{1}{n}{\sum

}_{i}\left|{a}_{i}\right|} > 0,$$ (4) Full optimization details are contained in Supplementary Information section 1. NANOFABRICATION OF METALENS The metasurface comprises TiO2

nanopillars on a glass substrate (0.5-mm-thick JGS2-fused silica) and is fabricated using electron beam lithography, atomic layer deposition, and reactive ion etching processes23,48. The

nanopillar pattern is written into 700 nm thick ZEP520A electron-beam resist (Zeon Specialty Materials Inc.) using a high-speed 50 kV electron-beam lithography system (Elionix HS-50)

followed by development in chilled _o_-Xylene (puriss. p.a., ≥ 99.0% (GC), Sigma Aldrich). The patterned holes are then conformally filled with amorphous TiO2 through a low-temperature

atomic layer deposition process (Cambridge NanoTech Savannah) until the holes are completely filled. The over-deposited TiO2 is etched back using reactive ion etching with CHF3/Ar/O2 mixture

(Oxford PlasmaPro 100 Cobra ICP Etching System) until the resist layer is exposed. The residual resist is removed by a downstream plasma asher (Matrix Plasma Asher, Matrix Systems Inc.),

which leaves free-standing TiO2 nanopillars. A 1.1 mm diameter opaque aperture is formed around the 1 mm diameter metasurface by photolithography using S1818 photoresist (Kayaku Advanced

Materials Inc.), electron beam evaporation of 150 nm thick aluminum (Sharon electron beam evaporator), followed by a lift-off process via overnight immersion in Remover PG solution (Kayaku

Advanced Materials Inc.). EXPERIMENTAL CHARACTERIZATION OF SINGULARITY ARRAY A 760.9 nm single frequency distributed feedback (DFB) laser (TOPTICA Eagleyard GmbH) is driven with a constant

current source (Newport 505 Laser Diode Driver) and kept at a constant temperature (Newport 325 Thermoelectric Cooler Driver). The single mode fiber-coupled output is collimated with a

reflective collimator (Thorlabs RC12APC-P01) and is incident on the fused silica face of the metasurface. The metasurface _z_-position is controlled using a closed-loop piezo-motor stage

with nm resolution (Attocube ECSx3030). The transmitted light is captured using a horizontal microscope system comprising a high NA objective (Olympus 100x MPLAPON NA = 0.95), tube lens

(Thorlabs TTL-180A) and CMOS camera (Thorlabs DCC1545M). The intensity image is captured over a range of longitudinal _z_-positions at steps of 50 nm, where _z_ = 0 mm corresponds to the

patterned surface of the metasurface. At each _z_-position, the system is allowed to stabilize for 10 s before multiple intensity images are captured at different exposure times ranging from

0.05 ms to 163 ms. These multiple exposure images are later weighted by their respective exposure times and stacked to remove saturated pixels and produce a composite image with a large

intensity dynamic range. Further experimental details are contained in Supplementary Information section 3. REPORTING SUMMARY Further information on research design is available in the 

Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY The figure and supplementary data generated in this study have been deposited in the Figshare database under

accession code https://doi.org/10.6084/m9.figshare.2258052149. CODE AVAILABILITY The code that supports the findings of this study is available from the corresponding author upon request.

REFERENCES * Dennis, M. R., O’Holleran, K. & Padgett, M. J. In _Progress in Optics_ Vol. 53 (ed. Wolf, E.), 293–363 (Elsevier B.V., 2009). * Dennis, M. R. Rows of optical vortices from

elliptically perturbing a high-order beam. _Opt. Lett._ 31, 1325–1327 (2006). Article  ADS  PubMed  Google Scholar  * Lim, S. W. D., Park, J.-S., Meretska, M. L., Dorrah, A. H. &

Capasso, F. Engineering phase and polarization singularity sheets. _Nat. Commun._ 12, 4190 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Gerchberg, R. W. & Saxton,

W. Phase determination for image and diffraction plane pictures in the electron microscope. _Optik_ 34, 275–284 (1971). Google Scholar  * Gerchberg, R. W. & Saxton, W. O. A practical

algorithm for the determination of phase from image and diffraction plane pictures. _Optik_ 35, 237–246 (1972). Google Scholar  * Haggui, M. et al. Spatial confinement of electromagnetic hot

and cold spots in gold nanocubes. _ACS Nano_ 6, 1299–1307 (2012). Article  CAS  PubMed  Google Scholar  * Vernon, A. J. & Rodríguez-Fortuño, F. J. Creating and moving nanoantenna cold

spots anywhere. _Light Sci. Appl_ 11, 258 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Ruchi, Pal, S. K. & Senthilkumaran, P. Generation of V-point polarization

singularity lattices. _Opt. Express_ 25, 19326 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Desai, J., Gangwar, K. K., Ruchi, Khare, K. & Senthilkumaran, P. Generation of V-point

polarization singularity array by Dammann gratings. _Appl. Phys. B_ 128, 108 (2022). Article  ADS  CAS  Google Scholar  * Spaegele, C. M. et al. Topologically Protected Optical Polarization

Singularities in Four-Dimensional Space. _Sci. Adv._ In press, https://doi.org/10.1126/sciadv.adh0369 (2023). * Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological

nature of optical bound states in the continuum. _Phys. Rev. Lett._ 113, 257401 (2014). Article  ADS  PubMed  Google Scholar  * Liu, W., Liu, W., Shi, L. & Kivshar, Y. Topological

polarization singularities in metaphotonics. _Nanophotonics_ 10, 1469–1486 (2021). Article  CAS  Google Scholar  * Liu, W. et al. Circularly polarized states spawning from bound states in

the continuum. _Phys. Rev. Lett._ 123, 116104 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Berry, M. ed. In _A Half-Century of Physical Asymptotics and Other Diversions_ 483–493

(World Scientific, 2017). * Hell, S. W. & Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. _Opt.

Lett._ 19, 780–782 (1994). Article  ADS  CAS  PubMed  Google Scholar  * Zamboni-Rached, M., Ambrosio, L. A., Dorrah, A. H. & Mojahedi, M. Structuring light under different polarization

states within micrometer domains: exact analysis from the Maxwell equations. _Opt. Express_ 25, 10051 (2017). Article  PubMed  Google Scholar  * Marathay, A. S. & McCalmont, J. F. Vector

diffraction theory for electromagnetic waves. _J. Opt. Soc. Am. A_ 18, 2585–2593 (2001). Article  ADS  MathSciNet  CAS  Google Scholar  * Abadi, M. et al. TensorFlow: a system for

large-scale machine learning. In _Proc. 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’16_) (ed. Keeton, K. & Roscoe, T.) 265–283 (2016). * Yuan, G. H. &

Zheludev, N. I. Detecting nanometric displacements with optical ruler metrology. _Science_ 364, 771–775 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Freund, I. Polarization flowers.

_Opt. Commun._ 199, 47–63 (2001). Article  ADS  CAS  Google Scholar  * Freund, I. Polarization singularity indices in Gaussian laser beams. _Opt. Commun._ 201, 251–270 (2002). Article  ADS

  CAS  Google Scholar  * Berry, M. V. & Liu, W. No general relation between phase vortices and orbital angular momentum. _J. Phys. A Math. Theor._ 55, 374001 (2022). Article  MathSciNet

  MATH  Google Scholar  * Devlin, R. C., Khorasaninejad, M., Chen, W. T., Oh, J. & Capasso, F. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. _Proc. Natl

Acad. Sci. USA_ 113, 10473–10478 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Lim, S. W. D., Meretska, M. L. & Capasso, F. A high aspect ratio inverse-designed

Holey Metalens. _Nano Lett._ 21, 8642–8649 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Ashkin, A., Dziedzic, J. M., Bjorkholm, J. E. & Chu, S. Observation of a single-beam

gradient force optical trap for dielectric particles. _Opt. Lett._ 11, 288–290 (1986). Article  ADS  CAS  PubMed  Google Scholar  * He, H., Heckenberg, N. R. & Rubinsztein-Dunlop, H.

Optical particle trapping with higher-order doughnut beams produced using high efficiency computer generated holograms. _J. Mod. Opt._ 42, 217–223 (1995). Article  ADS  Google Scholar  *

Grimm, R., Weidemüller, M. & Ovchinnikov, Y. B. Optical dipole traps for neutral atoms. _Adv. At., Mol. Opt. Phys._ 42, 95–170 (2000). Article  ADS  CAS  Google Scholar  * Ozeri, R.,

Khaykovich, L. & Davidson, N. Long spin relaxation times in a single-beam blue-detuned optical trap. _Phys. Rev. A_ 59, 1750–1753 (1999). Article  ADS  Google Scholar  * Huft, P. et al.

Simple, passive design for large optical trap arrays for single atoms. _Phys. Rev. A_ 105, 063111 (2022). Article  ADS  CAS  Google Scholar  * Xu, P., He, X., Wang, J. & Zhan, M.

Trapping a single atom in a blue detuned optical bottle beam trap. _Opt. Lett._ 35, 2164–2166 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Yu, H. et al. Chip-scale molecule trapping

by a blue-detuned metasurface hollow beam. _J. Opt._ 22, 045104 (2020). Article  ADS  CAS  Google Scholar  * Ling, C., Yin, Y., Liu, Y., Li, L. & Xia, Y. Generation of a blue-detuned

optical storage ring by a metasurface and its application in optical trapping of cold molecules. _Chin. Phys. B_ 32, 023301 (2023). Article  ADS  Google Scholar  * Zhang, P. et al.

Generation of acoustic self-bending and bottle beams by phase engineering. _Nat. Commun._ 5, 4316 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Chen, D.-C., Zhu, X.-F., Wei, Q., Wu,

D.-J. & Liu, X.-J. Dynamic generation and modulation of acoustic bottle-beams by metasurfaces. _Sci. Rep._ 8, 12682 (2018). Article  ADS  PubMed  PubMed Central  Google Scholar  *

Barredo, D. et al. Three-dimensional trapping of individual rydberg atoms in ponderomotive bottle beam traps. _Phys. Rev. Lett._ 124, 023201 (2020). Article  ADS  CAS  PubMed  Google Scholar

  * Piotrowicz, M. J. et al. Two-dimensional lattice of blue-detuned atom traps using a projected Gaussian beam array. _Phys. Rev. A_ 88, 1–8 (2013). Article  Google Scholar  * Bakr, W. S.,

Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. _Nature_ 462, 74–77 (2009). Article  ADS  CAS

  PubMed  Google Scholar  * Garcia, S., Reichel, J. & Long, R. Improving the lifetime in optical microtraps by using elliptically polarized dipole light. _Phys. Rev. A_ 97, 023406

(2018). Article  ADS  CAS  Google Scholar  * Zhu, L. et al. A dielectric metasurface optical chip for the generation of cold atoms. _Sci. Adv._ 6, 4–9 (2020). Article  ADS  Google Scholar  *

Xiao, Y. et al. Efficient generation of optical bottle beams. _Nanophotonics_ 10, 2893–2901 (2021). Article  CAS  Google Scholar  * Hsu, T.-W. et al. Single-atom trapping in a

metasurface-lens optical tweezer. _PRX Quantum_ 3, 030316 (2022). Article  ADS  Google Scholar  * Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays.

_Science_ 354, 1024–1027 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Zhang, X. et al. Controlling angular dispersions in optical metasurfaces. _Light Sci. Appl_ 9, 34–37 (2020).

Article  CAS  Google Scholar  * Shastri, K. & Monticone, F. Bandwidth bounds for wide-field-of-view dispersion-engineered achromatic metalenses. _EPJ Appl. Metamaterials_ 9, 16 (2022).

Article  ADS  Google Scholar  * Presutti, F. & Monticone, F. Focusing on bandwidth: achromatic metalens limits. _Optica_ 7, 624–631 (2020). Article  ADS  CAS  Google Scholar  * Chen, W.

T., Zhu, A. Y. & Capasso, F. Flat optics with dispersion-engineered metasurfaces. _Nat. Rev. Mater._ 5, 604–620 (2020). Article  ADS  Google Scholar  * Balzarotti, F. et al. Nanometer

resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. _Science_ 355, 606–612 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Khorasaninejad, M. et al.

Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. _Science_ 352, 1190–1194 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Lim, S. W.

D. et al. Data for Point singularity array with metasurfaces. _Figshare_ https://doi.org/10.6084/m9.figshare.22580521 (2023). Download references ACKNOWLEDGEMENTS S.W.D.L. is supported by

A*STAR Singapore through the National Science Scholarship Scheme. J.S.P. is on leave from the Korea Institute of Science and Technology. M.L.M. is supported by NWO Rubicon Grant

019.173EN.010, by the Dutch Funding Agency NWO. This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-22-1-0243 (F.C.). This

work was performed in part at the Harvard University Center for Nanoscale Systems (CNS); a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported

by the National Science Foundation under NSF award no. ECCS-2025158. The computations in this paper were run on the FASRC Cannon cluster supported by the FAS Division of Science Research

Computing Group at Harvard University. The authors thank Mikhail Lukin (Harvard University), Brandon Grinkemeyer (Harvard University), and Sooshin Kim (Harvard University) for helpful

discussions. AUTHOR INFORMATION Author notes * These authors contributed equally: Soon Wei Daniel Lim, Joon-Suh Park AUTHORS AND AFFILIATIONS * Harvard John A. Paulson School of Engineering

and Applied Sciences, 9 Oxford Street, Cambridge, MA, 02138, USA Soon Wei Daniel Lim, Joon-Suh Park, Dmitry Kazakov, Christina M. Spägele, Ahmed H. Dorrah, Maryna L. Meretska & Federico

Capasso * Nanophotonics Research Center, Korea Institute of Science and Technology, Seoul, 02792, Republic of Korea Joon-Suh Park Authors * Soon Wei Daniel Lim View author publications You

can also search for this author inPubMed Google Scholar * Joon-Suh Park View author publications You can also search for this author inPubMed Google Scholar * Dmitry Kazakov View author

publications You can also search for this author inPubMed Google Scholar * Christina M. Spägele View author publications You can also search for this author inPubMed Google Scholar * Ahmed

H. Dorrah View author publications You can also search for this author inPubMed Google Scholar * Maryna L. Meretska View author publications You can also search for this author inPubMed 

Google Scholar * Federico Capasso View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.W.D.L. conceived the algorithm and design with input

from A.H.D. J.S.P. fabricated the samples. S.W.D.L., J.S.P., and D.K. designed the experiment and characterized samples. C.M.S. derived the connections to trap confinement and perturbation

sensitivity. M.L.M. clarified applications of the system. S.W.D.L. wrote the manuscript with contributions from all authors. F.C. supervised the research. CORRESPONDING AUTHOR Correspondence

to Soon Wei Daniel Lim. ETHICS DECLARATIONS COMPETING INTERESTS S.W.D.L., J.S.P., A.H.D, M.L.M., and F.C. are the inventors on a relevant provisional patent application (application number:

US20230021549A1) owned by Harvard University. The authors declare no other competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewers

for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY

MOVIE 1 SUPPLEMENTARY MOVIE 2 REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lim, S.W.D., Park, JS., Kazakov, D. _et al._ Point singularity array with metasurfaces. _Nat Commun_ 14, 3237 (2023).

https://doi.org/10.1038/s41467-023-39072-6 Download citation * Received: 27 November 2022 * Accepted: 23 May 2023 * Published: 05 June 2023 * DOI: https://doi.org/10.1038/s41467-023-39072-6

SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to

clipboard Provided by the Springer Nature SharedIt content-sharing initiative