Filming movies of attosecond charge migration in single molecules with high harmonic spectroscopy

ABSTRACT Electron migration in molecules is the progenitor of chemical reactions and biological functions after light-matter interaction. Following this ultrafast dynamics, however, has been

an enduring endeavor. Here we demonstrate that, by using machine learning algorithm to analyze high-order harmonics generated by two-color laser pulses, we are able to retrieve the complex

amplitudes and phases of harmonics of single fixed-in-space molecules. These complex dipoles enable us to construct movies of laser-driven electron migration after tunnel ionization of N2

and CO2 molecules at time steps of 50 attoseconds. Moreover, the angular dependence of the migration dynamics is fully resolved. By examining the movies, we observe that electron holes do

not just migrate along the laser polarization direction, but may swirl around the atom centers. Our result establishes a general scheme for studying ultrafast electron dynamics in molecules,

paving a way for further advance in tracing and controlling photochemical reactions by femtosecond lasers. SIMILAR CONTENT BEING VIEWED BY OTHERS ATOMIC-SCALE IMAGING OF LASER-DRIVEN

ELECTRON DYNAMICS IN SOLIDS Article Open access 02 October 2024 EXTRACTING SUB-CYCLE ELECTRONIC AND NUCLEAR DYNAMICS FROM HIGH HARMONIC SPECTRA Article Open access 28 January 2021 TOWARDS

SIMULTANEOUS IMAGING OF ULTRAFAST NUCLEAR AND ELECTRONIC DYNAMICS IN SMALL MOLECULES Article Open access 18 March 2025 INTRODUCTION Understanding the ultrafast motion of electrons and nuclei

after light-molecule interaction is fundamental to a broad range of chemical reactions and biological processes1,2,3,4,5,6,7. With the advent of attosecond light pulses at the dawn of the

21st century8,9,10, various emerging techniques have been implemented by using attosecond pulse in combination with a femtosecond infrared (IR) pulse in a pump–probe configuration, such as

attosecond extreme-ultraviolet (XUV) transient absorption spectroscopy11,12, attosecond streaking technique13 and mass/ion spectroscopy14, making it possible to observe and partially

manipulate the electronic degrees of freedom in molecular systems. Quantum mechanically, after an electron was suddenly removed, the molecule is represented by a wave packet which is a

complex-valued many-particle wavefunction of all the electrons and the nuclei of the molecule. Since electrons move on much faster (attosecond) timescales than the heavier nuclei (few to

few-ten femtoseconds), within the first femtosecond, the nuclei positions can be assumed fixed and the electron wave packet (EWP) can be expressed as a superposition of the electronic

eigenstates, which will oscillate with the frequencies of the energy differences of the eigenstates. In previous publications by Cederbaum and coworkers1,2, such time dependence of the

electric charge density was called charge migration. This definition thus neglects the coupling from the escaping electron. On a longer timescale, the time-dependent EWP would cause the

change of electronic potential landscape, forcing the nuclear wave packet to evolve in time. Ultrafast electron diffraction can be used to extract time-dependent nuclear dynamics15,16,17,

from which molecular movie can be constructed to provide a visualization of the nuclear motion. An equivalent attosecond electron movie of charge migration, however, is not readily available

in conventional pump–probe experiments due to the limited time resolution by the pulse duration of the IR field18,19. Obtaining charge migration directly from experiment has been a

challenging topic with great interest in the past decade. In ref. 19, a pseudo pump–probe protocol based on the recollision mechanism20,21 of electrons in the laser field was discussed. In

this process, the electron dynamics is triggered at the ionization step (pump), and probed at the recollision instant by the returning electron, either through elastic scattering with

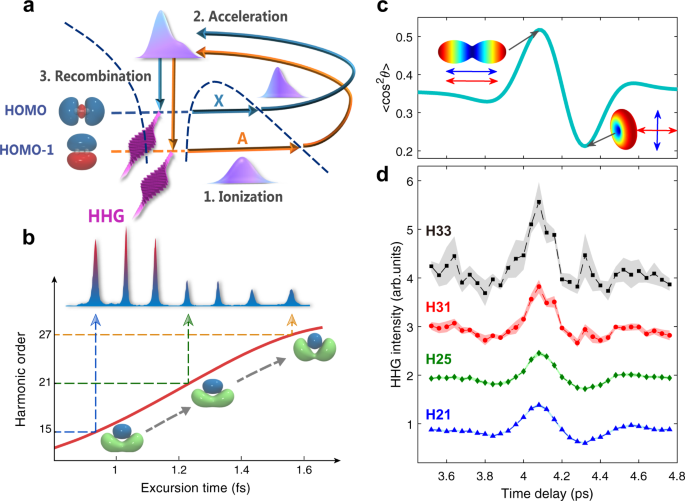
molecular ion or harmonic spectra by electron-ion recombination [see Fig. 1a]. Probing static or dynamic molecular structure using the diffraction image or high-order harmonic generation

(HHG) are called laser-induced electron diffraction (LIED)22,23,24,25 and high harmonic spectroscopy (HHS)26,27,28,29,30,31, respectively. In HHS, the temporal resolution arises from the

intrinsic frequency chirp of harmonic emission32, i.e., different harmonic orders are associated with well-defined ionization-recombination delays spent by the electron in the continuum [see

Fig. 1b], which can reach about 100 as for a commonly-used 800-nm laser field26,27,28. The spatial resolution of HHS comes from the de Broglie wavelength of the recombining electron and can

reach sub-ångström29,30,31. Recently, using HHS, charge migration of ionized iodoacetylene (HCCI) was first reported by Kraus et al.28. Note that for charge migration derived from HHS the

EWP evolves in the intense laser field while the original charge migration defined by Cederbaum et al.1,2 are electron dynamics under the field-free condition. In this article, we make

distinction by calling the electron dynamics in HHS laser-driven charge migration. As demonstrated in Ref. 28, to reconstruct electron dynamics from experimental harmonic spectra, one has to

address many challenges. First, reconstruction is an inverse scattering problem, which is generally solved by iterative methods. Reconstruction is possible only if the scattering theory is

on firm ground. Second, the laser-driven electron dynamics is a property of a single molecule at a fixed position, thus it depends on the alignment angle of the molecular axis with respect

to laser polarization. Since molecules cannot be aligned perfectly in experiment, the measured harmonics are the result of a coherent superposition of individual radiation weighted by the

angular distribution of the molecules33,34,35. By taking angular averaged harmonic spectra from the experimental data, the phases of harmonics are severely compromised (see Supplementary

Note 3), which would incur the loss of dynamics information of EWP that is at the heart of charge migration. Thus, it is critical to extract fixed-in-space single-molecule harmonic

amplitudes and phases. Such a deconvolution or similar ones should be carried out in all measurements involving gas-phase molecules if single-molecule parameters are to be extracted, which,

however, has not been properly treated in all of existing publications of HHS. In this work, this nontrivial deconvolution has been carried out. Besides, to extract charge migration, extra

parameters, i.e., the population coefficients of different cation states, that describe the EWP of a single molecule should be obtained as well. Thus, it is also necessary to evaluate if

adequate experimental data are available to ensure accurate retrieval of charge migration. Here we demonstrate that, by properly addressing the above three issues, we have succeeded in

filming movies of laser-driven charge migration in the molecular ion using HHS to reveal substantial sub-ångström electron migration. Since electron dynamics runs on the timescale of about

20 as (one atomic unit of time is 24 as), while the emission time difference between two odd harmonics by an 800-nm laser is about 100 as, we shorten this interval by half, by generating

both even and odd harmonics with a two-color laser field. With harmonic spectra from both single-color and two-color lasers in standard molecular alignment measurements, together with the

powerful modern machine learning (ML) algorithm, we have abundant data to retrieve the complex dipole amplitude and phase of each fixed-in-space molecule to construct the charge migration

movies. Thus, the alignment-angle-resolved molecular charge migration in the laser field has been fully characterized. RESULTS DECIPHERING CHARGE MIGRATION WITH HHS We first explain how

ultrafast charge migration is encoded in and how it can be identified from the molecular HHG signals. After strong-field tunneling ionization, the molecule in general is left in the ground

as well as several nearby electronically excited states of the ion1,2,3,4,36,37,38. Once the electron is ejected, the occupation amplitudes of these electronic states would change with time,

under the influence of the external laser field, creating a time-dependent many-electron wave packet, or equivalently, an electron–hole wave packet. The time dependence of the modulus

square of the wave packet is called electron charge (or hole) migration. Such hole dynamics is encoded in the harmonic spectra of each single molecule36,37,38. To decipher electron dynamics

from the harmonic spectra, we choose the two most widely studied molecules N2 and CO2 as the candidates to demonstrate our scheme. First, we consider N2. As illustrated in Fig. 1a, the two

channels (Channel _X_ and _A_) relevant to HHG in N2 are associated with the ground \({\tilde{X}}^{2}{{{\Sigma }}}_{{{{{{{{\rm{g}}}}}}}}}\) and first excited \({\tilde{A}}^{2}{{{\Pi

}}}_{{{{{{{{\rm{u}}}}}}}}}\) states of N\({}_{2}^{+}\) ion. In molecular orbital picture, these two channels correspond to ionization of an electron from the two highest-occupied molecular

orbitals, HOMO and HOMO-1, respectively. Owing to the different symmetries of these orbitals, HHG from different ionization channels depends differently on molecular alignment. Figure 1c

depicts the typical alignment distributions of N2 molecules near the half revival period, while Fig. 1d shows the typical harmonic spectra measured in the experiment (for experimental

details, see Methods and Supplementary Note 1). When molecules are aligned (anti-aligned) with respect to laser polarization, the signals of lower order harmonics (e.g., H21 and H25) are

strong (weak) because they are generated from the HOMO orbital. For higher orders, like H31 and H33, the signals receive a substantial contribution from the HOMO-1 orbital and thus becomes

quite large when the molecules are anti-aligned. These properties of the harmonic spectra of N2 have been well-studied experimentally39 and can be calculated with quantitative rescattering

(QRS) theory40,41,42,43. Similar results are also observed in HHG from CO2 molecule (see Supplementary Note 2). The different alignment dependence of the contribution to HHG from multiple

molecular orbitals allows us to access their complex population amplitudes in the complex wave packet of the molecular ion, from which ultrafast charge migration can be uncovered. RETRIEVAL

OF SINGLE-MOLECULE DIPOLE For a parallel configuration of the polarizations of the alignment and probe pulses, the time-dependent harmonic signal is given by33,34 $$S(\omega,\ \tau )={\left|

\int\nolimits_{0}^{\pi }D(\omega,\, \theta )\rho (\theta,\, \tau )\sin\theta {{{{{\rm{d}}}}}}\theta \right |}^{2},$$ (1) where _θ_ is the alignment angle of the molecule, _τ_ is the time

delay between these two pulses, _D_(_ω_, _θ_) is the fixed-angle-dependent total dipole moment from the single-molecule response, and _ρ_(_θ_, _τ_) is the angular distribution of molecules

at delay _τ_. In our experiment, _ρ_(_θ_, _τ_) is determined with method in Ref. 44. Note that perfect molecular alignment cannot be achieved in experiment. Our simulations show that

single-molecule harmonic amplitudes and phases deviate substantially from the angle-averaged ones (see Supplementary Note 3). To obtain molecular-frame electron dynamics, the first and

foremost step (omitted in all previous literature) is to decode angle-dependent single-molecule dipole moment _D_(_ω_, _θ_) (including both amplitude and phase) from the measured harmonic

signals. However, to solve this inverse problem directly is rather difficult since Eq. (1) is nonlinear and is ill-posed. Here, we introduce ML to this problem. The modern ML algorithm has

been demonstrated to have remarkable abilities in characterizing complex sets of data with a high degree of accuracy, and has been widely utilized in genetics45, condensed-matter physics46,

and material science47. We show here that it can effectively deal with the complicated decoding in HHS (see Methods and Supplementary Note 4). The second step of our reconstruction is to

disentangle the multichannel contributions from the total single-molecule dipole moment _D_(_ω_, _θ_) obtained in the first step. Driven by a one-color 800-nm probe pulse, only one set of

_D_(_ω_, _θ_) can be obtained for each harmonic order which is insufficient for the reconstruction. To overcome this problem, we employed an additional parallel two-color laser field to

generate harmonics. This two-color field consists of an intense 800-nm fundamental field and a weak second-harmonic (SH) field. The SH field is weak (~2 × 10−3 of the fundamental field),

which barely alters the electron dynamics of the molecular ion (see Supplementary Note 5), but could affect the intensities and phases of even harmonics as in ref. 48. Thus, measurement of

harmonics at different relative phases between the fundamental and SH fields can replenish the additional data set needed to retrieve multichannel contributions in the second step. Figure 

2a, b show the time-dependent signals of H22 and H27 from N2 measured as a function of the relative phase of the two-color laser fields. One can see that the modulation of HHG intensity

depends sensitively on the relative phase, and different harmonic orders present different dependences. Applying the ML-based reconstruction procedure to each harmonic order, we can obtain

the time-dependent complex mixing coefficients of the multiple orbitals of the molecular cation, for each fixed-in-space angle, at the excursion time when the recombination of that harmonic

order occurs, as illustrated in Fig. 1b. Figure 2c shows the reconstructed population amplitudes of the ground \(\tilde{X}\) state of the N\({}_{2}^{+}\) ion for four specific alignment

angles versus the excursion time. The circles indicate the data extracted from the experiment for harmonics from H15 to H27 (including even and odd orders). Figure 2d shows the reconstructed

relative phase between the wavefunctions of \(\tilde{X}\) and \(\tilde{A}\) states. With these parameters, a complex-valued time-dependent wave packet from the two holes \(\tilde{X}\) and

\(\tilde{A}\) can be constructed for N\({}_{2}^{+}\). We have also carried out the measurements for CO2 molecules. Harmonic spectra of CO2 involves three electronic states of the ion, the

ground \(\tilde{X}\) (HOMO), the first \(\tilde{A}\) (HOMO-1) and second \(\tilde{B}\) (HOMO-2) excited states36,37. Using the same procedure as for N2, the reconstructed populations and

relative phases of these three ion states are shown in Fig. 2e, f and g, h, respectively. With these parameters, a complex-valued time-dependent wave packet from the three holes

\(\tilde{X}\), \(\tilde{A}\) and \(\tilde{B}\) can be constructed for CO\({}_{2}^{+}\). To evaluate our reconstructions, we have carried out calculations based on the time-dependent density

functional theory (TDDFT) to simulate the parameters we obtained. The theoretical calculations are in reasonable agreement with the reconstructions (see Supplementary Note 5). FILMING

ATTOSECOND CHARGE MIGRATION IN THE LASER FIELD To visualize hole dynamics, we have calculated the modulus square of the wave packet versus time for N\({}_{2}^{+}\) and CO\({}_{2}^{+}\) with

the data in Fig. 2c–h. To quantify attosecond charge migration processes, we first examine hole dynamics of CO\({}_{2}^{+}\) when the fixed-in-space molecule is aligned parallel to the laser

polarization axis. The results are shown in Fig. 3a, b. To help understanding, we plot the relevant molecular orbitals in Fig. 3c. Figure 3a presents hole densities extracted at the

recombination times of harmonics H15 to H26. Here, _t_ = 0 is when electron is born. In the figures, the frames are separated by steps of about 50 as. At a quick glance, we can see

substantial hole migration from +_x_ side to the −_x_ side over the 0.5 fs duration. To take a closer look at how the hole migrates, in Fig. 3b we zoom in the region of _x_ = [−1.2, 1.2]

a.u. In the first 0.25 fs, we can see that the hole density coalesces in the middle region along the _x_-axis slowly from the +_x_ side to the −_x_ side, but in the second half, the pace

turns faster where at later time we can see some density is moving back to the +_x_ side. In fact, its time evolution is more like a counterclockwise swirling than a direct migration. To

observe the continuous evolution of hole density, we have constructed movies at steps of 10 as by interpolating the mixing coefficients in the complex wave packets shown in Fig. 2e–h (see

Supplementary movie 1). Since quantum mechanics can predict single-hole behavior only statistically, it is inappropriate to associate such movement with trajectory or speed. It is more

proper to think such movement like that of a flock of migrating birds. Each bird has its own mind and there is nothing to govern the trajectory of each bird, yet the flock will move on. In

the presence of an external disturbance, the movement of the flock will change. So is the migration of an electron or a hole in the presence of the laser field. To describe the movement of

charge density of a quantum system, consider the equation of continuity, \(\frac{\partial {\rho }_{{{{{{{{\rm{e}}}}}}}}}}{\partial t}\) + ∇ ⋅ J = 0, where _ρ_e is the probability density and

J is the probability current density. By calculating them from the complex hole wave packet, we can obtain the total flux crossing the _x_ = 0 plane at each time instant, as shown by the

red line in Fig. 3d. We have confirmed that the total flux change is equal to the rate of change of the total charge density. Likewise, the total flux crossing the _y_ = 0 plane can be

calculated (the blue line). The total flux varies rapidly versus time, demonstrating attosecond dynamics. Our reconstruction method for each harmonic obtains the occupation amplitude and

phase for all angles of each fixed-in-space molecules. In Fig. 4a–c, we show a sample of hole density plots of CO2 molecule for alignment angles of 15°, 45°, and 90°, respectively. For the

same 0.5 fs duration, we can clearly see that the hole density does undergo significant change and vary significantly with alignment angles. These results prove that one should not obtain

single-molecule harmonic phase and amplitude directly from the experiment without angular deconvolution. In Fig. 4d, e we also calculated the total flux across the _x_ = 0 and _y_ = 0

planes, respectively, for the three angles. In Supplementary Movies 2, 3, 4 we show the movies of hole migration for these three angles. In Fig. 4f–h, we show the reconstructed hole

densities in N2 at several selected excursion times for the alignment angles of 0°, 60°, and 90°, respectively. The hole densities are symmetric about the _x_ = 0 plane for all alignment

angles because of the symmetry of the HOMO and HOMO-1 orbitals of N2. At 0° and 60°, only small migration can be seen, because HHG from HOMO-1 is weak. At 90°, HOMO-1 becomes important and

one can see faster change of charge density at later excursion time. These results are consistent with the time dependence of total flux across the _x_ = −1.5 a.u. and _y_ = 0 planes,

respectively, as shown in Fig. 4i, j. Note that the hole density is symmetric about the _x_ = 0 plane, thus the flux crossing the _x_ = 0 plane is very small. Hole migration for N2 has also

been constructed (see Supplementary Movies 5–8). In the constructed movies, the time span is associated with the excursion time of the harmonic orders (H15-H26 for CO2, and H15-H27 for N2)

used in the reconstruction, which is limited to approximately 0.94 fs to 1.5 fs for an 800-nm driving laser as illustrated in Fig. 1b. This time window can be further expanded by using a

long wavelength driving laser28. The extended time window of the molecular movie will help to capture the effect of nuclear motions on the electron dynamics at longer time. Comparing to

results previously reported by Kraus et al.28, we are able to make movies of laser-driven charge migration at steps of 10 as by interpolating the experimental data, for molecules at all

alignment angles. This is because we were able to retrieve single-molecule complex dipole at each fixed-in-space angle and probe charge migration at recombination times for both even and odd

harmonics at every 50 attoseconds, instead of 100 attoseconds if only odd harmonics are measured. With twice as many data points within the same interval, it is more accurate to

interpolate. Figure 3b has shown that such 10 as resolution is needed in order to follow the charge migration in CO2. Before closing, we mention that we have confirmed that charge migration

dynamics of single molecules constructed directly from experimental harmonic spectra would cause large errors (see Supplementary Note 6), and that charge migration under field-free condition

evolves slower than when electrons are under the intense laser field (See Supplementary Note 7). The latter is similar to the familiar field-free two-level oscillation is slower than the

Rabi oscillation when the two levels are driven by an intense laser pulse. In experiment, the influence of the strong laser field on the charge migration process may be reduced by using a

few-cycle fundamental pulse instead of a multi-cycle pulse. But in the few-cycle regime, it may increase the difficulty to build the time-frequency mapping due to the less sharp spectrum

structure of each individual harmonic. DISCUSSION In summary, we have used a ML-based HHS method to construct movies of laser-driven charge migration in a molecular ion at its natural

timescale of 10 as to follow the change of hole density during the time between electron is removed till it has recombined with the ion to emit harmonics. We presented the migration dynamics

at the most fundamental level for each single fixed-in-space molecule at all alignment angles from the experimental HHG spectra. The method presented here in principle can be extended to

other molecules, but in reality, it will be limited by the number of molecular orbitals in the wave packet. As the number of mixing parameters in the wave packet increases, larger amount of

experimental data would be needed for retrieval. Looking ahead, the method may be extended to other molecules where harmonic spectra have been well studied to identify other possible

migration pathways, for examples, in ring molecules. Finally, we want to emphasize that the method of retrieving single-molecule parameters used in the present work should be extended to

other ultrafast experiments, including tomography, time delays, photoelectron momentum spectra, just name a few, for any gas-phase targets where the experimental data are always resulting

from coherent or incoherent superposition of signals from individual single fixed-in-space molecules weighted by the angular distribution of the molecules. METHODS EXPERIMENTAL METHODS Our

experiment is carried out by using a commercial Ti:sapphire laser system (Legend Elite-Duo, Coherent, Inc.), which delivers 35-fs, 800-nm laser pulses at a repetition rate of 1 kHz. The

output laser is split into an alignment and a probe pulse. The alignment pulse with moderate intensity is used to induce nonadiabatic alignment of molecules along its polarization. The

intense probe pulse has been used either directly (one-color scheme) or remolded to a parallel two-color laser field (see Supplementary Note 1) to interact with the aligned molecules to

generate high-order harmonics. The alignment and probe pulses are parallel in the polarization. A motorized delay line is installed in the arm of the alignment pulse to adjust the time delay

between the two pulses. These two pulses are focused to a supersonic gas jet by a spherical mirror (_f_ = 250 mm). The gas jet is placed 2 mm after the laser focus to ensure good phase

matching for short-trajectory harmonics, and the backing pressure is maintained at 0.8 bar. The generated high harmonics are detected by a homemade flat-field soft x-ray spectrometer. In the

one-color experiment, the harmonic signals measured at different time delays [Fig. 1d and Supplementary Fig. 2e] are used to identify the multiple orbitals effect in HHG. In the two-color

experiment, the time-dependent harmonic signals are measured at various relative phases of the two-color laser field, providing a two-dimensional data set for decomposing the multiple

orbital contributions in HHG process. RECONSTRUCTION METHODS Our reconstruction procedure has two steps. The first step is to retrieve single-molecule dipole moment from the measured

time-dependent HHG signals. HHG from aligned molecular ensemble is expressed as Eq. (1). For a given harmonic order, Eq. (1) can be expanded as49,50 $$S(\tau )= {\left[\int\nolimits_{0}^{\pi

}D(\theta )\rho (\theta,\, \tau )\sin\theta {{{{{\rm{d}}}}}}\theta \right]}^{*}\left[\int\nolimits_{0}^{\pi }D(\theta )\rho (\theta,\, \tau )\sin\theta {{{{{\rm{d}}}}}}\theta \right]\\=

\int\nolimits_{0}^{\pi }\int\nolimits_{0}^{\pi }{D}{*}({\theta }_{1})D({\theta }_{2})\rho ({\theta }_{1},\, \tau )\rho ({\theta }_{2},\, \tau )\sin{\theta }_{1}\sin{\theta

}_{2}{{{{{\rm{d}}}}}}{\theta }_{1}{{{{{\rm{d}}}}}}{\theta }_{2}.$$ (2) Let $$R({\theta }_{1},\, {\theta }_{2})={{{{{\rm{Re}}}}}}[{D}^{*}({\theta }_{1})D({\theta }_{2})],$$ (3) $$\rho

({\theta }_{1},\, {\theta }_{2},\, \tau )=\rho ({\theta }_{1},\, \tau )\rho ({\theta }_{2},\, \tau )\sin{\theta }_{1}\sin{\theta }_{2},$$ (4) and discretize _θ_1, _θ_2 in the range of [0,

_π_] with a step of 0.01 rad, the _S_(_τ_) then can be rewritten as $$S(\tau )=\mathop{\sum}\limits_{p}\mathop{\sum}\limits_{q}R({\theta }_{1}^{p},\, {\theta }_{2}^{q})\rho ({\theta

}_{1}^{p},\, {\theta }_{2}^{q},\, \tau ){{{{{\rm{d}}}}}}{\theta }_{1}{{{{{\rm{d}}}}}}{\theta }_{2}.$$ (5) Note that in Eq. (3), the imaginary part of _D_*(_θ_1)_D_(_θ_2) is omitted due to

its asymmetry upon the exchange of _θ_1 and _θ_2, which will vanish after the convolution. In Eqs. (2) and (4), the molecular axis distribution _ρ_(_θ_, _τ_) and therefore _ρ_(_θ_1, _θ_2, 

_τ_) can be determined from the one-color experiment with the method in44. To retrieve single-molecule dipole moment _D_(_θ_), we first solve the matrix _R_(_θ_1, _θ_2) according to Eq. (5).

Here, we utilize a widely-used ML algorithm, sparse representation51, to do the retrieval. In the reconstruction, we first build a dictionary matrix for _S_(_τ_) by expanding the _R_ matrix

with a series of two-dimensional Legendre polynomial basis functions. The expansion coefficients then can be solved with the LASSO regression52 by minimizing the _l_1-norm of the

coefficient vector and also the difference between the reproductions and the measurements. With _R_(_θ_1, _θ_2) retrieved, we can obtain the amplitude and phase of the dipole moment _D_(_θ_)

in terms of the derivations of Eq. (3). The validity and robustness of this algorithm have been validated by simulation experiments (see Supplementary Note 4). Applying this procedure to

measurements at different relative phases _α_ of the two-color laser field, we can get a set of _D_(_θ_; _α_) for each harmonic order. The second step of the reconstruction is to decompose

the multichannel contributions from the total dipole moment _D_(_θ_; _α_) obtained in the first step. In molecular HHG, the total dipole moment _D_(_ω_, _θ_) is a coherent superposition of

the induced dipole moment of each emission channel, i.e., $$D(\omega,\, \theta )=\mathop{\sum}\limits_{i}{D}_{i}(\omega,\, \theta ),$$ (6) where _D__i_(_ω_, _θ_) is the induced dipole moment

of each emission channel. The subscript _i_ denotes the involved molecular orbitals (molecular ion states) during the HHG process. Consider the initially populated molecular ion state _i_,

_D__i_(_ω_, _θ_) is given by $${D}_{i}(\omega,\, \theta )={d}_{{{{{{{{\rm{ion}}}}}}}}}^{i}(\omega,\, \theta ){a}_{{{{{{{{\rm{acc}}}}}}}}}^{i}(\omega

){d}_{{{{{{{{\rm{rec}}}}}}}}}^{i}(\omega,\, \theta ),$$ (7) where \({d}_{{{{{{{{\rm{ion}}}}}}}}}^{i}(\omega,\, \theta )\) and \({d}_{{{{{{{{\rm{rec}}}}}}}}}^{i}(\omega,\, \theta )\) are the

transition dipole moments related to the ionization and recombination steps, respectively. \({a}_{{{{{{{{\rm{acc}}}}}}}}}^{i}(\omega )\) denotes the propagation amplitude of the EWP in the

continuum. \({d}_{{{{{{\rm{ion}}}}}}}^{i}(\omega,\, \theta )\) can be expressed as $${d}_{{{{{{{{\rm{ion}}}}}}}}}^{i}=\sqrt{{\eta }_{i}}\langle {{{\Psi }}}_{0}(N)|\tilde{D}|{{{\Phi

}}}_{i}(N-1){\chi }_{k}\rangle$$ (8a) $$=\sqrt{{\eta }_{i}}\langle {\psi }_{i}|r|{\chi }_{k}\rangle .$$ (8b) Here _η__i_ is the ionization rate, Ψ0(_N_) is the ground state of the N-electron

molecule, Φ_i_(_N_−1) is the ground state or excited state of the (N-1)-electron molecular ion, where a molecular orbital _ψ__i_ has been removed to a continuum state _χ__k_. Both

many-electron wavefunctions Ψ0(_N_) and Φ_i_(_N_ − 1)_χ__k_ are properly antisymmetrized and \(\tilde{D}\) is the dipole operator from all the electrons. In obtaining Eq. (8b), we assume

that all the molecular orbitals are in the neutral and the ion does not change before and after ionization. To calculate the recombination transition dipole, we take into account that the

molecular ion has been modified by the laser field during the time interval between ionization and recombination to \({{{\Phi }}}_{i}^{\prime}(N-1)\), where $${{{\Phi

}}}_{i}^{\prime}(N-1)=\mathop{\sum}\limits_{j}{C}_{ij}(\theta ){{{\Phi }}}_{j}(N-1).$$ (9) Thus, the recombination dipole $${d}_{{{{{{{{\rm{rec}}}}}}}}}^{i} =\langle {{{\Phi

}}}_{i}^{\prime}(N-1){\chi }_{k}|\tilde{D}|{{{\Psi }}}_{0}(N)\rangle \\ =\mathop{\sum}\limits_{j}{C}_{ij}(\theta )\langle {\chi }_{k}|r|{\psi }_{j}\rangle .$$ (10) Inserting Eq. (10) to Eq.

(7), we obtain $${D}_{i}(\omega,\, \theta )=\mathop{\sum}\limits_{j}{C}_{ij}(\theta ){d}_{{{{{{{{\rm{ion}}}}}}}}}^{i}(\omega,\, \theta ){a}_{{{{{{{{\rm{acc}}}}}}}}}^{i}(\omega

){d}_{{{{{{{{\rm{rec}}}}}}}}}^{j}(\omega,\, \theta ).$$ (11) Eq. (11) implies that hole hopping occurs before recombination. The degree of hopping depends on laser parameter and the

alignment angle _θ_ of the molecule. With Eq. (11), the total dipole moment for HHG can be expressed as $$D(\omega,\, \theta )=\mathop{\sum}\limits_{ij}{C}_{ij}(\theta

){\bar{D}}_{ij}(\omega,\, \theta ),$$ (12) where $${\bar{D}}_{ij}(\omega,\, \theta )={d}_{{{{{{{{\rm{ion}}}}}}}}}^{i}(\omega,\, \theta ){a}_{{{{{{{{\rm{acc}}}}}}}}}^{i}(\omega

){d}_{{{{{{{{\rm{rec}}}}}}}}}^{j}(\omega,\, \theta ).$$ (13) In our reconstruction, only the most relevant molecular orbitals _ψ__j_ are considered (that is, \(\tilde{X}\) and \(\tilde{A}\)

states for N2, and \(\tilde{X}\), \(\tilde{A}\), and \(\tilde{B}\) states for CO2). The dipole moment \({\bar{D}}_{ij}(\omega,\, \theta )\) is calculated under the experimental laser

conditions. The complex-valued coefficients _C__i__j_(_θ_) are directly associated with the electron dynamics in the molecular ion. To determine _C__i__j_(_θ_), we have performed two-color

experiment. Since the SH field in the two-color experiment is weak enough and hardly alters the laser-driven electron dynamics, the coefficients _C__i__j_(_θ_) can be assumed to be

independent of the relative phase _α_. The coefficients _C__i__j_(_θ_) are then retrieved from the dipole moment _D_(_θ_; _α_) obtained at different relative phases _α_ by solving Eq. (12)

with the genetic algorithm. With the coefficients _C__i__j_(_θ_) retrieved, we can further calculate the wavefunction of the molecular ion at the recombination instant as $${\psi

}_{{{{{{{{\rm{sum}}}}}}}}}=\mathop{\sum}\limits_{i}{\gamma }_{i}(\theta ){\psi }_{i}^{\prime}=\mathop{\sum}\limits_{i}\mathop{\sum}\limits_{j}{\gamma }_{i}(\theta ){C}_{ij}(\theta ){\psi

}_{j},$$ (14) and the population coefficient of the molecular orbital _ψ__j_ as28 $${p}_{j}=\mathop{\sum}\limits_{i}{C}_{ij}(\theta ){\gamma }_{i}(\theta ),$$ (15) where _γ__i_(_θ_) is the

initial population of the molecular ion state _i_, which is related to the alignment-angle-dependent ionization rate _η__i_(_θ_) by ∣_γ__i_(_θ_)∣2 = _η__i_(_θ_)/Σ_i__η__i_(_θ_). In our work,

the alignment-angle-dependent ionization rates of each molecular orbital are simulated by the MO-ADK theory53,54. Repeating the above procedure for different harmonic orders, we can then

construct the hole dynamics in the ionized molecular ion according to time-frequency mapping underlying the HHG process. DATA AVAILABILITY All the data that support the findings of this

study are available from the corresponding author upon reasonable request. CODE AVAILABILITY All the codes that support the findings of this study are available from the corresponding author

upon reasonable request. REFERENCES * Cederbaum, L. S. & Zobeley, J. Ultrafast charge migration by electron correlation. _Chem. Phys. Lett._ 307, 205–210 (1999). Article  ADS  CAS 

Google Scholar  * Breidbacha, J. & Cederbaum, L. S. Migration of holes: formalism, mechanisms, and illustrative applications. _J. Chem. Phys._ 118, 3983 (2003). Article  ADS  CAS  Google

Scholar  * Calegari, F. et al. Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses. _Science_ 346, 336–339 (2014). Article  ADS  CAS  PubMed  Google Scholar  *

Kraus, P. M. & Wörner, H. J. Perspectives of attosecond spectroscopy for the understanding of fundamental electron correlations. _Angew. Chemie. Int. Ed._ 57, 5228–5247 (2018). Article 

CAS  Google Scholar  * Kuleff, A. I., Lünnemann, S. & Cederbaum, L. S. Electron-correlation-driven charge migration in oligopeptides. _Chem. Phys._ 414, 100–105 (2013). Article  CAS 

Google Scholar  * Lünnemann, S., Kuleff, A. I. & Cederbaum, L. S. Ultrafast charge migration in 2-phenylethyl-N,N-dimethylamine. _Chem. Phys. Lett._ 450, 232–235 (2008). Article  ADS 

CAS  Google Scholar  * Folorunso, A. S. et al. Molecular modes of attosecond charge migration. _Phys. Rev. Lett._ 126, 133002 (2021). Article  ADS  CAS  PubMed  Google Scholar  * Paul, P. M.

et al. Observation of a train of attosecond pulses from high harmonic generation. _Science_ 292, 1689 (2001). Article  ADS  CAS  PubMed  Google Scholar  * Hentschel, M. et al. Attosecond

metrology. _Nature_ 414, 509 (2001). Article  ADS  CAS  PubMed  Google Scholar  * Krausz, F. & Ivanov, M. Attosecond physics. _Rev. Mod. Phys._ 81, 163 (2009). Article  ADS  Google

Scholar  * Goulielmakis, E. et al. Real-time observation of valence electron motion. _Nature_ 466, 739743 (2010). Article  CAS  Google Scholar  * Wang, H. et al. Attosecond time-resolved

autoionization of argon. _Phys. Rev. Lett._ 105, 143002 (2010). Article  ADS  PubMed  CAS  Google Scholar  * Drescher,, M. et al. Time-resolved atomic inner-shell spectroscopy. _Nature_ 419,

803 (2002). Article  ADS  CAS  Google Scholar  * Sansone, G. et al. Electron localization following attosecond molecular photoionization. _Nature_ 465, 763 (2010). Article  ADS  CAS  PubMed

  Google Scholar  * Williamson, J., Cao, J., Ihee, H., Frey, H. & Zewail, A. Clocking transient chemical changes by ultrafast electron diffraction. _Nature_ 386, 159–162 (1997). Article

  ADS  CAS  Google Scholar  * Yang, J. et al. Simultaneous observation of nuclear and electronic dynamics by ultrafast electron diffraction. _Science_ 368, 885–889 (2020). Article  ADS  CAS

  PubMed  Google Scholar  * Baum, P. & Zewail, A. Breaking resolution limits in ultrafast electron diffraction and microscopy. _Proc. Natl. Acad. Sci. USA_ 103, 16105–16110 (2006).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Leone, S. R. et al. What will it take to observe processes in ‘real time’? _Nat. Photon._ 8, 162–166 (2014). Article  ADS  CAS 

Google Scholar  * Lépine, F., Ivanov, M. & Vrakking, M. Attosecond molecular dynamics: fact or fiction? _Nat. Photon._ 8, 195–204 (2014). Article  ADS  CAS  Google Scholar  * Corkum, P.

B. Plasma perspective on strong field multiphoton ionization. _Phys. Rev. Lett._ 71, 1994 (1993). Article  ADS  CAS  PubMed  Google Scholar  * Lewenstein, M., Balcou, P. H., Ivanov, M.,

L’Huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. _Phys. Rev. A_ 49, 2117 (1994). Article  ADS  CAS  PubMed  Google Scholar  * Blaga, C. I.

et al. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. _Nature_ 483, 194–197 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Wolter, B. et al. Ultrafast

electron diffraction imaging of bond breaking in di-ionized acetylene. _Science_ 354, 308 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Amini, K. et al. Imaging the Renner-Teller

effect using laser-induced electron diffraction. _Proc. Natl. Acad. Sci. USA_ 116, 8173 (2019). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Sanchez, A. et al. Molecular

structure retrieval directly from laboratory-frame photoelectron spectra in laser-induced electron diffraction. _Nat. Commun._ 12, 1–9 (2021). Article  CAS  Google Scholar  * Lein, M.

Attosecond probing of vibrational dynamics with high-harmonic generation. _Phys. Rev. Lett._ 94, 053004 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Baker, S. et al. Probing proton

dynamics in molecules on an attosecond time scale. _Science_ 312, 424 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Kraus, P. M. et al. Measurement and laser control of attosecond

charge migration in ionized iodoacetylene. _Science_ 350, 790 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Itatani, J. et al. Tomographic imaging of molecular orbitals. _Nature_ 432,

867 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Haessler, S. et al. Attosecond imaging of molecular electronic wavepackets. _Nat. Phys._ 6, 200 (2010). Article  CAS  Google Scholar

  * Peng, P., Marceau, C. & Villeneuve, D. M. Attosecond imaging of molecules using high harmonic spectroscopy. _Nat. Rev. Physics_ 1, 144–155 (2019). Article  ADS  Google Scholar  *

Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft x-rays. _Science_ 302, 1540 (2003). Article  ADS  CAS  PubMed  Google Scholar  * He, L. et al. Real-time observation of

molecular spinning with angular high-harmonic spectroscopy. _Phys. Rev. Lett._ 121, 163201 (2018). Article  ADS  CAS  PubMed  Google Scholar  * He, Y. et al. Direct imaging of molecular

rotation with high-order-harmonic generation. _Phys. Rev. A_ 99, 053419 (2019). Article  ADS  CAS  Google Scholar  * Yoshii, K., Miyaji, G. & Miyazaki, K. Retrieving angular

distributions of high-order harmonic generation from a single molecule. _Phys. Rev. Lett._ 106, 013904 (2011). Article  ADS  PubMed  CAS  Google Scholar  * Smirnova, O. et al. High harmonic

interferometry of multi-electron dynamics in molecules. _Nature_ 460, 972 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Smirnova, O., Patchkovskii, S., Mairesse, Y., Dudovich, N.

& Ivanov, M. Y. Strong-field control and spectroscopy of attosecond electron-hole dynamics in molecules. _Proc. Natl. Acad. Sci. USA_ 106, 16556 (2009). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Mairesse, Y. et al. High harmonic spectroscopy of multichannel dynamics in strong-field ionization. _Phys. Rev. Lett._ 104, 213601 (2010). Article  ADS  CAS 

PubMed  Google Scholar  * McFarland, B. K., Farrell, J. P., Bucksbaum, P. H. & Gühr, M. High harmonic generation from multiple orbitals in N2. _Science_ 322, 1232–1235 (2008). Article 

ADS  CAS  PubMed  Google Scholar  * Le, A. T., Lucchese, R. R., Tonzani, S., Morishita, T. & Lin, C. D. Quantitative rescattering theory for high-order harmonic generation from

molecules. _Phys. Rev. A_ 80, 013401 (2009). Article  ADS  CAS  Google Scholar  * Lin, C. D., Le, A. T., Chen, Z., Morishita, T. & Lucchese, R. Strong-field rescattering

physics—self-imaging of a molecule by its own electrons. _J. Phys. B: At. Mol. Opt. Phys._ 43, 122001 (2010). Article  ADS  CAS  Google Scholar  * Lin, C. D., Le, A. T., Jin, C. & Wei,

H. _Attosecond and Strong-Field Physics: Principles and Applications_ (Cambridge University Press, 2018). * Lin, C. D., Le, A. T., Jin, C. & Wei, H. Elements of the quantitative

rescattering Theory. _J. Phys. B: At. Mol. Opt. Phys._ 51, 104001 (2018). Article  ADS  CAS  Google Scholar  * He, Y. et al. Measuring the rotational temperature and pump intensity in

molecular alignment experiments via high harmonic generation. _Opt. Express_ 28, 21182–21191 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Libbrecht, M. W. & Noble, W. S. Machine

learning applications in genetics and genomics. _Nat. Rev. Genet._ 16, 321 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Carrasquilla, J. & Melko, R. G. Machine

learning phases of matter. _Nat. Phys._ 13, 431 (2017). Article  CAS  Google Scholar  * Raccuglia, P. et al. Machine-learning-assisted materials discovery using failed experiments. _Nature_

533, 73 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Dudovich, N. et al. Measuring and controlling the birth of attosecond XUV pulses. _Nat. Phys._ 2, 781 (2006). Article  CAS 

Google Scholar  * Wang, X., Le, A., Zhou, Z., Wei, H. & Lin, C. D. Theory of retrieving orientation-resolved molecular information using time-domain rotational coherence spectroscopy.

_Phys. Rev. A_ 96, 023424 (2017). Article  ADS  Google Scholar  * Wang, B. et al. Retrieval of full angular- and energy-dependent complex transition dipoles in the molecular frame from

laser-induced high-order harmonic signals with aligned molecules. _Phys. Rev. A_ 101, 063417 (2020). Article  ADS  CAS  Google Scholar  * Rubinstein, R., Bruckstein, A. M. & Elad, M.

Dictionaries for sparse representation modeling. _Proc. IEEE_ 98, 1045–1057 (2010). Article  Google Scholar  * Tibshirani, R. Regression Shrinkage and Selection via the Lasso. _J. R.

Statistical Soc. Ser. B_ 58, 267–288 (1996). MathSciNet  MATH  Google Scholar  * Tong, X. M., Zhao, Z. X. & Lin, C. D. Theory of molecular tunneling ionization. _Phys. Rev. A_ 66, 033402

(2002). Article  ADS  CAS  Google Scholar  * Tong, X. M. & Lin, C. D. Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression

regime. _J. Phys. B: At. Mol. Opt. Phys._ 38, 2593 (2005). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by fundings from the National Key

Research and Development Program of China (No. 2019YFA0308300 (L.X.H.), 2017YFE0116600 (P.F.L.)), National Natural Science Foundation of China (No. 91950202 (P.F.L.), 12074136 (L.X.H.),

12021004 (P.X.L.), 11627809 (P.F.L. and P.X.L.), 11934006 (P.F.L. and P.X.L.)), and Natural Science Foundation of Hubei Province (No. (2021CFB330 (L.X.H)). C.D.L. was supported by Chemical

Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy under Grant No. DE-FG02-86ER13491. C.D.L. would like to thank

Professor H. Wörner for initial communications on charge migration. AUTHOR INFORMATION Author notes * These authors contributed equally: Lixin He, Siqi Sun. AUTHORS AND AFFILIATIONS * Wuhan

National Laboratory for Optoelectronics and School of Physics, Huazhong University of Science and Technology, 430074, Wuhan, China Lixin He, Siqi Sun, Pengfei Lan, Yanqing He, Bincheng Wang,

 Pu Wang, Xiaosong Zhu, Liang Li, Wei Cao & Peixiang Lu * Optical Valley Laboratory, 430074, Hubei, China Lixin He, Pengfei Lan, Xiaosong Zhu, Liang Li, Wei Cao & Peixiang Lu * CAS

Center for Excellence in Ultra-intense Laser Science, 201800, Shanghai, China Peixiang Lu * Department of Physics, Cardwell Hall, Kansas State University, Manhattan, KS, 66506, USA C. D. Lin

Authors * Lixin He View author publications You can also search for this author inPubMed Google Scholar * Siqi Sun View author publications You can also search for this author inPubMed 

Google Scholar * Pengfei Lan View author publications You can also search for this author inPubMed Google Scholar * Yanqing He View author publications You can also search for this author

inPubMed Google Scholar * Bincheng Wang View author publications You can also search for this author inPubMed Google Scholar * Pu Wang View author publications You can also search for this

author inPubMed Google Scholar * Xiaosong Zhu View author publications You can also search for this author inPubMed Google Scholar * Liang Li View author publications You can also search for

this author inPubMed Google Scholar * Wei Cao View author publications You can also search for this author inPubMed Google Scholar * Peixiang Lu View author publications You can also search

for this author inPubMed Google Scholar * C. D. Lin View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS P.F.L. and P.X.L. conceived this

research. L.X.H., Y.Q.H., and P.W. performed the experiments. S.Q.S. developed the reconstruction algorithm. L.X.H. and Y.Q.H. performed the simulations. C.D.L., L.X.H., and P.F.L. analyzed

the data and wrote the manuscript. B.C.W., X.S.Z., L.L., and W.C. participated in the discussions. CORRESPONDING AUTHORS Correspondence to Pengfei Lan or Peixiang Lu. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Tomoya Okino and the other anonymous, reviewer(s) for their

contribution to the peer review of this work. Peer reviewer reports are available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY

MOVIE 1 SUPPLEMENTARY MOVIE 2 SUPPLEMENTARY MOVIE 3 SUPPLEMENTARY MOVIE 4 SUPPLEMENTARY MOVIE 5 SUPPLEMENTARY MOVIE 6 SUPPLEMENTARY MOVIE 7 SUPPLEMENTARY MOVIE 8 RIGHTS AND PERMISSIONS OPEN

ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format,

as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third

party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE He, L., Sun, S., Lan, P. _et al._

Filming movies of attosecond charge migration in single molecules with high harmonic spectroscopy. _Nat Commun_ 13, 4595 (2022). https://doi.org/10.1038/s41467-022-32313-0 Download citation

* Received: 11 August 2021 * Accepted: 26 July 2022 * Published: 06 August 2022 * DOI: https://doi.org/10.1038/s41467-022-32313-0 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative