The medial entorhinal cortex is necessary for temporal organization of hippocampal neuronal activity

ABSTRACT The superficial layers of the medial entorhinal cortex (MEC) are a major input to the hippocampus. The high proportion of spatially modulated cells, including grid cells and border

cells, in these layers suggests that MEC inputs are critical for the representation of space in the hippocampus. However, selective manipulations of the MEC do not completely abolish

hippocampal spatial firing. To determine whether other hippocampal firing characteristics depend more critically on MEC inputs, we recorded from hippocampal CA1 cells in rats with MEC

lesions. Theta phase precession was substantially disrupted, even during periods of stable spatial firing. Our findings indicate that MEC inputs to the hippocampus are required for the

temporal organization of hippocampal firing patterns and suggest that cognitive functions that depend on precise neuronal sequences in the hippocampal theta cycle are particularly dependent

on the MEC. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your institution Subscribe

to this journal Receive 12 print issues and online access $209.00 per year only $17.42 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF

Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact

customer support SIMILAR CONTENT BEING VIEWED BY OTHERS DISTINCT ROLES OF DENTATE GYRUS AND MEDIAL ENTORHINAL CORTEX INPUTS FOR PHASE PRECESSION AND TEMPORAL CORRELATIONS IN THE HIPPOCAMPAL

CA3 AREA Article Open access 02 January 2025 THE MEDIAL SEPTUM CONTROLS HIPPOCAMPAL SUPRA-THETA OSCILLATIONS Article Open access 10 October 2023 A DIRECT EXCITATORY PROJECTION FROM

ENTORHINAL LAYER 6B NEURONS TO THE HIPPOCAMPUS CONTRIBUTES TO SPATIAL CODING AND MEMORY Article Open access 16 August 2022 REFERENCES * Quirk, G.J., Muller, R.U., Kubie, J.L. & Ranck,

J.B. Jr. The positional firing properties of medial entorhinal neurons: description and comparison with hippocampal place cells. _J. Neurosci._ 12, 1945–1963 (1992). Article  CAS  PubMed 

PubMed Central  Google Scholar  * Hafting, T., Fyhn, M., Molden, S., Moser, M.B. & Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. _Nature_ 436, 801–806 (2005).

Article  CAS  PubMed  Google Scholar  * Sargolini, F. et al. Conjunctive representation of position, direction and velocity in entorhinal cortex. _Science_ 312, 758–762 (2006). Article  CAS

  PubMed  Google Scholar  * Solstad, T., Boccara, C.N., Kropff, E., Moser, M.B. & Moser, E.I. Representation of geometric borders in the entorhinal cortex. _Science_ 322, 1865–1868

(2008). Article  CAS  PubMed  Google Scholar  * Zhang, S.J. et al. Optogenetic dissection of entorhinal-hippocampal functional connectivity. _Science_ 340, 1232627 (2013). Article  PubMed 

CAS  Google Scholar  * Brandon, M.P. et al. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. _Science_ 332, 595–599 (2011). Article  CAS  PubMed 

PubMed Central  Google Scholar  * Brandon, M.P., Koenig, J., Leutgeb, J.K. & Leutgeb, S. New and distinct hippocampal place codes are generated in a new environment during septal

inactivation. _Neuron_ 82, 789–796 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Koenig, J., Linder, A.N., Leutgeb, J.K. & Leutgeb, S. The spatial periodicity of grid

cells is not sustained during reduced theta oscillations. _Science_ 332, 592–595 (2011). Article  CAS  PubMed  Google Scholar  * Wang, Y., Romani, S., Lustig, B., Leonardo, A. &

Pastalkova, E. Theta sequences are essential for internally generated hippocampal firing fields. _Nat. Neurosci._ 18, 282–288 (2015). Article  CAS  PubMed  Google Scholar  * Hales, J.B. et

al. Medial entorhinal cortex lesions only partially disrupt hippocampal place cells and hippocampus-dependent place memory. _Cell Rep._ 9, 893–901 (2014). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Deshmukh, S.S., Yoganarasimha, D., Voicu, H. & Knierim, J.J. Theta modulation in the medial and the lateral entorhinal cortices. _J. Neurophysiol._ 104,

994–1006 (2010). Article  PubMed  PubMed Central  Google Scholar  * O'Keefe, J. & Recce, M.L. Phase relationship between hippocampal place units and the EEG theta rhythm.

_Hippocampus_ 3, 317–330 (1993). Article  CAS  PubMed  Google Scholar  * Hafting, T., Fyhn, M., Bonnevie, T., Moser, M.B. & Moser, E.I. Hippocampus-independent phase precession in

entorhinal grid cells. _Nature_ 453, 1248–1252 (2008). Article  CAS  PubMed  Google Scholar  * Mizuseki, K., Sirota, A., Pastalkova, E. & Buzsaki, G. Theta oscillations provide temporal

windows for local circuit computation in the entorhinal-hippocampal loop. _Neuron_ 64, 267–280 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Skaggs, W.E., McNaughton, B.L.,

Wilson, M.A. & Barnes, C.A. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. _Hippocampus_ 6, 149–172 (1996). Article  CAS  PubMed 

Google Scholar  * Jensen, O. & Lisman, J.E. Hippocampal CA3 region predicts memory sequences: accounting for the phase precession of place cells. _Learn. Mem._ 3, 279–287 (1996). Article

  CAS  PubMed  Google Scholar  * Melamed, O., Gerstner, W., Maass, W., Tsodyks, M. & Markram, H. Coding and learning of behavioral sequences. _Trends Neurosci._ 27, 11–14, discussion

14–15 (2004). Article  CAS  PubMed  Google Scholar  * Dragoi, G. & Buzsaki, G. Temporal encoding of place sequences by hippocampal cell assemblies. _Neuron_ 50, 145–157 (2006). Article 

CAS  PubMed  Google Scholar  * Bi, G. & Poo, M. Synaptic modification by correlated activity: Hebb's postulate revisited. _Annu. Rev. Neurosci._ 24, 139–166 (2001). Article  CAS 

PubMed  Google Scholar  * Byrnes, S., Burkitt, A.N., Grayden, D.B. & Meffin, H. Learning a sparse code for temporal sequences using STDP and sequence compression. _Neural Comput._ 23,

2567–2598 (2011). Article  PubMed  Google Scholar  * Tsodyks, M.V., Skaggs, W.E., Sejnowski, T.J. & McNaughton, B.L. Population dynamics and theta rhythm phase precession of hippocampal

place cell firing: A spiking neuron model. _Hippocampus_ 6, 271–280 (1996). Article  CAS  PubMed  Google Scholar  * Robbe, D. & Buzsaki, G. Alteration of theta timescale dynamics of

hippocampal place cells by a cannabinoid is associated with memory impairment. _J. Neurosci._ 29, 12597–12605 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Gupta, A.S., van

der Meer, M.A., Touretzky, D.S. & Redish, A.D. Segmentation of spatial experience by hippocampal theta sequences. _Nat. Neurosci._ 15, 1032–1039 (2012). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Hasselmo, M.E., Bodelon, C. & Wyble, B.P. A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior

learning. _Neural Comput._ 14, 793–817 (2002). Article  PubMed  Google Scholar  * Zugaro, M.B., Monconduit, L. & Buzsaki, G. Spike phase precession persists after transient

intrahippocampal perturbation. _Nat. Neurosci._ 8, 67–71 (2005). Article  CAS  PubMed  Google Scholar  * Moser, E.I. et al. A test of the reverberatory activity hypothesis for hippocampal

'place' cells. _Neuroscience_ 130, 519–526 (2005). Article  CAS  PubMed  Google Scholar  * Mehta, M.R. Neuronal dynamics of predictive coding. _Neuroscientist_ 7, 490–495 (2001).

Article  CAS  PubMed  Google Scholar  * Harvey, C.D., Collman, F., Dombeck, D.A. & Tank, D.W. Intracellular dynamics of hippocampal place cells during virtual navigation. _Nature_ 461,

941–946 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Harris, K.D. et al. Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells.

_Nature_ 417, 738–741 (2002). Article  CAS  PubMed  Google Scholar  * Mehta, M.R., Lee, A.K. & Wilson, M.A. Role of experience and oscillations in transforming a rate code into a

temporal code. _Nature_ 417, 741–746 (2002). Article  CAS  PubMed  Google Scholar  * Miller, V.M. & Best, P.J. Spatial correlates of hippocampal unit activity are altered by lesions of

the fornix and endorhinal cortex. _Brain Res._ 194, 311–323 (1980). Article  CAS  PubMed  Google Scholar  * Van Cauter, T., Poucet, B. & Save, E. Unstable CA1 place cell representation

in rats with entorhinal cortex lesions. _Eur. J. Neurosci._ 27, 1933–1946 (2008). Article  PubMed  Google Scholar  * Ylinen, A. et al. Intracellular correlates of hippocampal theta rhythm in

identified pyramidal cells, granule cells, and basket cells. _Hippocampus_ 5, 78–90 (1995). Article  CAS  PubMed  Google Scholar  * Kamondi, A., Acsady, L., Wang, X.J. & Buzsaki, G.

Theta oscillations in somata and dendrites of hippocampal pyramidal cells _in vivo_: activity-dependent phase-precession of action potentials. _Hippocampus_ 8, 244–261 (1998). Article  CAS 

PubMed  Google Scholar  * Kempter, R., Leibold, C., Buzsaki, G., Diba, K. & Schmidt, R. Quantifying circular-linear associations: hippocampal phase precession. _J. Neurosci. Methods_

207, 113–124 (2012). Article  PubMed  Google Scholar  * Maurer, A.P., Cowen, S.L., Burke, S.N., Barnes, C.A. & McNaughton, B.L. Organization of hippocampal cell assemblies based on theta

phase precession. _Hippocampus_ 16, 785–794 (2006). Article  PubMed  Google Scholar  * Huxter, J., Burgess, N. & O'Keefe, J. Independent rate and temporal coding in hippocampal

pyramidal cells. _Nature_ 425, 828–832 (2003). Article  CAS  PubMed  PubMed Central  Google Scholar  * Huxter, J.R., Senior, T.J., Allen, K. & Csicsvari, J. Theta phase–specific codes

for two-dimensional position, trajectory and heading in the hippocampus. _Nat. Neurosci._ 11, 587–594 (2008). Article  CAS  PubMed  Google Scholar  * Hargreaves, E.L., Rao, G., Lee, I. &

Knierim, J.J. Major dissociation between medial and lateral entorhinal input to dorsal hippocampus. _Science_ 308, 1792–1794 (2005). Article  CAS  PubMed  Google Scholar  * Aghajan, Z.M. et

al. Impaired spatial selectivity and intact phase precession in two-dimensional virtual reality. _Nat. Neurosci._ 18, 121–128 (2015). Article  CAS  PubMed  Google Scholar  * Lengyel, M.,

Szatmary, Z. & Erdi, P. Dynamically detuned oscillations account for the coupled rate and temporal code of place cell firing. _Hippocampus_ 13, 700–714 (2003). Article  PubMed  Google

Scholar  * Thurley, K., Leibold, C., Gundlfinger, A., Schmitz, D. & Kempter, R. Phase precession through synaptic facilitation. _Neural Comput._ 20, 1285–1324 (2008). Article  PubMed 

Google Scholar  * Magee, J.C. Dendritic mechanisms of phase precession in hippocampal CA1 pyramidal neurons. _J. Neurophysiol._ 86, 528–532 (2001). Article  CAS  PubMed  Google Scholar  *

Ekstrom, A.D., Meltzer, J., McNaughton, B.L. & Barnes, C.A. NMDA receptor antagonism blocks experience-dependent expansion of hippocampal “place fields”. _Neuron_ 31, 631–638 (2001).

Article  CAS  PubMed  Google Scholar  * Klausberger, T. et al. Complementary roles of cholecystokinin- and parvalbumin-expressing GABAergic neurons in hippocampal network oscillations. _J.

Neurosci._ 25, 9782–9793 (2005). Article  CAS  PubMed  PubMed Central  Google Scholar  * Feng, T., Silva, D. & Foster, D.J. Dissociation between the experience-dependent development of

hippocampal theta sequences and single-trial phase precession. _J. Neurosci._ 35, 4890–4902 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Jaramillo, J., Schmidt, R. &

Kempter, R. Modeling inheritance of phase precession in the hippocampal formation. _J. Neurosci._ 34, 7715–7731 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Harris, K.D.,

Hirase, H., Leinekugel, X., Henze, D.A. & Buzsaki, G. Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. _Neuron_ 32, 141–149 (2001).

Article  CAS  PubMed  Google Scholar  * Chance, F.S. Hippocampal phase precession from dual input components. _J. Neurosci._ 32, 16693–16703 (2012). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Leung, L.S. A model of intracellular theta phase precession dependent on intrinsic subthreshold membrane currents. _J. Neurosci._ 31, 12282–12296 (2011). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Schlesiger, M.I. et al. Hippocampal activation during the recall of remote spatial memories in radial maze tasks. _Neurobiol. Learn. Mem._ 106,

324–333 (2013). Article  CAS  PubMed  Google Scholar  * Bragin, A., Jando, G., Nadasdy, Z., van Landeghem, M. & Buzsaki, G. Dentate EEG spikes and associated interneuronal population

bursts in the hippocampal hilar region of the rat. _J. Neurophysiol._ 73, 1691–1705 (1995). Article  CAS  PubMed  Google Scholar  * Schmitzer-Torbert, N., Jackson, J., Henze, D., Harris, K.

& Redish, A.D. Quantitative measures of cluster quality for use in extracellular recordings. _Neuroscience_ 131, 1–11 (2005). Article  CAS  PubMed  Google Scholar  * Skaggs, W.E.,

McNaughton, B.L., Gothard, K.M. & Markus, E.J. An information-theoretic approach to deciphering the hippocampal code. in _Advances in Neural Information Processing Systems 5_ (eds.

Hanson, S.J., Giles, C.L. & Cowan, J.D.) 1030–1037 (Morgan Kaufmann, San Mateo, CA, 1993). * Bokil, H., Andrews, P., Kulkarni, J.E., Mehta, S. & Mitra, P.P. Chronux: a platform for

analyzing neural signals. _J. Neurosci. Methods_ 192, 146–151 (2010). Article  PubMed  PubMed Central  Google Scholar  * Jammalamadaka, S.R. & SenGupta, A. _Topics in Circular

Statistics_ (World Scientific, Singapore, 2001). Download references ACKNOWLEDGEMENTS The authors thank M. Wong for technical assistance, G. Diehl for recording control data and J. Lisman

for comments on the manuscript. This work was supported by a Boehringer Ingelheim Fonds PhD fellowship, the German Research Association (DFG) under grant LE 2250/5-1, the Ellison Medical

Foundation grant AG-NS-0724-10, Walter F. Heiligenberg Professorship, National Science Foundation Collaborative Research in Computational Neuroscience grant 1010463, and US National

Institutes of Health grants R21 MH100354 and R01 NS086947. AUTHOR INFORMATION Author notes * Magdalene I Schlesiger and Christopher C Cannova: These authors contributed equally to this work.

AUTHORS AND AFFILIATIONS * Neurobiology Section and Center for Neural Circuits and Behavior, University of California, San Diego, La Jolla, California, USA Magdalene I Schlesiger, 

Christopher C Cannova, Brittney L Boublil, Emily A Mankin, Mark P Brandon, Jill K Leutgeb & Stefan Leutgeb * Graduate School of Systemic Neurosciences, Ludwig-Maximilians-Universität

München, Planegg, Germany Magdalene I Schlesiger * Department of Psychiatry, School of Medicine, University of California, San Diego, La Jolla, California, USA Jena B Hales * Department

Biology II, Ludwig-Maximilians-Universität München, Planegg, Germany Christian Leibold * Kavli Institute for Brain and Mind, University of California, San Diego, La Jolla, California, USA

Stefan Leutgeb Authors * Magdalene I Schlesiger View author publications You can also search for this author inPubMed Google Scholar * Christopher C Cannova View author publications You can

also search for this author inPubMed Google Scholar * Brittney L Boublil View author publications You can also search for this author inPubMed Google Scholar * Jena B Hales View author

publications You can also search for this author inPubMed Google Scholar * Emily A Mankin View author publications You can also search for this author inPubMed Google Scholar * Mark P

Brandon View author publications You can also search for this author inPubMed Google Scholar * Jill K Leutgeb View author publications You can also search for this author inPubMed Google

Scholar * Christian Leibold View author publications You can also search for this author inPubMed Google Scholar * Stefan Leutgeb View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS M.I.S., S.L. and J.K.L. designed experiments, M.I.S., J.B.H. and S.L. performed surgeries, M.I.S. and B.L.B. acquired data, M.P.B. provided data,

C.C.C., M.I.S., J.B.H., E.A.M., C.L. and S.L. performed analysis, and M.I.S., C.C.C, J.K.L., C.L. and S.L. wrote the manuscript. CORRESPONDING AUTHOR Correspondence to Stefan Leutgeb. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. INTEGRATED SUPPLEMENTARY INFORMATION SUPPLEMENTARY FIGURE 1 SUFFICIENT LFP THETA POWER FOR PHASE AND

FREQUENCY ANALYSIS WAS RETAINED IN ALL RATS WITH LESIONS THAT INCLUDED THE ENTIRE EXTENT OF THE MEDIAL ENTORHINAL CORTEX. (A) (Top two rows) Photographs of NeuN-stained sections through the

medial entorhinal cortex (MEC) from a control rat and from an MEC-lesioned rat in which the lesion size was close to the group average. Three sagittal levels are shown for each rat (d,

dorsal; v, ventral; a, anterior; p, posterior). Red lines delineate MEC borders. Scale bars are 1 mm. (Bottom left) Average lesion size in different MEC layers. The percentage of damaged

tissue was quantified for each layer along the entire extent of MEC (including dorsal, intermediate and ventral MEC). Dots indicate lesion size in individual hemispheres, and matching colors

are from the same rat. Bars graphs, mean ± SEM. (Bottom right) Electrode tracks in the left and right dorsal hippocampus of two MEC-lesioned rats. Termination sites in the CA1 cell layer

are marked with arrows. Scale bars are 1 mm. (B,C) Example LFP traces (gray, raw signal; black, 4-12 Hz filtered) and 1/_f_ corrected spectrograms from the selected tetrode that was used for

phase and frequency analysis in the three control rats and in five MEC-lesioned rats with recordings on the linear track. An additional rat (Rat 587) with recordings from only 2 cells for

which no PSSFs were identified is not shown. Scale bars are 250 μV and 100 ms. Vertical lines indicate the peak of each LFP-theta cycle. SUPPLEMENTARY FIGURE 2 PERIODS OF STABLE SPATIAL

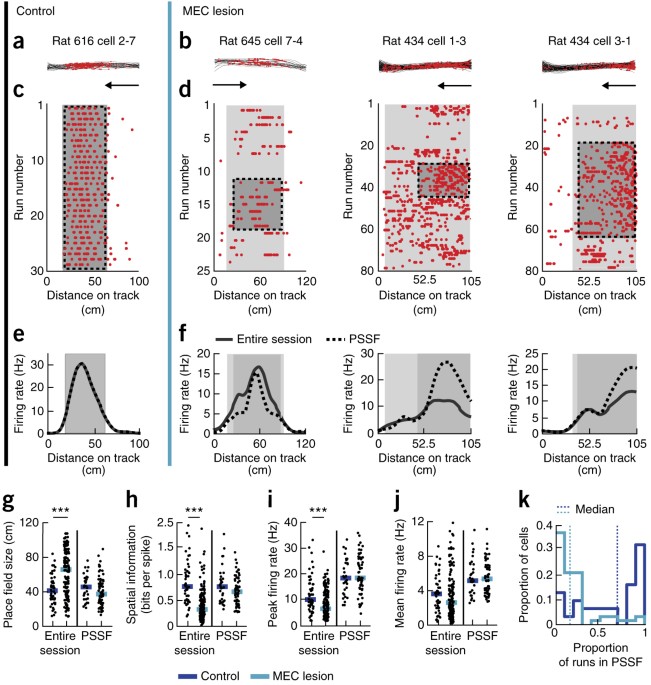
FIRING WERE SHORTER IN MEC-LESIONED THAN IN CONTROL RATS. Example place fields on the linear track from two control rats (A, rat 616 and rat 614) and from two MEC-lesioned rats (B, rat 645

and rat 434). Data recorded during the turn are not shown and were excluded from the analysis. Each column (from i to iii) depicts the spatial firing pattern of one cell during running in

one direction (indicated by the arrow). (i) Trajectories (black lines) and spike locations (red dots) within the place field. (ii) Raster plots with each row corresponding to a run from one

end of the track to the other. (iii) Firing rate versus distance on the linear track. Place field boundaries and firing rates are shown for the entire session (gray line and enclosed entire

shaded area) and for the period of stable spatial firing longest PSSF (PSSF; stippled line and enclosed, darker shaded gray area). SUPPLEMENTARY FIGURE 3 SINGLE‐UNIT RECORDINGS WERE STABLE

THROUGHOUT PERIODS WHEN THE SPATIAL FIRING PATTERNS IN MEC‐LESIONED RATS SHIFTED. (A,B) Recording quality and cluster stability are depicted for representative tetrodes from a control rat

(rat 616, black vertical line) and from an MEC‐lesioned rat (Rat 434, blue vertical line). (i) Scatter plots of spike amplitudes or spike energy (i.e., the area under the amplitude curve)

for two of the four recording channels of a tetrode. The first and second half of the recording session are shown separately. In each scatter plot, spikes are represented as dots. Because

spikes that are generated by individual cells tend to have consistent amplitude distributions across channels, spikes from the same cell form clusters within the scatter plots. Spikes

assigned to each cluster are shown in matching colors. Spikes that did not clearly separate into clusters were not included into the analysis and are shown in gray. Within each recording

session, clusters remained in a stable position in amplitude and energy space. (ii) Raster plots of spatial firing patterns with the spike locations (red dots) during each run in one

direction (black arrow) on the linear track. Periods of stable spatial firing (PSSFs) that were used for phase precession analysis are highlighted in gray. (iii) Spike amplitudes over the

course of a recording session are shown for the cells in the raster plots. Each tetrode channel is a different color. Cluster quality measures (L‐ratio and isolation distance) are noted for

each cell. Cells recorded from MEC‐lesioned rats did not show changes in spike amplitude beyond the small variability that was also observed in controls, and these cells thus showed stable

spike amplitudes even at time points when the spatial firing patterns shifted. (C) Comparison between the average spike amplitudes during the first and during second half of each recording.

The amplitude difference on the channel with the highest amplitude, the percent change on the channel with the highest amplitude, as well as the Euclidean distance between the amplitudes on

all four channels were calculated. None of these measurements showed differences between cells from control and cells from MEC‐lesioned rats (control, _n_ = 74 cells; MEC‐lesioned, _n_ = 163

cells with > 20 spikes; amplitude difference, _P_ = 0.39; percent change, _P_ = 0.23; Euclidean distance, _P_ = 0.51; Mann‐Whitney _U_ tests). (D,E) Cluster quality in control and

MEC-lesioned rats. The L‐ratio indicated a better cluster quality in cells from MEC‐lesioned compared to control rats (control, _n_ = 75 cells; MEC‐lesioned, _n_ = 170 cells with > 12

spikes; _P =_ 0.049, Mann‐Whitney _U_ test) while the isolation distance was significantly lower after the MEC lesion (_P =_ 0.040, Mann‐Whitney _U_ test). Along with these inconsistent

differences between the groups, the distributions showed substantial overlap. Together with lack of amplitude differences within the recording sessions (see C), we could therefore not find

any indication that the more frequent shifts in spatial firing patterns in the cells from MEC‐lesioned rats could be explained by differences in cluster stability or quality. SUPPLEMENTARY

FIGURE 4 PHASE PRECESSION IS SUBSTANTIALLY DISRUPTED IN ALL MEC-LESIONED RATS. Additional examples of spatial and temporal firing patterns on the linear track. Pooled and single pass phase

precession analysis from a control rat (A, rat 614) and two MEC-lesioned rats (B, rat 434 and rat 645). For each PSSF, the place field, LFP traces and spike trains are shown. (Top left of

each panel) Firing rate on the linear track (stippled line) with the extent of the field during the PSSF indicated by a shaded box. Arrows indicate the running direction. (Top right of each

panel) Firing phase versus relative distance in the field for all passes through the field. A regression line (black) is added when the circular-linear correlation was significant (_P_ <

0.05). For better visualization, the phase of each spike is replotted in a second cycle. (Lower panels in each box) For passes through the place field, the LFP trace (gray, raw signal;

black, 4-12 Hz filtered) and the spike times are depicted (red ticks). Black vertical lines indicate the peak of each LFP-theta cycle. Scale bars are 250 µV and 100 ms. To the right of the

trace for each pass, the corresponding firing phase of each spike is plotted as a function of the relative distance through the field. A regression line (black) is added when the

circular-linear correlation was significant (_P_ < 0.05). Analysis of pooled passes and single passes revealed a deficit of phase precession in cells from MEC-lesioned rats, while

prominent phase precession was observed in control cells. SUPPLEMENTARY FIGURE 5 MEC LESIONS RESULTED IN HIGHLY VARIABLE AND A LOWER PROPORTION OF SIGNIFICANT PHASE-DISTANCE CORRELATIONS

DURING SINGLE PASSES THROUGH HIPPOCAMPAL PLACE FIELDS. (A,B) Firing phase-distance regression slopes for single passes (blue ticks) through each field. Corresponding field-averaged slope

(black tick) and SEM (error bars) are shown on the horizontal axis. Fields are arranged from top to bottom by increasing field-averaged slope. All slopes (top) and only slopes where the

circular-linear correlation was significant (_P_ < 0.05) (bottom) are shown for control rats (left) and MEC-lesioned rats (right). (A) Single pass slopes and corresponding field-averages

for the entire recording session. (B) Same as in A for periods of stable spatial firing (PSSFs). (C) Slopes were first calculated for single passes through each field and then averaged per

field (_n_ = 47 control fields and 133 fields from MEC-lesioned rats). Insets: field-average of only significant slopes (_P_ < 0.05, circular-linear correlation; _n_ = 39 control fields

and 89 fields from MEC-lesioned rats). (D) Same as in C for PSSFs (see also Fig. 3; _n_ = 31 control fields and 50 fields from MEC-lesioned rats; only significant slopes: control, _n_ = 25

fields; MEC-lesioned, _n_ = 27 fields). Within each graph, the stippled orange line indicates the mean of the field-averaged slopes. Gray shading highlights the region of the graph where

slopes are negative. Compared to control rats, the CA1 cells from MEC-lesioned rats exhibited phase-distance slopes that were less frequently negative (entire recording session: 88.9 % for

control fields and 61.5 % for fields from MEC-lesioned rats, _P_ = 1.3 x 10−6, Mann-Whitney _U_ test; PSSFs: 88.9 % for control fields and 60.0 % for fields from MEC-lesioned rats, _P_ =

0.00020, Mann-Whitney _U_ test), less frequently significant (entire recording session: 40.0 % for control fields and 20.0 % for fields from MEC-lesioned rats, _P_ = 0.00019, Mann-Whitney

_U_ test; PSSFs: 50.0 % for control fields and 9.6 % for fields from MEC-lesioned rats, _P_ = 0.0045, Mann-Whitney _U_ test), and more variable (median standard deviation in entire recording

session: 0.35 for control fields and 0.91 for fields from MEC-lesioned rats, _P_ = 3.5 x 10−9, Mann-Whitney _U_ test; PSSFs: 0.22 for control fields and 0.87 for fields from MEC-lesioned

rats, _P_ = 0.0023, Mann-Whitney _U_ test) during single passes through their respective place fields. SUPPLEMENTARY FIGURE 6 SPATIAL AND TEMPORAL FIRING CHARACTERISTICS OF EXAMPLE PLACE

FIELDS RECORDED IN THE OPEN FIELD. All cells recorded on one representative tetrode per rat are shown for two control rats (A, black vertical line) and three MEC-lesioned rats (B, blue

vertical line). (First column of each cell’s panel) Color-coded rate maps (blue to red, 0 Hz to peak rate). Scale bars are 50 cm. (Second column) Corresponding trajectory plot with the rat’s

path (gray line) and the location of spikes (red dots). The place field boundaries are overlaid in black. (Third column) Spike-time autocorrelogram. (Fourth column) The phases of all

in-field spikes fired during the 10-min session are plotted as a function of the relative distance through the field. A regression line (black) is added when the circular-linear correlation

was significant (_P_ < 0.05, circular-linear correlation). Significant negative slopes, which indicate phase precession, are found for most fields from control rats (35/46, 76.1 %) but

only for few fields from MEC-lesioned rats (5/21, 23.8 %). SUPPLEMENTARY FIGURE 7 EXAMPLE PASSES THROUGH PLACE FIELDS IN THE OPEN FIELD. Pooled and single pass analysis for (A) a place cell

from a control rat and (B,C) two simultaneously recorded cells from an MEC-lesioned rat. (Top row of each panel, from left to right) Color-coded rate map (blue to red, 0 Hz to peak rate),

trajectory plot with the rat’s path (gray line) and the location of spikes (red dots), spike-time autocorrelogram, phase-distance plot for all in-field spikes fired during a 10-min session.

(Additional pairs of plots in each panel) Trajectory and phase-distance plots for all individual passes through the place field. The place field boundaries (black line) are overlaid on all

trajectory plots. A regression line is added to the phase-distance plots when significant (_P_ < 0.05, circular-linear correlation). SUPPLEMENTARY FIGURE 8 FIELD-AVERAGED SINGLE-PASS

ANALYSIS DURING SEPTAL INACTIVATION. Single trial phase precession was analyzed during a 10-minute session before and at two time points during septal inactivation. (A–C) Phase-distance

plots of example cells that were recorded before inactivation, 30 min into the inactivation, and 2 h into the inactivation. For each cell the phase-distance plot is shown for all passes

through the place field (pooled passes, left in each panel) as well as for one representative pass through the place field (single pass, right in each panel). For better visualization, the

phase of each spike is replotted in a second cycle. Regression lines (black) are added when the circular-linear correlation was significant (_P_ < 0.05). (D, top row) Representative

time-averaged and 1/f corrected spectrograms of LFP recordings used for theta phase analysis. (D, bottom row) Distributions of phase-distance slopes. For each cell, slopes were first

calculated for single passes through each field and then averaged per field (see Fig. 7 for the analysis of pooled passes). Insets: field-average of only significant slopes (_P_ < 0.05,

circular-linear correlation). (E, top) To calculate theta phase and frequency, a recording tetrode with theta power of at least 1.5 times over the 1/f baseline was chosen for each recording

session (_n_ = 5, one tetrode per session). Mean theta power on tetrodes selected for phase and frequency analysis. Dots indicate individual sessions, and matching colors are used for the

same tetrode. Mean theta power on selected tetrodes in the MEC-lesioned group is shown for comparison (blue line). (E, bottom) The mean field-averaged slope was less than zero before the

inactivation (all slopes, _n_ = 52, _P_ = 1.01 x 10−5, _t_ test; only significant slopes, _n_ = 45, _P_ = 9.33 x 10−9, sign test), not different from zero during the session 30 min into the

inactivation (all slopes, _n_ = 46, _P_ = 0.54, _t_ test; only significant slopes, _n_ = 30, _P_ = 0.86, sign test), and again less than zero during the session 2h into the inactivation (all

slopes, _n_ = 44, _P_ = 2.09 x 10−5, _t_ test; only significant slopes, _n_ = 32, _P_ = 0.020, sign test). The session at 30 min but not at 2 h into the inactivation was different from

baseline (_P_ = 0.00027 and _P_ = 0.22, Mann-Whitney _U_ test). The mean field-averaged slope in MEC-lesioned rats (all slopes, _n_ = 25) was different from baseline, but not different from

recordings in either of the septal inactivation sessions (_P_ = 0.028, _P_ = 0.97, _P_ = 0.13, Mann-Whitney _U_ test). Bar graphs include mean ± SEM. See Supplementary Table 4 for detailed

statistics. ***_P_ < 0.001, * _P_ < 0.05, compared to MEC lesion group. ### _P_ < 0.001, baseline compared to septal inactivation, Holm-Bonferroni corrected for multiple

comparisons. (F) Schematic of the relation between spikes (red ticks) and theta oscillations (black lines) with and without jitter. Vertical gray lines indicate the peak of each theta cycle.

(Top) Schematic of a spike train that exhibits clear phase precession over the course of three theta cycles. (Middle) Same spike train as shown on top after the application of spike-timing

jitter. Spike-timing jitter was simulated by adding zero-mean Gaussian noise with a particular standard deviation (σt) to each spike time prior to phase estimation. (bottom) Same spike train

as shown on top after the application of phase-onset jitter. Phase onset jitter was simulated by adding zero-mean Gaussian noise with a particular standard deviation (σϕ) to the phase of

all spikes within a theta-associated burst (TAB; see Online Methods). Single spikes not included in a TAB were treated analogously. (G) Phase-distance plots corresponding to spikes pooled

from all passes through the same field before and after applying the same jitter as shown in F. Note that, despite the ambiguity introduced at the level of single passes, the overall

phase-distance relationship over all passes remains largely unchanged after the application of a relatively large degree of jitter. (H) Phase-distance plots and corresponding circular-linear

regression lines obtained from two example passes through a place field (top) before jitter was applied, (middle) after the application of spike time jitter (σt = 20 ms), and (bottom) after

the application of phase onset jitter (σϕ = 15.00 % theta cycle). Each spike is replotted in a second cycle for clarity. Note the ambiguity introduced in the phase-distance relationship

after the application of jitter and its effect on the slope of the regression line. (I) Spike time (top) and phase onset (bottom) jitter were applied separately to the spikes of cells

recorded during baseline conditions, where clear phase precession was observed (see Fig. 7). Data without the application of jitter (Baseline) are represented at a standard deviation of

zero. All other symbols (circles) represents the average of 100 iterations (that is for each iteration, jitter applied to all fields) per degree of jitter (that isi.e., standard deviation on

horizontal axis). For each iteration, a _t_ test was used to test the means of the resulting field-averaged single pass (green lines) and pooled pass (purple lines) slope distributions

against zero at the α = 0.05 significance level. The shading of each circle corresponds to the proportion of trial distributions with mean values that were significantly different from zero

for each degree of jitter (white to black, 0 to 1). Note that the degree of jitter required to render phase precession undetectable (e.g. obtain an average distribution mean close to 0) is

lower for field-averaged single pass distributions than for pooled pass distributions, irrespective of the type of jitter simulated. Phase precession measures based on field-averaged single

pass slopes are thus less robust to jitter than slopes obtained by pooling spikes from all passes through a field. SUPPLEMENTARY FIGURE 9 SCHEMATIC MODEL OF CA1 INTRACELLULAR DYNAMICS THAT

REQUIRE MEC INPUTS FOR PHASE PRECESSION. Our results can be explained if we assume three input pathways (top three traces) combined at the CA1 pyramidal cell: the local theta oscillation

(Hippocampus), a non-oscillatory but spatially modulated input from the LEC, and an oscillatory and spatially modulated input induced by MEC. In the model, the MEC-induced oscillator is

assumed to be faster than the local oscillator (gray and white bars), which reflects our finding that cellular oscillations are slower in the MEC-lesioned rats. Mechanistically this could be

explained by resonance properties in the dendrites, as described in ref. 50. A weighted linear superposition of the three inputs yields a membrane potential that comprises both ramp like

and oscillatory character and an additional increase in the oscillation amplitude as reported in ref. 28. Setting a constant action potential threshold (red) defines a distinct

space-dependent phase range (blue) during which the cell may fire. In the control case with all three inputs intact (left column) the mean of the phase range decreases with space. In the

MEC-lesioned case (right column) the mean of the phase range stays stationary. The width of the place field, however, is not substantially affected be the absence of MEC input. SUPPLEMENTARY

INFORMATION SUPPLEMENTARY TEXT AND FIGURES Supplementary Figures 1–9 and Supplementary Tables 1–4 (PDF 11404 kb) SOURCE DATA SOURCE DATA TO FIG. 1 SOURCE DATA TO FIG. 2 SOURCE DATA TO FIG.

3 SOURCE DATA TO FIG. 4 SOURCE DATA TO FIG. 5 SOURCE DATA TO FIG. 6 SOURCE DATA TO FIG. 7 SOURCE DATA TO FIG. 8 RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Schlesiger, M., Cannova, C., Boublil, B. _et al._ The medial entorhinal cortex is necessary for temporal organization of hippocampal neuronal activity. _Nat Neurosci_ 18, 1123–1132

(2015). https://doi.org/10.1038/nn.4056 Download citation * Received: 19 January 2015 * Accepted: 04 June 2015 * Published: 29 June 2015 * Issue Date: August 2015 * DOI:

https://doi.org/10.1038/nn.4056 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently

available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative