Experimental investigation of classical and quantum correlations under decoherence

ABSTRACT It is well known that many operations in quantum information processing depend largely on a special kind of quantum correlation, that is, entanglement. However, there are also

quantum tasks that display the quantum advantage without entanglement. Distinguishing classical and quantum correlations in quantum systems is therefore of both fundamental and practical

importance. In consideration of the unavoidable interaction between correlated systems and the environment, understanding the dynamics of correlations would stimulate great interest. In this

study, we investigate the dynamics of different kinds of bipartite correlations in an all-optical experimental setup. The sudden change in behaviour in the decay rates of correlations and

their immunity against certain decoherences are shown. Moreover, quantum correlation is observed to be larger than classical correlation, which disproves the early conjecture that classical

correlation is always greater than quantum correlation. Our observations may be important for quantum information processing. You have full access to this article via your institution.

Download PDF SIMILAR CONTENT BEING VIEWED BY OTHERS AN INHERENTLY INFINITE-DIMENSIONAL QUANTUM CORRELATION Article Open access 03 July 2020 MULTIPARTITE ENTANGLEMENT ANALYSIS FROM RANDOM

CORRELATIONS Article Open access 09 June 2020 ENTANGLEMENT-ASSISTED QUANTUM COMMUNICATION WITH SIMPLE MEASUREMENTS Article Open access 22 December 2022 INTRODUCTION Correlations, including

classical and quantum parts, are crucial in science and technology. Although many operations in quantum information processing depend largely on a special kind of quantum correlation, that

is, entanglement1, there are quantum tasks that display the quantum advantage without entanglement2,3,4, and some of these have been verified experimentally5. Distinguishing classical and

quantum correlations is therefore of both fundamental and practical importance. Many theoretical studies have been conducted in this direction6,7,8,9,10,11,12,13,14. Among them, quantifying

the quantumness of correlations with quantum discord7 has received great attention4,5,15,16,17,18,19,20,21,22,23,24,25,26. In the field of quantum information, for a bipartite system

_ρ__AB_, it is widely accepted that quantum mutual information measures its total correlations12,27 defined as _I_(_ρ__AB_)=_S_(_ρ__A_)+_S_(_ρ__B_)−_S_(_ρ__AB_)28, where _ρ__A_ and _ρ__B_

are the reduced-density matrices of _ρ__AB_. _S_(_ρ_)=−tr_ρ_log2_ρ_ in the von Neumann entropy. Depending on the maximal information gained for _ρ__AB_ with measurement on one of the

subsystems, classical correlation (_C_)6 is defined as _C_(_ρ__AB_)≡ max B j † B j [_S_(ρA)-σ_j__q__j__S_(ρjA)], where _B__j_†_B__j_ is a positive-operator-valued measure performed on the

subsystem _B_ and _q__j_=tr_AB_(_B__j__ρ__AB__B__j__†_). ρAj=trB(BjρABBj†)/_q__j_ is the postmeasurement state of _A_ after obtaining outcome _j_ on particle _B_. Quantum correlation is

therefore given by _Q_(_ρ__AB_)=_I_(_ρ__AB_)−_C_(_ρ__AB_). In such a case, _Q_ is just identical to quantum discord with a definition based on the distinction between classical information

theory and quantum information theory7, which can be further distributed into entanglement and the additional quantum correlation (non-entanglement quantum correlation)29. Because of the

unavoidable interaction between a quantum system and its environment, understanding the dynamics of different kinds of correlations has stimulated great interest. Some studies have focused

on the comparison between the dynamics of quantum discord and entanglement under both Markovian19 and non-Markovian21,22 environments. Their behaviours have been shown to be very different,

and the quantum discord is more robust against decoherence than entanglement in the Markovian evolution19. Recently, several peculiar properties in the dynamics of classical and quantum

correlations have also been shown with the presence of Markovian noise23,24, in which the decay rates of correlations may exhibit sudden changes in behaviour23 and the bipartite quantum

correlation may completely disappear without being transferred to the environment24. In this study, we experimentally investigate the dynamics of classical and quantum correlations between

biqubit systems in a one-sided phase-damping channel. The sudden changes in behaviours in the decay rates of classical and quantum correlations are shown in an all-optical experimental

setup, in which the dephasing environment is simulated by birefringent quartz plates. Classical and quantum correlations are observed to remain unaffected under certain decoherence areas.

Moreover, quantum correlation is shown to be larger than classical correlation during the dynamics of a special input state, which contradicts the early conjecture that classical correlation

is always greater than quantum correlation30. Our observations may have important roles in quantum information processing. RESULTS THEORETICAL SCHEMES Consider a two-level quantum system

_S_ with lower and upper states |0〉_S_ and |1〉_S_ under the action of a phase-damping environment _E_(|0〉_E_ is the initial state). The interaction quantum map can be written as31 Under such

a uniquely quantum mechanical noise process, the system _S_ remains in the initial state with the probability _p_ of scattering the environment to its excited state |1〉_E_, if _S_ is in

state |0〉_S_, and to |2〉_E_, if _S_ is in state |1〉_S_. It physically describes, for instance, the case when a photon scatters randomly in a fibre. The coherence of _S_ degrades

exponentially, and _p_=1−exp(−Γ_t_), where Γ is the decay rate. When it extends to the case of bipartite systems coupling with this environment, the decoherence-free states32 and the

phenomenon of entanglement collapse and revival33 have been shown. When an initial Bell-diagonal state , with and representing the four Bell states and _a_+_b_+_c_+_d_=1 evolves in the

phase-damping channel given by equation (1), its off-diagonal elements decay exponentially according to the previous analysis. Because _S_(_ρ__A_)=_S_(_ρ__B_)=1, the total correlation is

calculated as where λ_j_ are the four eigenvalues of the final density matrix. To calculate the classical correlation6, the state in mode _B_ is projected into |_l_〉=cos_θ|0_〉+sin_θe__iφ_|1〉

to get the minimal conditional entropy of subsystem _A_, where 0≤_θ_≤π and 0≤_φ_≤2_π_. In the biqubit case, the projective measurement is the positive-operator-valued measure to maximize

_C_(_ρ__AB_)34, which is expressed as23 represents the conditional entropy of _A_ with projecting _B_ in |_l_〉 and _η_=max{|_α_|,|_β_|,|_γ_|} with _α_=(1−_p_)(_a_−_b_+_c_−_d_),

_β_=(1−_p_)(_c_−_d_−_a_+_b_) and _γ_=_a_+_b_−_c_−_d_. The quantum correlation is therefore given by EXPERIMENTAL DEMONSTRATION OF THE DYNAMICS OF CORRELATIONS Photon qubits with polarization

encoded as the information carriers have been widely used to implement different quantum information processing procedures1. The coupling between photon polarization and frequency modes in

a birefringent environment leads to dephase by a trace-over frequency35, which simulates the decoherence effect in equation (1). Here, we encode the horizontal (_H_) and vertical (_V_)

polarizations of a photon as |0〉_S_ and |1〉_S_ of a qubit and pass the polarization-entangled photons through one-sided controllable quartz plates to investigate the dynamics of different

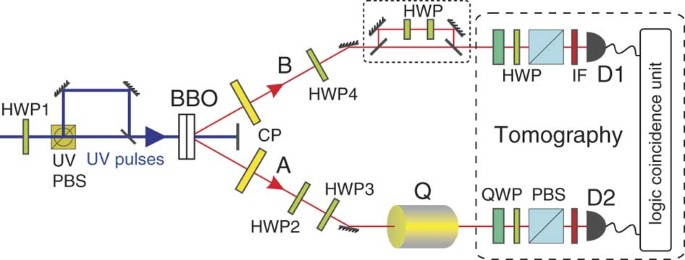
kinds of correlations. Figure 1 shows our experimental setup. Ultraviolet pulses are frequency doubled from a mode-locked Ti:sapphire laser with wavelength centred at 780 nm, with a 130 fs

pulse width and a 76 MHz repetition rate. They are distributed into two paths by an ultraviolet polarization beam splitter, which transmits 45° linearly polarized photons () and reflects

−45° linearly polarized photons (). The relative power between these two paths can be changed easily by a half-wave plate (HWP1), and the time difference between them is about 6 ns. They

then combine again by a beam splitter, and both pump two identically cut type-I β-barium borate crystals, with their optic axes aligned in mutually perpendicular planes, to produce

polarization-entangled photon pairs36. After compensating the birefringence effect between _H_ and _V_ with quartz plates (CP), the short pump beam produces the maximally entangled state

|φ+〉, whereas the long pump beam produces |φ−〉. Two HWPs (HWP2 and HWP4), with the optic axes set to 22.5°, can change _H_ into and _V_ into . The HWP (HWP3) with the optic axis set as

horizontal in mode _A_ is used to introduce the _π_-phase between _H_ and _V_. As our detection traces over the time difference between these two production processes, as has been shown

earlier37,38, the prepared state becomes where _b_ is determined by the relative power between these two pump beams and _b_+_d_=1. Thereafter, the photon in mode _A_ with frequency

distribution _f_(_ω_) passes through the dephasing channel, which is simulated by quartz plates (_Q_), with the optic axis set to be horizontal and with a thickness of _L_. Therefore, the

decoherence parameter imposes on the off-diagonal elements of equation (5), where _τ_=_L_Δ_n_/_c_, with _c_ representing the vacuum velocity of the photon and Δ_n_ is the difference between

the indices of refraction of _H_ and _V_. In this case, we obtain _p_=1−|_κ_| in equation (1). An unbalanced Mach–Zehnder device in the dotted pane, which further separates the photon into

long and short paths, is inserted into mode _B_ to prepare another input state. The long path in the dotted pane contains a HWP with the optic axis set at 45° and another HWP with the optic

axis set as horizontal. The time difference between these two paths is much larger than the coherent time of the photon and less than the coincidence window of the logic circuit (at about 3

ns). As a result, the prepared state becomes where _R_ is the effective total reflectivity of the two partial reflecting mirrors in the dotted pane. The photon in mode _A_ then further

passes through the dephasing channel. Finally, the evolved state is reconstructed by tomography. Quarter-wave plates, HWPs and polarization beam splitters are used in each mode to set the

usual 16 measurement bases39. These two photons are detected by single-photon detectors equipped with 3 nm (full width at half maximum) interference filters. Figure 2 shows the correlation

dynamics of input state (5) with _b_=0.75 in the phase-damping channel. Theoretically, the minimum of conditional entropy _S_(ρlA) in mode _A_ is obtained by projecting the photon in mode

_B_ onto |_l_〉=cos_θ_|_H_〉+sin_θe__iφ_|_V_〉, with optimization over the angles _θ_ and _φ_. In our experiment, we measured _S_(ρlA) as a function of _θ_ with _φ=0_ in different thicknesses

of quartz plates, as shown in Fig. 2a. We found that the minimum value of _S_(ρlA) is obtained with _θ_=45° at about _L_<138_λ_0 and _θ_=0° at about _L_≥138λ0 (_λ_0=0.78 _μ_m is the

central wavelength of the photon), which agree well with theoretical predictions (solid lines)23. This implies that there is a sudden change in behaviour in the decay rate of _C_ according

to equation (3). The dynamics of total correlation (_I_), classical correlation (_C_) and quantum correlation (_Q_) are shown in Fig. 2b. We find that _C_ (black squares) decays

monotonically at _L_<138λ0 and then remains constant at _L_≥138_λ_0, which agrees with Fig. 2a. Such immunity of classical correlation against decoherence implies an operational way to

compute classical and quantum correlations23. In contrast, _Q_ (red dots) behaves in the opposite manner; it remains constant at _L_<138_λ_0 and decays monotonically at _L_≥138_λ_0. _C_

and _Q_ overlap at the specific thickness of about _L_=138_λ_0. It is interesting to observe the 'decoherence-free' area of quantum correlation, which is due to the equal decay

rate of _I_ and _C_. This phenomenon is later shown explicitly in theory by Mazzola _et al_.40. It may have important applications for those quantum information protocols using only quantum

correlation. We can see that _I_ (green upward-pointing triangles) decays exponentially all the time, which is consistent with the continuous dynamics of quantum mutual information according

to equation (2). The green solid line, black solid line and red dashed line are the corresponding theoretical predictions of the total, classical and quantum correlations. Error bars

correspond to counting statistics. The dynamics of entanglement is also shown in Fig. 2b, which is characterized by both the entanglement of formation (En)41 and the relative entropy of

entanglement (Rn)42 (the analytical expressions of both characterizations in our case are given in Methods). The blue stars in Fig. 2b are the experimental results of En and the blue dotted

line is the corresponding theoretical prediction. The value of entanglement is set to 0 at a thickness of about _L_=173_λ_0, which shows the phenomenon of entanglement sudden death43,

whereas the magenta downward-pointing triangles are the experimental results of Rn. Because the final state in our experiment can be transformed into a Bell-diagonal form, with a local

unitary operation that does not change its entanglement, the analytical expressions of Rn (see Methods) are used to give the theoretical prediction, which is represented by the magenta

dotted line. Although the En is larger than the relative Rn at the beginning of evolution, they suffer from sudden death at the same thickness, thereby confirming their self-consistence. We

can see that quantum correlation can be smaller or larger than the En during evolution. Specifically, quantum correlation decays exponentially, whereas entanglement disappears completely at

the thickness of _L_>173_λ_0. This confirms the earlier prediction that quantum discord is more robust against decoherence than entanglement19,20. Because the relative Rn is on an equal

footing with other measures of correlations in the form of entropy29, it is not always larger than quantum correlation, as verified by our experimental results. The inset in Fig. 2b further

compares non-entanglement quantum correlation defined as _D_=_Q_−Rn29 with classical correlation. Purple dots are the experimental results of _D_, with the purple dotted line representing

theoretical prediction. Because of the sudden change in behaviour of _Q_, the decay rate of _D_ also suffers from sudden changes and we find that _D_<_C_. Another kind of correlation

dynamics is shown in Fig. 3, in which the sudden change behaviour disappears. The input state is given by equation (5) with _b_=0.5 (the separated state, Fig. 3, top panel) and _b_=1 (the

maximally entangled state, Fig. 3, bottom panel). The minimum of _S_(ρlA) is obtained with _θ_=45° in Fig. 3 (top panel) and _θ_=0° in Fig. 3 (bottom panel) (_φ_=0)23. The green

upward-pointing triangles, black squares and red dots represent the experimental results of _I_, _C_ and _Q_, respectively. The quantum correlation in Fig. 3 (top panel) remains at 0 and the

total correlation is equal to the classical correlation, both of which decay monotonically. Figure 3 (bottom panel) shows another case in which classical correlation remains at 1 and

quantum correlation decays exponentially. Compared with the dynamics of entanglement En (blue stars), we find that entanglement also remains at 0, as shown in Fig. 3 (top panel)

(experimental results not shown), which is equal to _Q_ there, whereas it is larger than the _Q_ during evolution, as shown in Fig. 3 (bottom panel). Orange diamonds represent the value of Λ

(if Λ ≥ 0, it represents the quantity of concurrence44; see Methods), which also decays exponentially. The value of En is set to 0 when Λ<0 according to its definition. The relative Rn

(magenta downward-pointing triangles) is also shown in Fig. 3. It remains constant at 0, as shown in Fig. 3 (top panel) (experimental results not shown) and then decays exponentially, as

shown in Fig. 3 (bottom panel). Rn completely overlaps with quantum correlation in both cases, and the non-entanglement quantum correlation reads at 0. The experimental results agree well

with the corresponding theoretical predictions. We further show an interesting case in which _Q_ can be larger than _C_. In this case, the dotted pane is inserted into mode _B_, as shown in

Fig. 1 and the initial input state is given by equation (6). We set _b_=0.9 and _R_=0.9 to maximize the value of _Q_−_C_. Fig. 4 shows our experimental results. The total correlation (green

upward-pointing triangles) decays exponentially, whereas the classical (black squares) and quantum (red dots) correlations exhibit sudden changes in behaviour in their decay rates at about

_L_=78λ0. After this special thickness, the classical correlation remains constant and the quantum correlation decays exponentially with a higher decay rate. During evolution, _Q_ is

observed to be larger than _C_ at the thickness interval from about 50_λ_0 to 90_λ_0, within the error bars. Such an observation contradicts the early conjecture that _C_ ≥ _Q_30, and is

consistent with previous theoretical predictions23,25,26. The dynamics of entanglement, which are characterized by both En (blue stars) and Rn (magenta downward-pointing triangles), are also

shown in Fig. 4. Both characterizations suffer from sudden death at the same thickness of about _L_=202λ0, and the entanglement is set to 0 in the subsequent evolution. The value of the

non-entanglement quantum correlation _D_ (purple dots), which also exhibits a sudden change in the decay rate, is compared with the classical correlation in the inset. We find that

entanglement and non-entanglement quantum correlations are always less than the classical correlation in our experiment. DISCUSSION The classical and quantum correlations considered in this

experiment are defined by the one-partition measurement of a bipartite system6,7. In such cases, analytical solutions for classical and quantum correlations have been obtained for some kinds

of states with a high symmetry18,23,25. Although classical and quantum correlations may be generally asymmetric according to the choice of partition to be measured, for states with

maximally mixed marginals, they are symmetric under the interchange of the measured side24. There is also a quantifier of classical correlation with measurement over both partitions of a

bipartite system, which is defined as the maximum classical mutual information9,10. For states with maximally mixed marginals, the definitions of classical and quantum correlations are

numerically verified to be equal to that defined with one-sided measurement24. A thermodynamic approach is also developed to quantify correlations8,11. In particular, the quantum information

deficit is defined to characterize the difference between the information that can be localized with Closed Local Operations and Classical Communications and the total information of the

state, and it quantifies the quantumness of correlations11. We find that the quantum-information deficit is equal to quantum discord for Bell-diagonal states. On the basis of the idea that

classical states can be measured without disturbance, Luo13 uses the measurement-induced disturbance to characterize classical and quantum correlations. Because of the symmetric property of

Bell-diagonal states, these definitions of correlations used in our experiment also coincide with that defined by Luo's method14. Recently, a method to quantify quantum and classical

correlations on an equal footing with relative entropy has been proposed14, and it is applicable to multiparticle systems of arbitrary dimensions. In our case, considering the dynamics of

Bell-diagonal states, the one-sided definitions of classical and quantum correlations6,7 are consistent with those defined by the equal footing method14. As a result, for the Bell-diagonal

states used in our experiment, all of the above separation methods for classical and quantum correlations are coincident. Through measuring classical and quantum correlations in multipartite

systems, Bennett _et al_.45 recently introduced three postulates that should be satisfied by any measure or indicator of genuine multipartite correlations. They found that the concept of

covariance proposed by Kaszlikowski _et al_.46 to identify the existence of genuine multipartite correlations does not satisfy two postulates, and they concluded that it cannot be an

indicator of genuine multipartite classical correlations45. Because the equal footing method mentioned above can be directly applied to multipartite systems with a unified view of quantum

and classical correlations14, it may inspire insight into current debates. The relationship between the En and quantum correlation is also interesting. In our experiment, the En is observed

to be even larger than quantum correlation in certain areas of evolution. For bipartite systems, it has also been shown that quantum mutual information considered as the measurement of total

correlation can be smaller than the En47,48, which may occur in the case of particles with dimensions larger than five48. Such a contradiction is due to the different frameworks of their

definitions. In our case, we can choose the relative Rn to measure entanglement, so as to make it on an equal footing with other measures of correlations in the form of entropy29. In

conclusion, we have shown the sudden change in behaviour in the decay rates of different kinds of correlations in the two-photon system. Our results show that classical and quantum

correlations can remain unaffected under certain decoherence areas, which will have important roles in distinguishing correlations23 and designing robust quantum protocols based only on

quantum correlation. The early conjecture that _C_≥_Q_30 is disproved by our experimental results. On the other hand, classical correlation is always found to be larger than the entanglement

and non-entanglement quantum correlation in the experiment. METHODS ANALYTICAL EXPRESSIONS OF THE EN AND THE RELATIVE RN For biqubit systems, the En can be given by the analytical formula44

where _H_(_x_)=−_x_log2_x_−(1−_x_)log2(1−_x_), ϒ is the concurrence given by ϒ=max{0, Λ}, where and _X__j_ are the eigenvalues in decreasing order of the matrix

_ρ_(_σ_2⊗_σ_2)_ρ_*(_σ_2⊗_σ_2), with _σ_2 denoting the second Pauli matrix and _ρ_* corresponding to the complex conjugate of _ρ_ in the canonical basis {|_HH_〉,|_HV_〉,|_VH_〉,|_VV_〉}. In

addition, the relative Rn is defined as the minimal distance between _ρ_ and a disentangled state42. For the Bell-diagonal state, if the four eigenvalues of the density matrix are , the

relative Rn is given by42 ,whereas for any _λ__j_≥1/2, we obtain ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Li, C.-F. _et al_. Experimental investigation of classical and quantum

correlations under decoherence. _Nat. Commun._ 1:7 doi: 10.1038/ncomms1005 (2010). REFERENCES * Nielsen, M. A. & Chuang, I. L. _Quantum Computation and Quantum Information_ (Cambridge

University Press, 2000). * Meyer, D. A. Sophisticated quantum search without entanglement. _Phys. Rev. Lett._ 85, 2014–2017 (2000). Article  ADS  CAS  Google Scholar  * Kenigsberg, D., Mor,

T. & Ratsaby, G. Quantum advantage without entanglement. _Quantum Inf. Comput._ 6, 606–615 (2006). MathSciNet  MATH  Google Scholar  * Datta, A., Shaji, A. & Caves, C. M. Quantum

discord and the power of one qubit. _Phys. Rev. Lett._ 100, 050502 (2008). Article  ADS  Google Scholar  * Lanyon, B. P., Barbieri, M., Almeida, M. P. & White, A. G. Experimental quantum

computing without entanglement. _Phys. Rev. Lett._ 101, 200501 (2008). Article  ADS  CAS  Google Scholar  * Henderson, L. & Vedral, V. Classical, quantum and total correlations. _J.

Phys. A Math. Gen._ 34, 6899–6905 (2001). Article  ADS  MathSciNet  Google Scholar  * Ollivier, H. & Zurek, W. H. Quantum discord: a measure of the quantumness of correlations. _Phys.

Rev. Lett._ 88, 017901 (2001). Article  ADS  Google Scholar  * Oppenheim, J., Horodecki, M., Horodecki, P. & Horodecki, R. Thermodynamical approach to quantifying quantum correlations.

_Phys. Rev. Lett._ 89, 180402 (2002). Article  ADS  Google Scholar  * Terhal, B. M., Horodecki, M., Leung, D. W. & DiVincenzo, D. P. The entanglement of purification. _J. Math. Phys._

43, 4286–4298 (2002). Article  ADS  MathSciNet  CAS  Google Scholar  * DiVincenzo, D. P., Horodecki, M., Leung, D. W., Smolin, J. A. & Terhal, B. M. Locking classical correlations in

quantum states. _Phys. Rev. Lett._ 92, 067902 (2004). Article  ADS  Google Scholar  * Horodecki, M. et al. Local versus nonlocal information in quantum-information theory: formalism and

phenomena. _Phys. Rev. A_ 71, 062307 (2005). Article  ADS  Google Scholar  * Groisman, B., Popescu, S. & Winter, A. Quantum, classical, and total amount of correlations in a quantum

state. _Phys. Rev. A_ 72, 032317 (2005). Article  ADS  MathSciNet  Google Scholar  * Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum.

_Phys. Rev. A_ 77, 022301 (2008). Article  ADS  Google Scholar  * Modi, K., Paterek, T., Son, W., Vedral, V. & Williamson, M. Unified view of quantum and classical correlations. _Phys.

Rev. Lett._ 104, 080501 (2010). Article  ADS  MathSciNet  Google Scholar  * Zurek, W. H. Quantum discord and Maxwell's demons. _Phys. Rev. A_ 67, 012320 (2003). Article  ADS  Google

Scholar  * Rodríguez-Rosario, C. A., Modi, K., Kuah, A. M., Shaji, A. & Sudarshan, E .C. G. Completely positive maps and classical correlations. _J. Phys. A Math. Theor._ 41, 205301

(2008). Article  ADS  MathSciNet  Google Scholar  * Piani, M., Horodecki, P. & Horodecki, R. No-local-broadcasting theorem for multipartite quantum correlations. _Phys. Rev. Lett._ 100,

090502 (2008). Article  ADS  Google Scholar  * Luo, S. Quantum discord for two-qubit systems. _Phys. Rev. A_ 77, 042303 (2008). Article  ADS  Google Scholar  * Werlang, T., Souza, S.,

Fanchini, F. F. & Boas, C. J. V. Robustness of quantum discord to sudden death. _Phys. Rev. A_ 80, 024103 (2009). Article  ADS  Google Scholar  * Ferraro, A., Aolita, L., Cavalcanti, D.,

Cucchietti, F. M. & Acin, A. Almost all quantum states have non-classical correlations. Preprint at 〈http://arxiv.org/abs/0908.3157v2〉 ( 2009). * Wang, B., Xu, Z. -Y., Chen, Z. -Q.

& Feng, M. Non-Markovian effect on the quantum discord. _Phys. Rev. A_ 81, 014101 (2010). Article  ADS  Google Scholar  * Fanchini, F. F., Werlang, T., Brasil, C. A., Arruda, L. G. E.

& Caldeira, A. O. Non-Markovian dynamics of quantum discord. Preprint at 〈http://arxiv.org/abs/0911.1096v3〉 ( 2009). * Maziero, J., Céleri, C. L., Serra, R. M. & Vedral, V. Classical

and quantum correlations under decoherence. _Phys. Rev. A_ 80, 044102 (2009). Article  ADS  MathSciNet  Google Scholar  * Maziero, J., Werlang, T., Fanchini, F. F., Céleri, C. L. &

Serra, R. M. System-reservoir dynamics of quantum and classical correlations. _Phys. Rev. A_ 81, 022116 (2010). Article  ADS  Google Scholar  * Sarandy, M. S. Classical correlation and

quantum discord in critical systems. _Phys. Rev. A_ 80, 022108 (2009). Article  ADS  Google Scholar  * Luo, S. & Zhang, Q. Observable correlations in two-qubit states. _J. Stat. Phys._

136, 165–177 (2009). Article  ADS  MathSciNet  CAS  Google Scholar  * Schumacher, B. & Westmoreland, M. D. Quantum mutual information and the one-time pad. _Phys. Rev. A_ 74, 042305

(2006). Article  ADS  Google Scholar  * Vedral, V. The role of relative entropy in quantum information theory. _Rev. Mod. Phys._ 74, 197–234 (2002). Article  ADS  MathSciNet  Google Scholar

  * Vedral, V. The elusive source of quantum effectiveness. Preprint at 〈http://arxiv.org/abs/0906.3656v1〉 (2009). * Lindblad, G. Quantum entropy and quantum measurement. In _Quantum Aspects

of Optical Communications. Lecture Notes in Physics_ Vol 378 (eds. Bendjaballah, C., et al.) 71–80 (Springer, 1991). * Preskill, J. Lecture notes quantum information and computation,

http://www.theory.caltech.edu/people/preskill/ph229/notes/chap3.pdf (1998). * Kwiat, P. G., Berglund, A. J., Altepeter, J. B. & White, A. G. Experimental verification of decoherence-free

subspaces. _Science_ 290, 498–501 (2000). Article  ADS  CAS  Google Scholar  * Xu, J. -S. et al. Experimental demonstration of photonic entanglement collapse and revival. _Phys. Rev. Lett._

104, 100502 (2010). Article  ADS  Google Scholar  * Hamieh, S., Kobes, R. & Zaraket, H. Positive-operator-valued measure optimization of classical correlations. _Phys. Rev. A_ 70,

052325 (2004). Article  ADS  Google Scholar  * Berglund, A. J. Quantum coherence and control in one- and two-photon optical systems. Preprint at 〈http://arxiv.org/abs/quant-ph/0010001v2〉 (

2000). * Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. _Phys. Rev. A_ 60, R773–R776 (1999). Article  ADS 

CAS  Google Scholar  * Puentes, G., Voigt, D., Aiello, A. & Woerdman, J. P. Tunable spatial decoherers for polarization-entangled photons. _Opt. Lett._ 31, 2057–2059 (2006). Article  ADS

  Google Scholar  * Aiello, A., Puentes, G., Voigt, D. & Woerdman, J. P. Maximally entangled mixed-state generation via local operations. _Phys. Rev. A_ 75, 062118 (2007). Article  ADS 

MathSciNet  Google Scholar  * James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. _Phys. Rev. A_ 64, 052312 (2001). Article  ADS  Google Scholar  * Mazzola,

L., Piilo, J. & Maniscalco, S. Sudden transition between classical and quantum decoherence. Preprint at 〈http://arxiv.org/abs/1001.5441v2〉 ( 2010). * Bennett, C. H., DiVincenzo, D. P.,

Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. _Phys. Rev. A_ 54, 3824–3851 (1996). Article  ADS  MathSciNet  CAS  Google Scholar  * Vedral, V.,

Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying entanglement. _Phys. Rev. Lett._ 78, 2275–2279 (1997). Article  ADS  MathSciNet  CAS  Google Scholar  * Yu, T. & Eberly, J.

H. Sudden death of entanglement. _Science_ 323, 598–601 (2009). Article  ADS  MathSciNet  CAS  Google Scholar  * Wootters, W. K. Entanglement of formation of an arbitrary state of two

qubits. _Phys. Rev. Lett._ 80, 2245–2248 (1998). Article  ADS  CAS  Google Scholar  * Bennett, C. H., Grudka, A., Horodecki, M., Horodecki, P. & Horodecki, R. Postulates for measures of

genuine multipartite correlations. Preprint at 〈http://arxiv.org/abs/0805.3060v2〉 ( 2010). * Kaszlikowski, D., Sen(De), A., Sen, U., Vedral, V. & Winter, A. Quantum correlation without

classical correlations. _Phys. Rev. Lett._ 101, 070502 (2008). Article  ADS  Google Scholar  * Hayden, P., Leung, D. W. & Winter, A. Aspects of generic entanglement. _Commun. Math.

Phys._ 265, 95–117 (2006). Article  ADS  MathSciNet  Google Scholar  * Li, N. & Luo, S. Total versus quantum correlations in quantum states. _Phys. Rev. A_ 76, 032327 (2007). Article 

ADS  Google Scholar  Download references ACKNOWLEDGEMENTS We thank V. Vedral, S. Luo and Y.-C. Wu for helpful discussions. This work was supported by the National Fundamental Research

Program, the National Natural Science Foundation of China (Grant No. 60121503, 10874162). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Key Laboratory of Quantum Information, University of

Science and Technology of China, CAS, Hefei 230026, China Jin-Shi Xu, Xiao-Ye Xu, Chuan-Feng Li, Cheng-Jie Zhang, Xu-Bo Zou & Guang-Can Guo Authors * Jin-Shi Xu View author publications

You can also search for this author inPubMed Google Scholar * Xiao-Ye Xu View author publications You can also search for this author inPubMed Google Scholar * Chuan-Feng Li View author

publications You can also search for this author inPubMed Google Scholar * Cheng-Jie Zhang View author publications You can also search for this author inPubMed Google Scholar * Xu-Bo Zou

View author publications You can also search for this author inPubMed Google Scholar * Guang-Can Guo View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS C.F.L. and J.S.X. designed the experiment. J.S.X. and X.Y.X. performed the experiment. J.S.X. analysed the theoretical prediction and experimental data. C.J.Z., X.B.Z. and

G.C.G. contributed to the theoretical analysis. J.S.X. and C.F.L. wrote the paper. CORRESPONDING AUTHORS Correspondence to Chuan-Feng Li or Xu-Bo Zou. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing financial interests. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Xu, JS., Xu, XY., Li, CF. _et al._ Experimental

investigation of classical and quantum correlations under decoherence. _Nat Commun_ 1, 7 (2010). https://doi.org/10.1038/ncomms1005 Download citation * Received: 12 February 2010 * Accepted:

03 March 2010 * Published: 12 April 2010 * DOI: https://doi.org/10.1038/ncomms1005 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative